Deck 11: Statistical Inferences Based on Two Samples
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/140
العب
ملء الشاشة (f)
Deck 11: Statistical Inferences Based on Two Samples
1
In an experiment involving matched pairs, a sample of 12 pairs of observations is collected. The degrees of freedom for the t statistic is 10.
False
2
In testing the difference between two population variances, it is a common practice to compute the F statistic so that its value is always greater than or equal to one.
True
3
There are two types of machines, called type A and type B. Both type A and type B can be used to produce a certain product. The production manager wants to compare efficiency of the two machines. He assigns each of the 15 workers to both types of machines to compare their hourly production rate. In other words, each worker operates machine A and machine B for one hour each. These two samples are independent.
False
4
In testing the difference between the means of two normally distributed populations using large independent random samples, the sample sizes from the two populations must be equal.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
5
In testing the difference between two means from two independent populations, the sample sizes do not have to be equal.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
6
If the limits of the confidence interval of the difference between the means of two normally distributed populations were from −2.6 to 1.4 at the 95 percent confidence level, then we can conclude that we are 95 percent certain that there is a significant difference between the two population means.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
7
The controller of a chain of toy stores is interested in determining whether there is any difference in the weekly sales of store 1 and store 2. The weekly sales are normally distributed. This problem should be analyzed using an independent means method.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
8
In forming a confidence interval for μ1 − μ2, only two assumptions are required: independent samples and sample sizes of at least 30.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
9
In testing the equality of population variances, two assumptions are required: independent samples and normally distributed populations.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
10
When testing the difference between two proportions selected from populations with large independent samples, the z test statistic is used.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
11
When comparing two population means based on independent random samples, the pooled estimate of the variance is used when there is an assumption of equal population variances.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
12
Assume that we are constructing a confidence interval for the difference in the means of two populations based on independent random samples. If both sample sizes n1 and n2 =10, and the distributions of both populations are highly skewed, then a confidence interval for the difference in the means can be constructed using the t test statistic.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
13
If the limits of the confidence interval of the difference between the means of two normally distributed populations were 8.5 and 11.5 at the 95 percent confidence level, then we can conclude that we are 95 percent certain that there is a significant difference between the two population means.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
14
When comparing the variances of two normally distributed populations using independent random samples, if s12 = s12, the calculated value of F will always be equal to one.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
15
When we are testing a hypothesis about the difference in two population proportions based on large independent samples, we compute a combined (pooled) proportion from the two samples if we assume that there is no difference between the two proportions in our null hypothesis.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
16
In testing the difference between the means of two normally distributed populations using independent random samples, the alternative hypothesis always indicates no difference between the two specified means.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
17
When comparing two independent population means, if n1 = 13 and n2 = 10, degrees of freedom for the t statistic is 22.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
18
In testing the difference between the means of two normally distributed populations using independent random samples, we can only use a two-sided test.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
19
In testing the difference between the means of two independent populations, if neither population is normally distributed, then the sampling distribution of the difference in means will be approximately normal, provided that the sum of the sample sizes obtained from the two populations is at least 30.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
20
An independent samples experiment is an experiment in which there is no relationship between the measurements in the different samples.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
21
In testing the difference between the means of two normally distributed populations using independent random samples with equal variances, the correct test statistic to use is the
A) z statistic.
B) t statistic.
C) F statistic.
D) chi-square statistic.
E) None of the other choices is correct.
A) z statistic.
B) t statistic.
C) F statistic.
D) chi-square statistic.
E) None of the other choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
22
In order to test the effectiveness of a drug called XZR designed to reduce cholesterol levels, the cholesterol levels of 9 heart patients are measured before they are given the drug. The same 9 patients use XZR for two continuous months. After two months of continuous use, the cholesterol levels are measured again. The comparison of cholesterol levels before versus after administering the drug is an example of testing the difference between
A) two means from independent populations.
B) two population variances from independent populations.
C) two population proportions.
D) matched pairs from two dependent populations.
A) two means from independent populations.
B) two population variances from independent populations.
C) two population proportions.
D) matched pairs from two dependent populations.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
23
The F statistic can assume either a positive or a negative value.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
24
A new company is in the process of evaluating its customer service. The company offers two types of sales: (1) Internet sales and (2) store sales. The marketing research manager believes that the Internet sales are more than 10 percent higher than store sales. The null hypothesis would be
A) PInternet − Pstore > .10.
B) PInternet − Pstore < .10.
C) PInternet − Pstore ≥ .10.
D) PInternet − Pstore ≤ .10.
E) PInternet − Pstore = .10.
A) PInternet − Pstore > .10.
B) PInternet − Pstore < .10.
C) PInternet − Pstore ≥ .10.
D) PInternet − Pstore ≤ .10.
E) PInternet − Pstore = .10.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
25
A new company is in the process of evaluating its customer service. The company offers two types of sales: (1) Internet sales and (2) store sales. The marketing research manager believes that the Internet sales are more than 10 percent higher than store sales. The alternative hypothesis for this problem would be stated as
A) PInternet − Pstore > 0.
B) PInternet − Pstore < 0.
C) PInternet − Pstore ≥ .10.
D) PInternet − Pstore ≤ .10.
E) PInternet − Pstore > .10.
A) PInternet − Pstore > 0.
B) PInternet − Pstore < 0.
C) PInternet − Pstore ≥ .10.
D) PInternet − Pstore ≤ .10.
E) PInternet − Pstore > .10.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
26
When comparing two independent population means by using samples selected from two independent, normally distributed populations with equal variances, the correct test statistic to use is ________.
A) z
B) t
C) F
D) t2
A) z
B) t
C) F
D) t2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
27
A financial analyst working for a financial consulting company wishes to find evidence that the average price-to-earnings ratio in the consumer industry is higher than the average price-to-earnings ratio in the banking industry. The alternative hypothesis is
A) μconsumer = μbanking.
B) μconsumer ≤ μbanking.
C) μconsumer > μbanking.
D) μconsumer < μbanking.
E) μconsumer ≠ μbanking.
A) μconsumer = μbanking.
B) μconsumer ≤ μbanking.
C) μconsumer > μbanking.
D) μconsumer < μbanking.
E) μconsumer ≠ μbanking.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
28
When testing a hypothesis about the mean of a population of paired differences in which two different observations are taken on the same units, the correct test statistic to use is ________.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
29
In testing the difference between two means from two normally distributed independent populations, the distribution of the difference in sample means will be
A) normally distributed only if sample sizes are equal.
B) normally distributed only if both population standard deviations are known.
C) normally distributed.
D) normally distributed if both sample sizes are very large.
E) normally distributed only if both population variances are equal.
A) normally distributed only if sample sizes are equal.
B) normally distributed only if both population standard deviations are known.
C) normally distributed.
D) normally distributed if both sample sizes are very large.
E) normally distributed only if both population variances are equal.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
30
The value of Fα in a particular situation depends on the size of the right-hand tail area and the numerator degrees of freedom.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
31
The exact shape of the curve of the F distribution depends on two parameters, df1 and df2.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
32
If we are testing the difference between the means of two normally distributed independent populations with samples of n1 = 10, n2 = 10, the degrees of freedom for the t statistic is ________.
A) 19
B) 18
C) 9
D) 8
E) 20
A) 19
B) 18
C) 9
D) 8
E) 20

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
33
An experiment in which two different measurements are taken on the same units and inferences are made using the differences between the pairs of measurements is a(n) ________ experiment.
A) paired difference
B) equal variances
C) independent samples
D) dependent samples
A) paired difference
B) equal variances
C) independent samples
D) dependent samples

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
34
When testing the difference between two population proportions using large independent random samples, the ________ test statistic is used.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
35
Given the following information about a hypothesis test of the difference between two means based on independent random samples, which one of the following is the correct rejection region at a significance level of .05? HA: μA > μB, 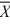 1 = 12,
1 = 12, 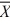 2 = 9, s1 = 4, s2 = 2, n1 = 13, n2 = 10.
2 = 9, s1 = 4, s2 = 2, n1 = 13, n2 = 10.
A) Reject H0 if t > 1.96.
B) Reject H0 if t > 1.645.
C) Reject H0 if t > 1.721.
D) Reject H0 if t > 2.08.
E) Reject H0 if t > 1.782.
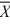 1 = 12,
1 = 12, 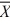 2 = 9, s1 = 4, s2 = 2, n1 = 13, n2 = 10.
2 = 9, s1 = 4, s2 = 2, n1 = 13, n2 = 10.A) Reject H0 if t > 1.96.
B) Reject H0 if t > 1.645.
C) Reject H0 if t > 1.721.
D) Reject H0 if t > 2.08.
E) Reject H0 if t > 1.782.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
36
When testing the difference between two population proportions, the ________ test statistic is used.
A) z
B) t
C) F
D) t2
A) z
B) t
C) F
D) t2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
37
In testing for the equality of means from two independent populations, if the hypothesis of equal population means is rejected at α = .01, it will ________ be rejected at α = .05.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
38
In which of the following tests is the variable of interest the difference between the values of the observations from the two samples, rather than the actual observations themselves?
A) a test of hypothesis about the mean of a population of paired differences selected from two related samples
B) a test of hypothesis about the difference between the means of two normally distributed populations using independent samples
C) a test of hypothesis about the difference between two population proportions, using large independent random samples
D) a test of hypothesis about the difference between the variances of two normally distributed populations using independent samples
A) a test of hypothesis about the mean of a population of paired differences selected from two related samples
B) a test of hypothesis about the difference between the means of two normally distributed populations using independent samples
C) a test of hypothesis about the difference between two population proportions, using large independent random samples
D) a test of hypothesis about the difference between the variances of two normally distributed populations using independent samples

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
39
An experiment in which there is no relationship between the measurements on the different samples is a(n) ________ experiment.
A) paired difference
B) equal variances
C) independent samples
D) dependent samples
A) paired difference
B) equal variances
C) independent samples
D) dependent samples

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
40
If we are testing the hypothesis about the mean of a population of paired differences with samples of n1 = 10, n2 = 10, the degrees of freedom for the t statistic is ________.
A) 19
B) 18
C) 9
D) 8
E) 10
A) 19
B) 18
C) 9
D) 8
E) 10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
41
Two independent samples selected from two normally distributed populations have variances of σ12 and σ22 with n1 = 10 and n2 = 15. The degrees of freedom for the F distribution when testing the equality of the two population variances are
A) 10 and 15.
B) 11 and 16.
C) 9 and 14.
D) 8 and 13.
A) 10 and 15.
B) 11 and 16.
C) 9 and 14.
D) 8 and 13.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
42
Given the following information about a hypothesis test of the difference between two means based on independent random samples, what is the standard deviation of the difference between the two means? Assume that the samples are obtained from normally distributed populations having equal variances. HA: μA > μB, 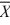 1 = 12,
1 = 12, 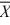 2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
A) 1.792
B) 1.679
C) 2.823
D) 3.210
E) 1.478
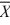 1 = 12,
1 = 12, 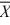 2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.A) 1.792
B) 1.679
C) 2.823
D) 3.210
E) 1.478

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
43
In comparing the difference between two independent population means, the sampling distributions of the population means are at least approximately ________.
A) skewed right
B) skewed left
C) normal
D) binomial
A) skewed right
B) skewed left
C) normal
D) binomial

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
44
Construct a 95 percent confidence interval for μ1 − μ2, where 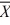 1 = 34.36,
1 = 34.36,  2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)
2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)
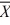 1 = 34.36,
1 = 34.36,  2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)
2 = 26.45, s1 = 9, s2 = 6, n1 = 10, n2 = 16. (Assume equal population variances.)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
45
If we are testing the hypothesis about the mean of a population of paired differences with samples of n1 = 8, n2 = 8, the degrees of freedom for the t statistic is ________.
A) 16
B) 7
C) 14
D) 9
A) 16
B) 7
C) 14
D) 9

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
46
When comparing the variances of two normally distributed populations using independent random samples, the correct test statistic to use is ________.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.
A) z
B) t
C) F
D) chi-square
E) None of the other choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
47
In testing the difference between two independent population means, if the assumption is of unequal variances, the critical value of the t statistic is obtained by calculating the ________.
A) degrees of freedom
B) sum of the two sample sizes (n1 + n2)
C) p-value
D) pooled variance
A) degrees of freedom
B) sum of the two sample sizes (n1 + n2)
C) p-value
D) pooled variance

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
48
When comparing two independent population variances, the correct test statistic to use is ________.
A) z
B) t
C) F
D) t 2
A) z
B) t
C) F
D) t 2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
49
Given the following information about a hypothesis test of the difference between two means based on independent random samples, what is the calculated value of the test statistic? Assume that the samples are obtained from normally distributed populations having equal variances. HA: μA > μB, 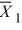 = 12,
= 12, 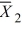 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
= 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
A) t = 1.96
B) t = 1.5
C) t = 2.823
D) t = 1.674
E) t = 1.063
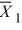 = 12,
= 12, 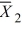 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
= 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.A) t = 1.96
B) t = 1.5
C) t = 2.823
D) t = 1.674
E) t = 1.063

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
50
In testing the difference between the means of two independent populations, the variances of the two samples can be pooled if the population variances are assumed to ________.
A) be unequal
B) be greater than the mean
C) sum to 1
D) be equal
A) be unequal
B) be greater than the mean
C) sum to 1
D) be equal

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
51
The test of means for two related populations matches the observations (matched pairs) in order to reduce the ________ attributable to the difference between individual observations and other factors.
A) means
B) test statistic
C) degrees of freedom
D) variation
A) means
B) test statistic
C) degrees of freedom
D) variation

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
52
When testing the difference for the population of paired differences in which two different observations are taken on the same units, the correct test statistic to use is ________.
A) z
B) t
C) F
D) t2
A) z
B) t
C) F
D) t2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
53
Given the following information about a hypothesis, and the test of the difference between two variances based on independent random samples, what is the critical value of the test statistic at a significance level of 0.05? Assume that the samples are obtained from normally distributed populations. HA: σ2A > σ2B, 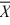 1 = 12,
1 = 12, 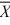 2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
A) 3.87
B) 2.67
C) 3.07
D) 2.80
E) 2.38
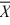 1 = 12,
1 = 12, 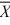 2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.
2 = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.A) 3.87
B) 2.67
C) 3.07
D) 2.80
E) 2.38

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
54
In testing the equality of population variance, what assumption(s) should be considered?
A) independent samples
B) equal sample sizes
C) normal distribution of the populations
D) independent samples and equal sample sizes
E) independent samples and normal distribution of the populations
A) independent samples
B) equal sample sizes
C) normal distribution of the populations
D) independent samples and equal sample sizes
E) independent samples and normal distribution of the populations

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
55
In testing the difference between the means of two normally distributed populations, if μ1 = μ2 = 50, n1 = 9, and n2 = 13, the degrees of freedom for the t statistic equals ________.
A) 22
B) 21
C) 19
D) 20
A) 22
B) 21
C) 19
D) 20

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
56
Parameters of the F distribution include
A) n1.
B) degrees of freedom for the numerator and the denominator.
C) n2.
D) n1 and n2.
E) None of the other choices is correct.
A) n1.
B) degrees of freedom for the numerator and the denominator.
C) n2.
D) n1 and n2.
E) None of the other choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
57
In testing the difference between two independent population means, it is assumed that the level of measurement is ________.
A) a ratio variable
B) a qualitative variable
C) an interval variable
D) a categorical variable
A) a ratio variable
B) a qualitative variable
C) an interval variable
D) a categorical variable

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
58
Given two independent normal distributions with s12 − s22= 100, μ1 = μ2 = 50, and n1 = n2 = 50, the sampling distribution of the mean difference 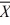 1 −
1 − 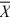 2 will have a mean of ________.
2 will have a mean of ________.
A) 100
B) 1
C) 0
D) 50
E) 10
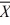 1 −
1 − 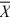 2 will have a mean of ________.
2 will have a mean of ________.A) 100
B) 1
C) 0
D) 50
E) 10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
59
In general, the shape of the F distribution is ________.
A) skewed right
B) skewed left
C) normal
D) binomial
A) skewed right
B) skewed left
C) normal
D) binomial

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
60
In order to test the effectiveness of a drug called XZR designed to reduce cholesterol levels, the cholesterol levels of 9 heart patients are measured before they are given the drug. The same 9 patients use XZR for two continuous months. After two months of continuous use, the cholesterol levels are measured again. The comparison of cholesterol levels before versus after the administration of the drug is an example of testing the difference between two ________.
A) samples of equal variances
B) independent samples
C) paired samples
D) samples of unequal variances
A) samples of equal variances
B) independent samples
C) paired samples
D) samples of unequal variances

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
61
Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where ![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://d2lvgg3v3hfg70.cloudfront.net/TB7056/11ead627_0a6a_04a5_93a1_a51f84bf3e94_TB7056_11.jpg) = 05,
= 05, ![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://d2lvgg3v3hfg70.cloudfront.net/TB7056/11ead627_0a6a_04a6_93a1_5172b9fa233e_TB7056_11.jpg) = .24, n1 = 500, and
= .24, n1 = 500, and
n2 = 2000, can we reject the null hypothesis at α = .10?
![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://d2lvgg3v3hfg70.cloudfront.net/TB7056/11ead627_0a6a_04a5_93a1_a51f84bf3e94_TB7056_11.jpg) = 05,
= 05, ![Using a 90 percent confidence interval of [−.0076, .0276] for the difference between the proportions of failures in factory 1 and factory 2, where = 05, = .24, n<sub>1</sub> = 500, and n<sub>2</sub> = 2000, can we reject the null hypothesis at α = .10?](https://d2lvgg3v3hfg70.cloudfront.net/TB7056/11ead627_0a6a_04a6_93a1_5172b9fa233e_TB7056_11.jpg) = .24, n1 = 500, and
= .24, n1 = 500, andn2 = 2000, can we reject the null hypothesis at α = .10?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
62
When we test H0: μ1 ≤ μ2, HA: μ1 > μ2 at α = .10, where 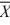 1 = 77.4,
1 = 77.4, 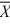 2 = 72.2, s1 = 3.3,
2 = 72.2, s1 = 3.3,
s2 = 2.1, n1 = 6, and n2 = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.)
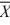 1 = 77.4,
1 = 77.4, 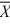 2 = 72.2, s1 = 3.3,
2 = 72.2, s1 = 3.3,s2 = 2.1, n1 = 6, and n2 = 6, can we reject the null hypothesis (using critical value rules)? (Assume equal variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
63
When we test H0: p1 − p2 ≤ .01, HA: p1 − p2 > .01, at α = .05, where  = .08,
= .08, 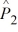 = .035,
= .035,
n1 = 200, and n2= 400, what is the standard deviation used to calculate the test statistic?
 = .08,
= .08, 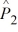 = .035,
= .035,n1 = 200, and n2= 400, what is the standard deviation used to calculate the test statistic?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
64
We are testing the hypothesis that the proportion of winter-quarter profit growth is more than 2 percent greater for consumer industry companies (CON) than for banking companies (BKG). At α = .10, given that 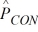 = .20,
= .20,  = .14, nCON = 300, and nBKG = 400, can we reject the null hypothesis (using critical value rules)?
= .14, nCON = 300, and nBKG = 400, can we reject the null hypothesis (using critical value rules)?
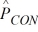 = .20,
= .20,  = .14, nCON = 300, and nBKG = 400, can we reject the null hypothesis (using critical value rules)?
= .14, nCON = 300, and nBKG = 400, can we reject the null hypothesis (using critical value rules)?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
65
Find a 90 percent confidence interval for the difference between the proportions of failures in factory 1 and factory 2, where 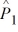 = .05,
= .05, 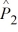 = .04, n1 = 500, and n2 = 2000.
= .04, n1 = 500, and n2 = 2000.
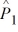 = .05,
= .05, 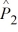 = .04, n1 = 500, and n2 = 2000.
= .04, n1 = 500, and n2 = 2000.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
66
When testing H0: μ1 − μ2 = 2, HA: μ1 − μ2 > 2, where 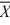 1 = 522,
1 = 522, 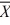 2 = 516, σ12 = 28,
2 = 516, σ12 = 28,
σ22 = 24, n1 = 40, n2 = 30, at α = .01, what is the test statistic? (Assume unequal variances.)
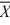 1 = 522,
1 = 522, 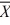 2 = 516, σ12 = 28,
2 = 516, σ12 = 28,σ22 = 24, n1 = 40, n2 = 30, at α = .01, what is the test statistic? (Assume unequal variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
67
Find a 95 percent confidence interval for the difference between means, where n1 = 50,
n2 = 36,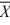 1 = 80,
1 = 80, 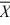 2 = 75, s12 = 5, and s22 = 3. Assume unequal variances.
2 = 75, s12 = 5, and s22 = 3. Assume unequal variances.
n2 = 36,
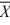 1 = 80,
1 = 80, 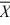 2 = 75, s12 = 5, and s22 = 3. Assume unequal variances.
2 = 75, s12 = 5, and s22 = 3. Assume unequal variances.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
68
Find a 95 percent confidence interval for the difference between the proportions of older and younger drivers who have tickets, where 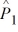 = .275,
= .275, 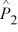 = .25, n1 = 1000, and n2 = 1000.
= .25, n1 = 1000, and n2 = 1000.
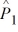 = .275,
= .275, 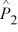 = .25, n1 = 1000, and n2 = 1000.
= .25, n1 = 1000, and n2 = 1000.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
69
When we test H0: μ1 − μ2 ≤ 0, HA: μ1 − μ2 > 0, 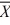 1 = 15.4,
1 = 15.4,  2 = 14.5, σ1 = 2, σ2 = 2.28,
2 = 14.5, σ1 = 2, σ2 = 2.28,
n1 = 35, and n2 = 18 at α = .01, what is the value of the test statistic?
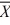 1 = 15.4,
1 = 15.4,  2 = 14.5, σ1 = 2, σ2 = 2.28,
2 = 14.5, σ1 = 2, σ2 = 2.28,n1 = 35, and n2 = 18 at α = .01, what is the value of the test statistic?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
70
We are testing the hypothesis that the proportion of winter-quarter profit growth is more than 2 percent greater for consumer industry companies (CON) than for banking companies (BKG). At α = .10, given that 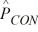 = .20,
= .20, 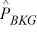 = .14, nCON = 300, and nBKG = 400, calculate the estimated standard deviation for the model.
= .14, nCON = 300, and nBKG = 400, calculate the estimated standard deviation for the model.
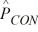 = .20,
= .20, 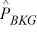 = .14, nCON = 300, and nBKG = 400, calculate the estimated standard deviation for the model.
= .14, nCON = 300, and nBKG = 400, calculate the estimated standard deviation for the model.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
71
When we test H0: μ1 − μ2 ≤ 0, HA: μ1 − μ2 > 0, 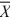 1 = 15.4,
1 = 15.4, 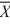 2 = 14.5, s1 = 2, s2 = 2.28,
2 = 14.5, s1 = 2, s2 = 2.28,
n1 = 35, and n2 = 18 at α = .01, can we reject the null hypothesis? (Assume unequal variances.)
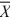 1 = 15.4,
1 = 15.4, 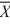 2 = 14.5, s1 = 2, s2 = 2.28,
2 = 14.5, s1 = 2, s2 = 2.28,n1 = 35, and n2 = 18 at α = .01, can we reject the null hypothesis? (Assume unequal variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
72
When we test H0: p1 − p2 ≤ .01, HA: p1 − p2 > .01 at α = .05 where 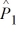 = .08,
= .08, 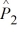 = .035,
= .035,
n1 = 200, and n2 = 400, can we reject the null hypothesis?
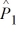 = .08,
= .08, 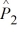 = .035,
= .035,n1 = 200, and n2 = 400, can we reject the null hypothesis?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
73
When we test H0: μ1 ≤ μ2, HA: μ1 > μ2 at α = .10, where 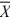 1 = 77.4,
1 = 77.4, 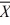 2 = 72.2, s1 = 3.3,
2 = 72.2, s1 = 3.3,
s2 = 2.1, n1 = 6, and n2 = 6, what is the estimated pooled variance?
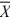 1 = 77.4,
1 = 77.4, 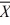 2 = 72.2, s1 = 3.3,
2 = 72.2, s1 = 3.3,s2 = 2.1, n1 = 6, and n2 = 6, what is the estimated pooled variance?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
74
Find a 98 percent confidence interval for the paired difference d1 − d2 where 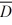 = 1.6, Sd 2= 40.96, n = 30
= 1.6, Sd 2= 40.96, n = 30
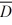 = 1.6, Sd 2= 40.96, n = 30
= 1.6, Sd 2= 40.96, n = 30
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find a 95 percent confidence interval for μ1 − μ2, where n1 = 50, n2 = 75,  1 = 82,
1 = 82, 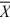 2 = 76, s12 = 8, and s22 = 6. Assume unequal variances.
2 = 76, s12 = 8, and s22 = 6. Assume unequal variances.
 1 = 82,
1 = 82, 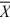 2 = 76, s12 = 8, and s22 = 6. Assume unequal variances.
2 = 76, s12 = 8, and s22 = 6. Assume unequal variances.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
76
Find a 90 percent confidence interval for the difference between the proportions of group 1 and group 2. Let p1 represent the population proportion of the people in group 1 who like a new mobile app, and let p2 represent the population proportion of the people in group 2 who like a new mobile app. 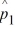 = .21,
= .21,  = .13, n1 = 300, and n2 = 400.
= .13, n1 = 300, and n2 = 400.
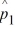 = .21,
= .21,  = .13, n1 = 300, and n2 = 400.
= .13, n1 = 300, and n2 = 400.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
77
Sample 1 has data: 16, 14, 19, 18, 19, 20, 15, 18, 17, 18; and sample 2 has data: 13, 19, 14, 17, 21, 14, 15, 10, 13, 15. Testing the equality of means at α = .05, can we reject the null hypothesis (using critical value rules)? (Assume equal population variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
78
When testing H0: μ1 − μ2 = 2, HA: μ1 − μ2 > 2, where 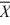 1 = 522,
1 = 522, 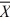 2 = 516, s12 = 28, s22 = 24, n1 = 40, n2 = 30, at α = .01, what can we conclude using critical value rules? (Assume unequal variances.)
2 = 516, s12 = 28, s22 = 24, n1 = 40, n2 = 30, at α = .01, what can we conclude using critical value rules? (Assume unequal variances.)
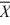 1 = 522,
1 = 522, 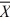 2 = 516, s12 = 28, s22 = 24, n1 = 40, n2 = 30, at α = .01, what can we conclude using critical value rules? (Assume unequal variances.)
2 = 516, s12 = 28, s22 = 24, n1 = 40, n2 = 30, at α = .01, what can we conclude using critical value rules? (Assume unequal variances.)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
79
Find a 95 percent confidence interval for μ1 − μ2, where n1 = 15, n2 = 10, 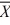 1 = 1.94,
1 = 1.94,
2 = 1.04, s12 = .2025, and s22 = .0676. (Assume equal population variances.)
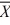 1 = 1.94,
1 = 1.94,2 = 1.04, s12 = .2025, and s22 = .0676. (Assume equal population variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck
80
Find a 95 percent confidence interval for μ1 − μ2, where n1 = 9, n2 = 6, 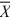 1 = 64,
1 = 64, 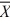 2 = 59,
2 = 59,
s12 = 6, and s22 = 3. (Assume equal population variances.)
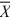 1 = 64,
1 = 64, 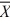 2 = 59,
2 = 59,s12 = 6, and s22 = 3. (Assume equal population variances.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 140 في هذه المجموعة.
فتح الحزمة
k this deck








