Deck 8: Nonlinear Programming and Evolutionary Optimization
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/68
العب
ملء الشاشة (f)
Deck 8: Nonlinear Programming and Evolutionary Optimization
1
The optimal solution to a LP problem is always at I.a cormer point.
II.an interior point
III. the origin
A) I is true
B) II is true
C) III is true
D) I and III are true
II.an interior point
III. the origin
A) I is true
B) II is true
C) III is true
D) I and III are true
I is true
2
The optimal solution to a NLP problem can occur at a(n) I.cormer paint.
II.interior point
A) I is true
B) II is true
C) I and II are true
D) neither I or II is true
II.interior point
A) I is true
B) II is true
C) I and II are true
D) neither I or II is true
I and II are true
3
The Risk Solver Platform (RSP) solution strategy for NLP problems is the GRG method. What does GRG stand for?
A) Graphical Residual Gradient
B) Generalized Reduced Gradient
C) Goal Restricted Gradient
D) Gradually Reduced Gradient
A) Graphical Residual Gradient
B) Generalized Reduced Gradient
C) Goal Restricted Gradient
D) Gradually Reduced Gradient
B
4
The GRG algorithm terminates when it
A) has completed 100 iterations.
B) has reached the global optimal solution.
C) when it detects no feasible direction for improvement.
D) when it reaches the steepest gradient.
A) has completed 100 iterations.
B) has reached the global optimal solution.
C) when it detects no feasible direction for improvement.
D) when it reaches the steepest gradient.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
5
The total annual cost for the economic order quantity model is
A) purchase cost + ordering cost + holding cost.
B) fixed ordering cost + holding cost.
C) purchase cost + fixed ordering cost.
D) unit cost + variable ordering cost + holding cost.
A) purchase cost + ordering cost + holding cost.
B) fixed ordering cost + holding cost.
C) purchase cost + fixed ordering cost.
D) unit cost + variable ordering cost + holding cost.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
6
The GRG algorithm operates by
A) moving in the direction of most rapid improvement in the objective function.
B) choosing a search direction at random.
C) searching directly for the optimum solution.
D) moving in a clockwise direction.
A) moving in the direction of most rapid improvement in the objective function.
B) choosing a search direction at random.
C) searching directly for the optimum solution.
D) moving in a clockwise direction.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
7
The main difference between LP and NLP problems is that NLPs will have a
A) linear objective function and nonlinear or linear constraints.
B) minimum of one nonlinear constraint or a nonlinear objective function.
C) multilevel objective functions.
D) multilevel objective function and nonlinear constraints.
A) linear objective function and nonlinear or linear constraints.
B) minimum of one nonlinear constraint or a nonlinear objective function.
C) multilevel objective functions.
D) multilevel objective function and nonlinear constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
8
NLP problems which have slack in all the constraints
A) are infeasible.
B) are only at local optimal solutions.
C) have zeros for all shadow prices.
D) are at an interior point of the feasible region.
A) are infeasible.
B) are only at local optimal solutions.
C) have zeros for all shadow prices.
D) are at an interior point of the feasible region.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
9
If the "Standard LP/Quadratic Engine" option is chosen in the Risk Solver Platform (RSP) task pane, RSP
A) will test for non-linearity in the model and apply GRG.
B) will test for non-linearity in the model and apply Simplex.
C) uses the B & B algorithm to solve the problem.
D) will apply Simplex if the linearity test passes.
A) will test for non-linearity in the model and apply GRG.
B) will test for non-linearity in the model and apply Simplex.
C) uses the B & B algorithm to solve the problem.
D) will apply Simplex if the linearity test passes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
10
What is the search path for the following feasible solution space? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 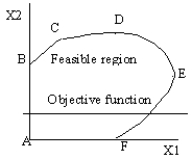
A) A, D
B) A, F, E, D
C) A, B, C, D
D) A, F, E

A) A, D
B) A, F, E, D
C) A, B, C, D
D) A, F, E

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
11
When using the GRG algorithm to solve NLPs one should try multiple starting points because
A) If two different starting points return the same solution, that solution is optimal.
B) the solution returned depends upon the starting point.
C) the solution returned is always near the starting point.
D) a random element of GRG requires multiple starting points.
A) If two different starting points return the same solution, that solution is optimal.
B) the solution returned depends upon the starting point.
C) the solution returned is always near the starting point.
D) a random element of GRG requires multiple starting points.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
12
The straight line (Euclidean) distance between two points (X1, Y1) and (X2, Y2) is calculated as
A) X1 ? Y1 + X2 ? Y2
B) (X1 ? X2)2 + (Y1 ? Y2)2
C)
D)
A) X1 ? Y1 + X2 ? Y2
B) (X1 ? X2)2 + (Y1 ? Y2)2
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
13
What is the straight line (Euclidean) distance between the points (5,7) and (1, 11)?
A) 2.83
B) 5.65
C) 8
D) 16
A) 2.83
B) 5.65
C) 8
D) 16

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
14
In NLP a local optimum is best described as
A) an interior point.
B) a corner point.
C) a point yielding no improving direction.
D) a good starting point for subsequent searches.
A) an interior point.
B) a corner point.
C) a point yielding no improving direction.
D) a good starting point for subsequent searches.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
15
The GRG and Simplex algorithms are similar in that
A) each algorithm process continues until there is no further improvement in the objective function.
B) both algorithms take their starting solution from the spreadsheet.
C) both return the globally optimal solution.
D) both algorithms return a solution that satisfies at least one constraint at equality.
A) each algorithm process continues until there is no further improvement in the objective function.
B) both algorithms take their starting solution from the spreadsheet.
C) both return the globally optimal solution.
D) both algorithms return a solution that satisfies at least one constraint at equality.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
16
The optimal trade-off between risk and return for a given portfolio problem can be summarized by the
A) efficient frontier.
B) investment frontier.
C) portfolio boundary.
D) variance boundary.
A) efficient frontier.
B) investment frontier.
C) portfolio boundary.
D) variance boundary.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
17
In the GRG algorithm the initial solution is called the
A) originating point.
B) insertion point.
C) zero point.
D) starting point.
A) originating point.
B) insertion point.
C) zero point.
D) starting point.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
18
Which point or points are global optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 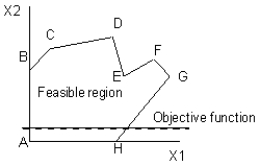
A) B
B) D
C) E
D) F

A) B
B) D
C) E
D) F

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
19
In a maximization problem, the GRG algorithm's search for a feasible direction of improvement equates to ____ in the simplex algorithm for LP problems.
A) an adjacent corner point
B) a zero reduced cost
C) a positive shadow price
D) a positive reduced cost
A) an adjacent corner point
B) a zero reduced cost
C) a positive shadow price
D) a positive reduced cost

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
20
Which point or points are local optima in this diagram? The dashed line represents the objective function and the objective is to maximize the value of the objective function. 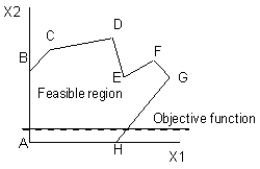
A) D
B) E
C) F
D) D, F

A) D
B) E
C) F
D) D, F

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
21
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formula goes in cell D4 of the spreadsheet? 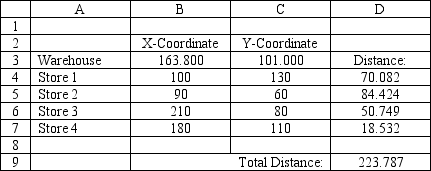
A) =(B4-$B$3)^2+(C4-$C$3)^2
B) =SQRT((B4-$B$3)+(C4-$C$3))
C) =SQRT((B4-$B$3)^2+(C4-$C$3)^2)
D) =(B4-$B$3)+(C4-$C$3)

A) =(B4-$B$3)^2+(C4-$C$3)^2
B) =SQRT((B4-$B$3)+(C4-$C$3))
C) =SQRT((B4-$B$3)^2+(C4-$C$3)^2)
D) =(B4-$B$3)+(C4-$C$3)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
22
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell B7 of the spreadsheet for this problem?
A) = 30-.07 * C3
B) = 20 - .1 * B3
C) = B3- B4
D) = B5 * B7 + C5 * C7
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell B7 of the spreadsheet for this problem?
A) = 30-.07 * C3
B) = 20 - .1 * B3
C) = B3- B4
D) = B5 * B7 + C5 * C7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
23
An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. The following spreadsheet has been set up to solve the problem. What formula goes in cell B11 in this problem?
A) =B3*B7+B9/B3*B6+B9*2+B5*B7
B) =B3*B5+B3/B9*B6+B9/2*B5*B7
C) =SQRT(B3*B5+B3/B9*B6+B9/2*B5*B7)
D) =B3*B3+B3/B9+B6*B9/2*B5*B7
A) =B3*B7+B9/B3*B6+B9*2+B5*B7
B) =B3*B5+B3/B9*B6+B9/2*B5*B7
C) =SQRT(B3*B5+B3/B9*B6+B9/2*B5*B7)
D) =B3*B3+B3/B9+B6*B9/2*B5*B7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
24
An investor is developing a portfolio of stocks. She has identified 3 stocks to invest in. She wants to earn at least 5% return but with minimum risk. The problem data is given in the following Excel spreadsheet. What formula should be entered in cell G4 of the Excel spreadsheet? 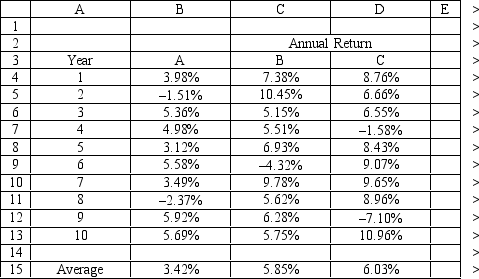
A) =COVAR(B4:B13)
B) =VARP(B4:B13)
C) =COVAR(B4:D13,$D$4:$B$13)
D) =COVAR(B4:B13,$B$4:$B$13)


A) =COVAR(B4:B13)
B) =VARP(B4:B13)
C) =COVAR(B4:D13,$D$4:$B$13)
D) =COVAR(B4:B13,$B$4:$B$13)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
25
An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. The following spreadsheet has been set up to solve the problem. What cell is the variable cell in this problem?
A) B3
B) B7
C) B9
D) B11
A) B3
B) B7
C) B9
D) B11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
26
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formula goes in cell D9 of the spreadsheet? 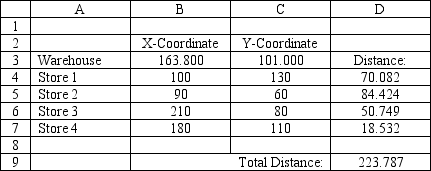
A) =MIN(D4:D7)^2
B) =SUM(D4:D7)
C) =SQRT(D4^2+D5^2+D6^2+D7^2)
D) =SQRT(MMULT(B3:C3,D4:D7))

A) =MIN(D4:D7)^2
B) =SUM(D4:D7)
C) =SQRT(D4^2+D5^2+D6^2+D7^2)
D) =SQRT(MMULT(B3:C3,D4:D7))

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
27
An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. The following spreadsheet has been set up to solve the problem. What cell is the objective cell in this problem?
A) B3
B) B7
C) B9
D) B11
A) B3
B) B7
C) B9
D) B11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
28
A company has collected the following inventory data for an item. What is the total annual cost for this item?
A) 275
B) 450
C) 5,275
D) 5,450
A) 275
B) 450
C) 5,275
D) 5,450

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
29
A company wants to locate a new warehouse to minimize the distance traveled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. Which cell(s) in the spreadsheet represent the decision variables in the problem? 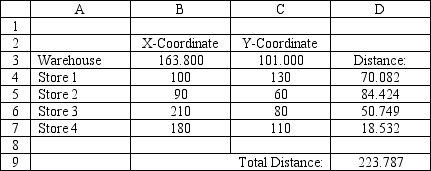
A) B3
B) B3:C3
C) B4:C7
D) D9

A) B3
B) B3:C3
C) B4:C7
D) D9

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
30
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell B9 of the spreadsheet for this problem?
A) =B3*B7+C3*C7
B) =B5*B7+C5*C7
C) =(B5-B4)*B7+(C5-C4)*B7
D) =B3*B7+C3*B7+B4*B7+C4*B7
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell B9 of the spreadsheet for this problem?
A) =B3*B7+C3*C7
B) =B5*B7+C5*C7
C) =(B5-B4)*B7+(C5-C4)*B7
D) =B3*B7+C3*B7+B4*B7+C4*B7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
31
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%, compounded quarterly, on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income. What formula goes in cell C7 of the spreadsheet? 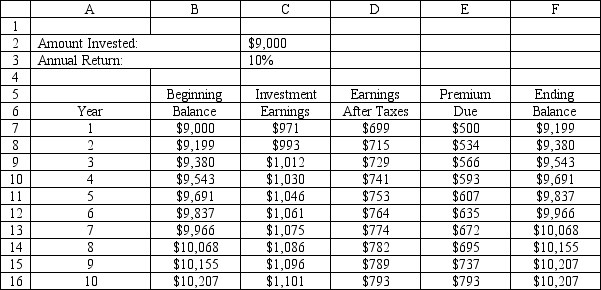
A) =B7*(1+$C$3/4)^4-B7
B) =B7*(1+$C$3)-B7
C) =B7*($C$3/4)^4-B7
D) =B7*(1+$C$3/4)^4

A) =B7*(1+$C$3/4)^4-B7
B) =B7*(1+$C$3)-B7
C) =B7*($C$3/4)^4-B7
D) =B7*(1+$C$3/4)^4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
32
Which of the following is not an assumption of an EOQ problem.
A) Demand for a product is fairly constant.
B) Inventory depletion rates vary non-linearly.
C) Each new order is delivered in full when the inventory level reaches 0.
D) All are valid assumptions.
A) Demand for a product is fairly constant.
B) Inventory depletion rates vary non-linearly.
C) Each new order is delivered in full when the inventory level reaches 0.
D) All are valid assumptions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
33
The Reduced Gradient is similar to which of these terms from linear programming?
A) Shadow Price
B) Allowable Decrease
C) Allowable Increase
D) Reduced Cost
A) Shadow Price
B) Allowable Decrease
C) Allowable Increase
D) Reduced Cost

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
34
Why does the GRG algorithm not provide allowable increase or allowable decrease information with the Reduced Gradient and Lagrange multiplier information?
A) Because all constraints have slack.
B) Because the constraints may not be linear.
C) Because the solution is not necessarily a global optimum.
D) Because the solutions are not necessarily corner points.
A) Because all constraints have slack.
B) Because the constraints may not be linear.
C) Because the solution is not necessarily a global optimum.
D) Because the solutions are not necessarily corner points.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
35
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $9,000 and hopes he can earn 12%, compounded quarterly, on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income. What constraint must be entered in the Risk Solver Platform (RSP) task pane? 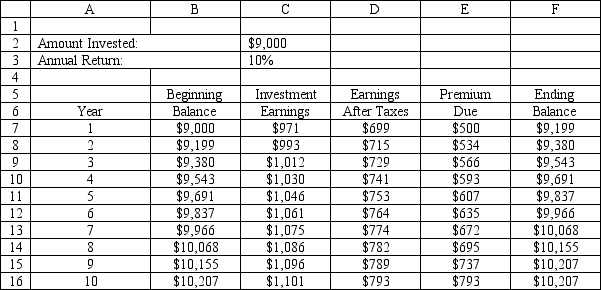
A) $D$7:$D$16 $E$7:$E$16
B) $C$7:$D$16 $E$7:$E$16
C) $C$7:$C$16 $E$7:$E$16
D) $D$7:$D$16 $E$7:$E$16

A) $D$7:$D$16 $E$7:$E$16
B) $C$7:$D$16 $E$7:$E$16
C) $C$7:$C$16 $E$7:$E$16
D) $D$7:$D$16 $E$7:$E$16

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
36
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of product A costs 25 to make and demand is estimated to be 20 ? .10 * Price of A. A unit of product B costs 18 to make and demand is estimated to be 30 ? .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs.
The objective function for this problem is?
A) MAX 25 X1 + 18 X2
B) MAX (20 ? 0.10*P1) X1 + (30 ? 0.07*P2) X2
C) MAX 20 P1 ? 0.1 P12 + 30 P2 ? 0.07 P22 ? 1040
D) MAX 22.5 P1 ? 0.1 P12 + 31.26 P2 ? 0.07 P22 ? 1040
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs.
The objective function for this problem is?
A) MAX 25 X1 + 18 X2
B) MAX (20 ? 0.10*P1) X1 + (30 ? 0.07*P2) X2
C) MAX 20 P1 ? 0.1 P12 + 30 P2 ? 0.07 P22 ? 1040
D) MAX 22.5 P1 ? 0.1 P12 + 31.26 P2 ? 0.07 P22 ? 1040

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
37
The Lagrange Multiplier is similar to which of these terms from linear programming?
A) Shadow Price
B) Allowable Increase
C) Allowable Decrease
D) Reduced Cost
A) Shadow Price
B) Allowable Increase
C) Allowable Decrease
D) Reduced Cost

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
38
An office supply company is attempting to determine the order quantity for laser printer toner cartridges which are sold to local businesses. Annual demand is 20,000 units and each cartridge costs the store $25. It costs $30 to place an order and the inventory carrying cost rate is 25% of the value of the item. The following spreadsheet has been set up to solve the problem. What constraint would you impose on this problem to ensure that at least one order is placed per year?
A) MAX B9
B) B9 = 1
C) B9 ? 1
D) MIN B11
A) MAX B9
B) B9 = 1
C) B9 ? 1
D) MIN B11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
39
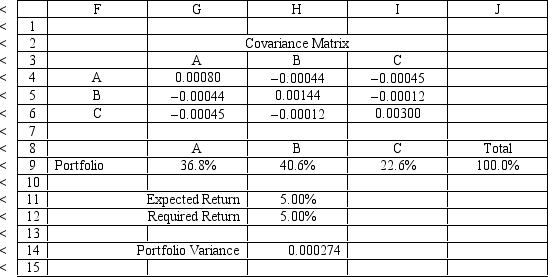
An investor is developing a portfolio of stocks. She has identified 3 stocks to invest in. She wants to earn at least 5% return but with minimum risk. The problem data is given in the following Excel spreadsheet. What formula should be entered in cell H11 of the Excel spreadsheet? 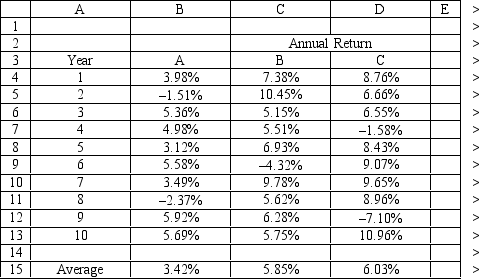
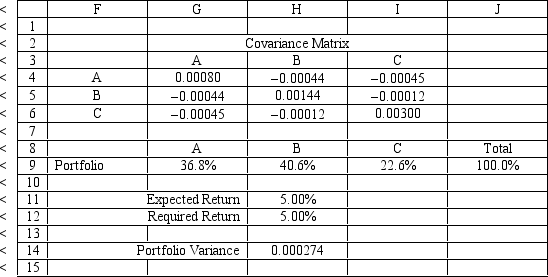
A) =SUMPRODUCT(B15:D15,G9:I9)
B) =SUMPRODUCT(B15:D15,B4:D13)
C) =SUMPRODUCT(B15:D15,I9)
D) =SUMPRODUCT(B15:D15,G4:I6)


A) =SUMPRODUCT(B15:D15,G9:I9)
B) =SUMPRODUCT(B15:D15,B4:D13)
C) =SUMPRODUCT(B15:D15,I9)
D) =SUMPRODUCT(B15:D15,G4:I6)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
40
Exhibit 8.1
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell D12 of the spreadsheet for this problem?
A) =SUMPRODUCT(B3:C3, B12:C12)
B) =SUMPRODUCT(B4:C4, B12:C12)
C) =SUMPRODUCT(B5:C5, B12:C12)
D) =SUMPRODUCT(B7:C7, B12:C12)
The following questions pertain to the problem and spreadsheet below.
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 25 to make and demand is estimated to be 20 - .10 * Price of A. A unit of B costs 18 to make and demand is estimated to be 30 - .07 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 100 and 200.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs
-Refer to Exhibit 8.1. What formula is used in cell D12 of the spreadsheet for this problem?
A) =SUMPRODUCT(B3:C3, B12:C12)
B) =SUMPRODUCT(B4:C4, B12:C12)
C) =SUMPRODUCT(B5:C5, B12:C12)
D) =SUMPRODUCT(B7:C7, B12:C12)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
41
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 30 to make and demand is estimated to be 50- 0.09 * Price of A. A unit of B costs 20 to make and demand is estimated to be 30- 0.14 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 90 and 140.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs.
The NLP for the problem is:
:
What values should go in cells B3:E18 of the spreadsheet for this problem?
.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs.
The NLP for the problem is:
:
What values should go in cells B3:E18 of the spreadsheet for this problem?
.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
42
A company wants to locate a new warehouse to minimize the distance travelled by its delivery trucks. It has four stores and their coordinates are listed in the accompanying spreadsheet. What formulas should go in cells D4:D9 of the spreadsheet for this problem?
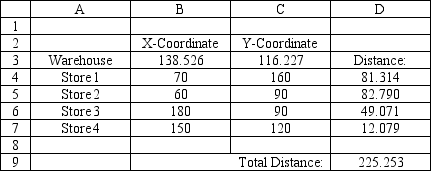


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
43
How much must the objective function coefficient of the variable Pumpkin change before any Pumpkins are produced based on the following sensitivity report?
A) increase by 12
B) decrease by 12
C) increase by 499.99
D) decrease by 499.99
A) increase by 12
B) decrease by 12
C) increase by 499.99
D) decrease by 499.99

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
44
The Sweet Water beverage company is designing a new soft drink can. The designers wish to minimize the manufacturing cost of the can, a cost that is directly related to the amount of aluminum used in the can. The can must hold at least 350 ml (or cm3) of beverage, have a diameter between 3 and 7 cm, and have a height between 7 and 19 cm.
Formulate the NLP for Sweet Water.
Formulate the NLP for Sweet Water.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the maximum solution on this graph of a function starting from X = 12. Mark its location on the graph.
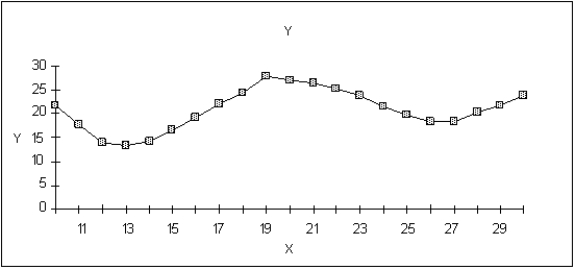


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
46
An office supply company is attempting to determine the order quantity for Mt. White fountain pens which are sold to local executives. Annual demand is 5,000 units and each pen costs the store $50. It costs $75 to place an order and the inventory carrying cost rate is 30% of the value of the item.
Formulate the objective function for this problem. Let Q indicate the order quantity.
Formulate the objective function for this problem. Let Q indicate the order quantity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
47
A company wants to locate a new warehouse to minimize the longest distance travelled by any of its delivery trucks. It has four stores and their coordinates are listed in the below.
 Let X and Y represent the X, Y coordinates of the new warehouse. The NLP for this problem and solution is the following.
Let X and Y represent the X, Y coordinates of the new warehouse. The NLP for this problem and solution is the following.

 Let X and Y represent the X, Y coordinates of the new warehouse. The NLP for this problem and solution is the following.
Let X and Y represent the X, Y coordinates of the new warehouse. The NLP for this problem and solution is the following.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
48
Calculate the annual inventory costs for the following data.



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
49
An office supply company is attempting to determine the order quantity for Mt. White fountain pens which are sold to local executives. Annual demand is 5,000 units and each pen costs the store $50. It costs $75 to place an order and the inventory carrying cost rate is 30% of the value of the item.
What values should go in cells B3:B11 of the spreadsheet for this problem if Q = 223.61?
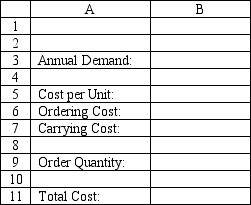
What values should go in cells B3:B11 of the spreadsheet for this problem if Q = 223.61?


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
50
How much must the objective function coefficient of the variable X2 increase before any X2s are produced based on the following sensitivity report?



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
51
An investor is developing a portfolio of stocks. She has identified 3 stocks in which to invest. She wants to earn at least 11% return but with minimum risk.
The average return for the stocks is:
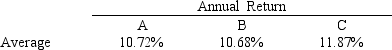 The covariance matrix for the stocks is:
The covariance matrix for the stocks is:
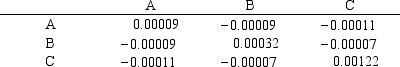 Let: Pi = proportion of total funds invested in i, i = A, B, C
Let: Pi = proportion of total funds invested in i, i = A, B, C
Formulate the NLP for this problem.
The average return for the stocks is:
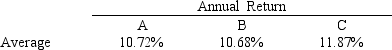 The covariance matrix for the stocks is:
The covariance matrix for the stocks is: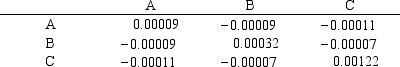 Let: Pi = proportion of total funds invested in i, i = A, B, C
Let: Pi = proportion of total funds invested in i, i = A, B, CFormulate the NLP for this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
52
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $12,000 and hopes he can earn 18% on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income.
What formulas should go in cells B7:F7 of the spreadsheet for this problem?
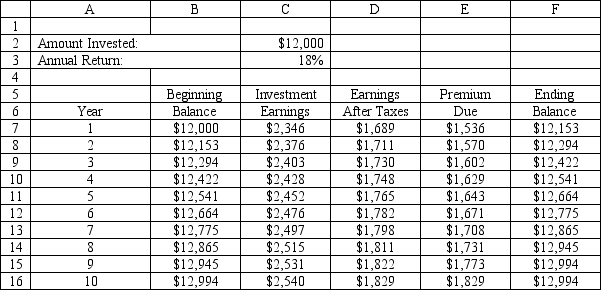
What formulas should go in cells B7:F7 of the spreadsheet for this problem?


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
53
A company makes products A and B from 2 resources, labor and material. The company wants to determine the selling price which will maximize profits. A unit of A costs 30 to make and demand is estimated to be 50 .09 * Price of A. A unit of B costs 20 to make and demand is estimated to be 30 .14 * Price of B. The utilization of labor and materials and the available quantity of resources is shown in the table. A reasonable price for the products is between 90 and 140.
 Let X1 = demand for As and X2 = demand for Bs.
Let X1 = demand for As and X2 = demand for Bs.
Let P1 = price for As and P2 = price for Bs.
Formulate the NLP for this company
 Let X1 = demand for As and X2 = demand for Bs.
Let X1 = demand for As and X2 = demand for Bs.Let P1 = price for As and P2 = price for Bs.
Formulate the NLP for this company

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
54
An investor is developing a portfolio of stocks. She has identified 3 stocks in which to invest. She wants to earn at least 11% return but with minimum risk.
Let: Pi = proportion of total funds invested in i, i = A, B, C
The NLP for this problem is:
 What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
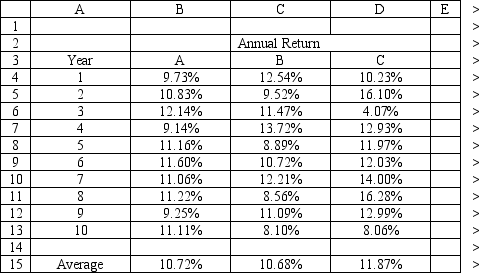
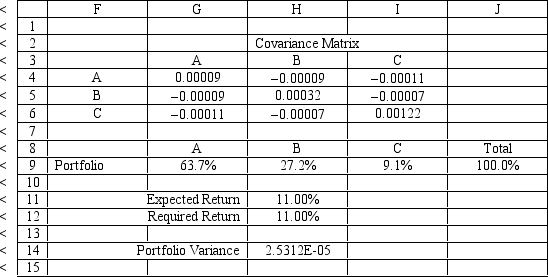
Let: Pi = proportion of total funds invested in i, i = A, B, C
The NLP for this problem is:
 What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.
What formulas should go in cells G4:J14 of the spreadsheet for this problem? NOTE: Formulas are not required in all of these cells.


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
55
How much are additional units of Labor worth based on the following sensitivity report?
A) 0
B) 1.21
C) 2.57
D) 9.42
A) 0
B) 1.21
C) 2.57
D) 9.42

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
56
A company wants to locate a new warehouse to minimize the distance travelled by its delivery trucks. It has four stores and their coordinates are listed in the below.
 Formulate the objective function for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
Formulate the objective function for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
 Formulate the objective function for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
Formulate the objective function for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
57
An investor wants to determine how much interest he must earn to be able to make the payments on a 10-year mortgage which has increasing annual payments. The problem is summarized in the accompanying spreadsheet. The investor has enough money to make an initial investment of $12,000 and hopes he can earn 18% on his investments. He would like to know how low his annual return can be and still allow him to make his payments from interest income.
If the Risk Solver Platform (RSP) is used, which are the Objective, Variables and Constraint cells in the spreadsheet for this problem?
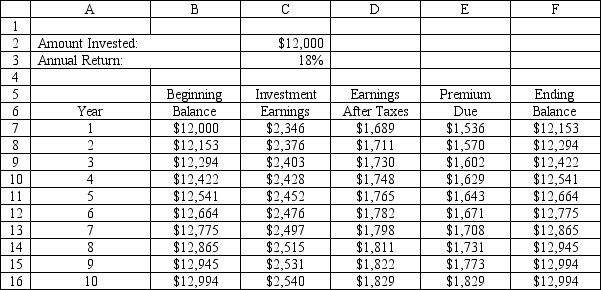
If the Risk Solver Platform (RSP) is used, which are the Objective, Variables and Constraint cells in the spreadsheet for this problem?


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
58
How many local minimum solutions are there on this graph of a function Mark their locations on the graph.
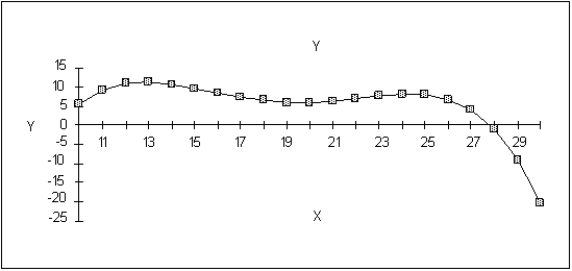


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
59
How many local maximum solutions are there on this graph of a function? Mark their locations on the graph.
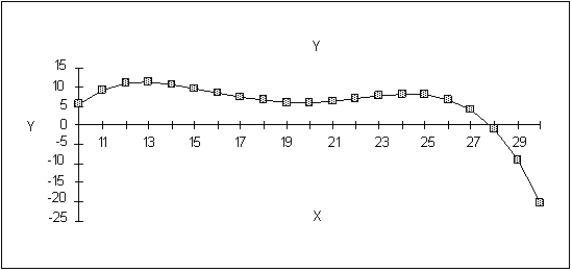


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
60
A company wants to locate a new warehouse to minimize the longest distance travelled by any of its delivery trucks. It has four stores and their coordinates are listed in the below.
 Formulate the NLP for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
Formulate the NLP for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
 Formulate the NLP for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
Formulate the NLP for this problem. Let X and Y represent the X, Y coordinates of the new warehouse.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
61
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2. What formula would you place in cell B6 to calculate Total Lot Area?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.-Refer to Exhibit 8.2. What formula would you place in cell B6 to calculate Total Lot Area?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
62
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2. What values would you enter in the Risk Solver Platform (RSP) task pane for the above Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.-Refer to Exhibit 8.2. What values would you enter in the Risk Solver Platform (RSP) task pane for the above Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
63
How much are additional units of labor worth based on the following sensitivity report?
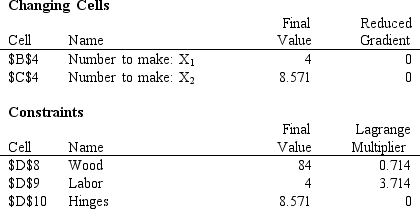
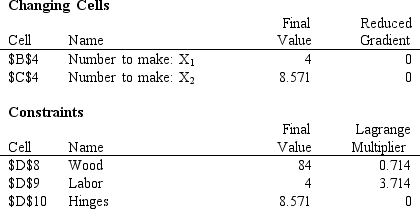

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
64
A construction company just purchased a 300 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
Formulate the NLP for the problem.
Formulate the NLP for the problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
65
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2. The company wishes to have a relatively square building. Thus, they wish neither the building length nor the building width exceed the other by more than 25%. Add constraint(s) to enforce this design constraint.
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.-Refer to Exhibit 8.2. The company wishes to have a relatively square building. Thus, they wish neither the building length nor the building width exceed the other by more than 25%. Add constraint(s) to enforce this design constraint.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
66
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2. What formula would you place into cell B5 to calculate Total Floor Area?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.-Refer to Exhibit 8.2. What formula would you place into cell B5 to calculate Total Floor Area?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
67
Exhibit 8.2
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.
-Refer to Exhibit 8.2. What formula would you place in cell D13 to calculate total cost?
The following questions pertain to the problem and spreadsheet below.
A construction company just purchased a 300 x 300 foot lot upon which they plan to build an office building. They need at least 60,000 ft2 of office floor space. Zoning regulations require each floor be 10 feet high and the building not exceed 65 ft in height. Further, parking space must equal at least 30% of the total floor space available. The company's cost accountant uses a 60% factor of the building height and a 1% factor of any story's floor area to calculate the total building cost (in millions of dollars).
The following is the NLP formulation for the problem.
 The spreadsheet implementation of this formulation applies to the following questions.
The spreadsheet implementation of this formulation applies to the following questions.-Refer to Exhibit 8.2. What formula would you place in cell D13 to calculate total cost?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck
68
Project 8.1 - Truck Company Expansion
Kornfield Trucking handles private and commercial moves. They currently own 500 moving vans and employ 2000 full-time workers. Their trucks are used to pick-up and deliver office and household goods throughout the Eastern and Southeastern states. Kornfield mans each truck with three workers. This allows driver swaps providing increased miles-covered-per-hour ratio while staying within safety requirements for individual driving time. A 3-person crew also reduces company reliance on local help. Local distributors and warehouses provide a pool of laborers for loading and unloading the moving trucks. While in the past this arrangement has worked well, the arrangement has soured recently as the temporary workers have demanded higher wages while produced less work. Despite their pay and benefits package, Kornfield still finds that the nature of the work (lifting and time on the road) makes for a high rate of turnover. Thus, Kornfield maintains an excess of workers/drivers, but no more than 3.75 workers per truck at any time.
The following information is available on the trucks in the Kornfield inventory and their options for new purchases.
The following information applies to Kornfield personnel actions.
Kornfield has an operating budget of $ 75M next year and wants to expand their operations. As a part of this expansion, they are considering options for their truck fleet and may purchase new trucks, sell old trucks to salvage or some combination of the two. Any salvage money received is rolled into the operating budget. Kornfield is also considering possible changes to their work force. Their current force has a fairly high average salary and their operating budget is not greatly affected by releasing current employees. On the other hand, newer employees carry a much lower average salary and do not tax the operating budget heavily in hiring and training costs.
The Cobb-Douglas production function is used to model the number of vehicle miles driven per year. This function represents the quantity Kornfield management would like to maximize as they expand their operations. The general form of the Cobb-Douglas production function is the following:
where y is the output, each Xi represents an input and the letters represent constants. This function generalizes to fewer or a greater number of parameters than the three depicted above. The constants for the Kornfield Trucking production function are (a, b, c, d) = (9.1, 0.05, 0.40, 0.50).
Formulate the Kornfield Trucking problem as a non-linear programming problem. Implement the problem in Excel and use Risk Solver Platform (RSP) generalized reduced gradient (GRG) routing to obtain a solution to the problem. What is a recommended solution for Kornfield Trucking?
Kornfield Trucking handles private and commercial moves. They currently own 500 moving vans and employ 2000 full-time workers. Their trucks are used to pick-up and deliver office and household goods throughout the Eastern and Southeastern states. Kornfield mans each truck with three workers. This allows driver swaps providing increased miles-covered-per-hour ratio while staying within safety requirements for individual driving time. A 3-person crew also reduces company reliance on local help. Local distributors and warehouses provide a pool of laborers for loading and unloading the moving trucks. While in the past this arrangement has worked well, the arrangement has soured recently as the temporary workers have demanded higher wages while produced less work. Despite their pay and benefits package, Kornfield still finds that the nature of the work (lifting and time on the road) makes for a high rate of turnover. Thus, Kornfield maintains an excess of workers/drivers, but no more than 3.75 workers per truck at any time.
The following information is available on the trucks in the Kornfield inventory and their options for new purchases.
The following information applies to Kornfield personnel actions.
Kornfield has an operating budget of $ 75M next year and wants to expand their operations. As a part of this expansion, they are considering options for their truck fleet and may purchase new trucks, sell old trucks to salvage or some combination of the two. Any salvage money received is rolled into the operating budget. Kornfield is also considering possible changes to their work force. Their current force has a fairly high average salary and their operating budget is not greatly affected by releasing current employees. On the other hand, newer employees carry a much lower average salary and do not tax the operating budget heavily in hiring and training costs.
The Cobb-Douglas production function is used to model the number of vehicle miles driven per year. This function represents the quantity Kornfield management would like to maximize as they expand their operations. The general form of the Cobb-Douglas production function is the following:
where y is the output, each Xi represents an input and the letters represent constants. This function generalizes to fewer or a greater number of parameters than the three depicted above. The constants for the Kornfield Trucking production function are (a, b, c, d) = (9.1, 0.05, 0.40, 0.50).
Formulate the Kornfield Trucking problem as a non-linear programming problem. Implement the problem in Excel and use Risk Solver Platform (RSP) generalized reduced gradient (GRG) routing to obtain a solution to the problem. What is a recommended solution for Kornfield Trucking?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 68 في هذه المجموعة.
فتح الحزمة
k this deck








