Deck 11: Analytic Geometry In Three Dimensions
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/256
العب
ملء الشاشة (f)
Deck 11: Analytic Geometry In Three Dimensions
1
Find a set of symmetric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Parametric equations:
3
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Parametric equations:
4
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
5
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: (5,0,2)
Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: (5,0,2)
Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
A)
B)
C)
D)
E)
Point: Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
7
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
8
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
9
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
A)
B)
C)
D)
E)
Point: Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
A)
B)
C)
D)
E)
Point: Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: (0,0,0)
Perpendicular to:
A)
B)
C)
D)
E)
Point: (0,0,0)
Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
12
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: (0,0,0)
Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: (0,0,0)
Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
14
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
15
Find a set of parametric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
16
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
A)
B)
C)
D)
E)
Point: Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
18
Find a set of parametric equations for the line through the point and parallel to the specified vector or line.(For each line,write the direction numbers as integers. )
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:
Point: Parallel to:
A)Parametric equations:
B)Parametric equations:
C)Parametric equations:
D)Parametric equations:
E)Parametric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
19
Find a set of symmetric equations for the line through the point and parallel to the specified vector or line.
Point: (7,0,0)
Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:
Point: (7,0,0)
Parallel to:
A)Symmetric equations:
B)Symmetric equations:
C)Symmetric equations:
D)Symmetric equations:
E)Symmetric equations:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector or line.
Point: Perpendicular to:
A)
B)
C)
D)
E)
Point: Perpendicular to:
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
21
Find a set of parametric equations of the line.
Passes through and is parallel to the xz-plane and the yz-plane
A)
B)
C)
D)
E)
Passes through and is parallel to the xz-plane and the yz-plane
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
22
Find the general form of the equation of the plane passing through the three points.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (-4,4,-1), (1,6,2), (-5,-3,6)
A)35x -38y -33z = 0
B)4x -4y 1z = 0
C)4x -4y 1z + 259 = 0
D)35x -38y -33z + 259 = 0
E)35x -38y -33z - 259 = 0
A)35x -38y -33z = 0
B)4x -4y 1z = 0
C)4x -4y 1z + 259 = 0
D)35x -38y -33z + 259 = 0
E)35x -38y -33z - 259 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
23
Find a set of parametric equations of the line.
Passes through and is parallel to the xy-plane and the yz-plane
A)
B)
C)
D)
E)
Passes through and is parallel to the xy-plane and the yz-plane
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
24
Find the general form of the equation of the plane with the given characteristics. The plane passes through the point (-2,-3,-5)and is parallel to the yz-plane.
A)x + y + z = -10
B)y = -3
C)z = -5
D)y + z = -8
E)x = -2
A)x + y + z = -10
B)y = -3
C)z = -5
D)y + z = -8
E)x = -2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
25
Find a set of parametric equations of the line.
Passes through and is perpendicular to .
A)
B)
C)
D)
E)
Passes through and is perpendicular to .
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the general form of the equation of the plane passing through the point and perpendicular to the specified line.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.]
A)7x + 8y + z + 2 = 0
B)7x + 8y + z - 2 = 0
C)x - y + 2z - 1 = 0
D)x - y + 2z + 1 = 0
E)x - y + 2z = 0
A)7x + 8y + z + 2 = 0
B)7x + 8y + z - 2 = 0
C)x - y + 2z - 1 = 0
D)x - y + 2z + 1 = 0
E)x - y + 2z = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
27
Find a set of symmetric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
28
Find a set of symmetric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
29
Determine whether the planes are parallel,orthogonal,or neither.
x + 2y + z = 6
-2x - 4y - 2z = -10
A)orthogonal
B)parallel
C)neither
x + 2y + z = 6
-2x - 4y - 2z = -10
A)orthogonal
B)parallel
C)neither

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (-4,5,6),n = 2i- 4j+ 4k
A)x - 2y + 2 z + 2 = 0
B)4x - 5y - 6z + 4 = 0
C)x - 2y + 2 z - 2 = 0
D)x - 2y + 2 z = 0
E)4x - 5y - 6z - 4 = 0
A)x - 2y + 2 z + 2 = 0
B)4x - 5y - 6z + 4 = 0
C)x - 2y + 2 z - 2 = 0
D)x - 2y + 2 z = 0
E)4x - 5y - 6z - 4 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
31
Find the general form of the equation of the plane with the given characteristics. The plane passes through the points (3,-2,-7)and (-2,6,3)and is perpendicular to the plane -x - 4y - z = 4.
A)32x - 15y + 28z - 262 = 0
B)31x - 16y + 30z + 85 = 0
C)x + 4y + z = 0
D)32x + 15y + 28z - 130 = 0
E)x + 4y + z - 12 = 0
A)32x - 15y + 28z - 262 = 0
B)31x - 16y + 30z + 85 = 0
C)x + 4y + z = 0
D)32x + 15y + 28z - 130 = 0
E)x + 4y + z - 12 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
32
Find a set of parametric equations of the line.
Passes through and is perpendicular to .
A)
B)
C)
D)
E)
Passes through and is perpendicular to .
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
33
Determine whether the planes are parallel,orthogonal,or neither.
5x - 2y - 5z = -2
X - 3y + 6z = -6
A)neither
B)parallel
C)orthogonal
5x - 2y - 5z = -2
X - 3y + 6z = -6
A)neither
B)parallel
C)orthogonal

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
34
Find a set of parametric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find the angle of intersection of the planes in degrees.Round to a tenth of a degree.
3x + 2y - 6z = -5
-6x + 3y + z = 1
A)112.3°
B)2.0°
C)-22.3°
D)109.4°
E)20.8°
3x + 2y - 6z = -5
-6x + 3y + z = 1
A)112.3°
B)2.0°
C)-22.3°
D)109.4°
E)20.8°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
36
Determine whether the planes are parallel,orthogonal,or neither. 5x - y + z = -4
-x - 6y - z = -2
A)neither
B)orthogonal
C)parallel
-x - 6y - z = -2
A)neither
B)orthogonal
C)parallel

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find a set of parametric equations of the line that passes through the given points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
38
Find a set of parametric equations of the line.
Passes through and is parallel to .
A)
B)
C)
D)
E)
Passes through and is parallel to .
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
39
Find the general form of the equation of the plane with the given characteristics.
Passes through and is parallel to the yz-plane
A)
B)
C)
D)
E)
Passes through and is parallel to the yz-plane
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
40
Find the general form of the equation of the plane with the given characteristics.
Passes through and is parallel to the xz-plane
A)
B)
C)
D)
E)
Passes through and is parallel to the xz-plane
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find the angle between the two planes.
A)71.5
B)72.5
C)73.5
D)70.5
E)69.5
A)71.5
B)72.5
C)73.5
D)70.5
E)69.5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
42
Determine whether the planes are parallel,orthogonal,or neither.
A)Neither
B)Orthogonal
C)Parallel
A)Neither
B)Orthogonal
C)Parallel

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the general form of the equation of the plane passing through the point and perpendicular to the specified vector.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (6,2,9),n = 8i + 6j + 9k
A)8x + 6y + 9 z = 0
B)8x + 6y + 9 z + 141 = 0
C)8x + 6y + 9 z - 141 = 0
D)6x + 2y + 9z + 141 = 0
E)6x + 2y + 9z - 141 = 0
A)8x + 6y + 9 z = 0
B)8x + 6y + 9 z + 141 = 0
C)8x + 6y + 9 z - 141 = 0
D)6x + 2y + 9z + 141 = 0
E)6x + 2y + 9z - 141 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
44
Determine whether the planes are parallel,orthogonal,or neither.
5x - 6y - 6z = 0
3x - 4y + 2z = -4
A)parallel
B)orthogonal
C)neither
5x - 6y - 6z = 0
3x - 4y + 2z = -4
A)parallel
B)orthogonal
C)neither

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the angle of intersection of the planes in degrees.Round to a tenth of a degree. 5x + y - z = -3
-3x - y + z = -1
A)167.7°
B)-80.6°
C)170.6°
D)44.6°
E)3.0°
-3x - y + z = -1
A)167.7°
B)-80.6°
C)170.6°
D)44.6°
E)3.0°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find the general form of the equation of the plane passing through the three points.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.] (3,1,6), (-6,-1,6), (3,5,-6)
A)2x - 9y - 3z + 21 = 0
B)2x - 9y - 3z = 0
C)3x + y + 6z = 0
D)2x - 9y - 3z - 21 = 0
E)3x + y + 6z - 252 = 0
A)2x - 9y - 3z + 21 = 0
B)2x - 9y - 3z = 0
C)3x + y + 6z = 0
D)2x - 9y - 3z - 21 = 0
E)3x + y + 6z - 252 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find a set of parametric equations of the line.
Passes through and is parallel to .
A)
B)
C)
D)
E)
Passes through and is parallel to .
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find the general form of the equation of the plane passing through the three points.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find the angle between the two planes in degrees.Round to a tenth of a degree.
3x - 4y + z = -6
2x + y + 3z = 0
A)15.2°
B)71.9°
C)14.7°
D)74.8°
E)1.3°
3x - 4y + z = -6
2x + y + 3z = 0
A)15.2°
B)71.9°
C)14.7°
D)74.8°
E)1.3°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find the general form of the equation of the plane with the given characteristics. The plane passes through the point (5,-1,-4)and is parallel to the yz-plane.
A)y = -1
B)z = -4
C)x + y + z = 0
D)y + z = -5
E)x = 5
A)y = -1
B)z = -4
C)x + y + z = 0
D)y + z = -5
E)x = 5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
51
Determine whether the planes are parallel,orthogonal,or neither.
5x - 4y + z = -2
3x + 4y + z = -5
A)parallel
B)orthogonal
C)neither
5x - 4y + z = -2
3x + 4y + z = -5
A)parallel
B)orthogonal
C)neither

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
52
Find the general form of the equation of the plane with the given characteristics. The plane passes through the points (5,5,-2)and (4,2,1)and is perpendicular to the plane -3x - 2y + 4z = 1.
A)6x + 5y + 7z - 41 = 0
B)3x + 2y - 4z + 33 = 0
C)6x - 5y + 7z - 9 = 0
D)3x + 2y - 4z = 0
E)7x + 6y + 5z - 55 = 0
A)6x + 5y + 7z - 41 = 0
B)3x + 2y - 4z + 33 = 0
C)6x - 5y + 7z - 9 = 0
D)3x + 2y - 4z = 0
E)7x + 6y + 5z - 55 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
53
Determine whether the planes are parallel,orthogonal,or neither.
A)Neither
B)Parallel
C)Orthogonal
A)Neither
B)Parallel
C)Orthogonal

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
54
Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] ![<strong>Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)</strong> A)54.7° B)30° C)2.1° D)90° E)45°](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9df7_6475_a6c3_396fc389cbdf_TB7698_00.jpg) P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)
P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)
A)54.7°
B)30°
C)2.1°
D)90°
E)45°
![<strong>Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)</strong> A)54.7° B)30° C)2.1° D)90° E)45°](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9df7_6475_a6c3_396fc389cbdf_TB7698_00.jpg) P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)
P(8,0,0),Q(8,8,0),R(0,8,0),S(4,4,4)A)54.7°
B)30°
C)2.1°
D)90°
E)45°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
55
Find the angle between the two planes.
A)81.6°
B)83.2°
C)83.8°
D)80.6°
E)79.6°
A)81.6°
B)83.2°
C)83.8°
D)80.6°
E)79.6°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
56
Determine whether the planes are parallel,orthogonal,or neither.
6x + y - z = 2
-18x - 3y + 3z = -4
A)parallel
B)orthogonal
C)neither
6x + y - z = 2
-18x - 3y + 3z = -4
A)parallel
B)orthogonal
C)neither

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
57
Find the angle between the two planes in degrees.Round to a tenth of a degree.
5x - 6y - 4z = -5
X + y + 5z = -1
A)114.5°
B)27.4°
C)117.4°
D)24.7°
E)2.0°
5x - 6y - 4z = -5
X + y + 5z = -1
A)114.5°
B)27.4°
C)117.4°
D)24.7°
E)2.0°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
58
Find the angle between the two planes in degrees.Round to a tenth of a degree.
A)88.0°
B)90.8°
C)10.8°
D)89.8°
E)89.7°
A)88.0°
B)90.8°
C)10.8°
D)89.8°
E)89.7°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find the angle between the two planes.
A)77.7°
B)76.7°
C)79.7°
D)78.7°
E)75.7°
A)77.7°
B)76.7°
C)79.7°
D)78.7°
E)75.7°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
60
Find the general form of the equation of the plane passing through the point and perpendicular to the specified line.[Be sure to reduce the coefficients in your answer to lowest terms by dividing out any common factor.]
A)x + 3y + 5z = 0
B)x + 3y + 5z - 29 = 0
C)x + 3y + 5z + 29 = 0
D)3x - 3y + 7z - 29 = 0
E)3x - 3y + 7z + 29 = 0
A)x + 3y + 5z = 0
B)x + 3y + 5z - 29 = 0
C)x + 3y + 5z + 29 = 0
D)3x - 3y + 7z - 29 = 0
E)3x - 3y + 7z + 29 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find u × v and show that it is orthogonal to both u and v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
62
Find u × v and show that it is orthogonal to both u and v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
63
Find symmetric equations for the line through the point and parallel to the specified vector.
(9,-6,-5),parallel to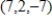
(9,-6,-5),parallel to
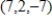

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
64
Find a set of parametric equations for the line through the point and parallel to the specified vector. 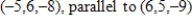
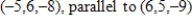

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
65
Find symmetric equations for the line through the point and parallel to the specified line. 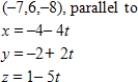
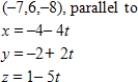

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find a set of parametric equations for the line that passes through the given points. 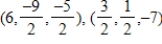
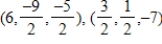

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
67
Use the vectors u and v to find u × v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
68
Use the vectors u and v to find v × u.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
69
Use the vectors u and v to find (3u)× v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
70
Use the vectors u and v to find u × (2v).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find u × v and show that it is orthogonal to both u and v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find u × v and show that it is orthogonal to both u and v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
73
Use the vectors u and v to find u × (-v).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
74
Use the vectors u and v to find (-2u)× v.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find the distance between the point and the plane.
(-5,-6,-5)
A)18
B)
C)
D)0
E)
(-5,-6,-5)
A)18
B)
C)
D)0
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
76
Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] ![<strong>Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)</strong> A)2.6° B)47.1° C)90° D)45° E)59.5°](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9df8_9d12_a6c3_b93c12b709ec_TB7698_00.jpg) P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)
P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)
A)2.6°
B)47.1°
C)90°
D)45°
E)59.5°
![<strong>Find the angle,in degrees,between two adjacent sides of the pyramid shown below.Round to the nearest tenth of a degree.[Note: The base of the pyramid is not considered a side.] P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)</strong> A)2.6° B)47.1° C)90° D)45° E)59.5°](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9df8_9d12_a6c3_b93c12b709ec_TB7698_00.jpg) P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)
P(10,0,0),Q(10,10,0),R(0,10,0),S(5,5,2)A)2.6°
B)47.1°
C)90°
D)45°
E)59.5°

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
77
Find a set of parametric equations for the line through the point and parallel to the specified line. 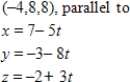
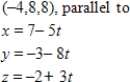

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
78
Use the vectors u and v to find v × (u × u).
A)v × (u × u)= -12
B)v × (u × u)= 0
C)v × (u × u)= 12
D)v × (u × u)= -11
E)v × (u × u)= 11
A)v × (u × u)= -12
B)v × (u × u)= 0
C)v × (u × u)= 12
D)v × (u × u)= -11
E)v × (u × u)= 11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
79
Find a set of parametric equations for the line that passes through the given points.
(8,2,3), (-1,3,-6)
(8,2,3), (-1,3,-6)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck
80
Use the vectors v to find v×v.
A)v × v = -8
B)v × v = -7
C)v × v = 0
D)v × v = 8
E)v × v = 7
A)v × v = -8
B)v × v = -7
C)v × v = 0
D)v × v = 8
E)v × v = 7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 256 في هذه المجموعة.
فتح الحزمة
k this deck








