Deck 1: Functions and Their Graphs
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/513
العب
ملء الشاشة (f)
Deck 1: Functions and Their Graphs
1
Select the graph of the function, and use the Horizontal Line Test to determine whether the function is one-to-one and so has an inverse function.
A)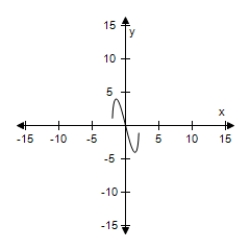 The function does not have inverse.
The function does not have inverse.
B)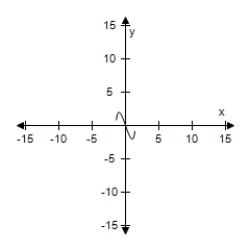 The function does not have inverse.
The function does not have inverse.
C)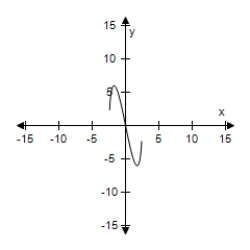 The function does not have inverse.
The function does not have inverse.
D)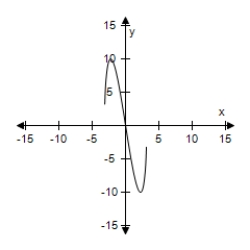 The function does not have inverse.
The function does not have inverse.
E)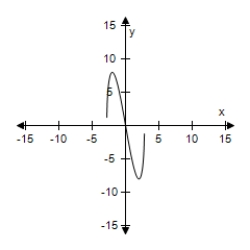 The function does not have inverse.
The function does not have inverse.
A)
 The function does not have inverse.
The function does not have inverse.B)
 The function does not have inverse.
The function does not have inverse.C)
 The function does not have inverse.
The function does not have inverse.D)
 The function does not have inverse.
The function does not have inverse.E)
 The function does not have inverse.
The function does not have inverse. The function does not have inverse.
The function does not have inverse. 2
Select the correct graph, showing f and g are inverse functions.
A)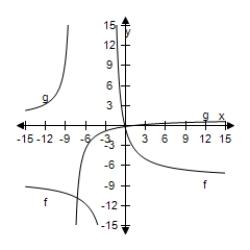
B)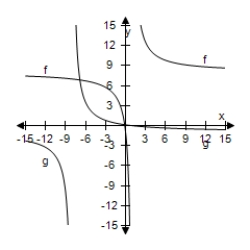
C)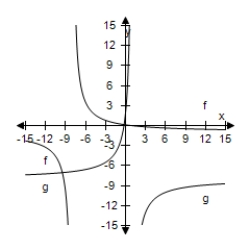
D)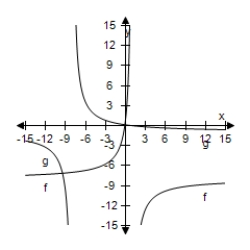
E)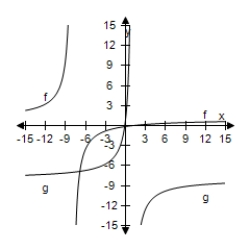
A)

B)

C)

D)

E)


3
Select the graph of the function, and use the Horizontal Line Test to determine whether the function is one-to-one and so has an inverse function.
G(x) = |x + 5| - |x - 5|
A)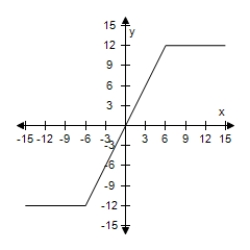 The function does not have inverse.
The function does not have inverse.
B)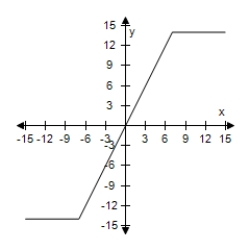 The function does not have inverse.
The function does not have inverse.
C)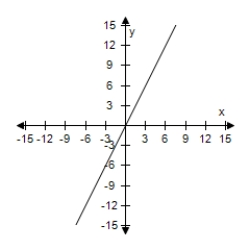 The function does not have inverse.
The function does not have inverse.
D)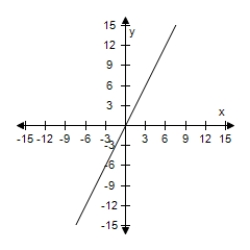 The function does not have inverse.
The function does not have inverse.
E)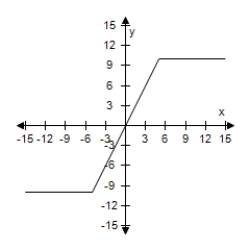 The function does not have inverse.
The function does not have inverse.
G(x) = |x + 5| - |x - 5|
A)
 The function does not have inverse.
The function does not have inverse.B)
 The function does not have inverse.
The function does not have inverse.C)
 The function does not have inverse.
The function does not have inverse.D)
 The function does not have inverse.
The function does not have inverse.E)
 The function does not have inverse.
The function does not have inverse. The function does not have inverse.
The function does not have inverse. 4
Find the inverse function of f informally.
F(x) = x - 5
A)f-1(x) = - (x + 5)
B)
C)
D)f-1(x) = 5 - x
E)f-1(x) = x + 5
F(x) = x - 5
A)f-1(x) = - (x + 5)
B)
C)
D)f-1(x) = 5 - x
E)f-1(x) = x + 5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
5
Determine whether the function has an inverse function.If it does, find the inverse function.
A)
B)
C)
D)
E)No inverse
A)
B)
C)
D)
E)No inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
6
Select the correct graph, showing f and g are inverse functions.
A)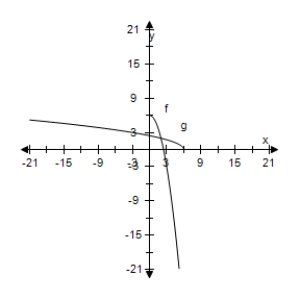
B)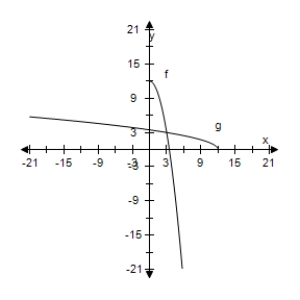
C)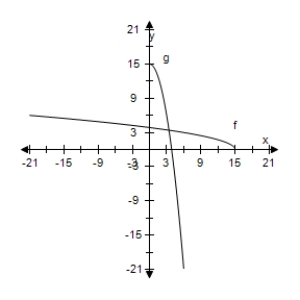
D)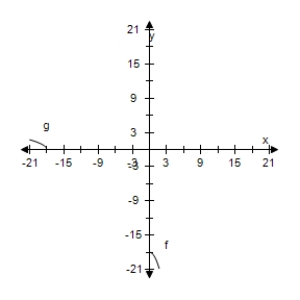
E)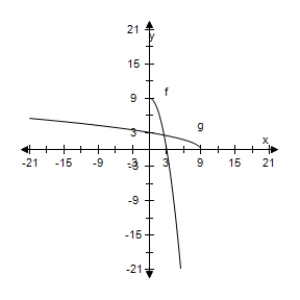
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
7
Does the function have an inverse function? 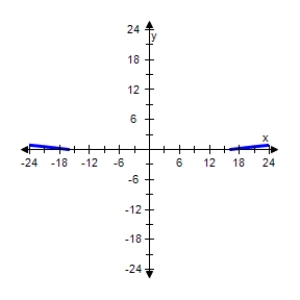


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
8
Select the graph of f and f-1 on the same set of coordinate axes.
F(x) = 2x - 3
A)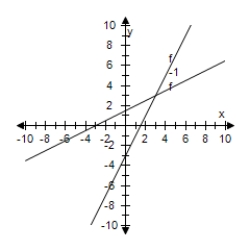
B)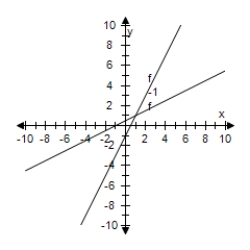
C)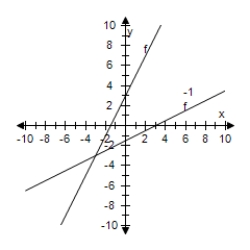
D)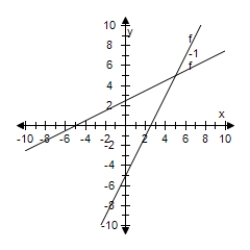
E)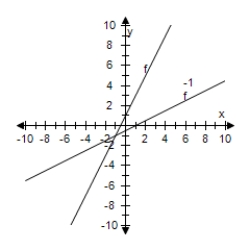
F(x) = 2x - 3
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
9
Select the graph of the function, and use the Horizontal Line Test to determine whether the function is one-to-one and so has an inverse function.
A)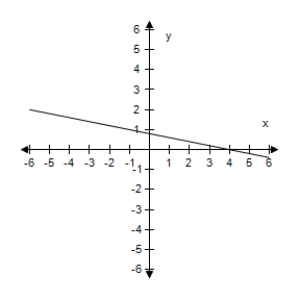 The function has an inverse.
The function has an inverse.
B)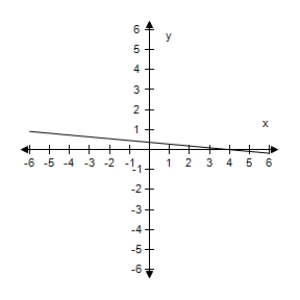 The function has an inverse.
The function has an inverse.
C)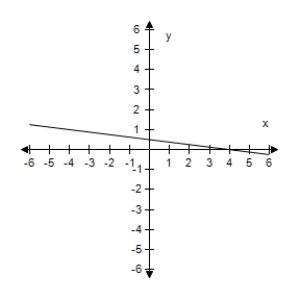 The function has an inverse.
The function has an inverse.
D)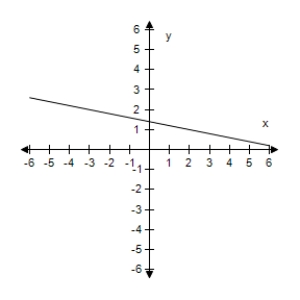 The function has an inverse.
The function has an inverse.
E)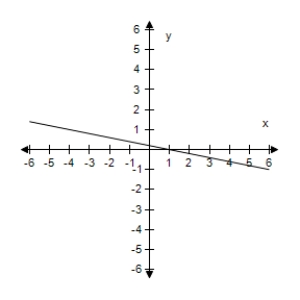 The function has an inverse.
The function has an inverse.
A)
 The function has an inverse.
The function has an inverse.B)
 The function has an inverse.
The function has an inverse.C)
 The function has an inverse.
The function has an inverse.D)
 The function has an inverse.
The function has an inverse.E)
 The function has an inverse.
The function has an inverse.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
10
Select the correct graph, showing f and g are inverse functions.
A)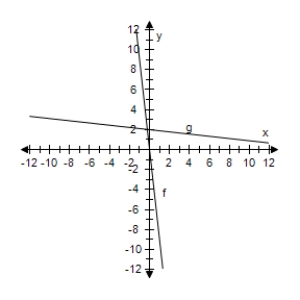
B)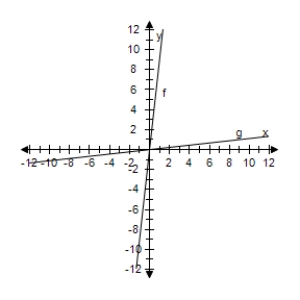
C)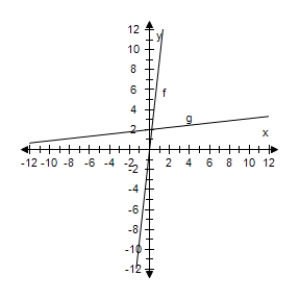
D)
E)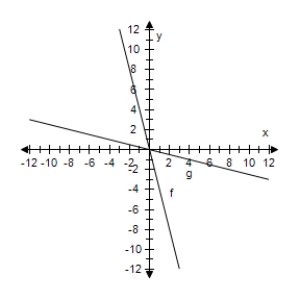
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
11
Select the graph of f and f-1 on the same set of coordinate axes.
A)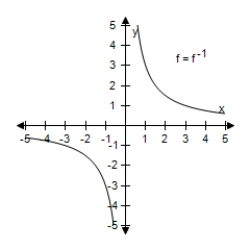
B)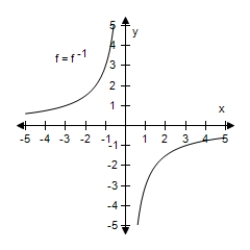
C)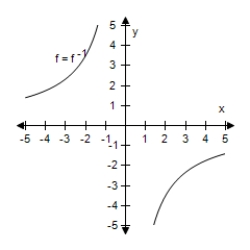
D)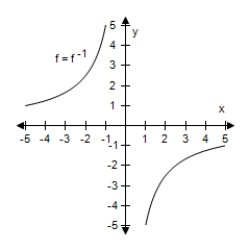
E)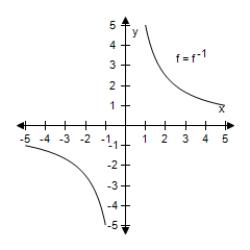
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
12
Select the correct graph, showing f and g are inverse functions.
A)![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa8_d5b7_a6c3_1359b8da9de2_TB7698_11.jpg)
B)![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa8_fcc8_a6c3_d9dc4956d353_TB7698_11.jpg)
C)![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_23d9_a6c3_47f3ca21e23a_TB7698_11.jpg)
D)![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_23da_a6c3_bf9137d0c205_TB7698_11.jpg)
E)![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_4aeb_a6c3_a53289852e67_TB7698_11.jpg)
A)
![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa8_d5b7_a6c3_1359b8da9de2_TB7698_11.jpg)
B)
![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa8_fcc8_a6c3_d9dc4956d353_TB7698_11.jpg)
C)
![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_23d9_a6c3_47f3ca21e23a_TB7698_11.jpg)
D)
![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_23da_a6c3_bf9137d0c205_TB7698_11.jpg)
E)
![<strong>Select the correct graph, showing f and g are inverse functions. f ( x ) = \frac { x ^ { 3 } } { 7 } , g ( x ) = \sqrt [ 3 ] { 7 x } </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB7698/11eae838_9aa9_4aeb_a6c3_a53289852e67_TB7698_11.jpg)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find the inverse function of g(x) = x2 - 3 informally.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
14
Find the inverse function of f informally.
F(x) = x4
A)
B)
C)
D)
E)
F(x) = x4
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
15
Find the inverse function of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
16
Select the correct graph, showing f and g are inverse functions.
A)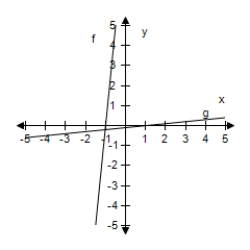
B)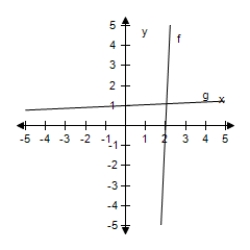
C)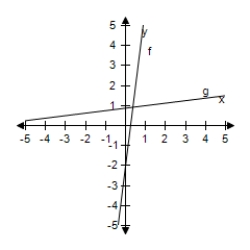
D)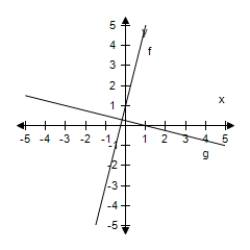
E)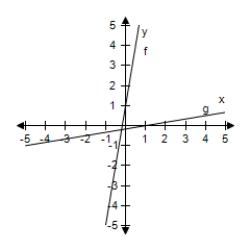
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
17
Determine whether the function has an inverse function.If it does, find the inverse function.
G(x) = x7
A)
B)g-1(x) = -7x
C)
D)g-1(x) = 7x
E)The inverse exists, but none of the above
G(x) = x7
A)
B)g-1(x) = -7x
C)
D)g-1(x) = 7x
E)The inverse exists, but none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
18
Does the function have an inverse function? 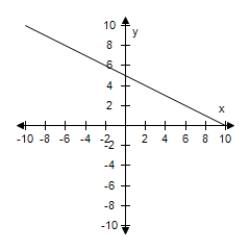


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
19
Find the inverse function of f informally.
F(x) = 6x
A)f-1(x) = 6 - x
B)f-1(x) = 6 + x
C)
D)f-1(x) = x - 6
E)f(x) = 6x
F(x) = 6x
A)f-1(x) = 6 - x
B)f-1(x) = 6 + x
C)
D)f-1(x) = x - 6
E)f(x) = 6x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
20
Select the correct graph, showing f and g are inverse functions.
A)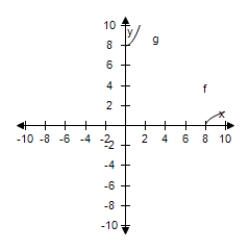
B)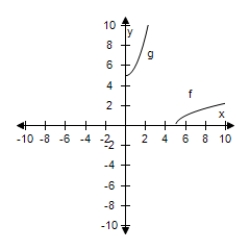
C)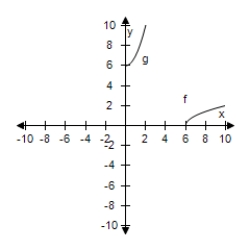
D)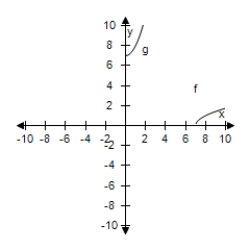
E)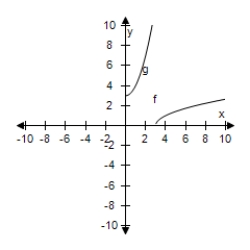
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
21
Determine whether the function has an inverse function.If it does, find the inverse function.
F(x) = (x + 4)2, x -4
A)
B)f-1(x) = -(x + 4)2
C)f-1(x) = (x + 4)-2
D)
E)No inverse
F(x) = (x + 4)2, x -4
A)
B)f-1(x) = -(x + 4)2
C)f-1(x) = (x + 4)-2
D)
E)No inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
22
Restrict the domain of the function f so that the function is one-to-one and has an inverse function.Then find the inverse function f-1.State the domains and ranges of f and f-1.
F(x) = -6x2 + 2
A) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
B) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
C) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
D) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x -2.
E) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
F(x) = -6x2 + 2
A) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
B) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
C) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.
D) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x -2.
E) The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 2.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
23
Restrict the domain of the function f so that the function is one-to-one and has an inverse function.Then find the inverse function f-1.State the domains and ranges of f and f-1.
F(x) = |x - 9| + 1
A)f-1(x) = x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
B)f-1(x) = x - 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
C)f-1(x) = -x - 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 1.The domain of f-1 and the range of f are all real numbers x such that x ≥ -9.
D)f-1(x) = x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ -9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
E)f-1(x) = -x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 1.The domain of f-1 and the range of f are all real numbers x such that x ≥ 9.
F(x) = |x - 9| + 1
A)f-1(x) = x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
B)f-1(x) = x - 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
C)f-1(x) = -x - 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 1.The domain of f-1 and the range of f are all real numbers x such that x ≥ -9.
D)f-1(x) = x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ -9.The domain of f-1 and the range of f are all real numbers x such that x ≥ 1.
E)f-1(x) = -x + 8The domain of f and the range of f-1 are all real numbers x such that x ≥ 1.The domain of f-1 and the range of f are all real numbers x such that x ≥ 9.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
24
Determine whether the function has an inverse function.If it does, find the inverse function.
F(x) = -2
A)f-1(x) = 2
B)
C)
D)f-1(x) = -2
E)No inverse
F(x) = -2
A)f-1(x) = 2
B)
C)
D)f-1(x) = -2
E)No inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
25
Use the functions given by and g(x) = x3 to find (g-1 º f-1)(-5).
A)-2
B)0
C)-4
D)2
E)4
A)-2
B)0
C)-4
D)2
E)4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
26
Restrict the domain of f(x) = x2 + 5 to x ≥ 0.Use a graphing utility to graph the function.
A)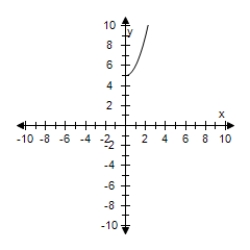
B)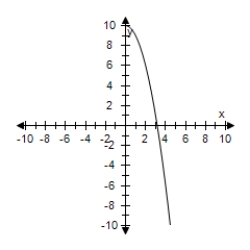
C)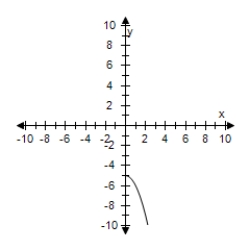
D)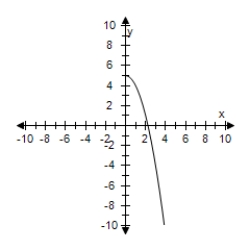
E)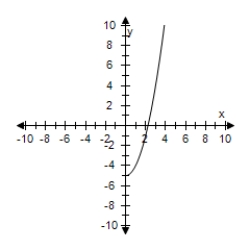
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
27
Restrict the domain of the function f so that the function is one-to-one and has an inverse function.Then find the inverse function f-1.State the domains and ranges of f and f-1.
F(x) = (x - 5)2
A)
The domain of f and the range of f-1 are all real numbers x such that x 5.The domain of f-1 and the range of f are all real numbers x such that x 0.
B)
The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x -5.
C)
The domain of f and the range of f-1 are all real numbers x such that x 5.The domain of f-1 and the range of f are all real numbers x such that x 0.
D)
The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 5.
E)
The domain of f and the range of f-1 are all real numbers x such that x -5.The domain of f-1 and the range of f are all real numbers x such that x 0.
F(x) = (x - 5)2
A)
The domain of f and the range of f-1 are all real numbers x such that x 5.The domain of f-1 and the range of f are all real numbers x such that x 0.
B)
The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x -5.
C)
The domain of f and the range of f-1 are all real numbers x such that x 5.The domain of f-1 and the range of f are all real numbers x such that x 0.
D)
The domain of f and the range of f-1 are all real numbers x such that x 0.The domain of f-1 and the range of f are all real numbers x such that x 5.
E)
The domain of f and the range of f-1 are all real numbers x such that x -5.The domain of f-1 and the range of f are all real numbers x such that x 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
28
Restrict the domain of the function f so that the function is one-to-one and has an inverse function.Then find the inverse function f-1.State the domains and ranges of f and f-1.
F(x) = |x + 5|
A)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ -5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.
B)f-1(x) = x + 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 0.The domain of f-1 and the range of f are all real numbers x such that x ≥ -5.
C)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 0.The domain of f-1 and the range of f are all real numbers x such that x ≥ 5.
D)f-1(x) = x + 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.
E)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.
F(x) = |x + 5|
A)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ -5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.
B)f-1(x) = x + 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 0.The domain of f-1 and the range of f are all real numbers x such that x ≥ -5.
C)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 0.The domain of f-1 and the range of f are all real numbers x such that x ≥ 5.
D)f-1(x) = x + 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.
E)f-1(x) = x - 5The domain of f and the range of f-1 are all real numbers x such that x ≥ 5.The domain of f-1 and the range of f are all real numbers x such that x ≥ 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
29
Use the functions given by and g(x) = x3 to find (f-1 º g-1)(1).
A)14
B)12
C)16
D)20
E)18
A)14
B)12
C)16
D)20
E)18

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
30
Use the functions given by and g(x) = x3 to find (f º g)-1.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
31
The function given by y = 0.03x2 + 245.50, 0 < x < 100 approximates the exhaust temperature y in degrees Fahrenheit, x where is the percent load for a diesel engine.Find the inverse function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
32
Use the functions given by f(x) = x + 2 and g(x) = 2x - 5 to find (f º g)-1.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
33
Your wage is $11.00 per hour plus $0.50 for each unit produced per hour.So, your hourly wage in terms of the number of units produced x is y = 11 + 0.50x.Find the inverse function.What does each variable represent in the inverse function
A) x = hourly wage; y = numbers of units produced
B)y = 11 + 0.50xx = hourly wage; y = numbers of units produced
C) x = hourly wage; y = numbers of units produced
D) x = hourly wage; y = numbers of units produced
E)y = 11 - 0.50xx = hourly wage; y = numbers of units produced
A) x = hourly wage; y = numbers of units produced
B)y = 11 + 0.50xx = hourly wage; y = numbers of units produced
C) x = hourly wage; y = numbers of units produced
D) x = hourly wage; y = numbers of units produced
E)y = 11 - 0.50xx = hourly wage; y = numbers of units produced

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
34
Determine whether the function has an inverse function.If it does, find the inverse function.
A)
B) .
C)
D)
E)No inverse
A)
B) .
C)
D)
E)No inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
35
Use the graph of the function f to create a table of values for the given points.Then create a second table that can be used to find f-1.
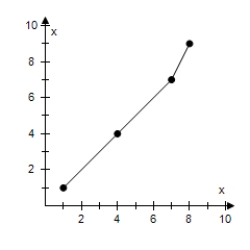
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
36
Determine whether the function has an inverse function.If it does, find the inverse function.
A)
B)
C)
D)
E)No inverse
A)
B)
C)
D)
E)No inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
37
Use the functions given by and g(x) = x3 to find (f-1 º f-1)(-5).
A)36
B)44
C)40
D)38
E)42
A)36
B)44
C)40
D)38
E)42

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
38
Use the functions given by f(x) = x + 6 and g(x) = 7x - 3 to find g-1 º f-1.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
39
Use the functions given by and g(x) = x3 to find g-1 º f-1.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
40
Determine whether the function has an inverse function.If it does, find the inverse function.
A)
B)
C)
D)
E)No Inverse
A)
B)
C)
D)
E)No Inverse

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find the inverse of the one-to-one function.
y = 5x + 4
f -1(x) = __________
y = 5x + 4
f -1(x) = __________

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find the inverse of the one-to-one function.
A)
B)
C)
D)
E)inverse does not exist
A)
B)
C)
D)
E)inverse does not exist

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
43
Determine algebraically whether f and g are inverse functions. f(x) = 5x - 3
A)Yes, f and g are inverse functions.
B)No, f and g are not inverse functions.
A)Yes, f and g are inverse functions.
B)No, f and g are not inverse functions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
44
Graph the given function. f(x) = (x - 3)2 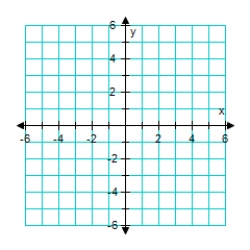
A)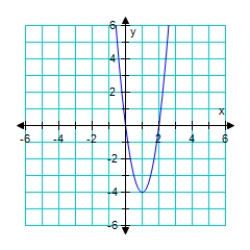
B)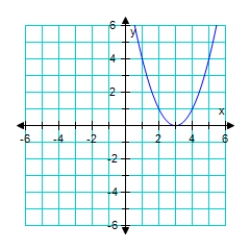
C)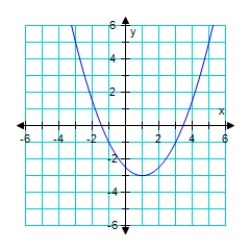
D)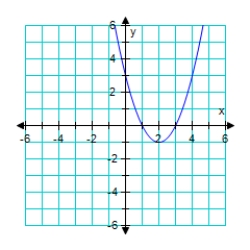
E)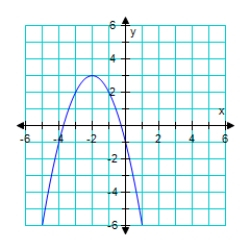

A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
45
Determine whether the function has an inverse function.If it does, find the inverse function.
A)
B)
C)
D)
E)No inverse function exists.
A)
B)
C)
D)
E)No inverse function exists.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
46
The function f(x) = x2 - 2 is one-to-one on the domain (x 0) .Find f -1(x).
A)
B)
C)
D)
E)f -1(x) = x2 + 2
A)
B)
C)
D)
E)f -1(x) = x2 + 2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find (f + g)(x).
A)2x
B)4x
C)-4x
D)-2x
E)2x + 8
A)2x
B)4x
C)-4x
D)-2x
E)2x + 8

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find (f + g)(x).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
49
Determine whether the function is one-to- one.
Y = 3x
A)No, it isn't one-to-one.
B)Yes, it is one-to-one.
Y = 3x
A)No, it isn't one-to-one.
B)Yes, it is one-to-one.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find (f - g)(x).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
51
Determine whether the function has an inverse function.If it does, find the inverse function. f(x) = x2 + 5
A)
B)
C)
D)
E)No inverse function exists.
A)
B)
C)
D)
E)No inverse function exists.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
52
Find the inverse of the one-to-one function.
Y = 3x
A)
B)f -1(x) = 3x
C)
D)
E)f -1(x) = 9x
Y = 3x
A)
B)f -1(x) = 3x
C)
D)
E)f -1(x) = 9x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
53
Use the functions given by and g(x) = x3 to find the indicated value. (f º g)-1(5)
A)
B)
C)
D)
E) Undefined
A)
B)
C)
D)
E) Undefined

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
54
Find (f - g)(x).
A)2x - 6
B)6
C)2x - 3
D)2x + 6
E)2x
A)2x - 6
B)6
C)2x - 3
D)2x + 6
E)2x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
55
Find the inverse of the one-to-one function.
Y = 5x + 9
A)
B)
C)
D)
E)none of the above
Y = 5x + 9
A)
B)
C)
D)
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the inverse of the one-to-one function.
y = 6x
f -1(x) = __________
y = 6x
f -1(x) = __________

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
57
Determine algebraically whether f and g are inverse functions. g(x) = x2 - 6, x 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
58
Find the inverse of the one-to-one function.
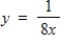
f -1(x) = __________
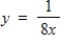
f -1(x) = __________

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
59
Show algebraically that f and g are inverse functions.
f(x) = 9x + 9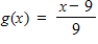
f(x) = 9x + 9
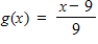

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
60
Determine whether the function is one-to-one.
Y = (x - 5)2; x ≥ 5
A)No, it isn't one-to-one.
B)Yes, it is one-to-one.
Y = (x - 5)2; x ≥ 5
A)No, it isn't one-to-one.
B)Yes, it is one-to-one.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
61
Evaluate the indicated function for and .
A)30
B)
C)
D)
E)
A)30
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
62
Find and the domain of the composite function.
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
63
Evaluate the indicated function for and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
64
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
65
Evaluate the indicated function for and .
A)28
B)38
C)-38
D)125
E)17
A)28
B)38
C)-38
D)125
E)17

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
67
Evaluate the indicated function for and .
A)92
B)90
C)-86
D)89
E)91
A)92
B)90
C)-86
D)89
E)91

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
68
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
69
Find (f + g)(x).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
70
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find and the domain of the composite function.
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find (f / g)(x).What is the domain of f / g
A) ; all real numbers x.
B) ; all real numbers x except x = 0
C) ; all real numbers x except x =
D) ; all real numbers x except x = 0
E) ; all real numbers x except x =
A) ; all real numbers x.
B) ; all real numbers x except x = 0
C) ; all real numbers x except x =
D) ; all real numbers x except x = 0
E) ; all real numbers x except x =

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
73
Find (fg)(x).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
74
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find and the domain of the composite function.
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
76
Evaluate the indicated function for and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
77
Find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
78
Find and the domain of the composite function.
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x
A) Domain of : all real numbers x
B) Domain of : all real numbers x
C) Domain of : all real numbers x
D) Domain of : all real numbers x
E) Domain of : all real numbers x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
79
Evaluate the indicated function for and .
A)12
B)-10
C)7
D)14
E)10
A)12
B)-10
C)7
D)14
E)10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck
80
Evaluate the indicated function for and .
A)48
B)39
C)9
D)0
E)-39
A)48
B)39
C)9
D)0
E)-39

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 513 في هذه المجموعة.
فتح الحزمة
k this deck








