Deck 11: Techniques of Differentiation
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/104
العب
ملء الشاشة (f)
Deck 11: Techniques of Differentiation
1
Find using implicit differentiation. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Find using implicit differentiation. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Find using implicit differentiation. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Use logarithmic differentiation to find . ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
5
Use logarithmic differentiation to find 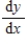 .
.
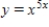
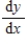 .
.
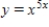

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
7
The number P of CDs the Snappy Hardware Co. can manufacture at its plant in one day is given by
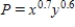
where x is the number of workers at the plant and y is the annual expenditure at the plant (in dollars). Compute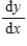 at a production level of 23,000 CDs per day and
at a production level of 23,000 CDs per day and 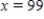 . Round your answer to two decimal places.
. Round your answer to two decimal places.
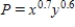
where x is the number of workers at the plant and y is the annual expenditure at the plant (in dollars). Compute
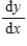 at a production level of 23,000 CDs per day and
at a production level of 23,000 CDs per day and 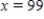 . Round your answer to two decimal places.
. Round your answer to two decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
8
Find the equation of the tangent line for at the point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
9
The number P of CDs the Snappy Hardware Co. can manufacture at its plant in one day is given by
Where x is the number of workers at the plant and y is the annual expenditure at the plant (in dollars). Compute at a production level of 24,000 CDs per day and . Round your answer to two decimal places.
A)-250.64
B) -234.31
C) -222.19
D) -255.85
E) 234.31
Where x is the number of workers at the plant and y is the annual expenditure at the plant (in dollars). Compute at a production level of 24,000 CDs per day and . Round your answer to two decimal places.
A)-250.64
B) -234.31
C) -222.19
D) -255.85
E) 234.31

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
12
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
14
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
15
An employment research company estimates that the value of a recent MBA graduate to an accounting company is
Where V is the value of the graduate, ?e is a number of years of prior business experience, and g is the graduate school grade point average. If
, find when .
All the answers were rounded to the nearest hundredth.
A)0.13
B) -1.58
C) -2.79
D) -0.13
E) -0.25
Where V is the value of the graduate, ?e is a number of years of prior business experience, and g is the graduate school grade point average. If
, find when .
All the answers were rounded to the nearest hundredth.
A)0.13
B) -1.58
C) -2.79
D) -0.13
E) -0.25

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
16
Use logarithmic differentiation to find . Do not simplify the result.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find the derivative of the following function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
18
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
19
Find using implicit differentiation. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find using implicit differentiation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
21
Find the derivative of the following function.
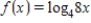
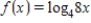

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
22
Find the derivative of the following function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
23
If $17,000 is invested in a savings account yielding 3% per year, compounded semiannually, how fast is the balance growing after 3 years Round your answer to the nearest cent.
A)$691.89 per year
B) $387.46 per year
C) $774.92 per year
D) $996.33 per year
E) $553.52 per year
A)$691.89 per year
B) $387.46 per year
C) $774.92 per year
D) $996.33 per year
E) $553.52 per year

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
24
Calculate the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
25
Find the equation of the straight line, tangent to at the point .
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
27
The population of Upper Anchora was 1,000,000 at the start of 1996 and was doubling every 9 years. How fast was it growing per year at the start of 1996 ?
Round your answer to the nearest thousand.
A)154,000 people per year
B) 78,000 people per year
C) 77,000 people per year
D) 76,000 people per year
E) 67,000 people per year
Round your answer to the nearest thousand.
A)154,000 people per year
B) 78,000 people per year
C) 77,000 people per year
D) 76,000 people per year
E) 67,000 people per year

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
28
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
29
Find the indicated derivative. The independent variable is a function of t.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
31
Find the derivative of the function.
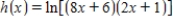
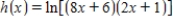

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
32
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
33
If $24,000 is invested in a savings account yielding 6% per year, compounded semiannually, how fast is the balance growing after 2 years
Please enter your answer as a number (in $ per year) without the units. Round your answer to two decimal places.
Please enter your answer as a number (in $ per year) without the units. Round your answer to two decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
34
Calculate the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
36
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
38
Find the derivative of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
39
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
40
Find the derivative of the function.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find the derivative of the function.
A)
B)
C) 4
D)
E)
A)
B)
C) 4
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
42
Calculate . You need not expand your answer.
A)
B)
C)
D)
E) 0.5
A)
B)
C)
D)
E) 0.5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the derivative of the function.
A)
B)
C) 4
D)
E)
A)
B)
C) 4
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
44
The demand for the Cyberpunk II arcade video game is modeled by the logistic curve
Where is the total number of units sold t months after the game's introduction.
Use technology to estimate .
Assume that the manufacturers of Cyberpunk II sell each unit for $900. What is the company's marginal revenue,
Use the chain rule to estimate the rate at which revenue is growing 9 months after the introduction of the video game.
Please round each answer to the nearest whole number.
A)
B)
C)
D)
E)
Where is the total number of units sold t months after the game's introduction.
Use technology to estimate .
Assume that the manufacturers of Cyberpunk II sell each unit for $900. What is the company's marginal revenue,
Use the chain rule to estimate the rate at which revenue is growing 9 months after the introduction of the video game.
Please round each answer to the nearest whole number.
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
45
The Pentagon is planning to build a new satellite that will be spherical. As is typical in these cases, the specifications keep changing, so that the size of the satellite keeps growing. In fact, the radius of the planned satellite is growing 0.9 foot/week. Its cost will be $1,400 per cubic foot. At the point when the plans call for a satellite 8 feet in radius, how fast is the cost growing (The volume of a solid sphere of radius r is .)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
46
Compute the indicated derivative using the chain rule.
A)
B)
C)
D) 7
E) -10
A)
B)
C)
D) 7
E) -10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
47
Calculate .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
48
Compute the indicated derivative using the chain rule. ;
A)
B) 6
C) 7
D)
E)
A)
B) 6
C) 7
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
49
Compute the indicated derivative using the chain rule.
A)
B)
C)
D) 2
E)
A)
B)
C)
D) 2
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
50
Calculate the derivative of the function.
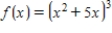
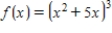

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
51
Find the indicated derivative. , when , ;
Please round the answer to the nearest hundredth.
A)
B)
C)
D)
E)
Please round the answer to the nearest hundredth.
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
52
Calculate the derivative of the function.
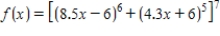
Please enter your answer as an expression.
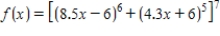
Please enter your answer as an expression.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
53
Calculate . You need not expand your answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
54
Calculate . You need not expand your answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
55
Find the indicated derivative. ? , when , ;
Please round the answer to the nearest hundredth.
A)
B)
C)
D)
E)
Please round the answer to the nearest hundredth.
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the derivative of the function.
A)
B) 5
C) 4
D)
E)
A)
B) 5
C) 4
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
57
A mold culture in a dorm refrigerator is circular and growing. The radius is increasing at a rate of 0.1 cm/day. How fast is the area growing when the culture is 6 centimeters in radius (The area of a disc of radius r is .)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
58
An offshore oil well is leaking oil and creating a circular oil slick. If the radius of the slick is growing at a rate of 7 miles per hour, find the rate at which the area is increasing when the radius is 3 miles. (The area of a disc of radius r is .)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
59
The soap bubble I am blowing has a radius that is growing at a rate of 3 cm/s. How fast is the surface area growing when the radius is 10 cm (The surface area of a sphere of radius r is .)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
60
Calculate . You need not expand your answer. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
61
The monthly sales of Sunny Electronics' new stereo system is given by 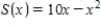 hundred units per month, x months after its introduction. The price Sunny charges is
hundred units per month, x months after its introduction. The price Sunny charges is 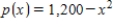 dollars per stereo system, x months after its introduction. The revenue Sunny earns then must be
dollars per stereo system, x months after its introduction. The revenue Sunny earns then must be 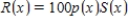 . Find the rate of change of revenue 10 months after introduction.
. Find the rate of change of revenue 10 months after introduction.
Please enter your answer in dollars/month without the units.
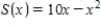 hundred units per month, x months after its introduction. The price Sunny charges is
hundred units per month, x months after its introduction. The price Sunny charges is 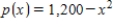 dollars per stereo system, x months after its introduction. The revenue Sunny earns then must be
dollars per stereo system, x months after its introduction. The revenue Sunny earns then must be 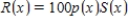 . Find the rate of change of revenue 10 months after introduction.
. Find the rate of change of revenue 10 months after introduction.
Please enter your answer in dollars/month without the units.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
62
The monthly sales of Sunny Electronics' new stereo system is given by hundred units per month, x months after its introduction. The price Sunny charges is dollars per stereo system, x months after its introduction. The revenue Sunny earns then must be . Find the rate of change of revenue 6 months after introduction. Round your answer to the nearest dollar.
A)$437,700 per month
B) $43,770 per month
C) $1,562,400 per month
D) -$391,800 per month
E) -$322,700 per month
A)$437,700 per month
B) $43,770 per month
C) $1,562,400 per month
D) -$391,800 per month
E) -$322,700 per month

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
63
The "Verhulst model" for population growth specifies the reproductive rate of an organism as a function of the total population according to the following formula: ?
Where p is the total population in thousands of organisms, r and k are constants that depend on the particular circumstances and organism being studied, and R(p) is the reproduction rate in thousands of organisms per hour. If and , find .
A)
B)
C)
D)
E)
Where p is the total population in thousands of organisms, r and k are constants that depend on the particular circumstances and organism being studied, and R(p) is the reproduction rate in thousands of organisms per hour. If and , find .
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
64
For the cost function C(x), find the marginal cost at the given production level x. Round your answer to two decimal places.
A)$19.62 per item
B) $21.28 per item
C) $9.61 per item
D) $19.60 per item
E) $15.00 per item
A)$19.62 per item
B) $21.28 per item
C) $9.61 per item
D) $19.60 per item
E) $15.00 per item

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
65
Calculate . You need not expand your answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
66
Your monthly profit (in dollars) from selling magazines is given by where x is the number of magazines you sell in a month. If you are currently selling magazines per month, find your profit and your marginal profit.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
67
Find the equation of the tangent line to the graph of the given function at the point with .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
68
The Thoroughbred Bus Company finds that its monthly costs for one particular year were given by dollars after t months. After t months, the company had passengers per month. How fast was its cost per passenger changing after 6 months
Enter your answer in dollars/month rounded to the nearest cent and without the units.
Enter your answer in dollars/month rounded to the nearest cent and without the units.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
69
For the cost function, find the marginal cost at the given production level x. Round your answer to two decimal places.
A)$9.60 per item
B) $9.58 per item
C) $10.00 per item
D) $9.61 per item
E) $10.40 per item
A)$9.60 per item
B) $9.58 per item
C) $10.00 per item
D) $9.61 per item
E) $10.40 per item

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
70
Calculate . You need not expand your answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
71
The Thoroughbred Bus Company finds that its monthly costs for one particular year were given by dollars after t months. After t months, the company had passengers per month. How fast was its cost per passenger changing after 4 months Round your answer to the nearest cent.
A)$0.29 per month
B) $0.01 per month
C) -$0.21 per month
D) $0.46 per month
E) $0.07 per month
A)$0.29 per month
B) $0.01 per month
C) -$0.21 per month
D) $0.46 per month
E) $0.07 per month

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find the equation of the line tangent to the graph of the given function at the point 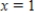 .
.
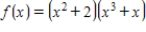
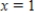 .
.
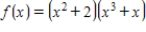

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
73
Compute the derivative. ?
A)3
B) 0
C) 1
D) 7
E) -1
A)3
B) 0
C) 1
D) 7
E) -1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
74
Your Porche's gas mileage (in miles per gallon) is given as a function M(x) of speed x in miles per hour.
Calculate .
A)
B)
C)
D) ?
E)
Calculate .
A)
B)
C)
D) ?
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find the equation of the line tangent to the graph of the given function at the point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
76
Calculate . You need not expand your answer.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
77
The cost, in thousands of dollars, of airing x television commercials during a Super Bowl game is given by the formula
.
Estimate how fast (in dollars per television commercial) the cost is going up when .
A)$1,200,080
B) $1,199,920
C) $1,199.92
D) $1,199,960
E) $1,200
.
Estimate how fast (in dollars per television commercial) the cost is going up when .
A)$1,200,080
B) $1,199,920
C) $1,199.92
D) $1,199,960
E) $1,200

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
78
Compute the derivative.
A)-108
B) 132
C) 100
D) 131
E) 144
A)-108
B) 132
C) 100
D) 131
E) 144

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
79
The cost of producing x teddy bears per day at the Cuddly Companion Company is calculated by their marketing staff to be given by the formula
.
Evaluate the average cost .
A)$12,199.80
B) $59.80
C) $12,160.00
D) $59.20
E) $60.80
.
Evaluate the average cost .
A)$12,199.80
B) $59.80
C) $12,160.00
D) $59.20
E) $60.80

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck
80
Find the value of x for which the marginal profit is zero.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 104 في هذه المجموعة.
فتح الحزمة
k this deck








