Deck 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/56
العب
ملء الشاشة (f)
Deck 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution
1
Any change to the objective function coefficient of a variable that is positive in the optimal solution will change the optimal solution.
False
2
When the right-hand sides of two constraints are each increased by one unit, the objective function value will be adjusted by the sum of the constraints' dual prices.
False
3
If the optimal value of a decision variable is zero and its reduced cost is zero, this indicates that alternative optimal solutions exist.
True
4
In order to tell the impact of a change in a constraint coefficient, the change must be made and then the model resolved.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
5
Relevant costs should be reflected in the objective function, but sunk costs should not.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
6
The amount of a sunk cost will vary depending on the values of the decision variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
7
The dual price associated with a constraint is the change in the value of the solution per unit decrease in the right-hand side of the constraint.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
8
Decreasing the objective function coefficient of a variable to its lower limit will create a revised problem that is unbounded.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
9
Classical sensitivity analysis provides no information about changes resulting from a change in the coefficient of a variable in a constraint.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
10
The 100 percent rule can be applied to changes in both objective function coefficients and right-hand sides at the same time.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
11
If the range of feasibility for b1 is between 16 and 37, then if b1 = 22 the optimal solution will not change from the original optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
12
If the range of feasibility indicates that the original amount of a resource, which was 20, can increase by 5, then the amount of the resource can increase to 25.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
13
For a minimization problem, a positive dual price indicates the value of the objective function will increase.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
14
If the dual price for the right-hand side of a ≤ constraint is zero, there is no upper limit on its range of feasibility.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
15
There is a dual price for every decision variable in a model.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
16
The 100% Rule does not imply that the optimal solution will necessarily change if the percentage exceeds 100%.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
17
A negative dual price indicates that increasing the right-hand side of the associated constraint would be detrimental to the objective.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
18
The dual price for a percentage constraint provides a direct answer to questions about the effect of increases or decreases in that percentage.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
19
For any constraint, either its slack/surplus value must be zero or its dual price must be zero.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
20
The reduced cost for a positive decision variable is 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
21
Sensitivity analysis information in computer output is based on the assumption of
A) no coefficient changes.
B) one coefficient changes.
C) two coefficients change.
D) all coefficients change.
A) no coefficient changes.
B) one coefficient changes.
C) two coefficients change.
D) all coefficients change.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
22
The range of feasibility measures
A) the right-hand-side values for which the objective function value will not change.
B) the right-hand-side values for which the values of the decision variables will not change.
C) the right-hand-side values for which the dual prices will not change.
D) each of these choices are true.
A) the right-hand-side values for which the objective function value will not change.
B) the right-hand-side values for which the values of the decision variables will not change.
C) the right-hand-side values for which the dual prices will not change.
D) each of these choices are true.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
23
A section of output from The Management Scientist is shown here.  What will happen if the right-hand-side for constraint 2 increases by 200?
What will happen if the right-hand-side for constraint 2 increases by 200?
A) Nothing. The values of the decision variables, the dual prices, and the objective function will all remain the same.
B) The value of the objective function will change, but the values of the decision variables and the dual prices will remain the same.
C) The same decision variables will be positive, but their values, the objective function value, and the dual prices will change.
D) The problem will need to be resolved to find the new optimal solution and dual price.
 What will happen if the right-hand-side for constraint 2 increases by 200?
What will happen if the right-hand-side for constraint 2 increases by 200?A) Nothing. The values of the decision variables, the dual prices, and the objective function will all remain the same.
B) The value of the objective function will change, but the values of the decision variables and the dual prices will remain the same.
C) The same decision variables will be positive, but their values, the objective function value, and the dual prices will change.
D) The problem will need to be resolved to find the new optimal solution and dual price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
24
To solve a linear programming problem with thousands of variables and constraints
A) a personal computer can be used.
B) a mainframe computer is required.
C) the problem must be partitioned into subparts.
D) unique software would need to be developed.
A) a personal computer can be used.
B) a mainframe computer is required.
C) the problem must be partitioned into subparts.
D) unique software would need to be developed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
25
Sensitivity analysis is often referred to as
A) feasibility testing.
B) duality analysis.
C) alternative analysis.
D) postoptimality analysis.
A) feasibility testing.
B) duality analysis.
C) alternative analysis.
D) postoptimality analysis.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
26
Which of the following is not a question answered by standard sensitivity analysis information?
A) If the right-hand side value of a constraint changes, will the objective function value change?
B) Over what range can a constraint's right-hand side value without the constraint's dual price possibly changing?
C) By how much will the objective function value change if the right-hand side value of a constraint changes beyond the range of feasibility?
D) By how much will the objective function value change if a decision variable's coefficient in the objective function changes within the range of optimality?
A) If the right-hand side value of a constraint changes, will the objective function value change?
B) Over what range can a constraint's right-hand side value without the constraint's dual price possibly changing?
C) By how much will the objective function value change if the right-hand side value of a constraint changes beyond the range of feasibility?
D) By how much will the objective function value change if a decision variable's coefficient in the objective function changes within the range of optimality?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
27
A section of output from The Management Scientist is shown here. 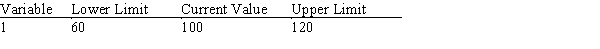 What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?
What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?
A) Nothing. The values of the decision variables, the dual prices, and the objective function will all remain the same.
B) The value of the objective function will change, but the values of the decision variables and the dual prices will remain the same.
C) The same decision variables will be positive, but their values, the objective function value, and the dual prices will change.
D) The problem will need to be resolved to find the new optimal solution and dual price.
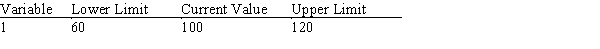 What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?
What will happen to the solution if the objective function coefficient for variable 1 decreases by 20?A) Nothing. The values of the decision variables, the dual prices, and the objective function will all remain the same.
B) The value of the objective function will change, but the values of the decision variables and the dual prices will remain the same.
C) The same decision variables will be positive, but their values, the objective function value, and the dual prices will change.
D) The problem will need to be resolved to find the new optimal solution and dual price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
28
The cost that varies depending on the values of the decision variables is a
A) reduced cost.
B) relevant cost.
C) sunk cost.
D) dual cost.
A) reduced cost.
B) relevant cost.
C) sunk cost.
D) dual cost.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
29
An objective function reflects the relevant cost of labor hours used in production rather than treating them as a sunk cost. The correct interpretation of the dual price associated with the labor hours constraint is
A) the maximum premium (say for overtime) over the normal price that the company would be willing to pay.
B) the upper limit on the total hourly wage the company would pay.
C) the reduction in hours that could be sustained before the solution would change.
D) the number of hours by which the right-hand side can change before there is a change in the solution point.
A) the maximum premium (say for overtime) over the normal price that the company would be willing to pay.
B) the upper limit on the total hourly wage the company would pay.
C) the reduction in hours that could be sustained before the solution would change.
D) the number of hours by which the right-hand side can change before there is a change in the solution point.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
30
A negative dual price for a constraint in a minimization problem means
A) as the right-hand side increases, the objective function value will increase.
B) as the right-hand side decreases, the objective function value will increase.
C) as the right-hand side increases, the objective function value will decrease.
D) as the right-hand side decreases, the objective function value will decrease.
A) as the right-hand side increases, the objective function value will increase.
B) as the right-hand side decreases, the objective function value will increase.
C) as the right-hand side increases, the objective function value will decrease.
D) as the right-hand side decreases, the objective function value will decrease.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
31
A constraint with a positive slack value
A) will have a positive dual price.
B) will have a negative dual price.
C) will have a dual price of zero.
D) has no restrictions for its dual price.
A) will have a positive dual price.
B) will have a negative dual price.
C) will have a dual price of zero.
D) has no restrictions for its dual price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
32
When the cost of a resource is sunk, then the dual price can be interpreted as the
A) minimum amount the firm should be willing to pay for one additional unit of the resource.
B) maximum amount the firm should be willing to pay for one additional unit of the resource.
C) minimum amount the firm should be willing to pay for multiple additional units of the resource.
D) maximum amount the firm should be willing to pay for multiple additional units of the resource.
A) minimum amount the firm should be willing to pay for one additional unit of the resource.
B) maximum amount the firm should be willing to pay for one additional unit of the resource.
C) minimum amount the firm should be willing to pay for multiple additional units of the resource.
D) maximum amount the firm should be willing to pay for multiple additional units of the resource.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
33
Sensitivity analysis is concerned with how certain changes affect
A) the feasible solution.
B) the unconstrained solution.
C) the optimal solution.
D) the degenerative solution.
A) the feasible solution.
B) the unconstrained solution.
C) the optimal solution.
D) the degenerative solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
34
The dual price for a < constraint
A) will always be < 0.
B) will always be > 0.
C) will be < 0 in a minimization problem and > 0 in a maximization problem.
D) will always equal 0.
A) will always be < 0.
B) will always be > 0.
C) will be < 0 in a minimization problem and > 0 in a maximization problem.
D) will always equal 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
35
If a decision variable is not positive in the optimal solution, its reduced cost is
A) what its objective function value would need to be before it could become positive.
B) the amount its objective function value would need to improve before it could become positive.
C) zero.
D) its dual price.
A) what its objective function value would need to be before it could become positive.
B) the amount its objective function value would need to improve before it could become positive.
C) zero.
D) its dual price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
36
The dual price measures, per unit increase in the right hand side of the constraint,
A) the increase in the value of the optimal solution.
B) the decrease in the value of the optimal solution.
C) the improvement in the value of the optimal solution.
D) the change in the value of the optimal solution.
A) the increase in the value of the optimal solution.
B) the decrease in the value of the optimal solution.
C) the improvement in the value of the optimal solution.
D) the change in the value of the optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
37
A cost that is incurred no matter what values the decision variables assume is
A) a reduced cost.
B) an optimal cost.
C) a sunk cost.
D) a dual cost.
A) a reduced cost.
B) an optimal cost.
C) a sunk cost.
D) a dual cost.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
38
The 100% Rule compares
A) proposed changes to allowed changes.
B) new values to original values.
C) objective function changes to right-hand side changes.
D) dual prices to reduced costs.
A) proposed changes to allowed changes.
B) new values to original values.
C) objective function changes to right-hand side changes.
D) dual prices to reduced costs.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
39
The amount the objective function coefficient of a decision variable would have to improve before that variable would have a positive value in the solution is the
A) dual price.
B) surplus variable.
C) reduced cost.
D) upper limit.
A) dual price.
B) surplus variable.
C) reduced cost.
D) upper limit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
40
The amount by which an objective function coefficient can change before a different set of values for the decision variables becomes optimal is the
A) optimal solution.
B) dual solution.
C) range of optimality.
D) range of feasibility.
A) optimal solution.
B) dual solution.
C) range of optimality.
D) range of feasibility.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
41
Use the following Management Scientist output to answer the questions.
LINEAR PROGRAMMING PROBLEM
MAX 31X1+35X2+32X3
S.T.
1) 3X1+5X2+2X3>90
2) 6X1+7X2+8X3<150
3) 5X1+3X2+3X3<120
OPTIMAL SOLUTION
Objective Function Value = 763.333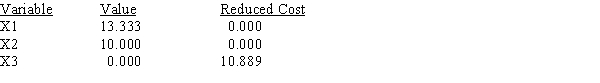
 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES 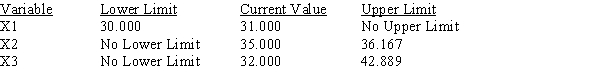 RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 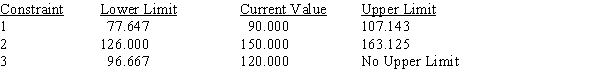
a.Give the solution to the problem.
b.Which constraints are binding?
c.What would happen if the coefficient of x1 increased by 3?
d.What would happen if the right-hand side of constraint 1 increased by 10?
LINEAR PROGRAMMING PROBLEM
MAX 31X1+35X2+32X3
S.T.
1) 3X1+5X2+2X3>90
2) 6X1+7X2+8X3<150
3) 5X1+3X2+3X3<120
OPTIMAL SOLUTION
Objective Function Value = 763.333
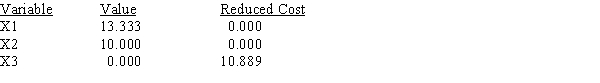
 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES 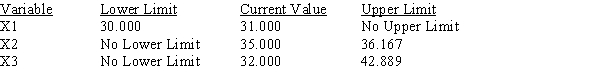 RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 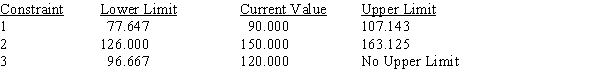
a.Give the solution to the problem.
b.Which constraints are binding?
c.What would happen if the coefficient of x1 increased by 3?
d.What would happen if the right-hand side of constraint 1 increased by 10?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
42
Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a minimization objective function and all ≥ constraints. 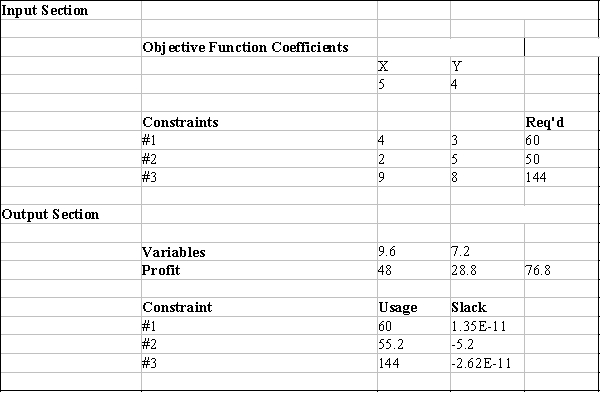
a.Give the original linear programming problem.
b.Give the complete optimal solution.

a.Give the original linear programming problem.
b.Give the complete optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
43
How can the interpretation of dual prices help provide an economic justification for new technology?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
44
Eight of the entries have been deleted from the LINDO output that follows. Use what you know about linear programming to find values for the blanks.
MIN 6 X1 + 7.5 X2 + 10 X3
SUBJECT TO
2) 25 X1 + 35 X2 + 30 X3 >= 2400
3) 2 X1 + 4 X2 + 8 X3 >= 400
END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 612.50000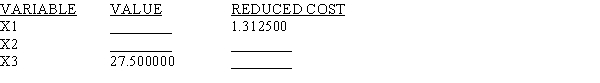
 NO. ITERATIONS= 2
NO. ITERATIONS= 2
RANGES IN WHICH THE BASIS IS UNCHANGED:

MIN 6 X1 + 7.5 X2 + 10 X3
SUBJECT TO
2) 25 X1 + 35 X2 + 30 X3 >= 2400
3) 2 X1 + 4 X2 + 8 X3 >= 400
END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 612.50000
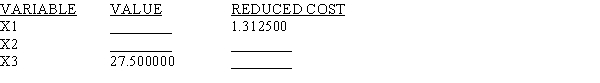
 NO. ITERATIONS= 2
NO. ITERATIONS= 2RANGES IN WHICH THE BASIS IS UNCHANGED:



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
45
In a linear programming problem, the binding constraints for the optimal solution are
5X + 3Y ≤ 30
2X + 5Y ≤ 20
a.Fill in the blanks in the following sentence:As long as the slope of the objective function stays between _______ and _______, the current optimal solution point will remain optimal.
b.Which of these objective functions will lead to the same optimal solution?1) 2X + 1Y 2) 7X + 8Y 3) 80X + 60Y 4) 25X + 35Y
5X + 3Y ≤ 30
2X + 5Y ≤ 20
a.Fill in the blanks in the following sentence:As long as the slope of the objective function stays between _______ and _______, the current optimal solution point will remain optimal.
b.Which of these objective functions will lead to the same optimal solution?1) 2X + 1Y 2) 7X + 8Y 3) 80X + 60Y 4) 25X + 35Y

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
46
Describe each of the sections of output that come from The Management Scientist and how you would use each.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
47
LINDO output is given for the following linear programming problem.
MIN 12 X1 + 10 X2 + 9 X3
SUBJECT TO
2) 5 X1 + 8 X2 + 5 X3 >= 60
3) 8 X1 + 10 X2 + 5 X3 >= 80
END
LP OPTIMUM FOUND AT STEP 1
OBJECTIVE FUNCTION VALUE
1) 80.000000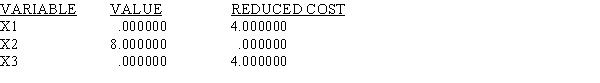
 NO. ITERATIONS= 1
NO. ITERATIONS= 1
RANGES IN WHICH THE BASIS IS UNCHANGED:

a.What is the solution to the problem?
b.Which constraints are binding?
c.Interpret the reduced cost for x1.
d.Interpret the dual price for constraint 2.
e.What would happen if the cost of x1 dropped to 10 and the cost of x2 increased to 12?
MIN 12 X1 + 10 X2 + 9 X3
SUBJECT TO
2) 5 X1 + 8 X2 + 5 X3 >= 60
3) 8 X1 + 10 X2 + 5 X3 >= 80
END
LP OPTIMUM FOUND AT STEP 1
OBJECTIVE FUNCTION VALUE
1) 80.000000
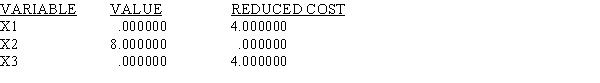
 NO. ITERATIONS= 1
NO. ITERATIONS= 1RANGES IN WHICH THE BASIS IS UNCHANGED:


a.What is the solution to the problem?
b.Which constraints are binding?
c.Interpret the reduced cost for x1.
d.Interpret the dual price for constraint 2.
e.What would happen if the cost of x1 dropped to 10 and the cost of x2 increased to 12?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
48
Portions of a Management Scientist output are shown below. Use what you know about the solution of linear programs to fill in the ten blanks.
LINEAR PROGRAMMING PROBLEM
MAX 12X1+9X2+7X3
S.T.
1) 3X1+5X2+4X3<150
2) 2X1+1X2+1X3<64
3) 1X1+2X2+1X3<80
4) 2X1+4X2+3X3>116
OPTIMAL SOLUTION
Objective Function Value = 336.000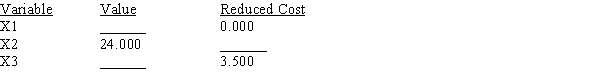
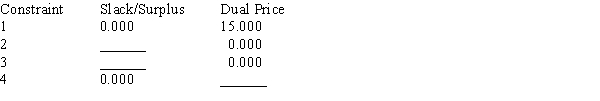 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES  RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 
LINEAR PROGRAMMING PROBLEM
MAX 12X1+9X2+7X3
S.T.
1) 3X1+5X2+4X3<150
2) 2X1+1X2+1X3<64
3) 1X1+2X2+1X3<80
4) 2X1+4X2+3X3>116
OPTIMAL SOLUTION
Objective Function Value = 336.000
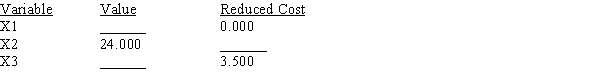
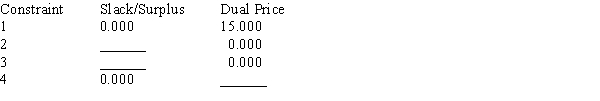 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES  RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
49
How would sensitivity analysis of a linear program be undertaken if one wishes to consider simultaneous changes for
both the right-hand-side values and objective function.
both the right-hand-side values and objective function.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
50
Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a maximization objective function and all ≤ constraints. 
a.Give the original linear programming problem.
b.Give the complete optimal solution.

a.Give the original linear programming problem.
b.Give the complete optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
51
Explain the two interpretations of dual prices based on the accounting assumptions made in calculating the objective
function coefficients.
function coefficients.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
52
The optimal solution of the linear programming problem is at the intersection of constraints 1 and 2.
Max
2x1 + x2
s.t.
4x1 + 1x2 ≤ 400
4x1 + 3x2 ≤ 600
1x1 + 2x2 ≤ 300
x1 , x2 ≥ 0
a.Over what range can the coefficient of x1 vary before the current solution is no longer optimal?
b.Over what range can the coefficient of x2 vary before the current solution is no longer optimal?
c.Compute the dual prices for the three constraints.
Max
2x1 + x2
s.t.
4x1 + 1x2 ≤ 400
4x1 + 3x2 ≤ 600
1x1 + 2x2 ≤ 300
x1 , x2 ≥ 0
a.Over what range can the coefficient of x1 vary before the current solution is no longer optimal?
b.Over what range can the coefficient of x2 vary before the current solution is no longer optimal?
c.Compute the dual prices for the three constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
53
The binding constraints for this problem are the first and second.
Min
x1 + 2x2
s.t.
x1 + x2 ≥ 300
2x1 + x2 ≥ 400
2x1 + 5x2 ≤ 750
x1 , x2 ≥ 0
a.Keeping c2 fixed at 2, over what range can c1 vary before there is a change in the optimal solution point?
b.Keeping c1 fixed at 1, over what range can c2 vary before there is a change in the optimal solution point?
c.If the objective function becomes Min 1.5x1 + 2x2, what will be the optimal values of x1, x2, and the objective function?
d.If the objective function becomes Min 7x1 + 6x2, what constraints will be binding?
e.Find the dual price for each constraint in the original problem.
Min
x1 + 2x2
s.t.
x1 + x2 ≥ 300
2x1 + x2 ≥ 400
2x1 + 5x2 ≤ 750
x1 , x2 ≥ 0
a.Keeping c2 fixed at 2, over what range can c1 vary before there is a change in the optimal solution point?
b.Keeping c1 fixed at 1, over what range can c2 vary before there is a change in the optimal solution point?
c.If the objective function becomes Min 1.5x1 + 2x2, what will be the optimal values of x1, x2, and the objective function?
d.If the objective function becomes Min 7x1 + 6x2, what constraints will be binding?
e.Find the dual price for each constraint in the original problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
54
How is sensitivity analysis used in linear programming? Given an example of what type of questions that can be
answered.
answered.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
55
Use the following Management Scientist output to answer the questions.
MIN 4X1+5X2+6X3
S.T.
1) X1+X2+X3<85
2) 3X1+4X2+2X3>280
3) 2X1+4X2+4X3>320
Objective Function Value = 400.000
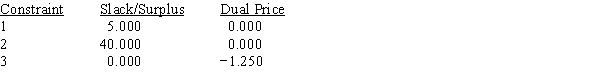 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES 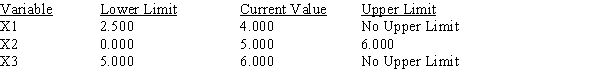 RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 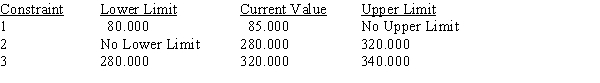
a.What is the optimal solution, and what is the value of the profit contribution?
b.Which constraints are binding?
c.What are the dual prices for each resource? Interpret.
d.Compute and interpret the ranges of optimality.
e.Compute and interpret the ranges of feasibility.
MIN 4X1+5X2+6X3
S.T.
1) X1+X2+X3<85
2) 3X1+4X2+2X3>280
3) 2X1+4X2+4X3>320
Objective Function Value = 400.000

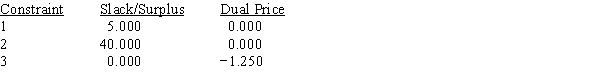 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES 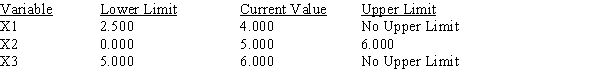 RIGHT HAND SIDE RANGES
RIGHT HAND SIDE RANGES 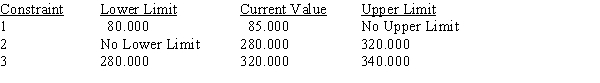
a.What is the optimal solution, and what is the value of the profit contribution?
b.Which constraints are binding?
c.What are the dual prices for each resource? Interpret.
d.Compute and interpret the ranges of optimality.
e.Compute and interpret the ranges of feasibility.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck
56
Explain the connection between reduced costs and the range of optimality, and between dual prices and the range of
feasibility.
feasibility.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 56 في هذه المجموعة.
فتح الحزمة
k this deck








