Deck 21: Parameters, Coordinates, Integrals
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/23
العب
ملء الشاشة (f)
Deck 21: Parameters, Coordinates, Integrals
1
Find parametric equations for the sphere 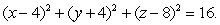
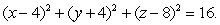
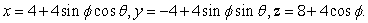
2
Find the parametric equation of the plane through the point (-4, 2, 4)and parallel to the lines and Select all that apply.
A)
B) .
C)
D)
E) ..
A)
B) .
C)
D)
E) ..
..
3
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (5, 0, 4).
Let P be the plane containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
In each case, give a parameterization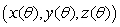 and specify the range of values your parameters must take on.
and specify the range of values your parameters must take on.
(i)the circle in which the cylinder, S, cuts the plane, P.
(ii)the surface of the cylinder S.
Let P be the plane containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
In each case, give a parameterization
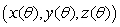 and specify the range of values your parameters must take on.
and specify the range of values your parameters must take on.(i)the circle in which the cylinder, S, cuts the plane, P.
(ii)the surface of the cylinder S.
(i) 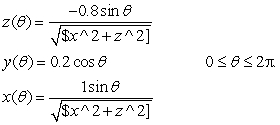
(ii)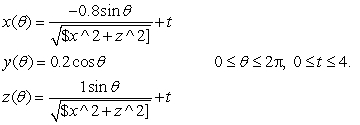
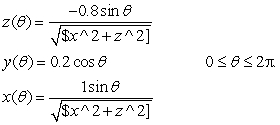
(ii)
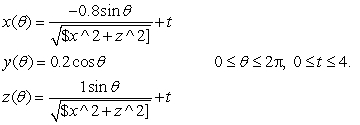
4
Consider the parametric surface Does it contain the point (0, -2, 0)?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
5
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (4, 0, 7).
Find two unit vectors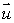 and
and 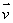 in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
Find two unit vectors
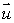 and
and 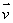 in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
6
Let R be the region in the first quadrant bounded between the circle 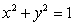 and the two axes.Then
and the two axes.Then 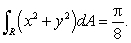 Let
Let 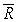 be the region in the first quadrant bounded between the ellipse
be the region in the first quadrant bounded between the ellipse 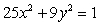 and the two axes.
and the two axes.
Use the change of variable x = s/5, y = t/3 to evaluate the integral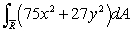
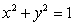 and the two axes.Then
and the two axes.Then 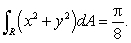 Let
Let 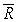 be the region in the first quadrant bounded between the ellipse
be the region in the first quadrant bounded between the ellipse 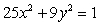 and the two axes.
and the two axes.Use the change of variable x = s/5, y = t/3 to evaluate the integral
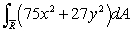

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
7
Consider the change of variables x = s + 3t, y = s - 2t.
Let R be the region bounded by the lines 2x + 3y = 1, 2x + 3y = 4, x - y = -3, and x - y = 2.Find the region T in the st-plane that corresponds to region R.
Use the change of variables to evaluate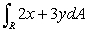 .
.
Let R be the region bounded by the lines 2x + 3y = 1, 2x + 3y = 4, x - y = -3, and x - y = 2.Find the region T in the st-plane that corresponds to region R.
Use the change of variables to evaluate
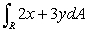 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
8
The following equations represent a curve or a surface.Select the best geometric description. (Note: , , are spherical coordinates; r, , z are cylindrical coordinates.)
A)Part of a line through the origin
B)Disk
C)Part of a cylinder.
D)Part of a cone.
A)Part of a line through the origin
B)Disk
C)Part of a cylinder.
D)Part of a cone.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
9
Find parametric equations for the cylinder
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
10
Let and Find a parametric equation for the plane through the point (1, 2, -1)and containing the vectors and Select all that apply.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
11
Consider the parametric surface Does it contain the x-axis?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
12
Let 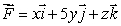 and S be parametric surface
and S be parametric surface 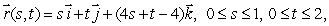 oriented upward.
oriented upward.
Use the formula for a flux integral over a parametric surface to find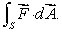 .
.
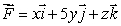 and S be parametric surface
and S be parametric surface 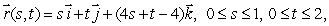 oriented upward.
oriented upward.Use the formula for a flux integral over a parametric surface to find
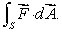 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
13
Let 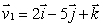 and
and 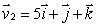 Find a vector which is perpendicular to
Find a vector which is perpendicular to 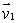 and
and 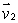 to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both
to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both 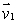 and
and 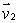 .Express your answer in the form
.Express your answer in the form 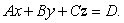
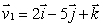 and
and 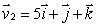 Find a vector which is perpendicular to
Find a vector which is perpendicular to 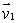 and
and 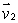 to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both
to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both 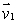 and
and 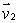 .Express your answer in the form
.Express your answer in the form 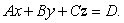

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
14
Consider the plane Does it contain the point (1, 6, -1)?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
15
Using cylindrical coordinates, find parametric equations for the cylinder Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
16
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (2, 0, 7).
Find the xyz-equation of the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
Find the xyz-equation of the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find parametric equations for the cylinder
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
18
Compute , where S is oriented in the positive direction and given, for 0 s 1, 0 t 2, by x = s, y = t2, z =8 t.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
19
Consider the plane Find a normal vector to the plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
20
Consider the change of variables x = s + 4t, y = s - 5t.
Find the absolute value of the Jacobian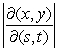 .
.
Find the absolute value of the Jacobian
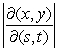 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
21
Let Find the flux of across the parametric surface S given by x = s cos t, y = s sin t, z = s, for 1 s 2, 0 t 2 , oriented downward.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
22
Compute the flux of the vector field over the surface S, which is oriented upward and given, for 0 s 1, 0 t 2 by

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck
23
Let Show that the parametric surface S given by x = s cos t, y = s sin t, z = s, for 1 s 2, 0 t 2 , oriented downward can also be written as the surface . Which of the following iterated integrals calculates the flux of across S? Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 23 في هذه المجموعة.
فتح الحزمة
k this deck








