Deck 9: Sequences and Series
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/70
العب
ملء الشاشة (f)
Deck 9: Sequences and Series
1
Determine whether the sequence converges or diverges.
A)It converges.
B)It diverges.
A)It converges.
B)It diverges.
It diverges.
2
A radioactive isotope is released into the air as an industrial by-product.This isotope is not very stable due to radioactive decay.Two-thirds of the original radioactive material loses its radioactivity after each month.If 13 grams of this isotope are released into the atmosphere at the end of the first and every subsequent month and the situation goes on ad infinitum, how many grams of radioactive material are in the atmosphere at the end of each month in the long run?
19.5
3
Stock prices for Abercrombie and Fitch fell steadily by an average of $0.94 per day from a high of $83.67 per share on December 24, 2007 to $70.05 on January 15, 2008.Let 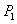 be the price of a share of stock on December 24, 2007.Write a formula for
be the price of a share of stock on December 24, 2007.Write a formula for 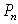 , the price of a share on the
, the price of a share on the 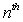 day after December 24.
day after December 24.
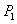 be the price of a share of stock on December 24, 2007.Write a formula for
be the price of a share of stock on December 24, 2007.Write a formula for 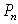 , the price of a share on the
, the price of a share on the 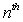 day after December 24.
day after December 24.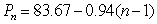
4
Let be the number of people visiting an amusement park on the nth day after it opens.Suppose .How many people visit the amusement park in its first week?
A)13888
B)13916
C)224
D)14000
A)13888
B)13916
C)224
D)14000

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
5
Let be the number of people visiting a zoo on the nth day after it opens.Suppose You find out that the museum must close if is has fewer than 300 visitors per day.How long will it remain open?
A)It will be closed on day 426.
B)It will be closed on day 501.
C)It will be closed on day 7.
D)It will close on day 1997.
A)It will be closed on day 426.
B)It will be closed on day 501.
C)It will be closed on day 7.
D)It will close on day 1997.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the value of 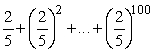 to 2 decimal places.
to 2 decimal places.
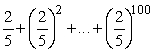 to 2 decimal places.
to 2 decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
7
A radioactive isotope is released into the air as an industrial by-product.This isotope is not very stable due to radioactive decay.Two-thirds of the original radioactive material loses its radioactivity after each month.If 15 grams of this isotope are released into the atmosphere at the end of the first and every subsequent month, how many grams of radioactive material are in the atmosphere at the end of the twelfth month? Round to 2 decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
8
Let be the number of people visiting an amusement park on the nth day after it opens.What does represent?
A)The average number of people visiting the amusement park over the first 10 days it was open.
B)The number of days it takes for 10 people to visit the amusement park.
C)The number of people visiting the amusement park on the 10th day after it opens.
D)The total number of people who have visited the amusement park the first 10 days it was open.
A)The average number of people visiting the amusement park over the first 10 days it was open.
B)The number of days it takes for 10 people to visit the amusement park.
C)The number of people visiting the amusement park on the 10th day after it opens.
D)The total number of people who have visited the amusement park the first 10 days it was open.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
9
Let be the number of people visiting a zoo on the nth day after it opens.What does represent?
A)The average number of people visiting the zoo over the first 25 days it was open.
B)The number of days it takes for 25 people to visit the zoo.
C)The number of people visiting the zoo on the 25th day it is open.
D)The total number of people who visited the zoo in the first 25 days after it opened.
A)The average number of people visiting the zoo over the first 25 days it was open.
B)The number of days it takes for 25 people to visit the zoo.
C)The number of people visiting the zoo on the 25th day it is open.
D)The total number of people who visited the zoo in the first 25 days after it opened.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find the value of the infinite product 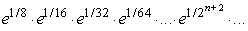 to 2 decimal places.
to 2 decimal places.
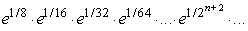 to 2 decimal places.
to 2 decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find a formula for , n 1, for the sequence
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
12
Let be the number of people visiting an aquarium on the nth day after it opens.What does it mean in terms of aquarium attendance if > for all n?
A)The number of people visiting the aquarium goes down each day.
B)The number of people visiting the aquarium goes up each day.
C)The number of people visiting the aquarium goes up some days and down some days.
A)The number of people visiting the aquarium goes down each day.
B)The number of people visiting the aquarium goes up each day.
C)The number of people visiting the aquarium goes up some days and down some days.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
13
Select the appropriate word to fill in the blank: A convergent sequence is ________________.
A)bounded
B)monotonic
C)finite
A)bounded
B)monotonic
C)finite

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
14
A couple puts $500,000 for their retirement into an account paying 5% annual interest.They estimate that they will need to withdraw $60,000 each year to live on.Assume that the $60,000 is withdrawn on the last day of the year.Find a recursive formula for 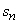 , the amount of money left in the account at the end of n years, and use it to determine how many years the money will last (how many years until there is less than $60,000 in the account).
, the amount of money left in the account at the end of n years, and use it to determine how many years the money will last (how many years until there is less than $60,000 in the account).
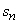 , the amount of money left in the account at the end of n years, and use it to determine how many years the money will last (how many years until there is less than $60,000 in the account).
, the amount of money left in the account at the end of n years, and use it to determine how many years the money will last (how many years until there is less than $60,000 in the account).
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
15
A radioactive isotope is released into the air as an industrial by-product.This isotope is not very stable due to radioactive decay.Two-thirds of the original radioactive material loses its radioactivity after each month.If 12 grams of this isotope are released into the atmosphere at the end of the first and every subsequent month, identify the closed form sum that gives the amount of the isotope in the atmosphere at the end of the nth month.
A)
B)
C)
A)
B)
C)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
16
Compute the first 8 terms of the sequence 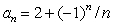 on plot them on a number line.To what number does it appear the sequence converges, if any?
on plot them on a number line.To what number does it appear the sequence converges, if any?
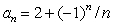 on plot them on a number line.To what number does it appear the sequence converges, if any?
on plot them on a number line.To what number does it appear the sequence converges, if any?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
17
Stock prices for Abercrombie and Fitch fell steadily by an average of $0.94 per day from a high of $83.67 per share on December 24, 2007 to $70.05 on January 15, 2008.Let 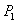 be the price of a share of stock on December 24, 2007 and
be the price of a share of stock on December 24, 2007 and 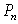 be the price of a share on the
be the price of a share on the 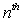 day after December 24.Write a formula for
day after December 24.Write a formula for 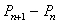 and then write a sentence to interpret the meaning of your formula.
and then write a sentence to interpret the meaning of your formula.
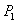 be the price of a share of stock on December 24, 2007 and
be the price of a share of stock on December 24, 2007 and 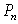 be the price of a share on the
be the price of a share on the 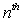 day after December 24.Write a formula for
day after December 24.Write a formula for 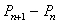 and then write a sentence to interpret the meaning of your formula.
and then write a sentence to interpret the meaning of your formula.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
18
Consider the finite sequence given in the graph below.Find . 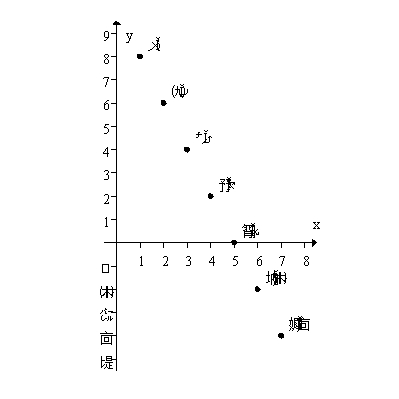
A)60
B)15
C)75
D)56
E)None of the above

A)60
B)15
C)75
D)56
E)None of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
19
Which one of the following sequences diverges to positive infinity as n ?
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find a recursive formula for , n 1, for the sequence 1, 6, 41, 286, 2001, ...
A) with
B) with
C) with
D) with
A) with
B) with
C) with
D) with

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
21
Does the infinite series 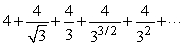 converge or diverge?
converge or diverge?
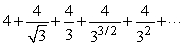 converge or diverge?
converge or diverge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
22
Find the sum 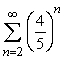 .Round to 2 decimal places.
.Round to 2 decimal places.
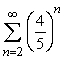 .Round to 2 decimal places.
.Round to 2 decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
23
Use the integral test to decide whether the series converges or diverges.
A)It converges
B)It diverges
A)It converges
B)It diverges

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
24
Suppose the government spends $3.5 million on highways.Some of this money is earned by the highway workers who in turn spend $1,750,000 on food, travel, and entertainment.This causes $875,000 to be spent by the people who work in the food, travel, and entertainment industries.This $875,000 causes another $437,500 to be spent; the $437,500 causes another $218,750 to be spent, and so on.(Notice that each expenditure is half the previous one.)Assuming that this process continues forever, how many million dollars in total spending is generated by the original $3.5 million expenditure (including the original $3.5 million)?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
25
Is 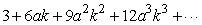 a geometric series?
a geometric series?
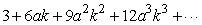 a geometric series?
a geometric series?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
26
Jamie was born in May.In August, her grandparents started a "Go to College in France" fund with $2200, earning a fixed annual interest rate of 7%.They added an additional $2200 each year in August until the last deposit in the year Jamie turned 18.Jamie estimated that she needed $90,000 to go start college in France.How much did she have in her "Go to College in France" fund? Did she have enough?
A) , no
B) , no
C)$91533.97, yes
D)$87533.83, no
E) , no
A) , no
B) , no
C)$91533.97, yes
D)$87533.83, no
E) , no

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
27
Does 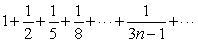 converge or diverge?
converge or diverge?
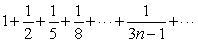 converge or diverge?
converge or diverge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
28
Which of the following series are geometric? (1)
(2)
(3)
A)(1)and (2)
B)(1)and (3)
C)(2)and (3)
D)(1)only
E)(2)only
(2)
(3)

A)(1)and (2)
B)(1)and (3)
C)(2)and (3)
D)(1)only
E)(2)only

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
29
Does the series 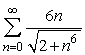 converge or diverge?
converge or diverge?
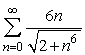 converge or diverge?
converge or diverge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the 6th partial sum of the series (to two decimal places).
A)26.12
B)
C)83.28
D)248.66
A)26.12
B)
C)83.28
D)248.66

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
31
A ball is dropped from a height of 18 feet and bounces.Each bounce is 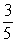 of the height of the bounce before.Find the total vertical feet the ball has traveled when it hits the floor for the 4th time.Round to 1 decimal place.
of the height of the bounce before.Find the total vertical feet the ball has traveled when it hits the floor for the 4th time.Round to 1 decimal place.
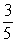 of the height of the bounce before.Find the total vertical feet the ball has traveled when it hits the floor for the 4th time.Round to 1 decimal place.
of the height of the bounce before.Find the total vertical feet the ball has traveled when it hits the floor for the 4th time.Round to 1 decimal place.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
32
A tennis ball is dropped from a height of 15 feet and bounces.Each bounce is the height of the bounce before.A superball has a bounce the height of the bounce before, and is dropped from a height of 5 feet.Which ball bounces a greater total vertical distance?
A)The tennis ball
B)The superball
A)The tennis ball
B)The superball

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
33
Find the sum of the first 6 terms of the series 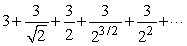 .Round to 2 decimal places.
.Round to 2 decimal places.
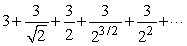 .Round to 2 decimal places.
.Round to 2 decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
34
Find the sum of the series 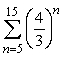 to 2 decimal places.
to 2 decimal places.
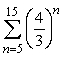 to 2 decimal places.
to 2 decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
35
Does the series 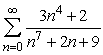 converge or diverge?
converge or diverge?
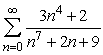 converge or diverge?
converge or diverge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
36
A ball is dropped from a height of 11 feet and bounces.Each bounce is of the height of the bounce before.Find an expression for the height to which the ball rises after it hits the floor for the nth time.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
37
Use the integral test, if applicable, to determine whether the series converges or diverges.
A)It converges.
B)It diverges.
C)The integral test does not apply.
A)It converges.
B)It diverges.
C)The integral test does not apply.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
38
Use the integral test to decide whether the series 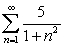 converges or diverges.
converges or diverges.
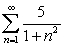 converges or diverges.
converges or diverges.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
39
Does the series 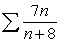 converge or diverge.Explain.
converge or diverge.Explain.
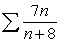 converge or diverge.Explain.
converge or diverge.Explain.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
40
Consider the series: 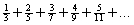
(a)Find a formula for the general term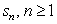 .
.
(b)Find the partial sums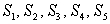 .
.
(c)Use your result from part (b)to predict the limit of the partial sums,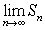 .Does this indicate that the series converges or diverges?
.Does this indicate that the series converges or diverges?
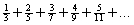
(a)Find a formula for the general term
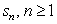 .
.(b)Find the partial sums
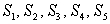 .
.(c)Use your result from part (b)to predict the limit of the partial sums,
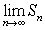 .Does this indicate that the series converges or diverges?
.Does this indicate that the series converges or diverges?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
41
If converges then converges (k 0).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
42
Determine whether the following series converge or diverge:
a)
b)
A)(a)converges and (b)diverges
B)(a)diverges and (b)converges
C)both series diverge
D)both series converge
a)
b)
A)(a)converges and (b)diverges
B)(a)diverges and (b)converges
C)both series diverge
D)both series converge

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the interval of convergence for .
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
44
If a power series converges at x = c then it also converges at x = -c.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
45
Use the alternating series test to decide if converges.
A)It converges.
B)It diverges.
A)It converges.
B)It diverges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
46
If a power series converges at x = 6 and x = 7 then it converges at x = -6.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
47
Use the comparison test to determine whether converges.
A)It converges.
B)It diverges.
A)It converges.
B)It diverges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
48
The harmonic series diverges.We can form a new series from the difference between consecutive terms of the harmonic series obtaining . This series also diverges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
49
Use the limit comparison test to determine whether converges.
A)The series diverges.
B)The series converges.
A)The series diverges.
B)The series converges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
50
What does the ratio test tell us about the series ?
A)The series converges.
B)The series diverges.
C)The ratio test doesn't tell us anything about the convergence of the series.
A)The series converges.
B)The series diverges.
C)The ratio test doesn't tell us anything about the convergence of the series.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
51
Estimate the error in approximating the sum of the alternating series by the sum of the first 11 terms.
A)0.000024
B)0.00024
C)0.0024
D)0.024
A)0.000024
B)0.00024
C)0.0024
D)0.024

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
52
If the series 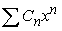 has a radius of convergence of 4 and
has a radius of convergence of 4 and 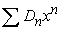 has a radius of convergence of 6, what is the radius of convergence of
has a radius of convergence of 6, what is the radius of convergence of 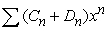 ?
?
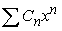 has a radius of convergence of 4 and
has a radius of convergence of 4 and 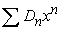 has a radius of convergence of 6, what is the radius of convergence of
has a radius of convergence of 6, what is the radius of convergence of 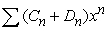 ?
?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
53
If a series of constants 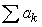 diverges, then must
diverges, then must 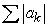 diverge?
diverge?
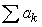 diverges, then must
diverges, then must 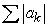 diverge?
diverge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
54
Leonard Euler found the following series to be noteworthy because it is part of a process that can be used to approximate 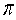 :
: 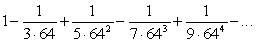
(a)Re-write this series in summation notation.
(b)Use an appropriate test to show that the series converges.
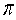 :
: 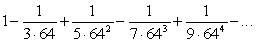
(a)Re-write this series in summation notation.
(b)Use an appropriate test to show that the series converges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
55
If is the sum of a series of numbers and , then the series converges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find an expression for the general term of the series
A) for .
B) for .
C) for .
D) for .
A) for .
B) for .
C) for .
D) for .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
57
What does the ratio test tell us about the series ?
A)The series converges.
B)The series diverges.
C)The ratio test doesn't tell us anything about the convergence of the series.
A)The series converges.
B)The series diverges.
C)The ratio test doesn't tell us anything about the convergence of the series.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
58
Use the ratio test to find the radius of convergence of 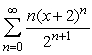 .
.
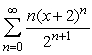 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
59
If is not zero, then does not converge.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
60
What does the ratio test tell us about the series ?
A)The series diverges.
B)The series converges.
C)The ratio test doesn't tell us anything about the convergence of the series.
A)The series diverges.
B)The series converges.
C)The ratio test doesn't tell us anything about the convergence of the series.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
61
If the power series converges for , then it converges for .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
62
Find the radius of convergence of 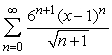 .
.
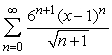 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
63
Does 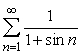 converge?
converge?
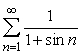 converge?
converge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
64
If is convergent, then is also convergent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
65
Find the radius of convergence of 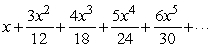
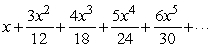

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
66
The ratio test can be used to determine whether converges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
67
Find the interval of convergence of the series 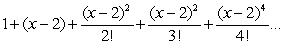
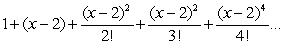

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
68
Does 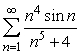 converge?
converge?
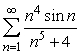 converge?
converge?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
69
For what values of p does the series converge, if any?
A)
B)
C)-1 < p < 1
D)
E)The series diverges for all values of p.
A)
B)
C)-1 < p < 1
D)
E)The series diverges for all values of p.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck
70
If (for all n)and converges, then converges.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 70 في هذه المجموعة.
فتح الحزمة
k this deck








