Deck 6: Linear Regression With Multiple Regressors
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/54
العب
ملء الشاشة (f)
Deck 6: Linear Regression With Multiple Regressors
1
If you had a two regressor regression model, then omitting one variable which is relevant
A)will have no effect on the coefficient of the included variable if the correlation between the excluded and the included variable is negative.
B)will always bias the coefficient of the included variable upwards.
C)can result in a negative value for the coefficient of the included variable, even though the coefficient will have a significant positive effect on Y if the omitted
Variable were included.
D)makes the sum of the product between the included variable and the residuals different from 0.
A)will have no effect on the coefficient of the included variable if the correlation between the excluded and the included variable is negative.
B)will always bias the coefficient of the included variable upwards.
C)can result in a negative value for the coefficient of the included variable, even though the coefficient will have a significant positive effect on Y if the omitted
Variable were included.
D)makes the sum of the product between the included variable and the residuals different from 0.
C
2
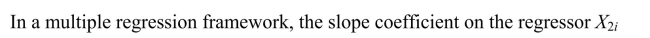

B
3
When you have an omitted variable problem, the assumption that is violated. This implies that
A) the sum of the residuals is no longer zero.
B) there is another estimator called weighted least squares, which is BLUE.
C) the sum of the residuals times any of the explanatory variables is no longer zero.
D) the OLS estimator is no longer consistent.
A) the sum of the residuals is no longer zero.
B) there is another estimator called weighted least squares, which is BLUE.
C) the sum of the residuals times any of the explanatory variables is no longer zero.
D) the OLS estimator is no longer consistent.
the OLS estimator is no longer consistent.
4
The OLS residuals in the multiple regression model
A)cannot be calculated because there is more than one explanatory variable.
B)can be calculated by subtracting the fitted values from the actual values.
C)are zero because the predicted values are another name for forecasted values.
D)are typically the same as the population regression function errors.
A)cannot be calculated because there is more than one explanatory variable.
B)can be calculated by subtracting the fitted values from the actual values.
C)are zero because the predicted values are another name for forecasted values.
D)are typically the same as the population regression function errors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
5
(Requires Calculus) In the multiple regression model you estimate the effect on of a unit change in one of the while holding all other regressors constant. This
A) makes little sense, because in the real world all other variables change.
B) corresponds to the economic principle of mutatis mutandis.
C) leaves the formula for the coefficient in the single explanatory variable case unaffected.
D) corresponds to taking a partial derivative in mathematics.
A) makes little sense, because in the real world all other variables change.
B) corresponds to the economic principle of mutatis mutandis.
C) leaves the formula for the coefficient in the single explanatory variable case unaffected.
D) corresponds to taking a partial derivative in mathematics.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
6
Under the least squares assumptions for the multiple regression problem (zero conditional mean for the error term, all being i.i.d., all having finite fourth moments, no perfect multicollinearity), the OLS estimators for the slopes and intercept
A) have an exact normal distribution for n>25 .
B) are BLUE.
C) have a normal distribution in small samples as long as the errors are homoskedastic.
D) are unbiased and consistent.
A) have an exact normal distribution for n>25 .
B) are BLUE.
C) have a normal distribution in small samples as long as the errors are homoskedastic.
D) are unbiased and consistent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
7
One of the least squares assumptions in the multiple regression model is that you have random variables which are "i.i.d." This stands for
A)initially indeterminate differences.
B)irregularly integrated dichotomies.
C)identically initiated deltas (as in changes).
D)independently and identically distributed.
A)initially indeterminate differences.
B)irregularly integrated dichotomies.
C)identically initiated deltas (as in changes).
D)independently and identically distributed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
8
You have to worry about perfect multicollinearity in the multiple regression model because
A)many economic variables are perfectly correlated.
B)the OLS estimator is no longer BLUE.
C)the OLS estimator cannot be computed in this situation.
D)in real life, economic variables change together all the time.
A)many economic variables are perfectly correlated.
B)the OLS estimator is no longer BLUE.
C)the OLS estimator cannot be computed in this situation.
D)in real life, economic variables change together all the time.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
9
Omitted variable bias 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
10
In the multiple regression model, the least squares estimator is derived by
A)minimizing the sum of squared prediction mistakes.
B)setting the sum of squared errors equal to zero.
C)minimizing the absolute difference of the residuals.
D)forcing the smallest distance between the actual and fitted values.
A)minimizing the sum of squared prediction mistakes.
B)setting the sum of squared errors equal to zero.
C)minimizing the absolute difference of the residuals.
D)forcing the smallest distance between the actual and fitted values.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
11
Under imperfect multicollinearity
A)the OLS estimator cannot be computed.
B)two or more of the regressors are highly correlated.
C)the OLS estimator is biased even in samples of n > 100.
D)the error terms are highly, but not perfectly, correlated.
A)the OLS estimator cannot be computed.
B)two or more of the regressors are highly correlated.
C)the OLS estimator is biased even in samples of n > 100.
D)the error terms are highly, but not perfectly, correlated.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
12
The sample regression line estimated by OLS
A)has an intercept that is equal to zero.
B)is the same as the population regression line.
C)cannot have negative and positive slopes.
D)is the line that minimizes the sum of squared prediction mistakes.
A)has an intercept that is equal to zero.
B)is the same as the population regression line.
C)cannot have negative and positive slopes.
D)is the line that minimizes the sum of squared prediction mistakes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
13
In the multiple regression model, the adjusted
A) cannot be negative.
B) will never be greater than the regression
C) equals the square of the correlation coefficient r .
D) cannot decrease when an additional explanatory variable is added.
A) cannot be negative.
B) will never be greater than the regression
C) equals the square of the correlation coefficient r .
D) cannot decrease when an additional explanatory variable is added.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
14
The intercept in the multiple regression model
A)should be excluded if one explanatory variable has negative values.
B)determines the height of the regression line.
C)should be excluded because the population regression function does not go through the origin.
D)is statistically significant if it is larger than 1.96.
A)should be excluded if one explanatory variable has negative values.
B)determines the height of the regression line.
C)should be excluded because the population regression function does not go through the origin.
D)is statistically significant if it is larger than 1.96.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
15
The main advantage of using multiple regression analysis over differences in means testing is that the regression technique
A)allows you to calculate p-values for the significance of your results.
B)provides you with a measure of your goodness of fit.
C)gives you quantitative estimates of a unit change in X.
D)assumes that the error terms are generated from a normal distribution.
A)allows you to calculate p-values for the significance of your results.
B)provides you with a measure of your goodness of fit.
C)gives you quantitative estimates of a unit change in X.
D)assumes that the error terms are generated from a normal distribution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
16
In a two regressor regression model, if you exclude one of the relevant variables then
A)it is no longer reasonable to assume that the errors are homoskedastic.
B)OLS is no longer unbiased, but still consistent.
C)you are no longer controlling for the influence of the other variable.
D)the OLS estimator no longer exists.
A)it is no longer reasonable to assume that the errors are homoskedastic.
B)OLS is no longer unbiased, but still consistent.
C)you are no longer controlling for the influence of the other variable.
D)the OLS estimator no longer exists.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
17
The following OLS assumption is most likely violated by omitted variables bias: 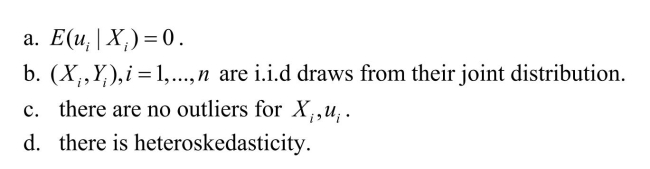
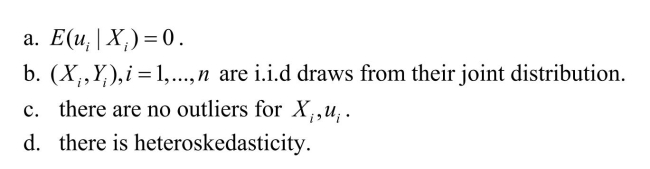

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
18
Imagine you regressed earnings of individuals on a constant, a binary variable ("Male") which takes on the value 1 for males and is 0 otherwise, and another binary variable ("Female") which takes on the value 1 for females and is 0 otherwise. Because females typically earn less than males, you would expect
A) the coefficient for Male to have a positive sign, and for Female a negative sign.
B) both coefficients to be the same distance from the constant, one above and the other below.
C) none of the OLS estimators to exist because there is perfect multicollinearity.
D) this to yield a difference in means statistic.
A) the coefficient for Male to have a positive sign, and for Female a negative sign.
B) both coefficients to be the same distance from the constant, one above and the other below.
C) none of the OLS estimators to exist because there is perfect multicollinearity.
D) this to yield a difference in means statistic.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
19
When there are omitted variables in the regression, which are determinants of the dependent variable, then
A)you cannot measure the effect of the omitted variable, but the estimator of your included variable(s)is (are)unaffected.
B)this has no effect on the estimator of your included variable because the other variable is not included.
C)this will always bias the OLS estimator of the included variable.
D)the OLS estimator is biased if the omitted variable is correlated with the included variable.
A)you cannot measure the effect of the omitted variable, but the estimator of your included variable(s)is (are)unaffected.
B)this has no effect on the estimator of your included variable because the other variable is not included.
C)this will always bias the OLS estimator of the included variable.
D)the OLS estimator is biased if the omitted variable is correlated with the included variable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
20
The population multiple regression model when there are two regressors, can be written as follows, with the exception of:
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
21
Attendance at sports events depends on various factors.Teams typically do not change
ticket prices from game to game to attract more spectators to less attractive games.
However, there are other marketing tools used, such as fireworks, free hats, etc., for this
purpose.You work as a consultant for a sports team, the Los Angeles Dodgers, to help
them forecast attendance, so that they can potentially devise strategies for price
discrimination.After collecting data over two years for every one of the 162 home games
of the 2000 and 2001 season, you run the following regression: where Attend is announced stadium attendance, Temperat it the average temperature on
where Attend is announced stadium attendance, Temperat it the average temperature on
game day, DodgNetWin are the net wins of the Dodgers before the game (wins-losses),
OppNetWin is the opposing team's net wins at the end of the previous season, and
DFSaSu, Drain, D150m, Ddiv, and D2001 are binary variables, taking a value of 1 if the
game was played on a weekend, it rained during that day, the opposing team was within a
150 mile radius, the opposing team plays in the same division as the Dodgers, and the
game was played during 2001, respectively.
(a)Interpret the regression results.Do the coefficients have the expected signs?
ticket prices from game to game to attract more spectators to less attractive games.
However, there are other marketing tools used, such as fireworks, free hats, etc., for this
purpose.You work as a consultant for a sports team, the Los Angeles Dodgers, to help
them forecast attendance, so that they can potentially devise strategies for price
discrimination.After collecting data over two years for every one of the 162 home games
of the 2000 and 2001 season, you run the following regression:
 where Attend is announced stadium attendance, Temperat it the average temperature on
where Attend is announced stadium attendance, Temperat it the average temperature ongame day, DodgNetWin are the net wins of the Dodgers before the game (wins-losses),
OppNetWin is the opposing team's net wins at the end of the previous season, and
DFSaSu, Drain, D150m, Ddiv, and D2001 are binary variables, taking a value of 1 if the
game was played on a weekend, it rained during that day, the opposing team was within a
150 mile radius, the opposing team plays in the same division as the Dodgers, and the
game was played during 2001, respectively.
(a)Interpret the regression results.Do the coefficients have the expected signs?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
22
In the multiple regression model with two regressors, the formula for the slope of the first
explanatory variable is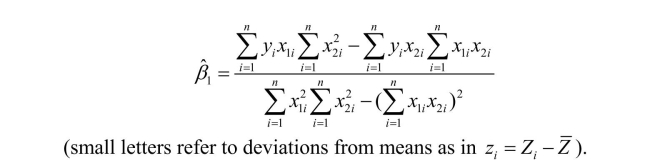 An alternative way to derive the OLS estimator is given through the following three step
An alternative way to derive the OLS estimator is given through the following three step
procedure. Prove that the slope of the regression in Step 3 is identical to the above formula.
Prove that the slope of the regression in Step 3 is identical to the above formula.
explanatory variable is
 An alternative way to derive the OLS estimator is given through the following three step
An alternative way to derive the OLS estimator is given through the following three stepprocedure.
 Prove that the slope of the regression in Step 3 is identical to the above formula.
Prove that the slope of the regression in Step 3 is identical to the above formula.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
23
You have collected data for 104 countries to address the difficult questions of the
determinants for differences in the standard of living among the countries of the world.
You recall from your macroeconomics lectures that the neoclassical growth model
suggests that output per worker (per capita income)levels are determined by, among
others, the saving rate and population growth rate.To test the predictions of this growth
model, you run the following regression: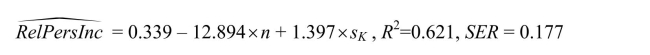 where RelPersInc is GDP per worker relative to the United States, n is the average
where RelPersInc is GDP per worker relative to the United States, n is the average
population growth rate, 1980-1990, and sK is the average investment share of GDP from
1960 to1990 (remember investment equals saving).
(a)Interpret the results.Do the signs correspond to what you expected them to be? Explain.
determinants for differences in the standard of living among the countries of the world.
You recall from your macroeconomics lectures that the neoclassical growth model
suggests that output per worker (per capita income)levels are determined by, among
others, the saving rate and population growth rate.To test the predictions of this growth
model, you run the following regression:
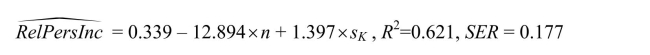 where RelPersInc is GDP per worker relative to the United States, n is the average
where RelPersInc is GDP per worker relative to the United States, n is the averagepopulation growth rate, 1980-1990, and sK is the average investment share of GDP from
1960 to1990 (remember investment equals saving).
(a)Interpret the results.Do the signs correspond to what you expected them to be? Explain.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
24
In multiple regression, the increases whenever a regressor is
A) added unless the coefficient on the added regressor is exactly zero.
B) added.
C) added unless there is heterosckedasticity.
D) greater than 1.96 in absolute value.
A) added unless the coefficient on the added regressor is exactly zero.
B) added.
C) added unless there is heterosckedasticity.
D) greater than 1.96 in absolute value.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
25
Females, on average, are shorter and weigh less than males.One of your friends, who is a
pre-med student, tells you that in addition, females will weigh less for a given height.To
test this hypothesis, you collect height and weight of 29 female and 81 male students at
your university.A regression of the weight on a constant, height, and a binary variable,
which takes a value of one for females and is zero otherwise, yields the following result: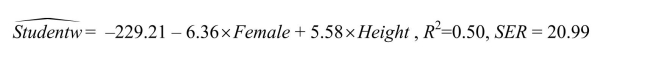 where Studentw is weight measured in pounds and Height is measured in inches.
where Studentw is weight measured in pounds and Height is measured in inches.
(a)Interpret the results.Does it make sense to have a negative intercept?
pre-med student, tells you that in addition, females will weigh less for a given height.To
test this hypothesis, you collect height and weight of 29 female and 81 male students at
your university.A regression of the weight on a constant, height, and a binary variable,
which takes a value of one for females and is zero otherwise, yields the following result:
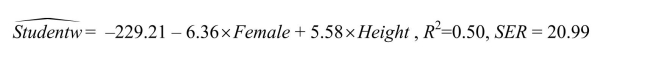 where Studentw is weight measured in pounds and Height is measured in inches.
where Studentw is weight measured in pounds and Height is measured in inches.(a)Interpret the results.Does it make sense to have a negative intercept?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
26
In the multiple regression model, the SER is given by 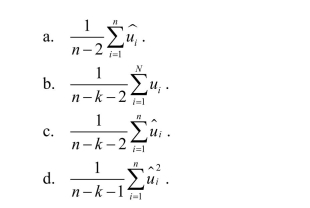
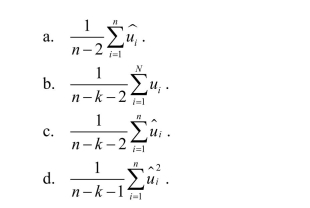

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
27
The administration of your university/college is thinking about implementing a policy of
coed floors only in dormitories.Currently there are only single gender floors.One reason
behind such a policy might be to generate an atmosphere of better "understanding"
between the sexes.The Dean of Students (DoS)has decided to investigate if such a
behavior results in more "togetherness" by attempting to find the determinants of the
gender composition at the dinner table in your main dining hall, and in that of a
neighboring university, which only allows for coed floors in their dorms.The survey
includes 176 students, 63 from your university/college, and 113 from a neighboring
institution.
(a)The Dean's first problem is how to define gender composition.To begin with, the survey
excludes single persons' tables, since the study is to focus on group behavior.The Dean
also eliminates sports teams from the analysis, since a large number of single-gender
students will sit at the same table.Finally, the Dean decides to only analyze tables with
three or more students, since she worries about "couples" distorting the results.The Dean
finally settles for the following specification of the dependent variable:
GenderComp=|(50%-% of Male Students at Table)|
coed floors only in dormitories.Currently there are only single gender floors.One reason
behind such a policy might be to generate an atmosphere of better "understanding"
between the sexes.The Dean of Students (DoS)has decided to investigate if such a
behavior results in more "togetherness" by attempting to find the determinants of the
gender composition at the dinner table in your main dining hall, and in that of a
neighboring university, which only allows for coed floors in their dorms.The survey
includes 176 students, 63 from your university/college, and 113 from a neighboring
institution.
(a)The Dean's first problem is how to define gender composition.To begin with, the survey
excludes single persons' tables, since the study is to focus on group behavior.The Dean
also eliminates sports teams from the analysis, since a large number of single-gender
students will sit at the same table.Finally, the Dean decides to only analyze tables with
three or more students, since she worries about "couples" distorting the results.The Dean
finally settles for the following specification of the dependent variable:
GenderComp=|(50%-% of Male Students at Table)|


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
28
Consider the following multiple regression models (a)to (d)below.DFemme = 1 if the individual is a female, and is zero otherwise; DMale is a binary variable which takes on
The value one if the individual is male, and is zero otherwise; DMarried is a binary
Variable which is unity for married individuals and is zero otherwise, and DSingle is (1-
DMarried).Regressing weekly earnings (Earn)on a set of explanatory variables, you will
Experience perfect multicollinearity in the following cases unless: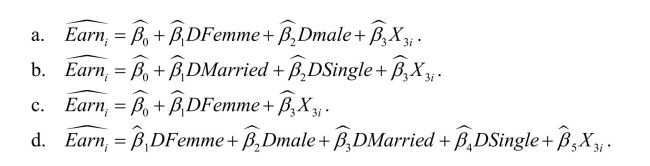
The value one if the individual is male, and is zero otherwise; DMarried is a binary
Variable which is unity for married individuals and is zero otherwise, and DSingle is (1-
DMarried).Regressing weekly earnings (Earn)on a set of explanatory variables, you will
Experience perfect multicollinearity in the following cases unless:
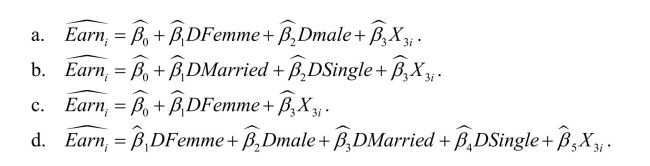

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
29
The Solow growth model suggests that countries with identical saving rates and
population growth rates should converge to the same per capita income level.This result
has been extended to include investment in human capital (education)as well as
investment in physical capital.This hypothesis is referred to as the "conditional
convergence hypothesis," since the convergence is dependent on countries obtaining the
same values in the driving variables.To test the hypothesis, you collect data from the
Penn World Tables on the average annual growth rate of GDP per worker (g6090)for the
1960-1990 sample period, and regress it on the (i)initial starting level of GDP per worker
relative to the United States in 1960 (RelProd60), (ii)average population growth rate of
the country (n), (iii)average investment share of GDP from 1960 to1990 (sK - remember
investment equals savings), and (iv)educational attainment in years for 1985 (Educ).The
results for close to 100 countries is as follows: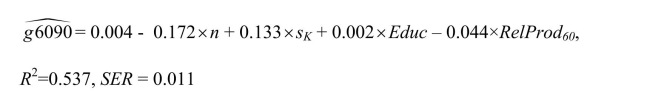 (a)Interpret the results.Do the coefficients have the expected signs? Why does a negative
(a)Interpret the results.Do the coefficients have the expected signs? Why does a negative
coefficient on the initial level of per capita income indicate conditional convergence
("beta-convergence")?
population growth rates should converge to the same per capita income level.This result
has been extended to include investment in human capital (education)as well as
investment in physical capital.This hypothesis is referred to as the "conditional
convergence hypothesis," since the convergence is dependent on countries obtaining the
same values in the driving variables.To test the hypothesis, you collect data from the
Penn World Tables on the average annual growth rate of GDP per worker (g6090)for the
1960-1990 sample period, and regress it on the (i)initial starting level of GDP per worker
relative to the United States in 1960 (RelProd60), (ii)average population growth rate of
the country (n), (iii)average investment share of GDP from 1960 to1990 (sK - remember
investment equals savings), and (iv)educational attainment in years for 1985 (Educ).The
results for close to 100 countries is as follows:
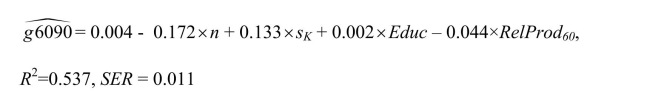 (a)Interpret the results.Do the coefficients have the expected signs? Why does a negative
(a)Interpret the results.Do the coefficients have the expected signs? Why does a negativecoefficient on the initial level of per capita income indicate conditional convergence
("beta-convergence")?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
30
In the multiple regression model
the OLS estimators are obtained by minimizing the sum of
A) squared mistakes in
B) squared mistakes in
C) absolute mistakes in
D) squared mistakes in
the OLS estimators are obtained by minimizing the sum of
A) squared mistakes in
B) squared mistakes in
C) absolute mistakes in
D) squared mistakes in

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
31
 Can you give an intuitive explanation to this procedure?
Can you give an intuitive explanation to this procedure?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
32
You have obtained data on test scores and student-teacher ratios in region A and region B
of your state.Region B, on average, has lower student-teacher ratios than region A.You
decide to run the following regression where X1 is the class size in region A, X2 is the difference in class size between region A
where X1 is the class size in region A, X2 is the difference in class size between region A
and B, and X3 is the class size in region B.Your regression package shows a message
indicating that it cannot estimate the above equation.What is the problem here and how
can it be fixed?
of your state.Region B, on average, has lower student-teacher ratios than region A.You
decide to run the following regression
 where X1 is the class size in region A, X2 is the difference in class size between region A
where X1 is the class size in region A, X2 is the difference in class size between region Aand B, and X3 is the class size in region B.Your regression package shows a message
indicating that it cannot estimate the above equation.What is the problem here and how
can it be fixed?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
33
You try to establish that there is a positive relationship between the use of a fertilizer and
the growth of a certain plant.Set up the design of an experiment to establish the
relationship, paying particular attention to relevant control variables.Discuss in this
context the effect of omitted variable bias.
the growth of a certain plant.Set up the design of an experiment to establish the
relationship, paying particular attention to relevant control variables.Discuss in this
context the effect of omitted variable bias.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
34
Your econometrics textbook stated that there will be omitted variable bias in the OLS
estimator unless the included regressor, X, is uncorrelated with the omitted variable or the
omitted variable is not a determinant of the dependent variable, Y.Give an intuitive
explanation for these two conditions.
estimator unless the included regressor, X, is uncorrelated with the omitted variable or the
omitted variable is not a determinant of the dependent variable, Y.Give an intuitive
explanation for these two conditions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
35
The cost of attending your college has once again gone up.Although you have been told
that education is investment in human capital, which carries a return of roughly 10% a
year, you (and your parents)are not pleased.One of the administrators at your
university/college does not make the situation better by telling you that you pay more
because the reputation of your institution is better than that of others.To investigate this
hypothesis, you collect data randomly for 100 national universities and liberal arts
colleges from the 2000-2001 U.S.News and World Report annual rankings.Next you
perform the following regression where Cost is Tuition, Fees, Room and Board in dollars, Reputation is the index used in
where Cost is Tuition, Fees, Room and Board in dollars, Reputation is the index used in
U.S.News and World Report (based on a survey of university presidents and chief
academic officers), which ranges from 1 ("marginal")to 5 ("distinguished"), Size is the
number of undergraduate students, and Dpriv, Dlibart, and Dreligion are binary variables
indicating whether the institution is private, a liberal arts college, and has a religious
affiliation.
(a)Interpret the results.Do the coefficients have the expected sign?
that education is investment in human capital, which carries a return of roughly 10% a
year, you (and your parents)are not pleased.One of the administrators at your
university/college does not make the situation better by telling you that you pay more
because the reputation of your institution is better than that of others.To investigate this
hypothesis, you collect data randomly for 100 national universities and liberal arts
colleges from the 2000-2001 U.S.News and World Report annual rankings.Next you
perform the following regression
 where Cost is Tuition, Fees, Room and Board in dollars, Reputation is the index used in
where Cost is Tuition, Fees, Room and Board in dollars, Reputation is the index used inU.S.News and World Report (based on a survey of university presidents and chief
academic officers), which ranges from 1 ("marginal")to 5 ("distinguished"), Size is the
number of undergraduate students, and Dpriv, Dlibart, and Dreligion are binary variables
indicating whether the institution is private, a liberal arts college, and has a religious
affiliation.
(a)Interpret the results.Do the coefficients have the expected sign?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
36
In the case of perfect multicollinearity, OLS is unable to calculate the coefficients for the
explanatory variables, because it is impossible to change one variable while holding all
other variables constant.To see why this is the case, consider the coefficient for the first
explanatory variable in the case of a multiple regression model with two explanatory
variables: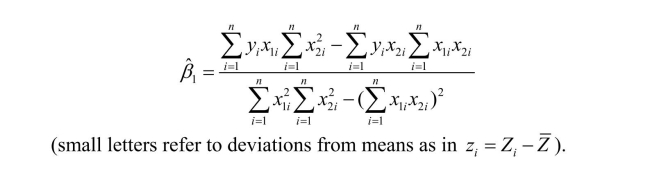

explanatory variables, because it is impossible to change one variable while holding all
other variables constant.To see why this is the case, consider the coefficient for the first
explanatory variable in the case of a multiple regression model with two explanatory
variables:
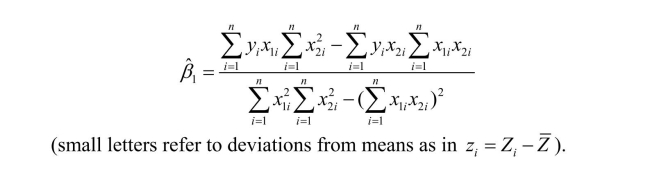


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
37
You have collected data from Major League Baseball (MLB)to find the determinants of
winning.You have a general idea that both good pitching and strong hitting are needed to do
well.However, you do not know how much each of these contributes separately.To
investigate this problem, you collect data for all MLB during 1999 season.Your strategy is to
first regress the winning percentage on pitching quality ("Team ERA"), second to regress the
same variable on some measure of hitting ("OPS - On-base Plus Slugging percentage"), and
third to regress the winning percentage on both.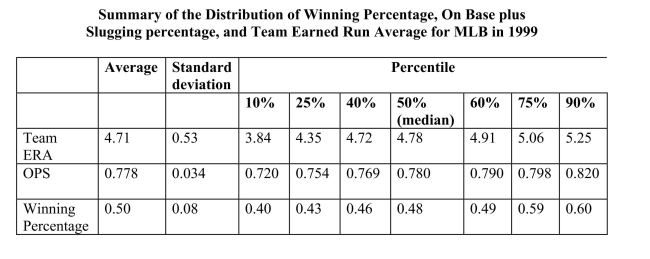
 (a)Interpret the multiple regression.What is the effect of a one point increase in team ERA?
(a)Interpret the multiple regression.What is the effect of a one point increase in team ERA?
Given that the Atlanta Braves had the most wins that year, wining 103 games out of 162,
do you find this effect important? Next analyze the importance and statistical significance
for the OPS coefficient.(The Minnesota Twins had the minimum OPS of 0.712, while
the Texas Rangers had the maximum with 0.840.)Since the intercept is negative, and
since winning percentages must lie between zero and one, should you rerun the
regression through the origin?
winning.You have a general idea that both good pitching and strong hitting are needed to do
well.However, you do not know how much each of these contributes separately.To
investigate this problem, you collect data for all MLB during 1999 season.Your strategy is to
first regress the winning percentage on pitching quality ("Team ERA"), second to regress the
same variable on some measure of hitting ("OPS - On-base Plus Slugging percentage"), and
third to regress the winning percentage on both.

 (a)Interpret the multiple regression.What is the effect of a one point increase in team ERA?
(a)Interpret the multiple regression.What is the effect of a one point increase in team ERA?Given that the Atlanta Braves had the most wins that year, wining 103 games out of 162,
do you find this effect important? Next analyze the importance and statistical significance
for the OPS coefficient.(The Minnesota Twins had the minimum OPS of 0.712, while
the Texas Rangers had the maximum with 0.840.)Since the intercept is negative, and
since winning percentages must lie between zero and one, should you rerun the
regression through the origin?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
38
In the multiple regression model with two explanatory variables 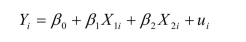

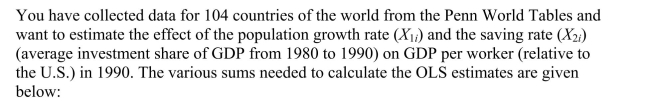
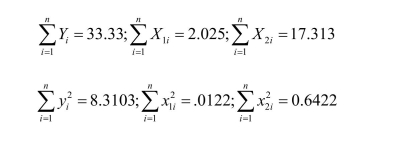
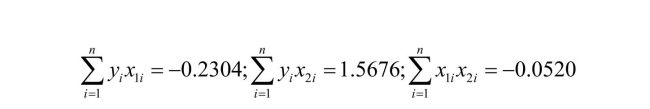 (a)What are your expected signs for the regression coefficient? Calculate the coefficients
(a)What are your expected signs for the regression coefficient? Calculate the coefficients
and see if their signs correspond to your intuition.
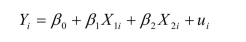

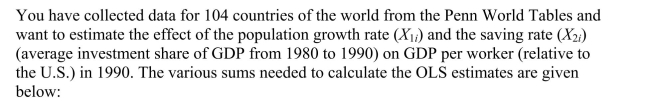
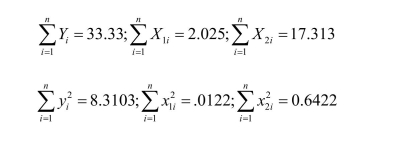
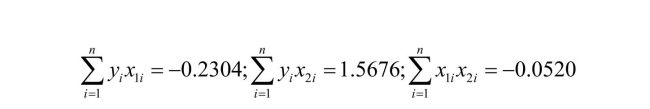 (a)What are your expected signs for the regression coefficient? Calculate the coefficients
(a)What are your expected signs for the regression coefficient? Calculate the coefficientsand see if their signs correspond to your intuition.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
39
A subsample from the Current Population Survey is taken, on weekly earnings of
individuals, their age, and their gender.You have read in the news that women make 70
cents to the $1 that men earn.To test this hypothesis, you first regress earnings on a
constant and a binary variable, which takes on a value of 1 for females and is 0 otherwise.
The results were: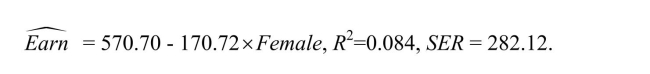 (a)There are 850 females in your sample and 894 males.What are the mean earnings of
(a)There are 850 females in your sample and 894 males.What are the mean earnings of
males and females in this sample? What is the percentage of average female income to
male income?
individuals, their age, and their gender.You have read in the news that women make 70
cents to the $1 that men earn.To test this hypothesis, you first regress earnings on a
constant and a binary variable, which takes on a value of 1 for females and is 0 otherwise.
The results were:
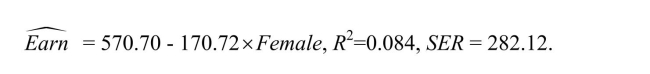 (a)There are 850 females in your sample and 894 males.What are the mean earnings of
(a)There are 850 females in your sample and 894 males.What are the mean earnings ofmales and females in this sample? What is the percentage of average female income to
male income?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
40
In the process of collecting weight and height data from 29 female and 81 male students
at your university, you also asked the students for the number of siblings they have.
Although it was not quite clear to you initially what you would use that variable for, you
construct a new theory that suggests that children who have more siblings come from
poorer families and will have to share the food on the table.Although a friend tells you
that this theory does not pass the "straight-face" test, you decide to hypothesize that peers
with many siblings will weigh less, on average, for a given height.In addition, you
believe that the muscle/fat tissue composition of male bodies suggests that females will
weigh less, on average, for a given height.To test these theories, you perform the
following regression: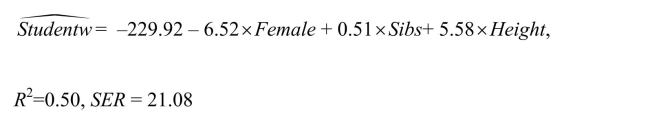 where Studentw is in pounds, Height is in inches, Female takes a value of 1 for females
where Studentw is in pounds, Height is in inches, Female takes a value of 1 for females
and is 0 otherwise, Sibs is the number of siblings.
Interpret the regression results.
at your university, you also asked the students for the number of siblings they have.
Although it was not quite clear to you initially what you would use that variable for, you
construct a new theory that suggests that children who have more siblings come from
poorer families and will have to share the food on the table.Although a friend tells you
that this theory does not pass the "straight-face" test, you decide to hypothesize that peers
with many siblings will weigh less, on average, for a given height.In addition, you
believe that the muscle/fat tissue composition of male bodies suggests that females will
weigh less, on average, for a given height.To test these theories, you perform the
following regression:
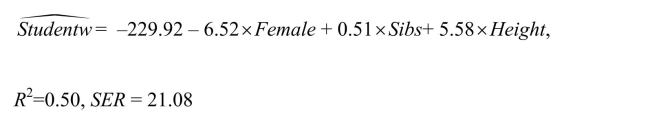 where Studentw is in pounds, Height is in inches, Female takes a value of 1 for females
where Studentw is in pounds, Height is in inches, Female takes a value of 1 for femalesand is 0 otherwise, Sibs is the number of siblings.
Interpret the regression results.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
41
The probability limit of the OLS estimator in the case of omitted variables is given in
your text by the following formula: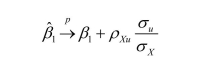 Give an intuitive explanation for two conditions under which the bias will be small.
Give an intuitive explanation for two conditions under which the bias will be small.
your text by the following formula:
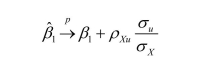 Give an intuitive explanation for two conditions under which the bias will be small.
Give an intuitive explanation for two conditions under which the bias will be small.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
42
For this question, use the California Testscore Data Set and your regression package (a spreadsheet program if necessary). First perform a multiple regression of testscores on a constant, the student-teacher ratio, and the percent of English learners. Record the coefficients. Next, do the following three step procedure instead: first, regress the testscore on a constant and the percent of English learners. Calculate the residuals and store them under the name res YX2 . Second, regress the student-teacher ratio on a constant and the percent of English learners. Calculate the residuals from this regression and store these under the name resXIX2. Finally regress resYX2 on resXIX2 (and a constant, if you wish). Explain intuitively why the simple regression coefficient in the last regression is identical to the regression coefficient on the student-teacher ratio in the multiple regression.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
43
(Requires Statistics background beyond Chapters 2 and 3 ) One way to establish whether or not there is independence between two or more variables is to perform 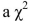 - test on independence between two variables. Explain why multiple regression analysis is a preferable tool to seek a relationship between variables.
- test on independence between two variables. Explain why multiple regression analysis is a preferable tool to seek a relationship between variables.
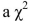 - test on independence between two variables. Explain why multiple regression analysis is a preferable tool to seek a relationship between variables.
- test on independence between two variables. Explain why multiple regression analysis is a preferable tool to seek a relationship between variables.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
44
 in the case of two explanatory variables.Give an intuitive explanations as to why this is
in the case of two explanatory variables.Give an intuitive explanations as to why this isthe case.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
45
(Requires Calculus)For the case of the multiple regression problem with two explanatory
variables, derive the OLS estimator for the intercept and the two slopes.
variables, derive the OLS estimator for the intercept and the two slopes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
46
Your textbook extends the simple regression analysis of Chapters 4 and 5 by adding an
additional explanatory variable, the percent of English learners in school districts (PctEl).
The results are as follows: Explain why you think the coefficient on the student-teacher ratio has changed so
Explain why you think the coefficient on the student-teacher ratio has changed so
dramatically (been more than halved).
additional explanatory variable, the percent of English learners in school districts (PctEl).
The results are as follows:
 Explain why you think the coefficient on the student-teacher ratio has changed so
Explain why you think the coefficient on the student-teacher ratio has changed sodramatically (been more than halved).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
47
One of your peers wants to analyze whether or not participating in varsity sports lowers
or increases the GPA of students.She decides to collect data from 110 male and female
students on their GPA and the number of hours they spend participating in varsity sports.
The coefficient in the simple regression function turns out to be significantly negative,
using the t-statistic and carrying out the appropriate hypothesis test.Upon reflection, she
is concerned that she did not ask the students in her sample whether or not they were
female or male.You point out to her that you are more concerned about the effect of
omitted variables in her regression, such as the incoming SAT score of the students, and
whether or not they are in a major from a high/low grading department.Elaborate on your
argument.
or increases the GPA of students.She decides to collect data from 110 male and female
students on their GPA and the number of hours they spend participating in varsity sports.
The coefficient in the simple regression function turns out to be significantly negative,
using the t-statistic and carrying out the appropriate hypothesis test.Upon reflection, she
is concerned that she did not ask the students in her sample whether or not they were
female or male.You point out to her that you are more concerned about the effect of
omitted variables in her regression, such as the incoming SAT score of the students, and
whether or not they are in a major from a high/low grading department.Elaborate on your
argument.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
48
It is not hard, but tedious, to derive the OLS formulae for the slope coefficient in the
multiple regression case with two explanatory variables.The formula for the first
regression slope is Show that this formula reduces to the slope coefficient for the linear regression model
Show that this formula reduces to the slope coefficient for the linear regression model
with one regressor if the sample correlation between the two explanatory variables is
zero.Given this result, what can you say about the effect of omitting the second
explanatory variable from the regression?
multiple regression case with two explanatory variables.The formula for the first
regression slope is
 Show that this formula reduces to the slope coefficient for the linear regression model
Show that this formula reduces to the slope coefficient for the linear regression modelwith one regressor if the sample correlation between the two explanatory variables is
zero.Given this result, what can you say about the effect of omitting the second
explanatory variable from the regression?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
49
(Requires Calculus)For the case of the multiple regression problem with two explanatory
variables, show that minimizing the sum of squared residuals results in three conditions:
variables, show that minimizing the sum of squared residuals results in three conditions:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
50
(Requires some Calculus) Consider the sample regression function 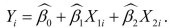 Take the total derivative. Next show that the partial derivative
Take the total derivative. Next show that the partial derivative 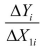 is obtained by holding
is obtained by holding 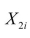 constant, or controlling for
constant, or controlling for 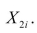
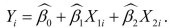 Take the total derivative. Next show that the partial derivative
Take the total derivative. Next show that the partial derivative 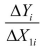 is obtained by holding
is obtained by holding 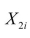 constant, or controlling for
constant, or controlling for 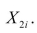

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
51
(Requires Calculus) For the simple linear regression model of Chapter 4 , 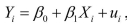 the OLS estimator for the intercept was
the OLS estimator for the intercept was 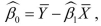 and
and
https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/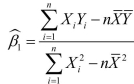 . Intuitively, the OLS estimators for the regression model
. Intuitively, the OLS estimators for the regression model
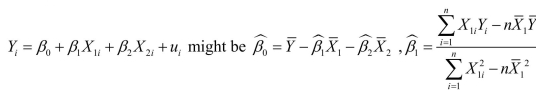 and
and 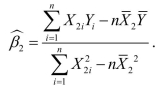
By minimizing the prediction mistakes of the regression model with two explanatory variables, show that this cannot be the case.
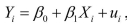 the OLS estimator for the intercept was
the OLS estimator for the intercept was 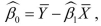 and
andhttps://d2lvgg3v3hfg70.cloudfront.net/TB34225555/
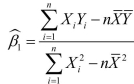 . Intuitively, the OLS estimators for the regression model
. Intuitively, the OLS estimators for the regression model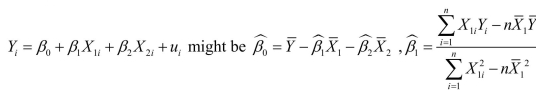 and
and 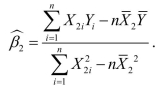
By minimizing the prediction mistakes of the regression model with two explanatory variables, show that this cannot be the case.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
52
(Requires Appendix material) Consider the following population regression function model with two explanatory variables: 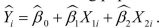
It is easy but tedious to
show that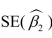 is given by the following formula:
is given by the following formula: 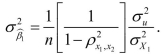 Sketch how
Sketch how
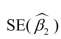 increases with the correlation between
increases with the correlation between 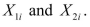
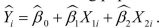
It is easy but tedious to
show that
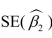 is given by the following formula:
is given by the following formula: 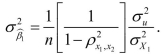 Sketch how
Sketch how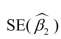 increases with the correlation between
increases with the correlation between 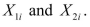

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
53
In the multiple regression with two explanatory variables, show that the TSS can still be
decomposed into the ESS and the RSS.
decomposed into the ESS and the RSS.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck
54
Give at least three examples from macroeconomics and three from microeconomics that
involve specified equations in a multiple regression analysis framework.Indicate in each
case what the expected signs of the coefficients would be and if theory gives you an
indication about the likely size of the coefficients.
involve specified equations in a multiple regression analysis framework.Indicate in each
case what the expected signs of the coefficients would be and if theory gives you an
indication about the likely size of the coefficients.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 54 في هذه المجموعة.
فتح الحزمة
k this deck








