Deck 18: The Theory of Multiple Regression
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/38
العب
ملء الشاشة (f)
Deck 18: The Theory of Multiple Regression
1
The multiple regression model in matrix form can also be written as
A)
B)
C)
D)
A)
B)
C)
D)
2
Minimization of results in
A)
B)
C)
D)
A)
B)
C)
D)
3
The multiple regression model can be written in matrix form as follows: 

D
4
The GLS estimator is defined as 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
5
The difference between the central limit theorems for a scalar and vector-valued random variables is
A)that n approaches infinity in the central limit theorem for scalars only.
B)the conditions on the variances.
C)that single random variables can have an expected value but vectors cannot.
D)the homoskedasticity assumption in the former but not the latter.
A)that n approaches infinity in the central limit theorem for scalars only.
B)the conditions on the variances.
C)that single random variables can have an expected value but vectors cannot.
D)the homoskedasticity assumption in the former but not the latter.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
6
The OLS estimator
A)has the multivariate normal asymptotic distribution in large samples.
B)is t-distributed.
C)has the multivariate normal distribution regardless of the sample size.
D)is F-distributed.
A)has the multivariate normal asymptotic distribution in large samples.
B)is t-distributed.
C)has the multivariate normal distribution regardless of the sample size.
D)is F-distributed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
7
The extended least squares assumptions in the multiple regression model include four assumptions from Chapter 6 are i.i.d. draws from their joint distribution; have nonzero finite fourth moments; there is no perfect multicollinearity). In addition, there are two further assumptions, one of which is
A) heteroskedasticity of the error term.
B) serial correlation of the error term.
C) homoskedasticity of the error term.
D) invertibility of the matrix of regressors.
A) heteroskedasticity of the error term.
B) serial correlation of the error term.
C) homoskedasticity of the error term.
D) invertibility of the matrix of regressors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
8
The assumption that X has full column rank implies that
A)the number of observations equals the number of regressors.
B)binary variables are absent from the list of regressors.
C)there is no perfect multicollinearity.
D)none of the regressors appear in natural logarithm form.
A)the number of observations equals the number of regressors.
B)binary variables are absent from the list of regressors.
C)there is no perfect multicollinearity.
D)none of the regressors appear in natural logarithm form.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
9
The Gauss-Markov theorem for multiple regressions states that the OLS estimator
A)has the smallest variance possible for any linear estimator.
B)is BLUE if the Gauss-Markov conditions for multiple regression hold.
C)is identical to the maximum likelihood estimator.
D)is the most commonly used estimator.
A)has the smallest variance possible for any linear estimator.
B)is BLUE if the Gauss-Markov conditions for multiple regression hold.
C)is identical to the maximum likelihood estimator.
D)is the most commonly used estimator.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
10
The heteroskedasticity-robust estimator of is obtained
A)
B) by replacing the population moments in its definition by the identity matrix.
C) from feasible GLS estimation.
D) by replacing the population moments in its definition by sample moments.
A)
B) by replacing the population moments in its definition by the identity matrix.
C) from feasible GLS estimation.
D) by replacing the population moments in its definition by sample moments.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
11
One implication of the extended least squares assumptions in the multiple regression model is that 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
12
The formulation to test a hypotheses
A) allows for restrictions involving both multiple regression coefficients and single regression coefficients.
B) is F -distributed in large samples.
C) allows only for restrictions involving multiple regression coefficients.
D) allows for testing linear as well as nonlinear hypotheses.
A) allows for restrictions involving both multiple regression coefficients and single regression coefficients.
B) is F -distributed in large samples.
C) allows only for restrictions involving multiple regression coefficients.
D) allows for testing linear as well as nonlinear hypotheses.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
13
In the case when the errors are homoskedastic and normally distributed, conditional on X, then 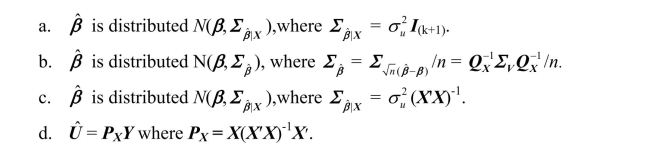
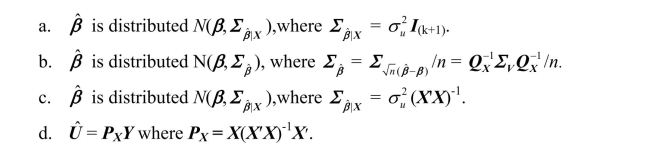

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
14
A joint hypothesis that is linear in the coefficients and imposes a number of restrictions can be written as 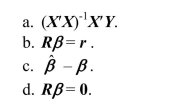
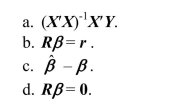

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
15
Let there be q joint hypothesis to be tested. Then the dimension of r in the expression is
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
16
The GLS assumptions include all of the following, with the exception of 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
17
The linear multiple regression model can be represented in matrix notation as where X is of order n x(k+1) . k represents the number of
A) regressors.
B) observations.
C) regressors excluding the "constant" regressor for the intercept.
D) unknown regression coefficients
A) regressors.
B) observations.
C) regressors excluding the "constant" regressor for the intercept.
D) unknown regression coefficients

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
18
The Gauss-Markov theorem for multiple regression proves that 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
19
One of the properties of the OLS estimator is 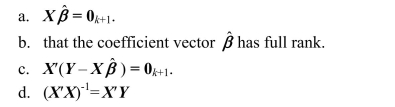
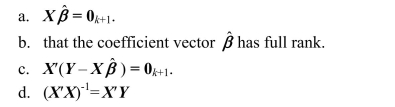

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
20
A) cannot be calculated since the population parameter is unknown.
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
21
Define the GLS estimator and discuss its properties when  is known. Why is this estimator sometimes called infeasible GLS? What happens when
is known. Why is this estimator sometimes called infeasible GLS? What happens when  is unknown? What would the
is unknown? What would the 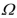 matrix look like for the case of independent sampling with heteroskedastic errors, where
matrix look like for the case of independent sampling with heteroskedastic errors, where 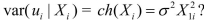
Since the inverse of the error variancecovariance matrix is needed to compute the GLS estimator, find https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/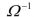 . The textbook shows that the original model
. The textbook shows that the original model 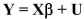
will be transformed into where
where 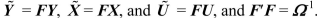
Find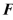 in the above case, and describe what effect the transformation has on the original data.
in the above case, and describe what effect the transformation has on the original data.
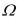 is known. Why is this estimator sometimes called infeasible GLS? What happens when
is known. Why is this estimator sometimes called infeasible GLS? What happens when 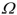 is unknown? What would the
is unknown? What would the 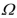 matrix look like for the case of independent sampling with heteroskedastic errors, where
matrix look like for the case of independent sampling with heteroskedastic errors, where 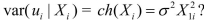
Since the inverse of the error variancecovariance matrix is needed to compute the GLS estimator, find https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/
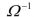 . The textbook shows that the original model
. The textbook shows that the original model 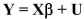
will be transformed into
 where
where 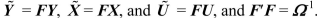
Find
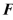 in the above case, and describe what effect the transformation has on the original data.
in the above case, and describe what effect the transformation has on the original data.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
22
Write the following four restrictions in the form 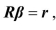 where the hypotheses are to be tested simultaneously.
where the hypotheses are to be tested simultaneously.
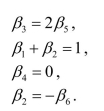
Can you write the following restriction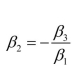 in the same format? Why not?
in the same format? Why not?
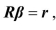 where the hypotheses are to be tested simultaneously.
where the hypotheses are to be tested simultaneously.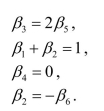
Can you write the following restriction
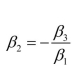 in the same format? Why not?
in the same format? Why not?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
23
In Chapter 10 of your textbook, panel data estimation was introduced.Panel data consist
of observations on the same n entities at two or more time periods T.For two variables,
you have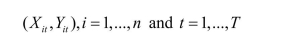 where n could be the U.S.states.The example in Chapter 10 used annual data from 1982
where n could be the U.S.states.The example in Chapter 10 used annual data from 1982
to 1988 for the fatality rate and beer taxes.Estimation by OLS, in essence, involved
"stacking" the data.
(a)What would the variance-covariance matrix of the errors look like in this case if you
allowed for homoskedasticity-only standard errors? What is its order? Use an example of
a linear regression with one regressor of 4 U.S.states and 3 time periods.
of observations on the same n entities at two or more time periods T.For two variables,
you have
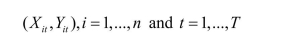 where n could be the U.S.states.The example in Chapter 10 used annual data from 1982
where n could be the U.S.states.The example in Chapter 10 used annual data from 1982to 1988 for the fatality rate and beer taxes.Estimation by OLS, in essence, involved
"stacking" the data.
(a)What would the variance-covariance matrix of the errors look like in this case if you
allowed for homoskedasticity-only standard errors? What is its order? Use an example of
a linear regression with one regressor of 4 U.S.states and 3 time periods.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
24
 q = 5 +3 p - 2 y
q = 5 +3 p - 2 yq = 10 - p + 10 y
p = 6 y

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
25
The leading example of sampling schemes in econometrics that do not result in independent observations is
A)cross-sectional data.
B)experimental data.
C)the Current Population Survey.
D)when the data are sampled over time for the same entity.
A)cross-sectional data.
B)experimental data.
C)the Current Population Survey.
D)when the data are sampled over time for the same entity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
26
Using the model 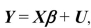 and the extended least squares assumptions, derive the OLS estimator https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/
and the extended least squares assumptions, derive the OLS estimator https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/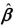 . Discuss the conditions under which
. Discuss the conditions under which  is invertible.
is invertible.
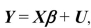 and the extended least squares assumptions, derive the OLS estimator https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/
and the extended least squares assumptions, derive the OLS estimator https://d2lvgg3v3hfg70.cloudfront.net/TB34225555/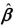 . Discuss the conditions under which
. Discuss the conditions under which  is invertible.
is invertible.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
27
Consider the multiple regression model from Chapter 5, where k = 2 and the assumptions
of the multiple regression model hold.
(a)Show what the X matrix and the vector would look like in this case.
vector would look like in this case.
of the multiple regression model hold.
(a)Show what the X matrix and the
 vector would look like in this case.
vector would look like in this case.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
28
Prove that under the extended least squares assumptions the OLS estimator 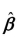 is unbiased and that its variance-covariance matrix is
is unbiased and that its variance-covariance matrix is 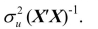
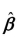 is unbiased and that its variance-covariance matrix is
is unbiased and that its variance-covariance matrix is 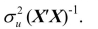

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
29
Assume that the data looks as follows: 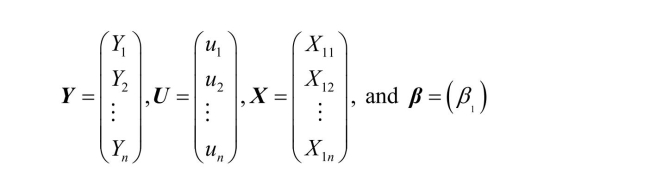
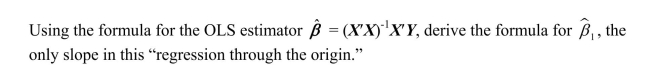

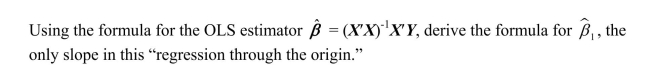

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
30
The presence of correlated error terms creates problems for inference based on OLS. These can be overcome by
A)using HAC standard errors.
B)using heteroskedasticity-robust standard errors.
C)reordering the observations until the correlation disappears.
D)using homoskedasticity-only standard errors.
A)using HAC standard errors.
B)using heteroskedasticity-robust standard errors.
C)reordering the observations until the correlation disappears.
D)using homoskedasticity-only standard errors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
31
The GLS estimator
A)is always the more efficient estimator when compared to OLS.
B)is the OLS estimator of the coefficients in a transformed model, where the errors of the transformed model satisfy the Gauss-Markov conditions.
C)cannot handle binary variables, since some of the transformations require division by one of the regressors.
D)produces identical estimates for the coefficients, but different standard errors.
A)is always the more efficient estimator when compared to OLS.
B)is the OLS estimator of the coefficients in a transformed model, where the errors of the transformed model satisfy the Gauss-Markov conditions.
C)cannot handle binary variables, since some of the transformations require division by one of the regressors.
D)produces identical estimates for the coefficients, but different standard errors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
32
In order for a matrix A to have an inverse, its determinant cannot be zero.Derive the
determinant of the following matrices: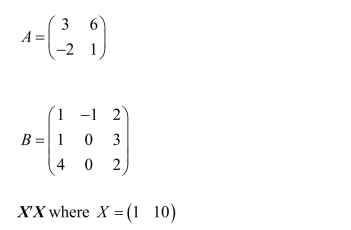
determinant of the following matrices:
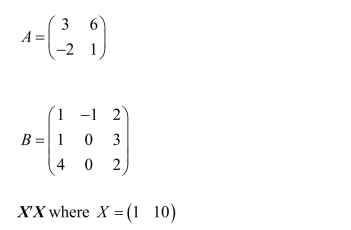

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
33
Your textbook derives the OLS estimator as 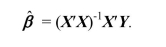 Show that the estimator does not exist if there are fewer observations than the number of
Show that the estimator does not exist if there are fewer observations than the number of
explanatory variables, including the constant.What is the rank of X′X in this case?
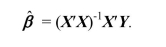 Show that the estimator does not exist if there are fewer observations than the number of
Show that the estimator does not exist if there are fewer observations than the number ofexplanatory variables, including the constant.What is the rank of X′X in this case?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
34
Given the following matrices 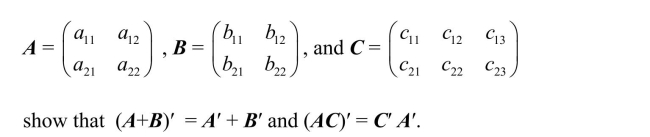
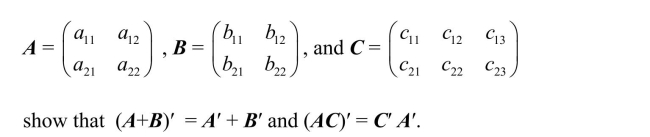

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
35
For the OLS estimator 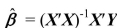 to exist,
to exist, 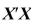 must be invertible. This is the case when
must be invertible. This is the case when 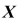 has full rank. What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that
has full rank. What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that 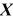 could have rank n ? What would be the rank of
could have rank n ? What would be the rank of 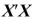 in the case
in the case  Explain intuitively why the OLS estimator does not exist in that situation.
Explain intuitively why the OLS estimator does not exist in that situation.
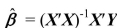 to exist,
to exist, 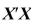 must be invertible. This is the case when
must be invertible. This is the case when 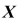 has full rank. What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that
has full rank. What is the rank of a matrix? What is the rank of the product of two matrices? Is it possible that 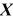 could have rank n ? What would be the rank of
could have rank n ? What would be the rank of 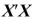 in the case
in the case  Explain intuitively why the OLS estimator does not exist in that situation.
Explain intuitively why the OLS estimator does not exist in that situation.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
36
An estimator of is said to be linear if
A) it can be estimated by least squares.
B) it is a linear function of
C) there are homoskedasticity-only errors.
D) it is a linear function of
A) it can be estimated by least squares.
B) it is a linear function of
C) there are homoskedasticity-only errors.
D) it is a linear function of

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
37
Give several economic examples of how to test various joint linear hypotheses using matrix notation. Include specifications of 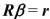 where you test for (i) all coefficients other than the constant being zero, (ii) a subset of coefficients being zero, and (iii) equality of coefficients. Talk about the possible distributions involved in finding critical values for your hypotheses.
where you test for (i) all coefficients other than the constant being zero, (ii) a subset of coefficients being zero, and (iii) equality of coefficients. Talk about the possible distributions involved in finding critical values for your hypotheses.
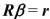 where you test for (i) all coefficients other than the constant being zero, (ii) a subset of coefficients being zero, and (iii) equality of coefficients. Talk about the possible distributions involved in finding critical values for your hypotheses.
where you test for (i) all coefficients other than the constant being zero, (ii) a subset of coefficients being zero, and (iii) equality of coefficients. Talk about the possible distributions involved in finding critical values for your hypotheses.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck
38
Write an essay on the difference between the OLS estimator and the GLS estimator.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 38 في هذه المجموعة.
فتح الحزمة
k this deck








