Deck 10: Radicals, Radical Functions, and Rational Exponents
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/102
العب
ملء الشاشة (f)
Deck 10: Radicals, Radical Functions, and Rational Exponents
1
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)
2
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)
3
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)
4
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
5
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
6
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
7
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
8
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
9
Solve the problem.
A deposit of $7000 is made in an account that earns 7.2% interest compounded quarterly. The balance in the account after n quarters is given by the sequence Find the balance in the account after four years by computing a16
A) $4087.38
B) $5321.38
C) $9312.42
D) $7517.77
A deposit of $7000 is made in an account that earns 7.2% interest compounded quarterly. The balance in the account after n quarters is given by the sequence Find the balance in the account after four years by computing a16
A) $4087.38
B) $5321.38
C) $9312.42
D) $7517.77

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
10
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
11
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
12
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
13
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
14
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
15
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
16
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
17
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
18
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
19
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
20
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
21
Find the indicated sum.
A) 32
B) 60
C) 56
D) 48
A) 32
B) 60
C) 56
D) 48

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
22
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
23
Find the indicated sum.
A)
B)
C) 54
D)
A)
B)
C) 54
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
24
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
25
Find the indicated sum.
A) 48
B) 36
C) 74
D) 95
A) 48
B) 36
C) 74
D) 95

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the indicated sum.
A) 6
B) 18
C) 3
D) 10
A) 6
B) 18
C) 3
D) 10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
27
Find the indicated sum.
A) 14
B) 22
C) 44
D) 30
A) 14
B) 22
C) 44
D) 30

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
28
Find the indicated sum.
A) 56
B) 38
C) 60
D) 27
A) 56
B) 38
C) 60
D) 27

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
29
Find the indicated sum.
A) 72
B) 84
C) 540
D) 588
A) 72
B) 84
C) 540
D) 588

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the indicated sum.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
31
Find the indicated sum.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
32
Write the first four terms of the sequence whose general term is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
33
Find the indicated sum.
A) -14
B) 6
C) 2
D) 14
A) -14
B) 6
C) 2
D) 14

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
34
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find the indicated sum.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
36
Find the indicated sum.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
37
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
38
Find the indicated sum.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
39
Find the indicated sum.
A) 18
B) 14
C) 30
D) 20
A) 18
B) 14
C) 30
D) 20

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
40
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
41
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
42
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
a1 = -1.7, d = -1.5
A) -1.7, -3.2, -4.7, -6.2, -7.7
B) -1.7, -0.2, 1.3, 2.8, 4.3
C) -0.2, 1.3, 2.8, 4.3, 5.8
D) -3.2, -4.7, -6.2, -7.7, -9.2
a1 = -1.7, d = -1.5
A) -1.7, -3.2, -4.7, -6.2, -7.7
B) -1.7, -0.2, 1.3, 2.8, 4.3
C) -0.2, 1.3, 2.8, 4.3, 5.8
D) -3.2, -4.7, -6.2, -7.7, -9.2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
43
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
a1 = 5; d = -1
A) 5, 4, 3, 2, 1
B) 4, 3, 2, 1, 0
C) 5, 4, 2, 2, 1
D) 6, 5, 4, 3, 2
a1 = 5; d = -1
A) 5, 4, 3, 2, 1
B) 4, 3, 2, 1, 0
C) 5, 4, 2, 2, 1
D) 6, 5, 4, 3, 2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
44
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the common difference for the arithmetic sequence.
583, 588, 593, 598, . . .
A) 583
B) 5
C) -583
D) -5
583, 588, 593, 598, . . .
A) 583
B) 5
C) -583
D) -5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
46
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
47
Solve the problem.
The finite sequence whose general term is , where models the total operating costs, in millions of dollars, for a company for nine consecutive years.
Find
A) $23.4 million
B) $32.65 million
C) $29.05 million
D) $26.12 million
The finite sequence whose general term is , where models the total operating costs, in millions of dollars, for a company for nine consecutive years.
Find
A) $23.4 million
B) $32.65 million
C) $29.05 million
D) $26.12 million

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
48
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
49
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
a1 = 1; d = 2
A) 3, 5, 7, 9, 11
B) 0, 1, 3, 5, 7
C) 1, 2, 3, 4, 5
D) 1, 3, 5, 7, 9
a1 = 1; d = 2
A) 3, 5, 7, 9, 11
B) 0, 1, 3, 5, 7
C) 1, 2, 3, 4, 5
D) 1, 3, 5, 7, 9

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
50
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
51
Find the common difference for the arithmetic sequence.
2, -1, -4, -7, . . .
A) 9
B) -3
C) -9
D) -6
2, -1, -4, -7, . . .
A) 9
B) -3
C) -9
D) -6

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
52
Solve the problem.
The bar graph below shows a company's yearly profits from 2003 to 2011. Let an represent the company's profit, in millions, in year n, where n = 1 corresponds to 2003, n = 2 corresponds to 2004, and so on.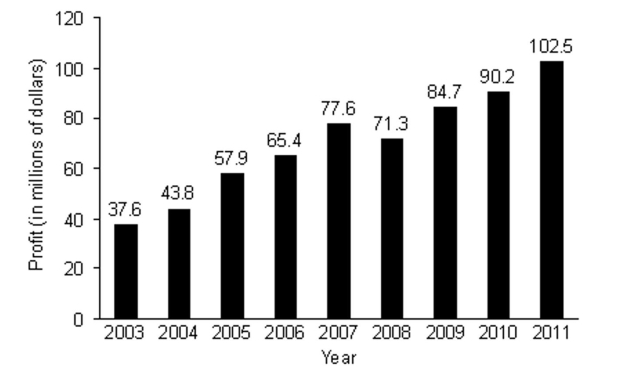
A) $505.8 million
B) $549.6 million
C) $167.9 million
D) $491.7 million
The bar graph below shows a company's yearly profits from 2003 to 2011. Let an represent the company's profit, in millions, in year n, where n = 1 corresponds to 2003, n = 2 corresponds to 2004, and so on.

A) $505.8 million
B) $549.6 million
C) $167.9 million
D) $491.7 million

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
53
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
a1 = 18; d = -4
A) 0, 18, 14, 10, 6
B) 22, 17, 12, 7, 2
C) 18, 14, 10, 6, 2
D) -18, -14, -10, -6, -2
a1 = 18; d = -4
A) 0, 18, 14, 10, 6
B) 22, 17, 12, 7, 2
C) 18, 14, 10, 6, 2
D) -18, -14, -10, -6, -2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
54
Write the first five terms of the arithmetic sequence with the given first term, a1, and common difference, d.
a1 = -36; d = 9
A) 0, -9, -18, -27, -36
B) -18, -9, 0, 9, 18
C) -18, -27, -36, -45, -54
D) -36, -27, -18, -9, 0
a1 = -36; d = 9
A) 0, -9, -18, -27, -36
B) -18, -9, 0, 9, 18
C) -18, -27, -36, -45, -54
D) -36, -27, -18, -9, 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
55
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the common difference for the arithmetic sequence.
3, 5, 7, 9, . . .
A) 2
B) -2
C) -6
D) 6
3, 5, 7, 9, . . .
A) 2
B) -2
C) -6
D) 6

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
57
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
58
Express the sum using summation notation. Use a lower limit of summation, not necessarily 1, and k for the index of
summation.
A)
B)
C)
D)
summation.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find the common difference for the arithmetic sequence.
7, 9, 11, 13, . . .
A) 6
B) 2
C) 1.5
D) 7
7, 9, 11, 13, . . .
A) 6
B) 2
C) 1.5
D) 7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
60
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
61
Write out the first three terms and the last term of the arithmetic sequence.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
62
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
2 , 6 , 10 , 14 , 18 , . . .
A)
B)
C)
D)
the 20th term of the sequence.
2 , 6 , 10 , 14 , 18 , . . .
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
63
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
Find 1 + 3 + 5 + 7 + . . ., the sum of the first 55 positive odd integers.
A) 2970
B) 3025
C) 3029
D) 2966
Find 1 + 3 + 5 + 7 + . . ., the sum of the first 55 positive odd integers.
A) 2970
B) 3025
C) 3029
D) 2966

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
64
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
Find a 17 when a1 = -4 , d = - 1 .
A) 12
B) 13
C) - 20
D) - 21
with the given first term, a1, and common difference, d.
Find a 17 when a1 = -4 , d = - 1 .
A) 12
B) 13
C) - 20
D) - 21

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
65
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
Find a90 when a1 = -14, d = -5.
A) -464
B) 431
C) -459
D) 436
with the given first term, a1, and common difference, d.
Find a90 when a1 = -14, d = -5.
A) -464
B) 431
C) -459
D) 436

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
66
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
A)
B)
C)
D)
the 20th term of the sequence.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
67
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
Find a11 when a1 = 20, d = -6.
A) 80
B) -46
C) -40
D) -60
with the given first term, a1, and common difference, d.
Find a11 when a1 = 20, d = -6.
A) 80
B) -46
C) -40
D) -60

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
68
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
Find the sum of the first eight terms of the arithmetic sequence: 10, 15, 20, . . . .
A) 220
B) 45
C) 120
D) 440
Find the sum of the first eight terms of the arithmetic sequence: 10, 15, 20, . . . .
A) 220
B) 45
C) 120
D) 440

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
69
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
-21, -26 , -31, -36, . . .
A)
B)
C)
D)
the 20th term of the sequence.
-21, -26 , -31, -36, . . .
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
70
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
Find the sum of the first four terms of the arithmetic sequence: -3, -15, -27, . . . .
A) 84
B) -60
C) - 84
D) -45
Find the sum of the first four terms of the arithmetic sequence: -3, -15, -27, . . . .
A) 84
B) -60
C) - 84
D) -45

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
71
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
27, 18 , 9, 0, . . .
A)
B)
C)
D)
the 20th term of the sequence.
27, 18 , 9, 0, . . .
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
72
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
Find a 32 when a1 = -3 , d = 3 .
A) 93
B) -96
C) -99
D) 90
with the given first term, a1, and common difference, d.
Find a 32 when a1 = -3 , d = 3 .
A) 93
B) -96
C) -99
D) 90

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
73
Solve the problem.
To train for a race, Will begins by jogging 11 minutes one day per week. He increases his jogging time by 3 minutes each week. Write the general term of this arithmetic sequence, and find how many weeks it takes for
Him to reach a jogging time of one hour.
A) weeks
B) weeks
C) weeks
D) weeks
To train for a race, Will begins by jogging 11 minutes one day per week. He increases his jogging time by 3 minutes each week. Write the general term of this arithmetic sequence, and find how many weeks it takes for
Him to reach a jogging time of one hour.
A) weeks
B) weeks
C) weeks
D) weeks

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
74
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
Find the sum of the first 70 terms of the arithmetic sequence: 1, 8, 15, 22, . . . .
A) 16,733
B) 15,990
C) 17,220
D) 16,975
Find the sum of the first 70 terms of the arithmetic sequence: 1, 8, 15, 22, . . . .
A) 16,733
B) 15,990
C) 17,220
D) 16,975

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
75
Use the formula for the general term (the nth term) of an arithmetic sequence to find the indicated term of the sequence
with the given first term, a1, and common difference, d.
Find a8 when a1 = -8 , d = -5 .
A) -43
B) 27
C) -48
D) 32
with the given first term, a1, and common difference, d.
Find a8 when a1 = -8 , d = -5 .
A) -43
B) 27
C) -48
D) 32

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
76
Solve the problem.
Jacie is considering a job that offers a monthly starting salary of $3000 and guarantees her a monthly raise of $130 during her first year on the job. Find the general term of this arithmetic sequence and her monthly salary at
The end of her first year.
A)
B)
C)
D)
Jacie is considering a job that offers a monthly starting salary of $3000 and guarantees her a monthly raise of $130 during her first year on the job. Find the general term of this arithmetic sequence and her monthly salary at
The end of her first year.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
77
Solve the problem.
The population of a town is increasing by 400 inhabitants each year. If its current population is 29,089 and this trend continues, what would its population be in 8 years?
A) 232,600 inhabitants
B) 32,289 inhabitants
C) 465,200 inhabitants
D) 31,889 inhabitants
The population of a town is increasing by 400 inhabitants each year. If its current population is 29,089 and this trend continues, what would its population be in 8 years?
A) 232,600 inhabitants
B) 32,289 inhabitants
C) 465,200 inhabitants
D) 31,889 inhabitants

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
78
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
A)
B)
C)
D)
the 20th term of the sequence.
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
79
Use the partial sum formula to find the partial sum of the given arithmetic sequence.
Find the sum of the odd integers between 24 and 66.
A) 900
B) 990
C) 945
D) 1035
Find the sum of the odd integers between 24 and 66.
A) 900
B) 990
C) 945
D) 1035

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck
80
Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for an to find a20,
the 20th term of the sequence.
3 , 12 , 21 , 30 , 39 , . . .
A)
B)
C)
D)
the 20th term of the sequence.
3 , 12 , 21 , 30 , 39 , . . .
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 102 في هذه المجموعة.
فتح الحزمة
k this deck








