Deck 5: Sampling Distributions
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/52
العب
ملء الشاشة (f)
Deck 5: Sampling Distributions
1
The probability distribution shown below describes a population of measurements.
Suppose that we took repeated random samples of observations from the population described above. Find the expected value of the sampling distribution of the sample mean.
A) 2
B) 0
C) 1
D) 3
E) 4
Suppose that we took repeated random samples of observations from the population described above. Find the expected value of the sampling distribution of the sample mean.
A) 2
B) 0
C) 1
D) 3
E) 4
2
2
The sampling distribution of the sample mean is shown below. 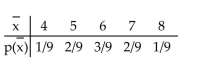 Find the expected value of the sampling distribution of the sample mean.
Find the expected value of the sampling distribution of the sample mean.
A) 5
B) 4
C) 6
D) 7
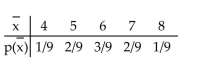 Find the expected value of the sampling distribution of the sample mean.
Find the expected value of the sampling distribution of the sample mean.A) 5
B) 4
C) 6
D) 7
C
3
Which of the following describes what the property of unbiasedness means?
A) The shape of the sampling distribution is approximately normally distributed.
B) The sampling distribution in question has the smallest variation of all possible sampling distributions.
C) The center of the sampling distribution is found at the population standard deviation.
D) The center of the sampling distribution is found at the population parameter that is being estimated.
A) The shape of the sampling distribution is approximately normally distributed.
B) The sampling distribution in question has the smallest variation of all possible sampling distributions.
C) The center of the sampling distribution is found at the population standard deviation.
D) The center of the sampling distribution is found at the population parameter that is being estimated.
D
4
Consider the population described by the probability distribution below.
a. Find .
b. Find the sampling distribution of the sample mean for a random sample of measurements from the distribution.
c. Show that is an unbiased estimator of .
a. Find .
b. Find the sampling distribution of the sample mean for a random sample of measurements from the distribution.
c. Show that is an unbiased estimator of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
5
The amount of time it takes a student to walk from her home to class has a skewed right distribution with a mean of 10 minutes and a standard deviation of 1.6 minutes. If times were collected from 40 randomly selected walks, describe the sampling distribution of the sample mean time.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
6
The probability distribution shown below describes a population of measurements.
Suppose that we took repeated random samples of observations from the population described above. Which of the following would represent the sampling distribution of the sample mean?
A)
B)
C)
Suppose that we took repeated random samples of observations from the population described above. Which of the following would represent the sampling distribution of the sample mean?
A)
B)
C)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
7
A random sample of size n is to be drawn from a population with What size sample would be necessary in order to reduce the standard error to 10?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
8
Consider the probability distribution shown here.
Let be the sample mean for random samples of measurements from this distribution. Find and .
Let be the sample mean for random samples of measurements from this distribution. Find and .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
9
Consider the population described by the probability distribution below. a. Find .
b. Find the sampling distribution of the sample mean for a random sample of measurements from this distribution.
c. Find the sampling distribution of the sample median for a random sample of observations from this population.
d. Show that both the mean and the median are unbiased estimators of for this population.
e. Find the variances of the sampling distributions of the sample mean and the sample median.
f. Which estimator would you use to estimate ? Why?
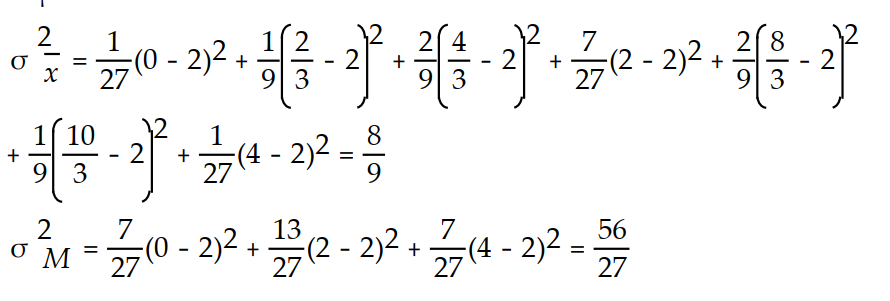
b. Find the sampling distribution of the sample mean for a random sample of measurements from this distribution.
c. Find the sampling distribution of the sample median for a random sample of observations from this population.
d. Show that both the mean and the median are unbiased estimators of for this population.
e. Find the variances of the sampling distributions of the sample mean and the sample median.
f. Which estimator would you use to estimate ? Why?
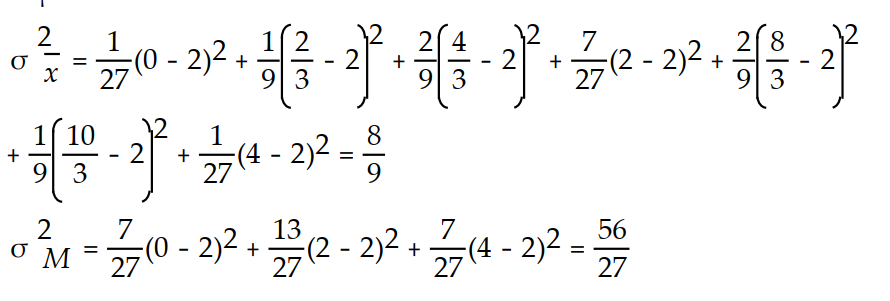

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
10
Suppose a random sample of measurements is selected from a population with mean and standard deviation . Find the -score corresponding to a value of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
11
The weight of corn chips dispensed into a 10-ounce bag by the dispensing machine has been identified as possessing a normal distribution with a mean of 10.5 ounces and a standard deviation of .2 ounce. Suppose 100 bags of chips are randomly selected. Find the probability that the mean weight of these 100 bags exceeds 10.45 ounces.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
12
Which of the following describes what the property of minimum variance means?
A) The sampling distribution in question has the smallest variation of all possible unbiased sampling distributions.
B) The center of the sampling distribution is found at the population standard deviation.
C) The shape of the sampling distribution is approximately normally distributed.
D) The center of the sampling distribution is found at the population parameter that is being estimated.
A) The sampling distribution in question has the smallest variation of all possible unbiased sampling distributions.
B) The center of the sampling distribution is found at the population standard deviation.
C) The shape of the sampling distribution is approximately normally distributed.
D) The center of the sampling distribution is found at the population parameter that is being estimated.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
13
Consider the population described by the probability distribution below.
a. Find .
b. Find the sampling distribution of the sample variance for a random sample of measurements from the distribution.
c. Show that is an unbiased estimator of .
a. Find .
b. Find the sampling distribution of the sample variance for a random sample of measurements from the distribution.
c. Show that is an unbiased estimator of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
14
The probability distribution shown below describes a population of measurements that can assume values of 5, 9, 13, and 17, each of which occurs with the same frequency:
Find . Then consider taking samples of measurements and calculating for each sample. Find the expected value, , of .
Find . Then consider taking samples of measurements and calculating for each sample. Find the expected value, , of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
15


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
16
The probability distribution shown below describes a population of measurements that can assume values of 2, 5, 8, and 11, each of which occurs with the same frequency:
Consider taking samples of measurements and calculating for each sample. Construct the probability histogram for the sampling distribution of .
Consider taking samples of measurements and calculating for each sample. Construct the probability histogram for the sampling distribution of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
17
Suppose students' ages follow a skewed right distribution with a mean of 23 years old and a standard deviation of 4 years. If we randomly sample 200 students, which of the following
Statements about the sampling distribution of the sample mean age is incorrect?
A) The standard deviation of the sampling distribution is equal to 4 years.
B) The mean of the sampling distribution is approximately 23 years old.
C) The shape of the sampling distribution is approximately normal.
D) All of the above statements are correct.
Statements about the sampling distribution of the sample mean age is incorrect?
A) The standard deviation of the sampling distribution is equal to 4 years.
B) The mean of the sampling distribution is approximately 23 years old.
C) The shape of the sampling distribution is approximately normal.
D) All of the above statements are correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
18
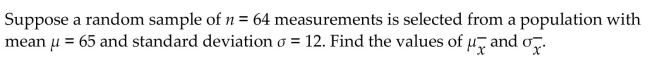

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
19
Consider the population described by the probability distribution below.
The random variable is observed twice. The observations are independent. The different samples of size 2 and their probabilities are shown below.
Find the sampling distribution of the sample mean .
The random variable is observed twice. The observations are independent. The different samples of size 2 and their probabilities are shown below.
Find the sampling distribution of the sample mean .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
20
The length of time a traffic signal stays green (nicknamed the "green time") at a particular intersection follows a normal probability distribution with a mean of 200 seconds and the standard
Deviation of 10 seconds. Use this information to answer the following questions. Which of the
Following describes the derivation of the sampling distribution of the sample mean?
A) The means of a large number of samples of size n randomly selected from the population of "green times" are calculated and their probabilities are plotted.
B) The standard deviations of a large number of samples of size n randomly selected from the population of "green times" are calculated and their probabilities are plotted.
C) A single sample of sufficiently large size is randomly selected from the population of "green times" and its probability is determined.
D) The mean and median of a large randomly selected sample of "green times" are calculated. Depending on whether or not the population of "green times" is normally distributed, either
The mean or the median is chosen as the best measurement of center.
Deviation of 10 seconds. Use this information to answer the following questions. Which of the
Following describes the derivation of the sampling distribution of the sample mean?
A) The means of a large number of samples of size n randomly selected from the population of "green times" are calculated and their probabilities are plotted.
B) The standard deviations of a large number of samples of size n randomly selected from the population of "green times" are calculated and their probabilities are plotted.
C) A single sample of sufficiently large size is randomly selected from the population of "green times" and its probability is determined.
D) The mean and median of a large randomly selected sample of "green times" are calculated. Depending on whether or not the population of "green times" is normally distributed, either
The mean or the median is chosen as the best measurement of center.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
21
The ideal estimator has the greatest variance among all unbiased estimators.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
22


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
23
If is a good estimator for µ, then we expect the values of x to cluster around µ.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
24
One year, the distribution of salaries for professional sports players had mean $1.6 million and standard deviation $0.7 million. Suppose a sample of 100 major league players was taken. Find the approximate probability that the average salary of the 100 players that year exceeded $1.1 million.
A) approximately 1
B) .2357
C) .7357
D) approximately 0
A) approximately 1
B) .2357
C) .7357
D) approximately 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
25
The probability of success, p, in a binomial experiment is a parameter, while the mean and standard deviation, µ and ?, are statistics.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
26
The Central Limit Theorem guarantees that the population is normal whenever n is sufficiently
large.
large.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
27
When estimating the population mean, the sample mean is always a better estimate than the sample median.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
28
Which of the following does the Central Limit Theorem allow us to disregard when working with the sampling distribution of the sample mean?
A) The mean of the population distribution.
B) The shape of the population distribution.
C) The standard deviation of the population distribution.
D) All of the above can be disregarded when the Central Limit Theorem is used.
A) The mean of the population distribution.
B) The shape of the population distribution.
C) The standard deviation of the population distribution.
D) All of the above can be disregarded when the Central Limit Theorem is used.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
29
The Central Limit Theorem states that the sampling distribution of the sample mean is approximately normal under certain conditions. Which of the following is a necessary condition for the Central Limit Theorem to be used?
A) The population from which we are sampling must be normally distributed.
B) The population from which we are sampling must not be normally distributed.
C) The population size must be large .
D) The sample size must be large .
A) The population from which we are sampling must be normally distributed.
B) The population from which we are sampling must not be normally distributed.
C) The population size must be large .
D) The sample size must be large .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
30
The sample mean, , is a statistic.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
31
The average score of all golfers for a particular course has a mean of 66 and a standard deviation of 3.5. Suppose 49 golfers played the course today. Find the probability that the average score of the 49 golfers exceeded 67.
A) .0228
B) .3707
C) .1293
D) .4772
A) .0228
B) .3707
C) .1293
D) .4772

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
32
Which of the following statements about the sampling distribution of the sample mean is incorrect?
A) The sampling distribution is approximately normal whenever the sample size is sufficiently large (n ≥ 30).
B) The standard deviation of the sampling distribution is σ.
C) The mean of the sampling distribution is µ.
D) The sampling distribution is generated by repeatedly taking samples of size n and computing the sample means.
A) The sampling distribution is approximately normal whenever the sample size is sufficiently large (n ≥ 30).
B) The standard deviation of the sampling distribution is σ.
C) The mean of the sampling distribution is µ.
D) The sampling distribution is generated by repeatedly taking samples of size n and computing the sample means.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
33
The Central Limit Theorem is considered powerful in statistics because __________.
A) it works for any population distribution provided the sample size is sufficiently large
B) it works for any sample provided the population distribution is known
C) it works for any population distribution provided the population mean is known
D) it works for any sample size provided the population is normal
A) it works for any population distribution provided the sample size is sufficiently large
B) it works for any sample provided the population distribution is known
C) it works for any population distribution provided the population mean is known
D) it works for any sample size provided the population is normal

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
34
As the sample size gets larger, the standard error of the sampling distribution of the sample mean gets larger as well.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
35
The sampling distribution of a sample statistic calculated from a sample of n measurements is the probability distribution of the statistic.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
36
Consider the population described by the probability distribution below.
a. Find .
b. Find the sampling distribution of the sample median for a random sample of observations from
this population.
c. Show that the median is an unbiased estimator of .
a. Find .
b. Find the sampling distribution of the sample median for a random sample of observations from
this population.
c. Show that the median is an unbiased estimator of .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
37

A) approximately normal; 0.32, 0.0005
B) approximately normal; 0.32, 0.023
C) skewed right; 128, 9.33
D) skewed right; 0.32, 0.023

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
38
In most situations, the true mean and standard deviation are unknown quantities that have to be estimated.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
39
A statistic is biased if the mean of the sampling distribution is equal to the parameter it is intended
to estimate.
to estimate.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
40
A point estimator of a population parameter is a rule or formula which tells us how to use sample
data to calculate a single number that can be used as an estimate of the population parameter.
data to calculate a single number that can be used as an estimate of the population parameter.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
41

A) .92; .011
B) .92; .003
C) .08; .011
D) .08; .003

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
42
Sample statistics are random variables, because different samples can lead to different values of the sample statistics.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
43
The weight of corn chips dispensed into a 14-ounce bag by the dispensing machine has been identified as possessing a normal distribution with a mean of 14.5 ounces and a standard deviation of 0.2 ounce. Suppose 100 bags of chips are randomly selected. Find the probability that the mean weight of these 100 bags exceeds 14.6 ounces.
A) .3085
B) .6915
C) .1915
D) approximately 0
A) .3085
B) .6915
C) .1915
D) approximately 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
44
The number of cars running a red light in a day, at a given intersection, possesses a distribution with a mean of 1.7 cars and a standard deviation of 5. The number of cars running the red light was observed on 100 randomly chosen days and the mean number of cars calculated. Describe the
Sampling distribution of the sample mean.
A) approximately normal with mean and standard deviation
B) shape unknown with mean and standard deviation
C) shape unknown with mean and standard deviation
D) approximately normal with mean and standard deviation
Sampling distribution of the sample mean.
A) approximately normal with mean and standard deviation
B) shape unknown with mean and standard deviation
C) shape unknown with mean and standard deviation
D) approximately normal with mean and standard deviation

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
45
The daily revenue at a university snack bar has been recorded for the past five years. Records indicate that the mean daily revenue is $1500 and the standard deviation is $500. The distribution is skewed to the right due to several high volume days (football game days). Suppose that 100 days are randomly selected and the average daily revenue computed. Which of the following describes the sampling distribution of the sample mean?
A) normally distributed with a mean of $1500 and a standard deviation of $500
B) skewed to the right with a mean of $1500 and a standard deviation of $500
C) normally distributed with a mean of $150 and a standard deviation of $50
D) normally distributed with a mean of $1500 and a standard deviation of $50
A) normally distributed with a mean of $1500 and a standard deviation of $500
B) skewed to the right with a mean of $1500 and a standard deviation of $500
C) normally distributed with a mean of $150 and a standard deviation of $50
D) normally distributed with a mean of $1500 and a standard deviation of $50

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
46
The term statistic refers to a population quantity, and the term parameter refers to a sample quantity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
47
The standard error of the sampling distribution of the sample mean is equal to ?, the standard deviation of the population.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
48
A random sample of n = 300 measurements is drawn from a binomial population with probability of success .43. Give the mean and the standard deviation of the sampling distribution of the sample Proportion,
A) .43; .014
B) 57; .014
C) .43; .029
D) .57; .029
A) .43; .014
B) 57; .014
C) .43; .029
D) .57; .029

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
49

A) .26; .025
B) .26; .011
C) .74; .011
D) .74; .025

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
50
A random sample of n = 400 measurements is drawn from a binomial population with probability of success .21. Give the mean and the standard deviation of the sampling distribution of the sample Proportion,
A) .79; .008
B) .21; .008
C) .79; .02
D) .21; .02
A) .79; .008
B) .21; .008
C) .79; .02
D) .21; .02

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
51
The Central Limit Theorem is important in statistics because _____.
A) for a large n, it says the sampling distribution of the sample mean is approximately normal, regardless of the population
B) for any population, it says the sampling distribution of the sample mean is approximately normal, regardless of the sample size
C) for a large n, it says the population is approximately normal
D) for any size sample, it says the sampling distribution of the sample mean is approximately normal
A) for a large n, it says the sampling distribution of the sample mean is approximately normal, regardless of the population
B) for any population, it says the sampling distribution of the sample mean is approximately normal, regardless of the sample size
C) for a large n, it says the population is approximately normal
D) for any size sample, it says the sampling distribution of the sample mean is approximately normal

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck
52
The minimum-variance unbiased estimator (MVUE) has the least variance among all unbiased estimators.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 52 في هذه المجموعة.
فتح الحزمة
k this deck








