Deck 5: Exponential and Logarithmic Functions and Equations
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/186
العب
ملء الشاشة (f)
Deck 5: Exponential and Logarithmic Functions and Equations
1
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
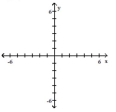
A) domain: ; range:
horizontal asymptote:
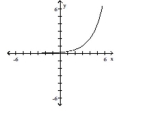
B) domain: ; range:
horizontal asymptote:
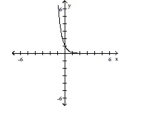
C) domain: ; range:
horizontal asymptote:
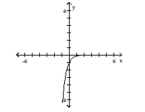
D) domain: ; range:
horizontal asymptote:
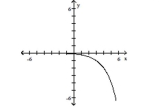

A) domain: ; range:
horizontal asymptote:

B) domain: ; range:
horizontal asymptote:

C) domain: ; range:
horizontal asymptote:

D) domain: ; range:
horizontal asymptote:

A
2
Use transformations to graph the function.
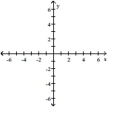
A)
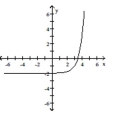
B)
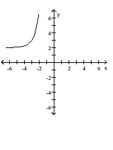
C)
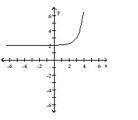
D)
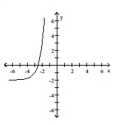

A)

B)

C)

D)

A
3
Use transformations to graph the function.
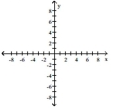
A)
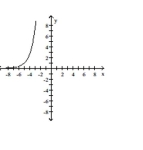
B)
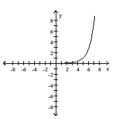
C)
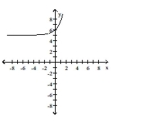
D)
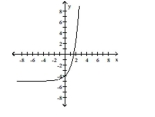

A)

B)

C)

D)

C
4
Approximate the value using a calculator. Round your answer to three decimal places.
A)0.633
B)-2.990
C)-0.333
D)0.333
A)0.633
B)-2.990
C)-0.333
D)0.333

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
5
Convert the equation to the standard form for a hyperbola by completing the square.
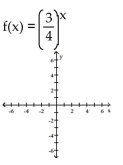 A)
A)
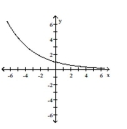
B)
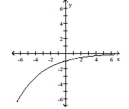
C)
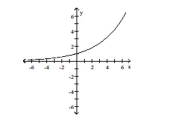
D)
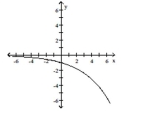
 A)
A)
B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
6
Approximate the value using a calculator. Round your answer to three decimal places.
A)25.672
B)27.113
C)8.970
D)15.154
A)25.672
B)27.113
C)8.970
D)15.154

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
7
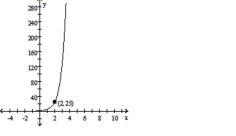
Convert the equation to the standard form for a hyperbola by completing the square.
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
8
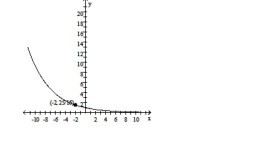
Convert the equation to the standard form for a hyperbola by completing the square.
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
9
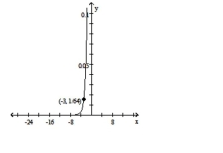
Convert the equation to the standard form for a hyperbola by completing the square.
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
10
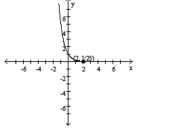
Convert the equation to the standard form for a hyperbola by completing the square.
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
11
Convert the equation to the standard form for a hyperbola by completing the square.
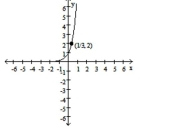
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
12
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
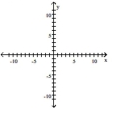
A) domain: ; range:
horizontal asymptote:
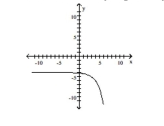
B) domain: ; range:
horizontal asymptote:
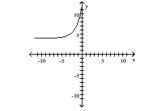
C) domain: ; range:
horizontal asymptote:
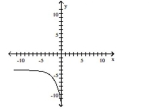
D) domain: ; range:
horizontal asymptote:
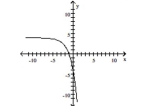

A) domain: ; range:
horizontal asymptote:

B) domain: ; range:
horizontal asymptote:

C) domain: ; range:
horizontal asymptote:

D) domain: ; range:
horizontal asymptote:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
13
Convert the equation to the standard form for a hyperbola by completing the square.
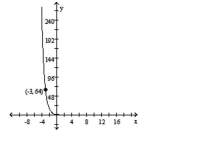
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
14
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
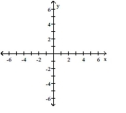
A) domain: ; range:
horizontal asymptote:
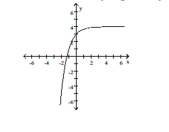
B) domain: ; range:
horizontal asymptote:
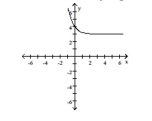
C) domain: ; range:
horizontal asymptote:
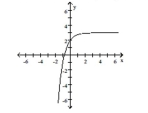
D) domain: ; range:
horizontal asymptote:
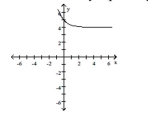

A) domain: ; range:
horizontal asymptote:

B) domain: ; range:
horizontal asymptote:

C) domain: ; range:
horizontal asymptote:

D) domain: ; range:
horizontal asymptote:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
15
Graph the function.
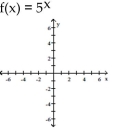 A)
A)
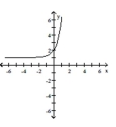
B)
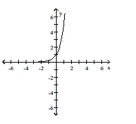
C)
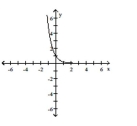
D)
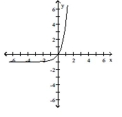
 A)
A)
B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
16
Convert the equation to the standard form for a hyperbola by completing the square.
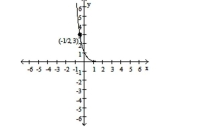
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
17
Use transformations to graph the function.
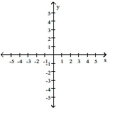
A)
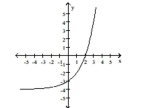
B)
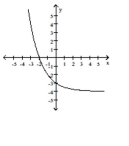
C)
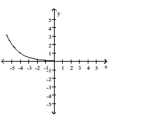
D)
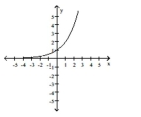

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
18
Graph the function.
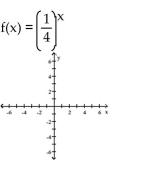 A)
A)
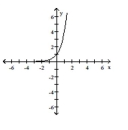
B)
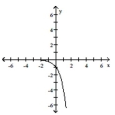
C)
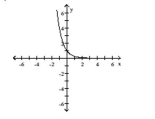
D)
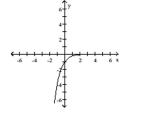
 A)
A)
B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
19
Approximate the value using a calculator. Round your answer to three decimal places.
A)23.141
B)22.459
C)8.540
D)5.860
A)23.141
B)22.459
C)8.540
D)5.860

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
20
Use transformations to graph the function.
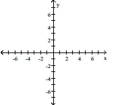
A)
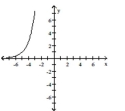
B)
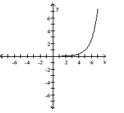
C)
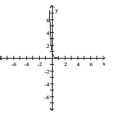
D)
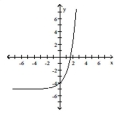

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
21
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
22
Solve the problem.
Laura borrows $5000 at a rate of 9% compounded monthly. Find how much Laura owes at the end of 4 years. Use: where:
final amount
(the amount borrowed)
(the annual rate of interest)
(the number of times interest is compounded each year)
(the duration of the loan in years)
A)$241,800.00
B)$7157.03
C)$7872.73
D)$5151.70
Laura borrows $5000 at a rate of 9% compounded monthly. Find how much Laura owes at the end of 4 years. Use: where:
final amount
(the amount borrowed)
(the annual rate of interest)
(the number of times interest is compounded each year)
(the duration of the loan in years)
A)$241,800.00
B)$7157.03
C)$7872.73
D)$5151.70

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
23
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
24
Solve the problem.
The formula gives the average atmospheric pressure, , in pounds per square inch, at an altitude , in miles above sea level. Find the average atmospheric pressure for an altitude of miles. Round your answer to the nearest tenth.
A) in.
B)
C)
D) in.
The formula gives the average atmospheric pressure, , in pounds per square inch, at an altitude , in miles above sea level. Find the average atmospheric pressure for an altitude of miles. Round your answer to the nearest tenth.
A) in.
B)
C)
D) in.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
25
Solve the problem.
Find the amount in a savings account at the end of 4 years if the amount originally deposited is $9000 and the interest rate is 5.5% compounded monthly. Use: where:
final amount
(the initial deposit)
(the annual rate of interest)
(the number of times interest is compounded each year)
(the duration of the deposit in vears)
A)$433,980.00
B)$12,329.96
C)$9166.14
D)$11,209.06
Find the amount in a savings account at the end of 4 years if the amount originally deposited is $9000 and the interest rate is 5.5% compounded monthly. Use: where:
final amount
(the initial deposit)
(the annual rate of interest)
(the number of times interest is compounded each year)
(the duration of the deposit in vears)
A)$433,980.00
B)$12,329.96
C)$9166.14
D)$11,209.06

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
26
Solve the problem.
The function D(h)= 8e-0.4h can be used to determine the milligrams D of a certain drug in a patient's bloodstream h hours after the drug has been given. How many milligrams (to two decimals)will be present after 12 hours?
A)4.76 mg
B)0.07 mg
C)972.08 mg
D)0.49 mg
The function D(h)= 8e-0.4h can be used to determine the milligrams D of a certain drug in a patient's bloodstream h hours after the drug has been given. How many milligrams (to two decimals)will be present after 12 hours?
A)4.76 mg
B)0.07 mg
C)972.08 mg
D)0.49 mg

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
27
Solve the problem.
The rabbit population in a forest area grows at the rate of 7% monthly. If there are 270 rabbits in September, find how many rabbits (rounded to the nearest whole number)should be expected by next September. Use
A)609
B)612
C)622
D)635
The rabbit population in a forest area grows at the rate of 7% monthly. If there are 270 rabbits in September, find how many rabbits (rounded to the nearest whole number)should be expected by next September. Use
A)609
B)612
C)622
D)635

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
28
Solve the problem.
Four bacteria are placed in a petri dish. The population will triple every day. The formula for the number of bacteria in the dish on day t , where t is the number of days after the four bacteria are placed in the dish. How many bacteria are in the dish six days after the four bacteria are placed in the dish?
A)864
B)72
C)13
D)2916
Four bacteria are placed in a petri dish. The population will triple every day. The formula for the number of bacteria in the dish on day t , where t is the number of days after the four bacteria are placed in the dish. How many bacteria are in the dish six days after the four bacteria are placed in the dish?
A)864
B)72
C)13
D)2916

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
29
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
30
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
31
Solve the problem.
A city is growing at the rate of 0.9% annually. If there were 5,400,000 residents in the city in 1992, find how many (to the nearest ten-thousand)were living in that city in 2000.
A)14,580,000
B)5,800,000
C)5,830,000
D)1,050,000
A city is growing at the rate of 0.9% annually. If there were 5,400,000 residents in the city in 1992, find how many (to the nearest ten-thousand)were living in that city in 2000.
A)14,580,000
B)5,800,000
C)5,830,000
D)1,050,000

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
32
Determine the correct exponential function of the form f(x)= bx whose graph is given.
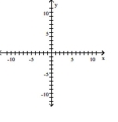
A)
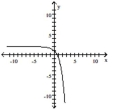
B)
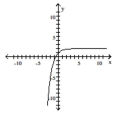
C)
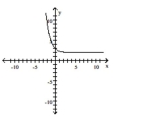
D)
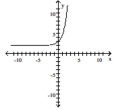

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
33
Solve the problem.
The amount of a radioactive substance present, in grams, at time t in months is given by the formula y = 8000(2)-0.3t. Find the number of grams present in 2 years. If necessary, round to three decimal places.
A)527.803
B)5278.032
C)54.409
D)5.441
The amount of a radioactive substance present, in grams, at time t in months is given by the formula y = 8000(2)-0.3t. Find the number of grams present in 2 years. If necessary, round to three decimal places.
A)527.803
B)5278.032
C)54.409
D)5.441

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
34
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
35
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
36
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
37
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
В)
C)
D)
A)
В)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
38
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
39
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
40
Determine the correct exponential function of the form f(x)= bx whose graph is given.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
41
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
42
Solve the equation.
Which has a lower present value: $30,000 if interest is paid at a rate of 5.98% compounded continuously for 5 years, or $33,000 if interest is paid at a rate of 3.3% compounded continuously for 65 months?
A)$33,000 with interest is paid at a rate of 3.3% compounded continuously for 65 months has a lower present value.
B)$30,000 with interest paid at a rate of 5.98% compounded continuously for 5 years has a lower present value.
C)Both investments have the same present value.
Which has a lower present value: $30,000 if interest is paid at a rate of 5.98% compounded continuously for 5 years, or $33,000 if interest is paid at a rate of 3.3% compounded continuously for 65 months?
A)$33,000 with interest is paid at a rate of 3.3% compounded continuously for 65 months has a lower present value.
B)$30,000 with interest paid at a rate of 5.98% compounded continuously for 5 years has a lower present value.
C)Both investments have the same present value.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
43
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
44
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
45
Solve the problem.
Instruments on a satellite measure the amount of power generated by the satellite's power supply. The time t and the power P can be modeled by the funct , where t is in days and P is in watts. How much power will be available after 378 days? Round to the nearest hundredth.
A)14.32 watts
B)4.11 watts
C)14.18 watts
D)15.95 watts
Instruments on a satellite measure the amount of power generated by the satellite's power supply. The time t and the power P can be modeled by the funct , where t is in days and P is in watts. How much power will be available after 378 days? Round to the nearest hundredth.
A)14.32 watts
B)4.11 watts
C)14.18 watts
D)15.95 watts

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
46
Write the logarithmic equation as an exponential equation.
A)-3
B)81
C)3
D)-81
A)-3
B)81
C)3
D)-81

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
47
Write the exponential equation as an equation involving a logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
48
Write the logarithmic equation as an exponential equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
49
Solve the problem.
An initial investment of $1740 is appreciated for 14 years in an account that earns 7% interest, compounded continuously. Find the amount of money in the account at the end of the period. Round to the nearest cent.
A)$6,127,559.21
B)$12,856.96
C)$4636.15
D)$2868.78
An initial investment of $1740 is appreciated for 14 years in an account that earns 7% interest, compounded continuously. Find the amount of money in the account at the end of the period. Round to the nearest cent.
A)$6,127,559.21
B)$12,856.96
C)$4636.15
D)$2868.78

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
50
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
51
Solve the problem.
Suppose your great-great grandmother invested $700 earning 3.6% interest compounded continuously 120 years ago. How much would her investment be worth today? Round to the nearest cent.
A)$52,632.04
B)$52,620.80
C)$818.18
D)$52,620.83
Suppose your great-great grandmother invested $700 earning 3.6% interest compounded continuously 120 years ago. How much would her investment be worth today? Round to the nearest cent.
A)$52,632.04
B)$52,620.80
C)$818.18
D)$52,620.83

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
52
Write the logarithmic equation as an exponential equation.
A)8
B)16
C)4
D)2
A)8
B)16
C)4
D)2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
53
Solve the problem.
An original investment of $7000 earns 7% interest compounded continuously. What will the investment be worth in 3 years? Round to the nearest cent.
A)$8470.00
B)$8635.75
C)$8735.75
D)$8575.30
An original investment of $7000 earns 7% interest compounded continuously. What will the investment be worth in 3 years? Round to the nearest cent.
A)$8470.00
B)$8635.75
C)$8735.75
D)$8575.30

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
54
Solve the problem.
A rumor is spread at an elementary school with 1200 students according to the model where N is the number of students who have heard the rumor and d is the number of days that have elapsed since the rumor began. How many students will have heard the rumor after 5 days?
A)1063 students
B)1006 students
C)661 students
D)689 students
A rumor is spread at an elementary school with 1200 students according to the model where N is the number of students who have heard the rumor and d is the number of days that have elapsed since the rumor began. How many students will have heard the rumor after 5 days?
A)1063 students
B)1006 students
C)661 students
D)689 students

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
55
Write the exponential equation as an equation involving a logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
56
Solve the problem.
Suppose that you have $12,000 to invest. Which investment yields the greater return over 7 years: 8.75% compounded continuously or 8.9% compounded semiannually?
A)$12,000 invested at 8.9% compounded semiannually over 7 years yields the greater return.
B)$12,000 invested at 8.75% compounded continuously over 7 years yields the greater return.
C)Both investment plans yield the same return.
Suppose that you have $12,000 to invest. Which investment yields the greater return over 7 years: 8.75% compounded continuously or 8.9% compounded semiannually?
A)$12,000 invested at 8.9% compounded semiannually over 7 years yields the greater return.
B)$12,000 invested at 8.75% compounded continuously over 7 years yields the greater return.
C)Both investment plans yield the same return.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
57
Write the exponential equation as an equation involving a logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
58
Write the logarithmic equation as an exponential equation.
A)9
B)-2
C)2
D)-9
A)9
B)-2
C)2
D)-9

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
59
Write the exponential equation as an equation involving a logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
60
Solve the problem.
Suppose that $6000 is invested at an interest rate of 5.2% per year, compounded continuously. What is the balance after 2 years?Round to the nearest cent.
A)$6312.00
B)$6757.60
C)$6657.60
D)$6624.00
Suppose that $6000 is invested at an interest rate of 5.2% per year, compounded continuously. What is the balance after 2 years?Round to the nearest cent.
A)$6312.00
B)$6757.60
C)$6657.60
D)$6624.00

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
61
Write the logarithmic equation as an exponential equation.
ln
A) 2
B)
C) 4
D) e
ln
A) 2
B)
C) 4
D) e

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
62
Write the exponential equation as an equation involving a common logarithm or a natural logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
63
Write the logarithmic equation as an exponential equation.
A)
B) 40
C)
D) 4
A)
B) 40
C)
D) 4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
64
Write the exponential equation as an equation involving a common logarithm or a natural logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
65
Write the logarithmic equation as an exponential equation.
A)e
B)10
C)1
A)e
B)10
C)1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
66
Write the logarithmic equation as an exponential equation.
ln l
A)-1
B)1
C)0
D)e
ln l
A)-1
B)1
C)0
D)e

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
67
Write the logarithmic equation as an exponential equation.
ln e
A)0
B)1
C)-1
D)e
ln e
A)0
B)1
C)-1
D)e

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
68
Write the exponential equation as an equation involving a common logarithm or a natural logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
69
Write the logarithmic equation as an exponential equation.
A) 7
B)
C) 8
D)
A) 7
B)
C) 8
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
70
Write the logarithmic equation as an exponential equation.
A)
B)
C)
D) 4
A)
B)
C)
D) 4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
71
Evaluate the logarithm without the use of a calculator.
A)1
B)3
C)-12
D)-4
A)1
B)3
C)-12
D)-4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
72
Use the properties of logarithms to evaluate the expression without the use of a calculator.
A)1
B)6
C)4
D)24
A)1
B)6
C)4
D)24

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
73
Use the properties of logarithms to evaluate the expression without the use of a calculator.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
74
Write the logarithmic equation as an exponential equation.
A)1
C)0
D)3
A)1
C)0
D)3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
75
Evaluate the logarithm without the use of a calculator.
A) 7
B)
C)
D) 1
A) 7
B)
C)
D) 1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
76
Write the logarithmic equation as an exponential equation.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
77
Write the exponential equation as an equation involving a common logarithm or a natural logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
78
Use the properties of logarithms to evaluate the expression without the use of a calculator.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
79
Write the exponential equation as an equation involving a common logarithm or a natural logarithm.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck
80
Use the properties of logarithms to evaluate the expression without the use of a calculator.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 186 في هذه المجموعة.
فتح الحزمة
k this deck








