Deck 6: Conic Sections
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/97
العب
ملء الشاشة (f)
Deck 6: Conic Sections
1
Find the vertex, focus, and directrix of the parabola with the given equation.
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
D
2
Find the vertex, focus, and directrix of the parabola with the given equation.
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
A
3
Graph the equation.
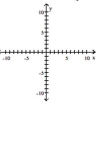
A)
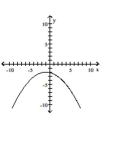
B)
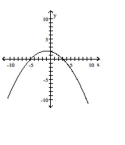
C)
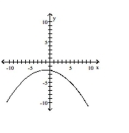
D)
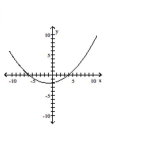

A)

B)

C)

D)

A
4
Find the vertex, focus, and directrix of the parabola. Graph the equation.
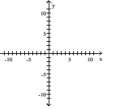
A) vertex:
focus:
directrix:
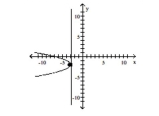
B) vertex:
focus:
directrix:
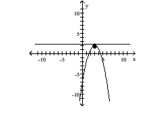
C) vertex:
focus:
directrix:
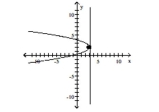
D) vertex:
focus:
directrix:
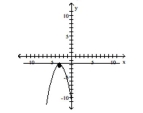

A) vertex:
focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
5
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
A)
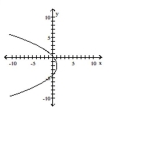
B)
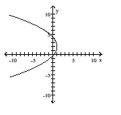
C)
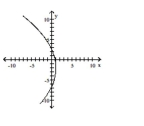
D)
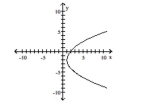

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the vertex, focus, and directrix of the parabola with the given equation.
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
7
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The vertex has coordinates (0, 0), and the focus has coordinates (6, 0). A)
B)
C)
D)
The vertex has coordinates (0, 0), and the focus has coordinates (6, 0). A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
8
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The vertex has coordinates (6, 9), and the focus has coordinates (7, 9). A)
B)
C)
D)
The vertex has coordinates (6, 9), and the focus has coordinates (7, 9). A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
9
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The focus has coordinates (-15, 0), and the equation of the directrix is x = 15. A)
B)
C)
D)
The focus has coordinates (-15, 0), and the equation of the directrix is x = 15. A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find the vertex, focus, and directrix of the parabola with the given equation.
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
A) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
11
Graph the equation.
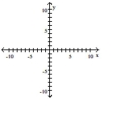
A)
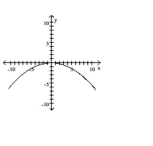
B)
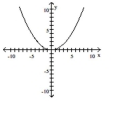
C)
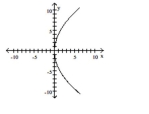
D)
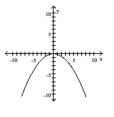

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
12
Find the vertex, focus, and directrix of the parabola. Graph the equation.
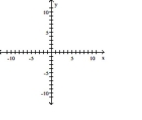
A)
vertex:
focus:
directrix:
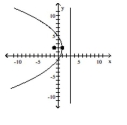
B) vertex:
focus:
directrix:
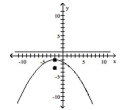
C) vertex:
focus:
directrix:
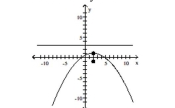
D) vertex:
focus:
directrix:
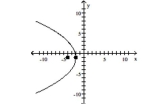

A)
vertex:
focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
13
Graph the equation.
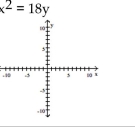 A)
A)
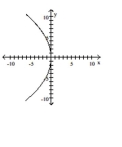
B)
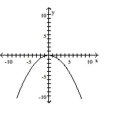
C)
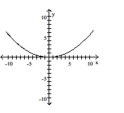
D)
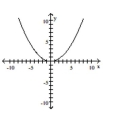
 A)
A)
B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
14
Graph the equation.
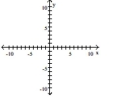
A)
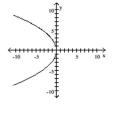
B)
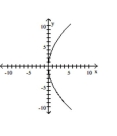
C)
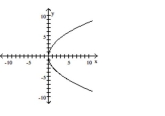
D)
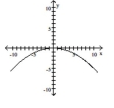

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
15
Graph the equation.
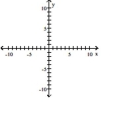
A)
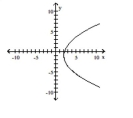
B)
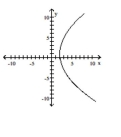
C)
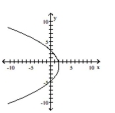
D)
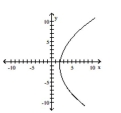

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
16
Graph the equation.
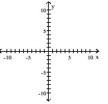
A)
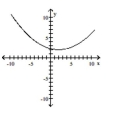
B)
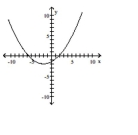
C)
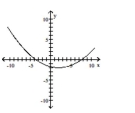
D)
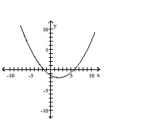

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
17
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The focus has coordinates (0, 19), and the equation of the directrix is y = -19. A)
B)
C)
D)
The focus has coordinates (0, 19), and the equation of the directrix is y = -19. A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
18
Find the vertex, focus, and directrix of the parabola. Graph the equation.
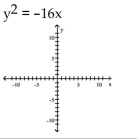 A) vertex:
A) vertex:
focus:
directrix:
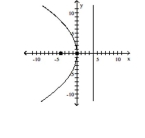
B) vertex:
focus:
directrix:
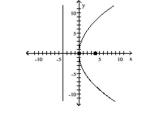
C) vertex:
focus:
directrix:
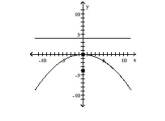
D) vertex:
focus:
directrix:
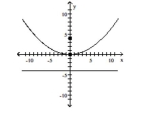
 A) vertex:
A) vertex: focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
19
Graph the equation.
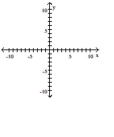
A)
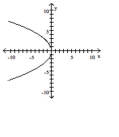
B)
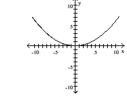
C)
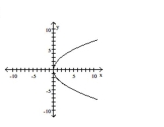
D)
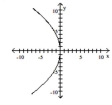

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find the vertex, focus, and directrix of the parabola. Graph the equation.
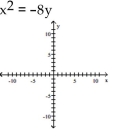 A) vertex:
A) vertex:
focus:
directrix:
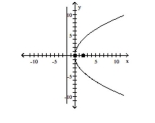
B) vertex:
focus:
directrix:
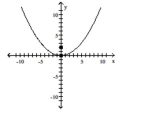

 A) vertex:
A) vertex: focus:
directrix:

B) vertex:
focus:
directrix:



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
21
Graph the ellipse and locate the foci.
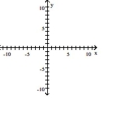
A) foci at and
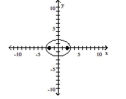
B) foci at and
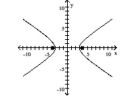
C) foci at and
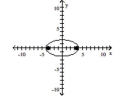
D) foci at and
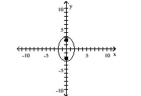

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
22
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The vertex has coordinates (5, 6), and the focus has coordinates (5, 3). A)
B)
C)
D)
The vertex has coordinates (5, 6), and the focus has coordinates (5, 3). A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
23
Find the center, foci, and vertices of the ellipse.
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
24
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The vertex has coordinates (9, -3), and the focus has coordinates (9, -7). A)
B)
C)
D)
The vertex has coordinates (9, -3), and the focus has coordinates (9, -7). A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
25
Solve the problem.
A reflecting telescope contains a parabolic mirror. If the mirror is 24 inches across at its opening and is 4 feet deep, where will the light be concentrated?
A)0.3 in. from the vertex
B)0.8 in. from the vertex
C)0.7 in. from the vertex
D)9 in. from the vertex
A reflecting telescope contains a parabolic mirror. If the mirror is 24 inches across at its opening and is 4 feet deep, where will the light be concentrated?
A)0.3 in. from the vertex
B)0.8 in. from the vertex
C)0.7 in. from the vertex
D)9 in. from the vertex

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the center, foci, and vertices of the ellipse.
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
27
Graph the equation.
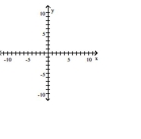
A)
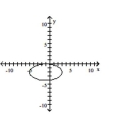
B)
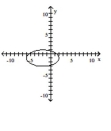
C)
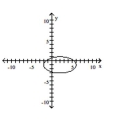
D)
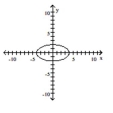

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
28
Solve the problem.
A searchlight is shaped like a parabola. If the light source is located 3 feet from the base along the axis of symmetry and the opening is 8 feet across, how deep should the searchlight be?
A)0.6 ft
B)1.3 ft
C)5.3 ft
D)4 ft
A searchlight is shaped like a parabola. If the light source is located 3 feet from the base along the axis of symmetry and the opening is 8 feet across, how deep should the searchlight be?
A)0.6 ft
B)1.3 ft
C)5.3 ft
D)4 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
29
Graph the ellipse and locate the foci.
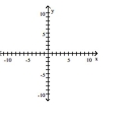
A) foci at and
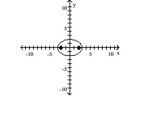
B) foci at and
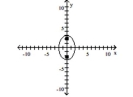
C) foci at and
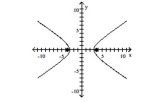
D) foci at and
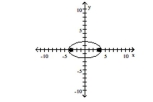

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the center, foci, and vertices of the ellipse.
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
31
Find the center, foci, and vertices of the ellipse.
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at and
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
32
Find the vertex, focus, and directrix of the parabola. Graph the equation.
A) vertex:
focus:
directrix:
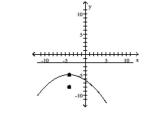
B) vertex:
focus:
directrix:
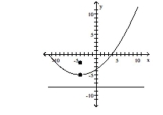
C) vertex:
focus:
directrix:
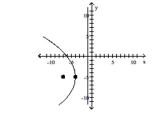
D) vertex:
focus:
directrix:
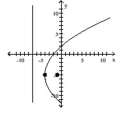

A) vertex:
focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
33
Determine if each ordered pair is a solution to the given system of inequalities in two variables.
The vertex has coordinates (3, -5), and the focus has coordinates (4, -5). A)
B)
C)
D)
The vertex has coordinates (3, -5), and the focus has coordinates (4, -5). A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
34
Graph the ellipse and locate the foci.
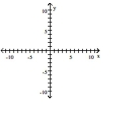
A) foci at and
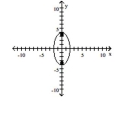
B) foci at and
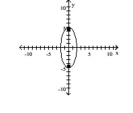
C) foci at and
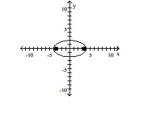
D) foci at and

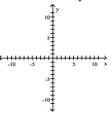
A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find the center, foci, and vertices of the ellipse.
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at
A) center at
foci at and
vertices at
B) center at
foci at and
vertices at
C) center at
foci at and
vertices at
D) center at
foci at and
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
36
Find the vertex, focus, and directrix of the parabola. Graph the equation.
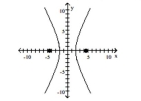
A) vertex:
focus:
directrix:
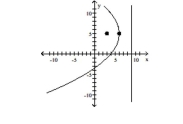
B) vertex:
focus:
directrix:
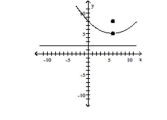


A) vertex:
focus:
directrix:

B) vertex:
focus:
directrix:



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find the center, foci, and vertices of the ellipse.
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
38
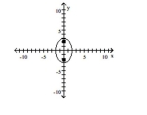
Graph the equation.
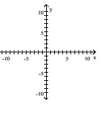
A)
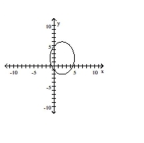
B)
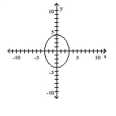
C)
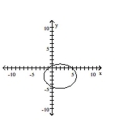
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
39
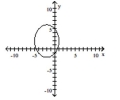
Graph the ellipse and locate the foci.

A) foci at and
B) foci at and
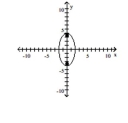
C) foci at and
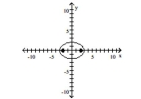
D) foci at and
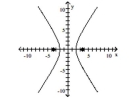

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
40
Solve the problem.
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 160 feet and a maximum height of 40 feet. Find the height of the arch at 10 feet from its center.
A)2.5 ft
B)39.4 ft
C)0.2 ft
D)5 ft
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 160 feet and a maximum height of 40 feet. Find the height of the arch at 10 feet from its center.
A)2.5 ft
B)39.4 ft
C)0.2 ft
D)5 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find an equation for the ellipse described.
Foci at (1, 4)and (-5, 4); vertex at (-8, 4) A)
B)
C)
D)
Foci at (1, 4)and (-5, 4); vertex at (-8, 4) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find an equation for the ellipse described.
Foci at (1, 4)and (7, 4); length of major axis is 10 A)
В)
C)
D)
Foci at (1, 4)and (7, 4); length of major axis is 10 A)
В)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find an equation for the ellipse described.
Focus at (-2, 0); vertices at (-8, 0)and (8, 0) A)
B)
C)
D)
Focus at (-2, 0); vertices at (-8, 0)and (8, 0) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
44
Find the equation in standard form of the parabola described.
Center at (-4, 5); focus at (-6, 5); contains the point (-9, 5) A)
B)
D)
Center at (-4, 5); focus at (-6, 5); contains the point (-9, 5) A)
B)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find an equation for the ellipse described.
Vertices at (5, -4)and (5, 8); length of minor axis is 6 A)
B)
C)
D)
Vertices at (5, -4)and (5, 8); length of minor axis is 6 A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find the equation in standard form of the parabola described.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find an equation for the ellipse described.
Center at (0, 0); focus at (-2, 0); vertex at (3, 0) A)
B)
C)
D)
Center at (0, 0); focus at (-2, 0); vertex at (3, 0) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find an equation for the ellipse described.
Foci at (-3, 4)and (-3, -2); length of major axis is 10 A)
B)
C)
D)
Foci at (-3, 4)and (-3, -2); length of major axis is 10 A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find an equation for the ellipse described.
Foci at (0, -3)and (0, 3); length of the major axis is 12 A)
B)
C)
D)
Foci at (0, -3)and (0, 3); length of the major axis is 12 A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find an equation for the ellipse described.
Center at (3, 3); focus at (9, 3); vertex at (11, 3) A)
B)
C)
D)
Center at (3, 3); focus at (9, 3); vertex at (11, 3) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
51
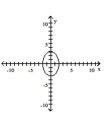
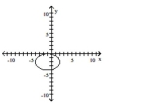
Graph the equation.
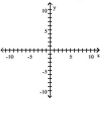
A)
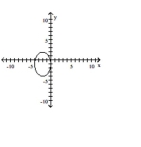
B)
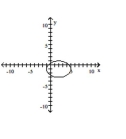
C)
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
52
Write an equation for the graph.
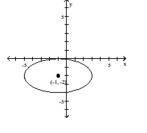
A)
B)
C)
D)

A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
53
Find an equation for the ellipse described.
Focus at (0, -6); vertices at (0, -7)and (0, 7) A)
B)
C)
D)
Focus at (0, -6); vertices at (0, -7)and (0, 7) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
54
Find an equation for the ellipse described.
Center at (0, 0); focus at (0, -5); vertex at (0, 8) A)
B)
C)
D)
Center at (0, 0); focus at (0, -5); vertex at (0, 8) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
55
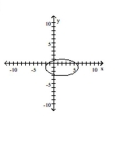
Graph the equation.
A)
B)
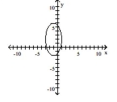
C)
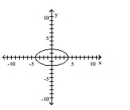
D)
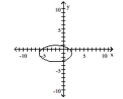

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find an equation for the ellipse described.
Center (0, 0); major axis horizontal with length 8; length of minor axis is 4 A)
B)
C)
D)
Center (0, 0); major axis horizontal with length 8; length of minor axis is 4 A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
57
Find an equation for the ellipse described.
Center at (0, 0); focus at (-5, 0); vertex at (8, 0) A)
B)
C)
D)
Center at (0, 0); focus at (-5, 0); vertex at (8, 0) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
58
Find an equation for the ellipse described.
Vertices at (-6, 2)and (14, 2); focus at (12, 2) A)
B)
C)
D)
Vertices at (-6, 2)and (14, 2); focus at (12, 2) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find an equation for the ellipse described.
Center at (0, 0); focus at (5, 0); vertex at (8, 0) A)
B)
C)
D)
Center at (0, 0); focus at (5, 0); vertex at (8, 0) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
60
Find an equation for the ellipse described.
Center (0, 0); major axis vertical with length 12; length of minor axis is 8 A)
В)
C)
D)
Center (0, 0); major axis vertical with length 12; length of minor axis is 8 A)
В)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
B) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
C) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
D) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
A) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
B) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
C) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
D) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
62
Graph the hyperbola.
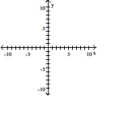
A)
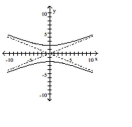
B)
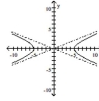
C)
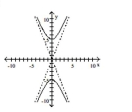
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
63
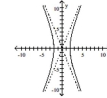
Graph the hyperbola.
A)
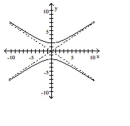
B)
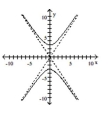
C)
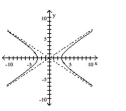
D)
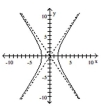

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
64
Graph the hyperbola.
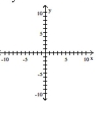
A)
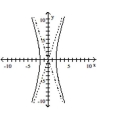
B)
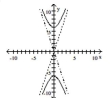
C)
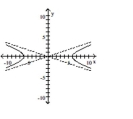
D)
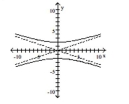

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
65
Find the center, transverse axis, vertices, and foci of the hyperbola.
A) center at
transverse axis is -axis
vertices:
foci:
B) center at
transverse axis is -axis
vertices:
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices:
foci:
A) center at
transverse axis is -axis
vertices:
foci:
B) center at
transverse axis is -axis
vertices:
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices:
foci:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find the equation in standard form of the parabola described.
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
67
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
B) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
C) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
D) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
A) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
B) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
C) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
D) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
68
Graph the hyperbola.
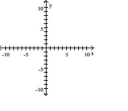
A)
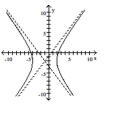
B)
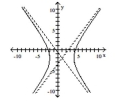
C)
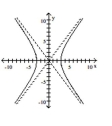
D)
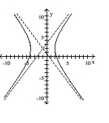

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
69
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
B) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
C) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
D) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
A) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
B) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
C) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
D) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
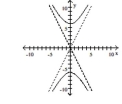
70
Graph the hyperbola.
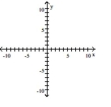
A)
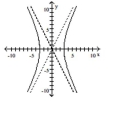
B)
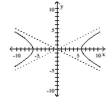
C)
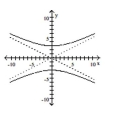
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
71
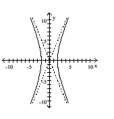
Graph the hyperbola.
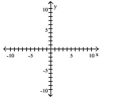
A)
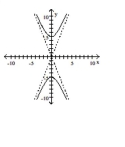
B)
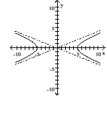
C)
D)
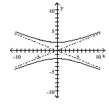

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center at
transverse axis is parallel to -axis
vertices at and ,
foci at and ,
asymptotes of and
B) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
C) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
D) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
A) center at
transverse axis is parallel to -axis
vertices at and ,
foci at and ,
asymptotes of and
B) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
C) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and
D) center at
transverse axis is parallel to -axis
vertices at and
foci at and
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
73
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center:
transverse axis is parallel to -axis
vertices: and ;
foci: and
asymptotes of and
B) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
C) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
D) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
A) center:
transverse axis is parallel to -axis
vertices: and ;
foci: and
asymptotes of and
B) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
C) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and
D) center:
transverse axis is parallel to -axis
vertices: and
foci: and
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
74
Graph the hyperbola.
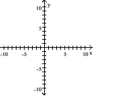
A)
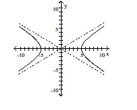
B)
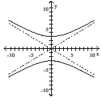
C)
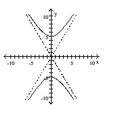
D)
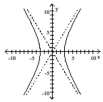

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find the center, transverse axis, vertices, and foci of the hyperbola.
A) center at
transverse axis is -axis
vertices:
foci:
B) center at
transverse axis is -axis
vertices:
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices at and
foci at and
A) center at
transverse axis is -axis
vertices:
foci:
B) center at
transverse axis is -axis
vertices:
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices at and
foci at and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
76
Find the center, transverse axis, vertices, foci, and asymptotes of the hyperbola.
A) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
B) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
C) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
D) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
A) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
B) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
C) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and
D) center at
transverse axis is -axis
vertices:
foci:
asymptotes of and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
77
Solve the problem.
An arch for a bridge over a highway is in the form of a semiellipse. The top of the arch is 35 feet above ground (the major axis). What should the span of the bridge be (the length of its minor axis)if the height 27 feet from the center is to be 16 feet above ground?
A)60.72 ft
B)30.36 ft
C)50.29 ft
D)118.13 ft
An arch for a bridge over a highway is in the form of a semiellipse. The top of the arch is 35 feet above ground (the major axis). What should the span of the bridge be (the length of its minor axis)if the height 27 feet from the center is to be 16 feet above ground?
A)60.72 ft
B)30.36 ft
C)50.29 ft
D)118.13 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
78
Find the center, transverse axis, vertices, and foci of the hyperbola.
A) center at
transverse axis is -axis
vertices:
oci:
B) center at
transverse axis is -axis
vertices: f
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices:
foci:
A) center at
transverse axis is -axis
vertices:
oci:
B) center at
transverse axis is -axis
vertices: f
foci:
C) center at
transverse axis is -axis
vertices:
foci:
D) center at
transverse axis is -axis
vertices:
foci:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
79
Solve the problem.
A bridge is built in the shape of a semielliptical arch. It has a span of 102 feet. The height of the arch 27 feet from the center is to be 11 feet. Find the height of the arch at its center.
A)11.41 ft
B)20.78 ft
C)12.97 ft
D)27.65 ft
A bridge is built in the shape of a semielliptical arch. It has a span of 102 feet. The height of the arch 27 feet from the center is to be 11 feet. Find the height of the arch at its center.
A)11.41 ft
B)20.78 ft
C)12.97 ft
D)27.65 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck
80
Find the center, transverse axis, vertices, and foci of the hyperbola.
A) center at
transverse axis is -axis
vertices at and
foci at and
B) center at
transverse axis is -axis
vertices at and
foci at and
C) center at
transverse axis is -axis
vertices at and
foci at and
D) center at
transverse axis is -axis
vertices at and
foci at and
A) center at
transverse axis is -axis
vertices at and
foci at and
B) center at
transverse axis is -axis
vertices at and
foci at and
C) center at
transverse axis is -axis
vertices at and
foci at and
D) center at
transverse axis is -axis
vertices at and
foci at and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 97 في هذه المجموعة.
فتح الحزمة
k this deck








