Deck 5: Sequences, Mathematical Induction, and Recursion
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/37
العب
ملء الشاشة (f)
Deck 5: Sequences, Mathematical Induction, and Recursion
1
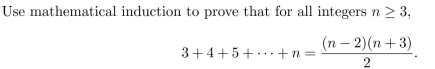


2
Transform the following summation by making the change of variable i = k + 1: 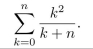
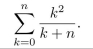
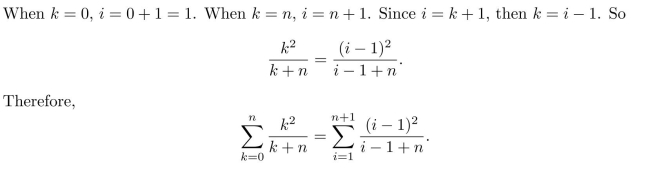
3



4
Use mathematical induction to prove that for all integers 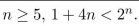
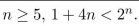

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
5
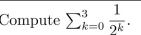

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
6
Use mathematical induction to prove that for all integers 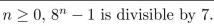
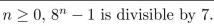

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
7
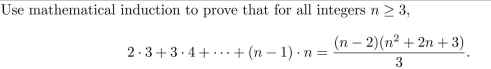

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
8
Use the formula 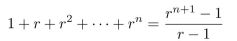
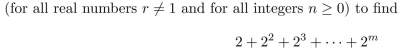
where m is an integer that is at least 1.
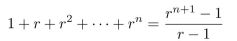
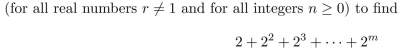
where m is an integer that is at least 1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
9



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
10
Use strong mathematical induction to prove that for all integers 
either n is prime or n
is a product of prime numbers.

either n is prime or n
is a product of prime numbers.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
11
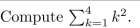

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
12

(a) Is P(0) true? Justify your answer.

(c) Finish the proof started in (b) above.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
13
Use summation notation to rewrite the following: 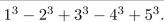
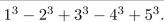

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
14
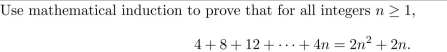

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
15
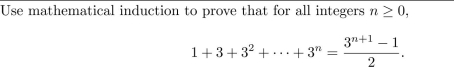

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
16
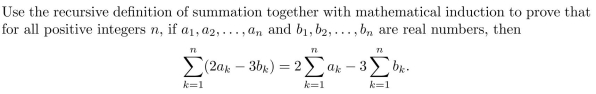

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
17
Use a summation symbol to rewrite the following: 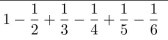
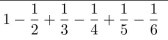

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
18
Use repeated division by 2 to find the binary representation of the number 1032. Show your
work.
work.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
19
Transform the following summation by making the change of variable j = k + 1 : 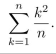
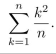

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
20
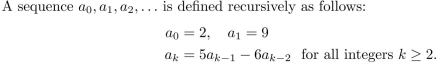
Use strong mathematical induction to prove that for all integers
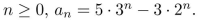

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
21
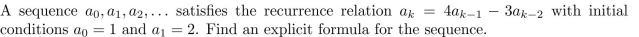

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
22
In a Triple Tower of Hanoi, there are three poles in a row and 3n disks, three of each of n
different sizes, where n is any positive integer. Initially, one of the poles contains all the disks
placed on top of each other in triples of decreasing size. Disks are transferred one by one from
one pole to another, but at no time may a larger disk be placed on top of a smaller disk.
However, a disk may be placed on top of one of the same size. Let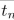
be the minimum number
of moves needed to transfer a tower of 3n disks from one pole to another. Find a recurrence
relation for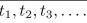
Justify your answer carefully.
different sizes, where n is any positive integer. Initially, one of the poles contains all the disks
placed on top of each other in triples of decreasing size. Disks are transferred one by one from
one pole to another, but at no time may a larger disk be placed on top of a smaller disk.
However, a disk may be placed on top of one of the same size. Let
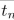
be the minimum number
of moves needed to transfer a tower of 3n disks from one pole to another. Find a recurrence
relation for
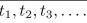
Justify your answer carefully.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
23


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
24


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
25
A sequence is defined recursively as follows: 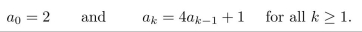
It is proposed that an explicit formula for this sequence is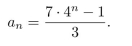
Use mathematical induction to check whether this proposed formula is correct.
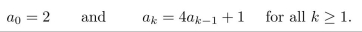
It is proposed that an explicit formula for this sequence is
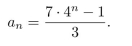
Use mathematical induction to check whether this proposed formula is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
26


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
27
A sequence 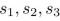
... is defined recursively as follows: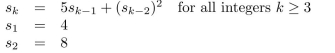
Use (strong) mathematical induction to prove that sn is divisible by 4 for all integers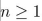
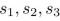
... is defined recursively as follows:
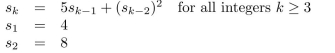
Use (strong) mathematical induction to prove that sn is divisible by 4 for all integers
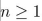

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
28

If appropriate, simplify your answer using one of the following reference formulas:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
29
The following while loop is annotated with a pre- and post-condition and also a loop invariant.
Use the loop invariant theorem to prove the correctness of the loop with respect to the pre-
and post-conditions.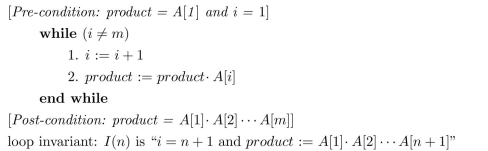
Use the loop invariant theorem to prove the correctness of the loop with respect to the pre-
and post-conditions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
30


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
31


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
32


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
33
In a Double Tower of Hanoi with Adjacency Requirement there are three poles in a row and
2n disks, two of each of n different sizes, where n is any positive integer. Initially pole A (at
one end of the row) contains all the disks, placed on top of each other in pairs of decreasing
size. Disks may only be transferred one-by-one from one pole to an adjacent pole and at no
time may a larger disk be placed on top of a smaller one. However a disk may be placed on
top of another one of the same size. Let C be the pole at the other end of the row and let

2n disks, two of each of n different sizes, where n is any positive integer. Initially pole A (at
one end of the row) contains all the disks, placed on top of each other in pairs of decreasing
size. Disks may only be transferred one-by-one from one pole to an adjacent pole and at no
time may a larger disk be placed on top of a smaller one. However a disk may be placed on
top of another one of the same size. Let C be the pole at the other end of the row and let



فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
34

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
35


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
36
A sequence is defined recursively as follows: 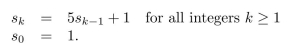
Use mathematical induction to verify that this sequence satisfies the explicit formula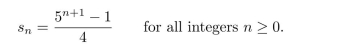
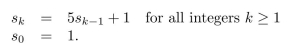
Use mathematical induction to verify that this sequence satisfies the explicit formula
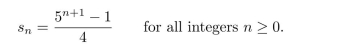

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck
37

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 37 في هذه المجموعة.
فتح الحزمة
k this deck








