Deck 5: Conics
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/63
العب
ملء الشاشة (f)
Deck 5: Conics
1
Match the equation to the graph.
A)
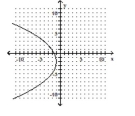
B)
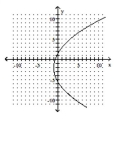
C)
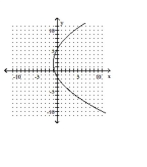
D)
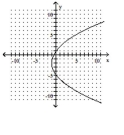
A)

B)

C)

D)

D
2
Name the conic.
A)
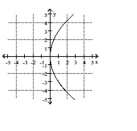
B)
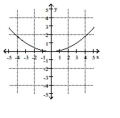
C)
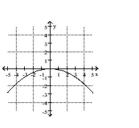
D)
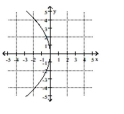
A)

B)

C)

D)

B
3
Name the conic.
A)
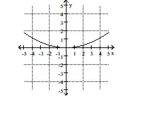
B)
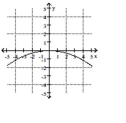
C)
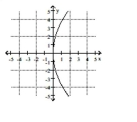
D)
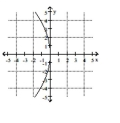
A)

B)

C)

D)

B
4
Write an equation for the parabola.
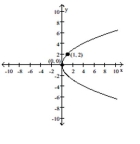
A) y2 = 4x
B) y2 = -4x
C) x2 = -4y
D) x2 = 4y

A) y2 = 4x
B) y2 = -4x
C) x2 = -4y
D) x2 = 4y

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
5
Name the conic.
Vertex at (0, 0); axis of symmetry the x-axis; containing the point (8, 6) A)
B)
C)
D)
Vertex at (0, 0); axis of symmetry the x-axis; containing the point (8, 6) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
6
Match the equation to the graph.
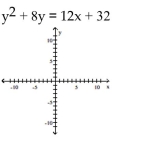 A) vertex:
A) vertex:
focus:
directrix:
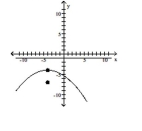
B) vertex:
focus:
directrix:
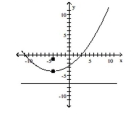
C) vertex:
focus:
directrix:
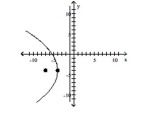
D) vertex:
focus:
directrix:
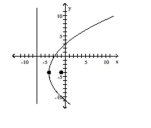
 A) vertex:
A) vertex: focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
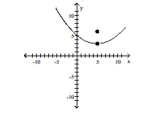
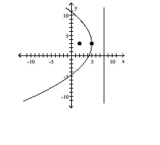
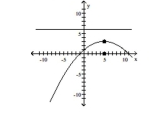
7
Match the equation to the graph.
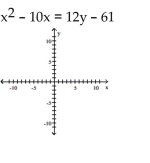 A) vertex:
A) vertex:
focus:
directrix:
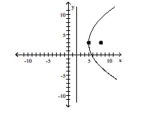
B) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
 A) vertex:
A) vertex: focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
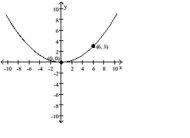
8
Write an equation for the parabola.
 A)
A)
В)
C)
D)
 A)
A) В)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
9
Graph the equation.
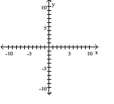
A)
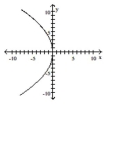
B)
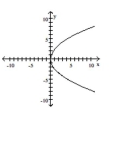
C)
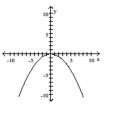
D)
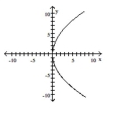

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
10
Match the equation to the graph.
A)
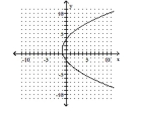
B)
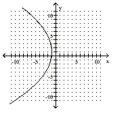
C)
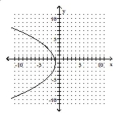
D)
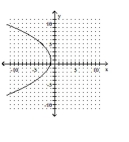
A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
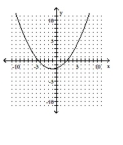
11
Match the equation to the graph.
A)
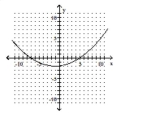
B)
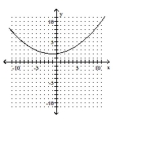
C)
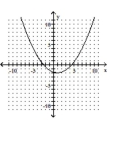
D)
A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
12
Find the vertex, focus, and directrix of the parabola.
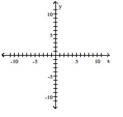
 C) vertex:
C) vertex:
focus:
directrix:
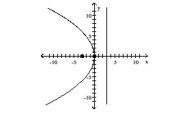
D) vertex:
focus:
directrix:
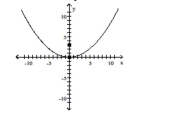

 C) vertex:
C) vertex: focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find the vertex, focus, and directrix of the parabola.
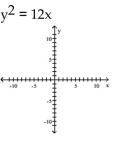 A) vertex:
A) vertex:
focus:
directrix:
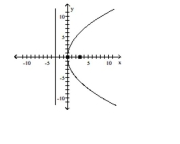
B) vertex:
focus:
directrix:
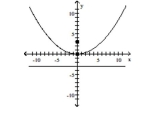 C) vertex:
C) vertex:
focus:
directrix:
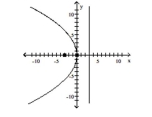
D) vertex:
focus:
directrix:
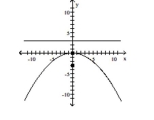
 A) vertex:
A) vertex: focus:
directrix:

B) vertex:
focus:
directrix:
 C) vertex:
C) vertex: focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
14
Name the conic.
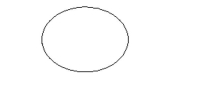
A) hyperbola
B) ellipse
C) circle
D) parabola

A) hyperbola
B) ellipse
C) circle
D) parabola

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
15
Name the conic.
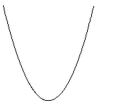
A) parabola
B) ellipse
C) circle
D) hyperbola

A) parabola
B) ellipse
C) circle
D) hyperbola

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
16
Match the equation to the graph.
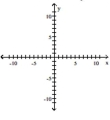
A) vertex:
focus:
directrix:
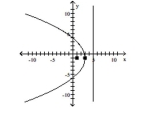
B) vertex:
focus:
directrix:
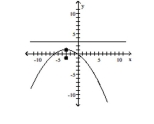
C) vertex:
focus:
directrix:
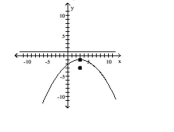
D) vertex:
focus:
directrix:
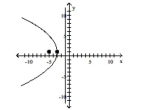

A) vertex:
focus:
directrix:

B) vertex:
focus:
directrix:

C) vertex:
focus:
directrix:

D) vertex:
focus:
directrix:


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
17
Graph the equation.
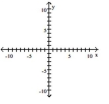
A)
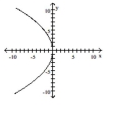
B)
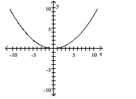
C)
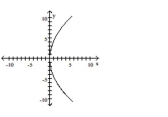
D)
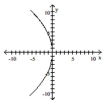

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
18
Name the conic.
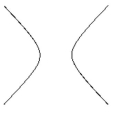
A) ellipse
B) parabola
C) hyperbola
D) circle

A) ellipse
B) parabola
C) hyperbola
D) circle

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
19
Name the conic.
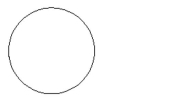
A) parabola
B) ellipse
C) hyperbola
D) circle

A) parabola
B) ellipse
C) hyperbola
D) circle

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find an equation of the parabola described and state the two points that define the latus rectum.
Focus at (0, 1); directrix the line y = -1
A) x2 = 4y; latus rectum: (2, 1) and (-2, 1)
B) x2 = 8y; latus rectum: (4, 1) and (-4, 1)
C) x2 = 4y; latus rectum: (1, 2) and (-1, 2)
D) y2 = 8x; latus rectum: (3, 4) and (-3, 4)
Focus at (0, 1); directrix the line y = -1
A) x2 = 4y; latus rectum: (2, 1) and (-2, 1)
B) x2 = 8y; latus rectum: (4, 1) and (-4, 1)
C) x2 = 4y; latus rectum: (1, 2) and (-1, 2)
D) y2 = 8x; latus rectum: (3, 4) and (-3, 4)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
21
Graph the equation.
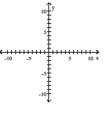
A)
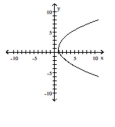
B)
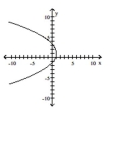
C)
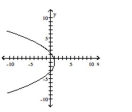
D)
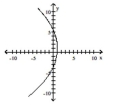

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
22
Graph the equation.
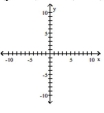
A)
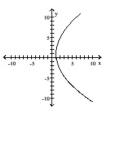
B)
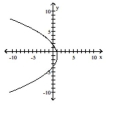
C)
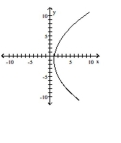
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
23
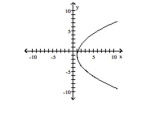
Graph the equation.
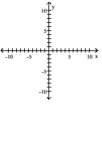
A)
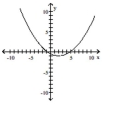
B)
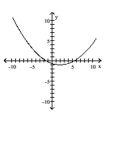
C)
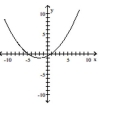
D)
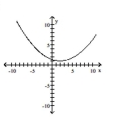

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
24
Graph the ellipse and locate the foci.
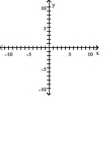
A) foci at and
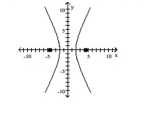
B) foci at and
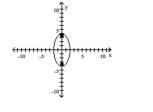
C) foci at and
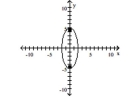
D) foci at and
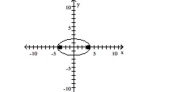

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
25
Graph the ellipse and locate the foci.
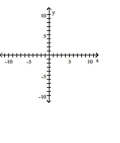
A) foci at and
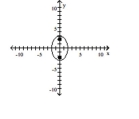
B) foci at and
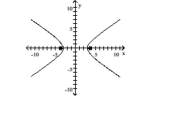
C) foci at and
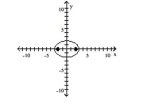
D) foci at and
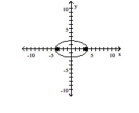

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the center, foci, and vertices of the ellipse.
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
27
Solve the problem.
A satellite dish is shaped like a paraboloid of revolution. The signals that emanate from a satellite strike the
surface of the dish and are reflected to a single point, where the receiver is located. If the dish is 8 feet across at
its opening and is 2 feet deep at its center, at what position should the receiver be placed?
A satellite dish is shaped like a paraboloid of revolution. The signals that emanate from a satellite strike the
surface of the dish and are reflected to a single point, where the receiver is located. If the dish is 8 feet across at
its opening and is 2 feet deep at its center, at what position should the receiver be placed?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
28
Solve the problem.
A searchlight is shaped like a paraboloid of revolution. If the light source is located 5 feet from the base along the axis of symmetry and the opening is 14 feet across, how deep should the searchlight be?
A) 12.3 ft
B) 2.5 ft
C) 9.8 ft
D) 0.9 ft
A searchlight is shaped like a paraboloid of revolution. If the light source is located 5 feet from the base along the axis of symmetry and the opening is 14 feet across, how deep should the searchlight be?
A) 12.3 ft
B) 2.5 ft
C) 9.8 ft
D) 0.9 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
29
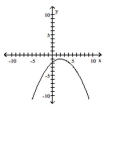
Graph the equation.
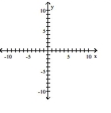
A)
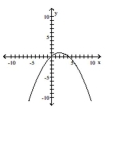
B)
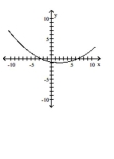
C)
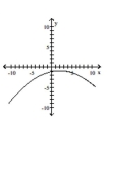
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
30
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers stand 60 inches apart. At a point between the towers and 18 inches along the road from the
Base of one tower, the cable is 1.44 inches above the roadway. Find the height of the towers.
A) 11 in.
B) 9 in.
C) 8.5 in.
D) 9.5 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers stand 60 inches apart. At a point between the towers and 18 inches along the road from the
Base of one tower, the cable is 1.44 inches above the roadway. Find the height of the towers.
A) 11 in.
B) 9 in.
C) 8.5 in.
D) 9.5 in.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
31
Solve the problem.
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 142 feet and a maximum height of 25 feet. Find the height of the arch at 25 feet from its center.
A) 21.9 ft
B) 0.8 ft
C) 71 ft
D) 12.4 ft
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 142 feet and a maximum height of 25 feet. Find the height of the arch at 25 feet from its center.
A) 21.9 ft
B) 0.8 ft
C) 71 ft
D) 12.4 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
32
Solve the problem.
A spotlight has a parabolic cross section that is 6 ft wide at the opening and 2.5 ft deep at the vertex. How far from the vertex is the focus? Round answer to two decimal places.
A) 0.90 ft
B) 0.21 ft
C) 0.52 ft
D) 0.26 ft
A spotlight has a parabolic cross section that is 6 ft wide at the opening and 2.5 ft deep at the vertex. How far from the vertex is the focus? Round answer to two decimal places.
A) 0.90 ft
B) 0.21 ft
C) 0.52 ft
D) 0.26 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
33
Solve the problem.
A reflecting telescope contains a mirror shaped like a paraboloid of revolution. If the mirror is 20 inches across at its opening and is 5 feet deep, where will the light be concentrated?
A) 5 in. from the vertex
B) 1.3 in. from the vertex
C) 0.6 in. from the vertex
D) 0.4 in. from the vertex
A reflecting telescope contains a mirror shaped like a paraboloid of revolution. If the mirror is 20 inches across at its opening and is 5 feet deep, where will the light be concentrated?
A) 5 in. from the vertex
B) 1.3 in. from the vertex
C) 0.6 in. from the vertex
D) 0.4 in. from the vertex

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
34
Write an equation for the graph.
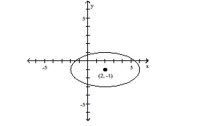 A)
A)
B)
C)
D)
 A)
A) B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
35
Solve the problem.
A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is
3 centimeters from the vertex. If the depth is to be 6 centimeters, what is the diameter of the headlight at its
opening?
A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is
3 centimeters from the vertex. If the depth is to be 6 centimeters, what is the diameter of the headlight at its
opening?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
36
Graph the ellipse and locate the foci.
A) foci at and
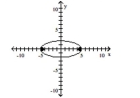
B) foci at and
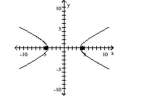
C) foci at and
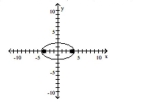
D) foci at and
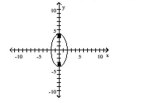
A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
37
Solve the problem.
A reflecting telescope has a mirror shaped like a paraboloid of revolution. If the distance of the vertex to the focus is 30 feet and the distance across the top of the mirror is 50 inches, how deep is the mirror in the center? A) 9 in.
B) .
C) in.
D)
A reflecting telescope has a mirror shaped like a paraboloid of revolution. If the distance of the vertex to the focus is 30 feet and the distance across the top of the mirror is 50 inches, how deep is the mirror in the center? A) 9 in.
B) .
C) in.
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
38
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. Find the vertical distance from the
Roadway to the cable at a point on the road 14 inches from the lowest point of the cable.
A) 1.76 in.
B) 7.84 in.
C) 2.16 in.
D) 1.96 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. Find the vertical distance from the
Roadway to the cable at a point on the road 14 inches from the lowest point of the cable.
A) 1.76 in.
B) 7.84 in.
C) 2.16 in.
D) 1.96 in.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
39
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 9 inches tall and stand 60 inches apart. At some point along the road from the lowest
Point of the cable, the cable is 0.81 inches above the roadway. Find the distance between that point and the base
Of the nearest tower.
A) 21.2 in.
B) 9.2 in.
C) 21 in.
D) 8.8 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 9 inches tall and stand 60 inches apart. At some point along the road from the lowest
Point of the cable, the cable is 0.81 inches above the roadway. Find the distance between that point and the base
Of the nearest tower.
A) 21.2 in.
B) 9.2 in.
C) 21 in.
D) 8.8 in.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
40
Graph the ellipse and locate the foci.
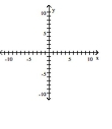
A) foci at and
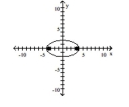
B) foci at and
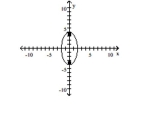
C) foci at and
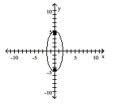
D) foci at and
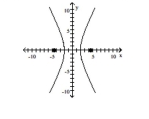

A) foci at and

B) foci at and

C) foci at and

D) foci at and


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find an equation for the ellipse described. Graph the equation.
Foci at (1, 3) and (-5, 3); vertex at (-9, 3)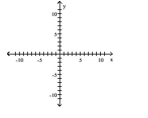
A)
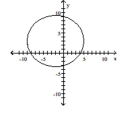
B)
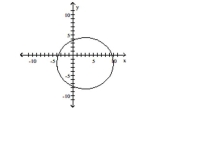
C)
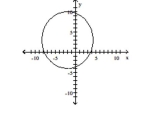
D)
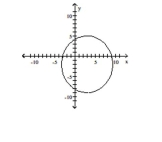
Foci at (1, 3) and (-5, 3); vertex at (-9, 3)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find an equation for the ellipse described. Graph the equation.
Foci at (-1, 7) and (-1, 1); length of major axis is 10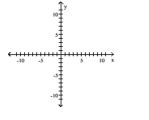
A)
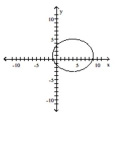
B)
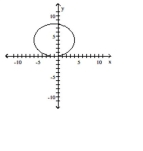
C)
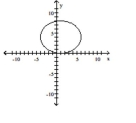
D)
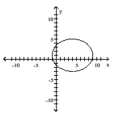
Foci at (-1, 7) and (-1, 1); length of major axis is 10

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the center, foci, and vertices of the ellipse.
A)
center: ; foci: ; vertices:
B)
center: ; foci: ; vertices:
C)
center: ; foci: ; vertices: ,
D)
center: ; foci: ; vertices:
A)
center: ; foci: ; vertices:
B)
center: ; foci: ; vertices:
C)
center: ; foci: ; vertices: ,
D)
center: ; foci: ; vertices:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
44
Find the center, foci, and vertices of the ellipse.
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at
A) center at
foci at
vertices at
B) center at
foci at
vertices at
C) center at
foci at
vertices at
D) center at
foci at
vertices at

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
45
Solve the problem.
An arch for a bridge over a highway is in the form of a semiellipse. The top of the arch is 30 feet above ground (the major axis). What should the span of the bridge be (the length of its minor axis) if the height 29 feet from the
Center is to be 15 feet above ground?
A) 117.17 ft
B) 116 ft
C) 33.49 ft
D) 66.97 ft
An arch for a bridge over a highway is in the form of a semiellipse. The top of the arch is 30 feet above ground (the major axis). What should the span of the bridge be (the length of its minor axis) if the height 29 feet from the
Center is to be 15 feet above ground?
A) 117.17 ft
B) 116 ft
C) 33.49 ft
D) 66.97 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find an equation for the ellipse described. Graph the equation.
Vertices at (5, -4) and (5, 8); length of minor axis is 6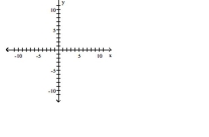
A)
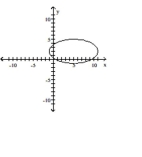
B)
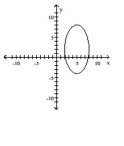
C)
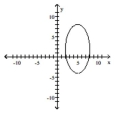
D)
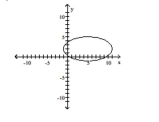
Vertices at (5, -4) and (5, 8); length of minor axis is 6

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find an equation for the ellipse described. Graph the equation.
Center at (-2, 4); focus at (-8, 4); contains the point (-10, 4)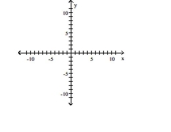
A)
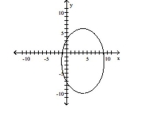
B)
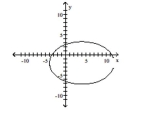
C)
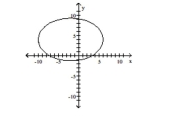
D)
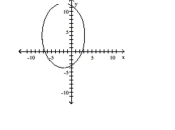
Center at (-2, 4); focus at (-8, 4); contains the point (-10, 4)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find an equation for the ellipse described. Graph the equation.
Foci at (0, 3) and (6, 3); length of major axis is 10
A)
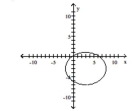
B)
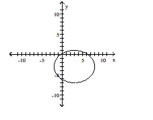
C)
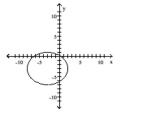
D)
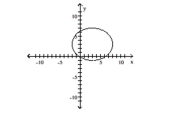
Foci at (0, 3) and (6, 3); length of major axis is 10

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find an equation for the ellipse described.
Center at ; focus at ; vertex at
A)
B)
C)
D)
Center at ; focus at ; vertex at
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
50
Match the equation to the graph.
A)
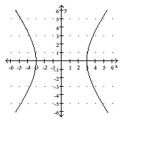
B)
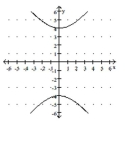
C)
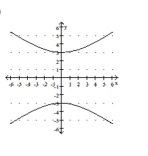
D)
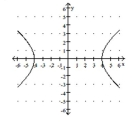
A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
51
Match the equation to the graph.
A)
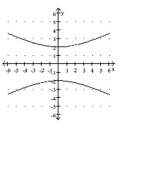
B)
 br>C)
br>C)
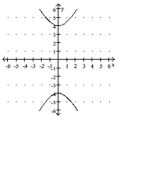
D)
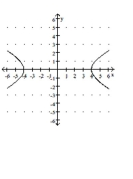
A)

B)
 br>C)
br>C)
D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
52
Find the center, foci, and vertices of the ellipse.
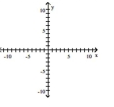
A)
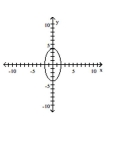
B)
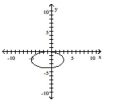
C)
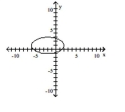
D)
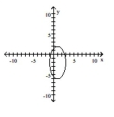

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
53
Solve the problem.
The orbit of a planet around a sun is an ellipse with the sun at one focus. The aphelion of a planet is its greatest distance from the sun, its perihelion is its shortest distance, and its mean distance is the length of the semimajor
Axis of the elliptical orbit. If a planet has a perihelion of 402.3 million miles and a mean distance of 404 million miles, write an equation for the orbit of the planet around the sun. A)
B)
C)
D)
The orbit of a planet around a sun is an ellipse with the sun at one focus. The aphelion of a planet is its greatest distance from the sun, its perihelion is its shortest distance, and its mean distance is the length of the semimajor
Axis of the elliptical orbit. If a planet has a perihelion of 402.3 million miles and a mean distance of 404 million miles, write an equation for the orbit of the planet around the sun. A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
54
Solve the problem.
A race track is in the shape of an ellipse 80 feet long and 60 feet wide. What is the width 32 feet from the center?
A race track is in the shape of an ellipse 80 feet long and 60 feet wide. What is the width 32 feet from the center?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
55
Solve the problem.
An arch in the form of a semiellipse is 52 ft wide at the base and has a height of 20 ft. How wide is the arch at a height of 12 ft above the base?
A) 41.6 ft
B) 17.7 ft
C) 35.5 ft
D) 20.8 ft
An arch in the form of a semiellipse is 52 ft wide at the base and has a height of 20 ft. How wide is the arch at a height of 12 ft above the base?
A) 41.6 ft
B) 17.7 ft
C) 35.5 ft
D) 20.8 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the center, foci, and vertices of the ellipse.
A)
center: ; foci: ; vertices:
B)
center: ; foci: ; vertices:
C)
center: ; foci: ; vertices:
D)
center: ; foci: ; vertices:
A)
center: ; foci: ; vertices:
B)
center: ; foci: ; vertices:
C)
center: ; foci: ; vertices:
D)
center: ; foci: ; vertices:

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
57
Find an equation for the ellipse described.
Vertices at (-2, 4) and (12, 4); focus at (10, 4) A)
B)
C)
D)
Vertices at (-2, 4) and (12, 4); focus at (10, 4) A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
58
Solve the problem.
A bridge is built in the shape of a semielliptical arch. It has a span of 102 feet. The height of the arch 25 feet from the center is to be 11 feet. Find the height of the arch at its center.
A) 25.6 ft
B) 22.44 ft
C) 12.62 ft
D) 11.35 ft
A bridge is built in the shape of a semielliptical arch. It has a span of 102 feet. The height of the arch 25 feet from the center is to be 11 feet. Find the height of the arch at its center.
A) 25.6 ft
B) 22.44 ft
C) 12.62 ft
D) 11.35 ft

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
59
Match the equation to the graph.
A)
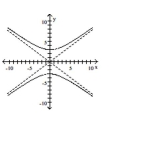
B)
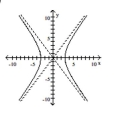
C)
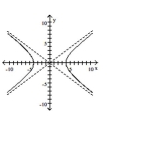
D)
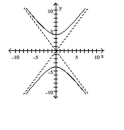
A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
60
Solve the problem.
A hall 130 feet in length was designed as a whispering gallery. If the ceiling is 25 feet high at the center, how far
from the center are the foci located?
A hall 130 feet in length was designed as a whispering gallery. If the ceiling is 25 feet high at the center, how far
from the center are the foci located?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find the asymptotes of the hyperbola.
A satellite following the hyperbolic path shown in the picture turns rapidly at (0, 4) and then moves closer and closer to the line y = 125 x as it gets farther from the tracking station at the origin. Find the equation that
Describes the path of the rocket if the center of the hyperbola is at (0, 0).
(0, 4)
Y = 125 x A)
B)
C)
D)
A satellite following the hyperbolic path shown in the picture turns rapidly at (0, 4) and then moves closer and closer to the line y = 125 x as it gets farther from the tracking station at the origin. Find the equation that
Describes the path of the rocket if the center of the hyperbola is at (0, 0).
(0, 4)
Y = 125 x A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
62
Find the asymptotes of the hyperbola.
A) and
B) and
C) and
D) and
A) and
B) and
C) and
D) and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
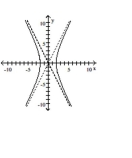
63
Match the equation to the graph.
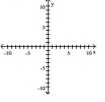
A)
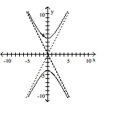
B)
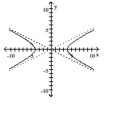
C)
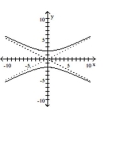
D)

A)

B)

C)

D)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck








