Deck 10: Analytical Geometry
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/8
العب
ملء الشاشة (f)
Deck 10: Analytical Geometry
1
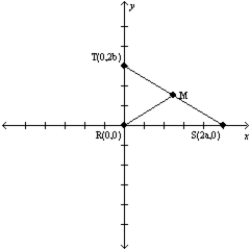
Let a and b represent positive real numbers. Use the right triangle
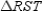 with vertices at R(0,0), S(2a,0), and T(0,2b) to prove the following theorem.
with vertices at R(0,0), S(2a,0), and T(0,2b) to prove the following theorem."The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices of the
triangle."
With  being horizontal and
being horizontal and  being vertical, the right angle is at vertex R. Where M is the midpoint of the hypotenuse
being vertical, the right angle is at vertex R. Where M is the midpoint of the hypotenuse  , we have
, we have 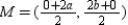 so that
so that 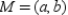 Applying the Distance Formula, we see that the distances from M to the vertices are
Applying the Distance Formula, we see that the distances from M to the vertices are 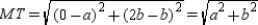 ,
, 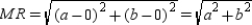 ,
,
and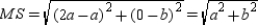 . That is,
. That is, 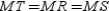 and it follows that midpoint
and it follows that midpoint 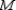 of hypotenuse
of hypotenuse  is equidistant from vertices R, S, and T.
is equidistant from vertices R, S, and T.
 being horizontal and
being horizontal and  being vertical, the right angle is at vertex R. Where M is the midpoint of the hypotenuse
being vertical, the right angle is at vertex R. Where M is the midpoint of the hypotenuse  , we have
, we have 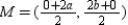 so that
so that 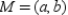 Applying the Distance Formula, we see that the distances from M to the vertices are
Applying the Distance Formula, we see that the distances from M to the vertices are 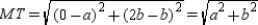 ,
, 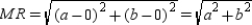 ,
,and
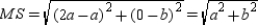 . That is,
. That is, 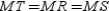 and it follows that midpoint
and it follows that midpoint 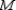 of hypotenuse
of hypotenuse  is equidistant from vertices R, S, and T.
is equidistant from vertices R, S, and T. 2
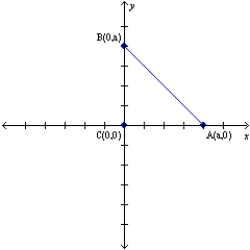
Let a and b represent positive real numbers. Explain why the triangle with vertices at A(a,0), B(0,a) and C(0,0) is an isosceles right triangle.
For  , we apply the Slope Formula to show that
, we apply the Slope Formula to show that 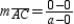 or 0; thus,
or 0; thus, 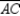 is horizontal. Also,
is horizontal. Also,  , which is undefined; thus,
, which is undefined; thus,  is vertical. Then
is vertical. Then  ,
,
so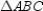 is a right triangle.
is a right triangle.
Because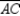 is horizontal, its length is the positive difference is x coordinates; that is,
is horizontal, its length is the positive difference is x coordinates; that is, 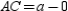 or a. Because
or a. Because 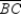 is vertical, its length is the positive difference in its y coordinates; that is,
is vertical, its length is the positive difference in its y coordinates; that is, 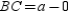 or a. Then
or a. Then 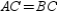 and
and 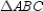 is also isosceles.
is also isosceles.
 , we apply the Slope Formula to show that
, we apply the Slope Formula to show that 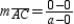 or 0; thus,
or 0; thus, 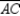 is horizontal. Also,
is horizontal. Also, 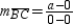 , which is undefined; thus,
, which is undefined; thus,  is vertical. Then
is vertical. Then  ,
,so
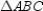 is a right triangle.
is a right triangle.Because
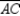 is horizontal, its length is the positive difference is x coordinates; that is,
is horizontal, its length is the positive difference is x coordinates; that is, 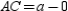 or a. Because
or a. Because 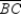 is vertical, its length is the positive difference in its y coordinates; that is,
is vertical, its length is the positive difference in its y coordinates; that is, 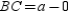 or a. Then
or a. Then 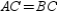 and
and 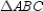 is also isosceles.
is also isosceles. 3

Let a, b, and c represent positive real numbers. Given the rhombus ABCD with vertices at A(0,0), B(a,0), C(a+b,c) and D(b,c), prove the following theorem.
"The diagonals of a rhombus are perpendicular."
With vertices as stated, ABCD appears to be parallelogram. For ABCD to further represent a rhombus, 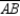 and
and  must be congruent. But
must be congruent. But 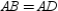 only if
only if 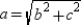 (the result of applying the Distance Formula); in turn,
(the result of applying the Distance Formula); in turn, 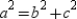 .
.
Having established the conditions for the rhombus, we will now use the Slope Formula to show that the diagonals are perpendicular.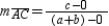 so
so 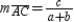 . Similarly,
. Similarly, 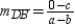 so
so 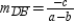 .
.
Then the product of the slopes of these diagonals is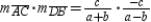 , so
, so 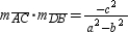 .
.
By substitution (recall that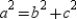 ),
), 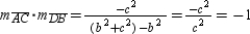 .
.
With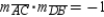 , it follows that
, it follows that 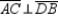 .
.
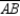 and
and  must be congruent. But
must be congruent. But 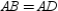 only if
only if 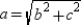 (the result of applying the Distance Formula); in turn,
(the result of applying the Distance Formula); in turn, 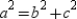 .
.Having established the conditions for the rhombus, we will now use the Slope Formula to show that the diagonals are perpendicular.
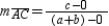 so
so 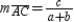 . Similarly,
. Similarly, 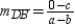 so
so 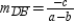 .
.Then the product of the slopes of these diagonals is
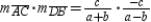 , so
, so 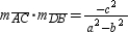 .
.By substitution (recall that
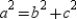 ),
), 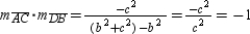 .
.With
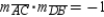 , it follows that
, it follows that 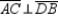 .
. 4
![Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that . [Note: No drawing provided.]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f2_9a91_a05a_658a3066c41e_TB7237_11.jpg)
Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that
![Let a, b, and c represent positive real numbers. Consider the parallelogram ABCD with vertices at A(0,0), B(a,0), C(a+b, c), and D(b,c). In order that ABCD further represents a rhombus, prove that . [Note: No drawing provided.]](https://d2lvgg3v3hfg70.cloudfront.net/TB7237/11eb4b36_76f2_e8bc_a05a_4f86bb001351_TB7237_11.jpg) .
.[Note: No drawing provided.]

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 8 في هذه المجموعة.
فتح الحزمة
k this deck
5
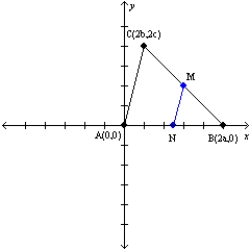
Let a, b, and c represent positive real numbers. Use the drawing in which the vertices of
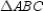 are A(0,0), B(2a,0), and C(2b,2c) to prove the following theorem.
are A(0,0), B(2a,0), and C(2b,2c) to prove the following theorem."The line segment determined by the midpoints of two sides of a triangle is parallel to the third side of the triangle."

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 8 في هذه المجموعة.
فتح الحزمة
k this deck
6
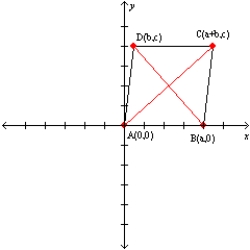
Let a, b, and c represent positive real numbers. Use the figure in which
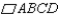 has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem.
has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c) to prove the following theorem."If the diagonals of a parallelogram are equal in length, then the parallelogram is a rectangle."

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 8 في هذه المجموعة.
فتح الحزمة
k this deck
7
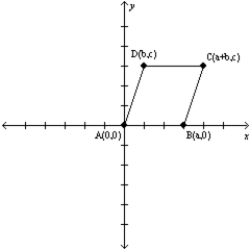
Let a, b, and c represent positive real numbers. Given that quadrilateral ABCD has vertices at A(0,0), B(a,0), C(a+b,c), and D(b,c), explain why ABCD must be a parallelogram.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 8 في هذه المجموعة.
فتح الحزمة
k this deck
8
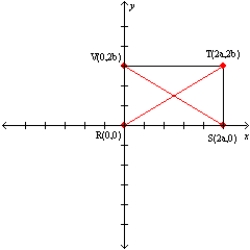
Let a and b represent positive real numbers. Use the drawing in which the vertices of rectangle RSTV are R(0,0), S(2a,0), T(2a,2b), and V(0,2b) to prove the following theorem.
"The diagonals of a rectangle bisect each other."

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 8 في هذه المجموعة.
فتح الحزمة
k this deck








