Deck 5: Game Theory
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/35
العب
ملء الشاشة (f)
Deck 5: Game Theory
1
Consider a simultaneous game in which player A chooses one of two actions (Up or Down), and B chooses one of two actions (Left or Right). The game has the following payoff matrix, where the first payoff in each entry is for A and the second for B. 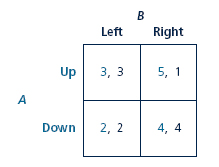
a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?

a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?
In a game of two or more players, each player acts in own interest and try to maximize their payoff. Maximization of the payoff is the only incentive to participate in a game. The game theory builds a model to determine the outcome with the assumption of rational player, uncertainty, and asymmetric information.
The concept of Nash Equilibrium determines the strategies or moves of the players where each strategy is the best response to the other strategy. In a Nash equilibrium strategy, no player has an incentive to deviate from their choices.
Suppose there are two players- player A and player B. Player A play either strategy Up or Down and player B plays either Left or Right.
a.
To compute the Nash equilibrium, fix a strategy for a player and then underline the best response of another player. In the end, with both payoffs underlined is the Nash Equilibrium.
Consider the following game: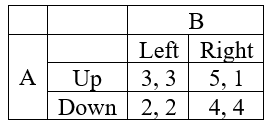 For player A, fix strategy Up. Given the strategy of player A, underline the best response for player B is Left because player B will get more payoff from playing Left (3) rather than Right (1).
For player A, fix strategy Up. Given the strategy of player A, underline the best response for player B is Left because player B will get more payoff from playing Left (3) rather than Right (1).
Again, for player A, fix strategy Down. Given the strategy of player A, underline the best response for player B is Right because player B will get more payoff from playing Right (4) rather than Left (2).
Now, for player B, fix the strategy Left. Given the strategy of player B, underline the best response for player A is Up. This is because player A will get a higher payoff from Up (3) than Down (2).
Now, for player B, fix the strategy Right. Given the strategy of player B, the best response for player A is Up. This is because player A will get a higher payoff from Up (5) than Down (4).
Hence, the Nash equilibrium of the game is (Up, Left).
b. For player A, the dominant strategy is Up. This is because Up strategy returns high payoff against Down strategy (3 and 5 are greater than 2 and 4).
For player B, there is no dominant strategy as no strategy player returns higher payoff.
Hence, player A has a dominant strategy.
The concept of Nash Equilibrium determines the strategies or moves of the players where each strategy is the best response to the other strategy. In a Nash equilibrium strategy, no player has an incentive to deviate from their choices.
Suppose there are two players- player A and player B. Player A play either strategy Up or Down and player B plays either Left or Right.
a.
To compute the Nash equilibrium, fix a strategy for a player and then underline the best response of another player. In the end, with both payoffs underlined is the Nash Equilibrium.
Consider the following game:
 For player A, fix strategy Up. Given the strategy of player A, underline the best response for player B is Left because player B will get more payoff from playing Left (3) rather than Right (1).
For player A, fix strategy Up. Given the strategy of player A, underline the best response for player B is Left because player B will get more payoff from playing Left (3) rather than Right (1). Again, for player A, fix strategy Down. Given the strategy of player A, underline the best response for player B is Right because player B will get more payoff from playing Right (4) rather than Left (2).
Now, for player B, fix the strategy Left. Given the strategy of player B, underline the best response for player A is Up. This is because player A will get a higher payoff from Up (3) than Down (2).
Now, for player B, fix the strategy Right. Given the strategy of player B, the best response for player A is Up. This is because player A will get a higher payoff from Up (5) than Down (4).
Hence, the Nash equilibrium of the game is (Up, Left).
b. For player A, the dominant strategy is Up. This is because Up strategy returns high payoff against Down strategy (3 and 5 are greater than 2 and 4).
For player B, there is no dominant strategy as no strategy player returns higher payoff.
Hence, player A has a dominant strategy.
2
The following game is a version of the Prisoners' Dilemma, but the payoffs are slightly different than in Table 5.1. 
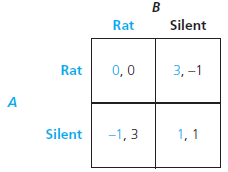
a. Verify that the Nash equilibrium is the usual one for the Prisoners' Dilemma and that both players have dominant strategies.
b. Suppose the stage game is played an indefinite number of times with a probability g the game is continued to the next stage and 1 - g that the game ends for good. Compute the level of g that is required for a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to a grim strategy (that is, both play Rat forever after) if anyone deviates to Rat.
c. Continue to suppose the stage game is played an indefinite number of times, as in b. Is there a value of g for which there exists a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to tit-for-tat (that is, both play Rat for one period and go back to Silent forever after that) if anyone deviates to Rat? Remember that g is a probability, so it must be between 0 and 1.


a. Verify that the Nash equilibrium is the usual one for the Prisoners' Dilemma and that both players have dominant strategies.
b. Suppose the stage game is played an indefinite number of times with a probability g the game is continued to the next stage and 1 - g that the game ends for good. Compute the level of g that is required for a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to a grim strategy (that is, both play Rat forever after) if anyone deviates to Rat.
c. Continue to suppose the stage game is played an indefinite number of times, as in b. Is there a value of g for which there exists a subgame-perfect equilibrium in which both players play a trigger strategy where both are Silent if no one deviates but resort to tit-for-tat (that is, both play Rat for one period and go back to Silent forever after that) if anyone deviates to Rat? Remember that g is a probability, so it must be between 0 and 1.
a) 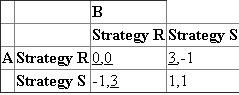 Using the underlining method, Strategy R is the dominant strategy for both the payers. Since, both the players will choose Strategy R in any case; thus, the Nash Equilibrium is (Strategy R, Strategy R).
Using the underlining method, Strategy R is the dominant strategy for both the payers. Since, both the players will choose Strategy R in any case; thus, the Nash Equilibrium is (Strategy R, Strategy R).
b)Expected payoff in equilibrium for the indefinite game is as follows: If a player deviates to strategy R in the first period, his or her payoff is 3 in the first period and 0 from then on.
If a player deviates to strategy R in the first period, his or her payoff is 3 in the first period and 0 from then on.
For the trigger strategies to be an equilibrium,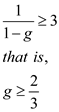 Thus, for equilibrium probability g should be greater than or equal to 2/3.
Thus, for equilibrium probability g should be greater than or equal to 2/3.
c)The expected equilibrium payoff is the same as in part b,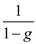 If the player deviates from tit-for-tat, he or she earns 3 in the first period, 0 in the second, and then the players return to the original equilibrium for an expected payoff of,
If the player deviates from tit-for-tat, he or she earns 3 in the first period, 0 in the second, and then the players return to the original equilibrium for an expected payoff of,  For this payoff from deviating to be less than the equilibrium payoff,
For this payoff from deviating to be less than the equilibrium payoff, 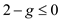 implying
implying 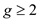 . This is impossible since g is a probability.
. This is impossible since g is a probability.
Thus, players cannot s ustain cooperation on strategy S using tit-for-tat.
 Using the underlining method, Strategy R is the dominant strategy for both the payers. Since, both the players will choose Strategy R in any case; thus, the Nash Equilibrium is (Strategy R, Strategy R).
Using the underlining method, Strategy R is the dominant strategy for both the payers. Since, both the players will choose Strategy R in any case; thus, the Nash Equilibrium is (Strategy R, Strategy R).b)Expected payoff in equilibrium for the indefinite game is as follows:
 If a player deviates to strategy R in the first period, his or her payoff is 3 in the first period and 0 from then on.
If a player deviates to strategy R in the first period, his or her payoff is 3 in the first period and 0 from then on. For the trigger strategies to be an equilibrium,
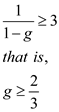 Thus, for equilibrium probability g should be greater than or equal to 2/3.
Thus, for equilibrium probability g should be greater than or equal to 2/3. c)The expected equilibrium payoff is the same as in part b,
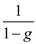 If the player deviates from tit-for-tat, he or she earns 3 in the first period, 0 in the second, and then the players return to the original equilibrium for an expected payoff of,
If the player deviates from tit-for-tat, he or she earns 3 in the first period, 0 in the second, and then the players return to the original equilibrium for an expected payoff of,  For this payoff from deviating to be less than the equilibrium payoff,
For this payoff from deviating to be less than the equilibrium payoff, 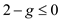 implying
implying 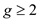 . This is impossible since g is a probability.
. This is impossible since g is a probability. Thus, players cannot s ustain cooperation on strategy S using tit-for-tat.
3
The U.S. government has considered analyzing banking transactions to look for large, suspicious movements of cash as a screen for terrorists. What are the pros and cons of such a screen? How would the terrorists respond in equilibrium if they learned of this screen? Would it still be a useful tool?
Game theory can be used to analyze the money circulation and transfer by terrorists for carrying out the destructive activities. Such money should be detected to foil the expected attacks of destructive nature.
Most important benefit of it is that it will help to track the transfer of suspicion money that may fall in wrong hands. But it is not always successful in meeting its targets. It becomes quite cumbersome to identify the suspicion money.
It is the government strategy to use the screen to identify the illegal and suspicious money. Knowledge of screen would compel the terrorist organization to change their strategies. The loss due to implication in suspicion money transaction may be huge. Hence, the terrorist will definitely switch to other mode of money transfer. It will be Nash equilibrium for them. They are taking the decision only after considering the rival strategies that are committed to thwart the attacks.
In such situation, it will be useful tool to challenge the strategy of terrorists. Terrorist will judge the reliability of this threat, if government has well developed information system and less leakages, it will compel to terrorist organization to look for other strategy.
Most important benefit of it is that it will help to track the transfer of suspicion money that may fall in wrong hands. But it is not always successful in meeting its targets. It becomes quite cumbersome to identify the suspicion money.
It is the government strategy to use the screen to identify the illegal and suspicious money. Knowledge of screen would compel the terrorist organization to change their strategies. The loss due to implication in suspicion money transaction may be huge. Hence, the terrorist will definitely switch to other mode of money transfer. It will be Nash equilibrium for them. They are taking the decision only after considering the rival strategies that are committed to thwart the attacks.
In such situation, it will be useful tool to challenge the strategy of terrorists. Terrorist will judge the reliability of this threat, if government has well developed information system and less leakages, it will compel to terrorist organization to look for other strategy.
4
In game theory, players maximize payoffs. Is this assumption different from the one we used in Chapters 2 and 3?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
5
In the sequential games such as the sequential Battle of the Sexes, why does the Nash equilibrium allow for outcomes with noncredible threats? Why does subgame-perfect equilibrium rule them out?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
6
Is it sensible to model the terrorist as wanting to maximize expected damage? Instead, the terrorist may prefer to attack ''high-visibility'' targets, even if this means lower expected damage, or may prefer to maximize the sum of damage plus defense/deterrence expenditures. Which alternative is most plausible? How would these alternatives affect the game?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
7
In the Battle of the Sexes, does either player have a dominant strategy?
2. In general, can a game have a mixed-strategy Nash equilibrium if a player has a dominant strategy? Why or why not?
2. In general, can a game have a mixed-strategy Nash equilibrium if a player has a dominant strategy? Why or why not?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
8
Find the pure-strategy Nash equilibrium or equilibria of the following game with three actions for each player. 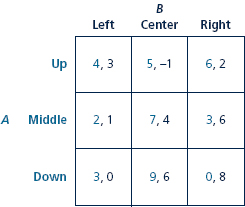


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
9
Suppose A can somehow change the game in problem to a new one in which his payoff from Up is reduced by 2, producing the following payoff matrix. 
a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?
c. Does A benefit from changing the game by reducing his or her payoff in this way?
Consider a simultaneous game in which player A chooses one of two actions (Up or Down), and B chooses one of two actions (Left or Right). The game has the following payoff matrix, where the first payoff in each entry is for A and the second for B.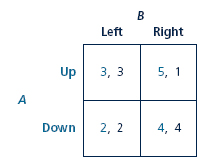
a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?

a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?
c. Does A benefit from changing the game by reducing his or her payoff in this way?
Consider a simultaneous game in which player A chooses one of two actions (Up or Down), and B chooses one of two actions (Left or Right). The game has the following payoff matrix, where the first payoff in each entry is for A and the second for B.

a. Find the Nash equilibrium or equilibria.
b. Which player, if any, has a dominant strategy?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
10
Which of these relationships would be better modeled as involving repetitions and which not, or does it depend? For those that are repeated, which are more realistically seen as involving a definite number of repetitions and which an indefinite number?
a. Two nearby gas stations posting their prices each morning
b. A professor testing students in a course
c. Students entering a dorm room lottery together
d. Accomplices committing a crime
e. Two lions fighting for a mate
a. Two nearby gas stations posting their prices each morning
b. A professor testing students in a course
c. Students entering a dorm room lottery together
d. Accomplices committing a crime
e. Two lions fighting for a mate

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
11
What is the difference between an action and a strategy?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
12
Three department stores, A, B, and C, simultaneously decide whether or not to locate in a mall that is being constructed in town. A store likes to have another with it in the mall since then there is a critical mass of stores to induce shoppers to come out. However, with three stores in the mall, there begins to be too much competition among them and store profits fall drastically. Read the payoff matrix as follows: the first payoff in each entry is for A, the second for B, and the third for C; C's choice determines which of the bold boxes the other players find themselves in. 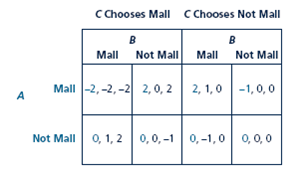
a. Find the pure-strategy Nash equilibrium or equilibria of the game. You can apply the underlying method from the text as follows. First, find the best responses for A and B, treating each bold box corresponding to C's choice as a separate game. Then find C's best responses by comparing corresponding entries in the two boxes (the two entries in the upper-left corners of both, the upper-right corners of both, etc.) and underlining the higher of the two payoffs.
b. What do you think the outcome would be if players chose cooperatively rather than non- cooperatively?

a. Find the pure-strategy Nash equilibrium or equilibria of the game. You can apply the underlying method from the text as follows. First, find the best responses for A and B, treating each bold box corresponding to C's choice as a separate game. Then find C's best responses by comparing corresponding entries in the two boxes (the two entries in the upper-left corners of both, the upper-right corners of both, etc.) and underlining the higher of the two payoffs.
b. What do you think the outcome would be if players chose cooperatively rather than non- cooperatively?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
13
Refer to the normal form of the sequential Battle of the Sexes.
1. Provide examples in which referring to equilibria using payoffs is ambiguous but with strategies is unambiguous.
2. Explain why "Boxing" or "Ballet" is not a complete description of the second mover's strategy.
1. Provide examples in which referring to equilibria using payoffs is ambiguous but with strategies is unambiguous.
2. Explain why "Boxing" or "Ballet" is not a complete description of the second mover's strategy.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
14
In the Tragedy of the Commons, we saw how a small change in A's benefit resulted in a shift in A's best response function and a movement along B's best-response function. Can you think of other factors that might shift A's best-response function? Relate this discussion to shifts in an individual's demand curve versus movements along it.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
15
Return to the game given by the payoff matrix in Problem 5.1.
a. Write down the extensive form for the simultaneousmove game.
b. Suppose the game is now sequential move, with A moving first and then B. Write down the extensive form for this sequential-move game.
c. Write down the normal form for the sequentialmove game. Find all the Nash equilibria. Which Nash equilibrium is subgame-perfect?
a. Write down the extensive form for the simultaneousmove game.
b. Suppose the game is now sequential move, with A moving first and then B. Write down the extensive form for this sequential-move game.
c. Write down the normal form for the sequentialmove game. Find all the Nash equilibria. Which Nash equilibrium is subgame-perfect?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
16
Consider the Tragedy of the Commons game from the chapter with two shepherds, A and B, where s A and s B denote the number of sheep each grazes on the common pasture. Assume that the benefit per sheep (in terms of mutton and wool) equals 300 - s A - s e implying that the total benefit from a flock of s A sheepis s A (300 - s A - s B ) and that the marginal benefit of an additional sheep (as one can use calculus to show or can take for granted) is 300 - 2s A - s e. Assume the (total and marginal) cost of grazing sheep is zero since the common can be freely used.
a. Compute the flock sizes and shepherds' total benefits in the Nash equilibrium.
b. Draw the best-response-function diagram corresponding to your solution.
c. Suppose A's benefit per sheep rises to 330 - s A - s B. Compute the new Nash equilibrium flock sizes. Show the change from the original to the new Nash equilibrium in your best-response-function diagram
a. Compute the flock sizes and shepherds' total benefits in the Nash equilibrium.
b. Draw the best-response-function diagram corresponding to your solution.
c. Suppose A's benefit per sheep rises to 330 - s A - s B. Compute the new Nash equilibrium flock sizes. Show the change from the original to the new Nash equilibrium in your best-response-function diagram

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
17
Why are Nash equilibria identified by the strategies rather than the payoffs involved?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
18
Choose a setting from student life. Try to model it as a game, with a set number of players, payoffs, and actions. Is it like any of the classic games studied in this chapter?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
19
Consider the indefinitely repeated Prisoners' Dilemma.
1. For what value of g does the repeated game become simply the stage game?
2. Suppose that at some point while playing the grim strategy, players relent and go back to the cooperative outcome (Silent). If this relenting were anticipated, how would it affect the ability to sustain the cooperative outcome?
1. For what value of g does the repeated game become simply the stage game?
2. Suppose that at some point while playing the grim strategy, players relent and go back to the cooperative outcome (Silent). If this relenting were anticipated, how would it affect the ability to sustain the cooperative outcome?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
20
How would you write down the game corresponding to the bar scene from A Beautiful Mind? What are the Nash equilibria of your game? Should the females be included as players in the setup along with the males?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
21
Consider the war over the new format for high-definition video disks discussed in Application 5.3, but shift the focus to the game (provided in the following table) between the two firms, Sony and Toshiba. 
a. Find the pure-strategy Nash equilibrium or equilibria.
b. Compute the mixed-strategy Nash equilibrium. As part of your answer, draw the best-response function diagram for the mixed strategies.
c. Suppose the game is played sequentially, with Sony moving first. What are Toshiba's contingent strategies? Write down the normal and extensive forms for the sequential version of the game.
d. Using the normal form for the sequential version of the game, solve for the Nash equilibria.
e. Identify the proper subgames in the extensive form for the sequential version of the game. Use backward induction to solve for the sub-game-perfect equilibrium. Explain why the other Nash equilibria of the sequential game are "unreasonable."

a. Find the pure-strategy Nash equilibrium or equilibria.
b. Compute the mixed-strategy Nash equilibrium. As part of your answer, draw the best-response function diagram for the mixed strategies.
c. Suppose the game is played sequentially, with Sony moving first. What are Toshiba's contingent strategies? Write down the normal and extensive forms for the sequential version of the game.
d. Using the normal form for the sequential version of the game, solve for the Nash equilibria.
e. Identify the proper subgames in the extensive form for the sequential version of the game. Use backward induction to solve for the sub-game-perfect equilibrium. Explain why the other Nash equilibria of the sequential game are "unreasonable."

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
22
One of Nash's classmates suggested that Nash was trying to convince the others to go after the brunettes so that Nash could have the blond for himself. Is this a Nash equilibrium? Are there others like it? How can one decide how a game will be played if there are multiple Nash equilibria?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
23
Which of the following activities might be represented as a zero-sum game? Which are clearly not zero sum?
a. Flipping a coin for $1
b. Playing blackjack
c. Choosing which candy bar to buy from a vendor
d. Reducing taxes through various ''creative accounting'' methods and seeking to avoid detection by the IRS
e. Deciding when to rob a particular house, knowing that the residents may adopt various countertheft strategies
a. Flipping a coin for $1
b. Playing blackjack
c. Choosing which candy bar to buy from a vendor
d. Reducing taxes through various ''creative accounting'' methods and seeking to avoid detection by the IRS
e. Deciding when to rob a particular house, knowing that the residents may adopt various countertheft strategies

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
24
Verify the mixed-strategy Nash equilibrium computed above for the penalty-kick game following the methods used for the Battle of the Sexes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
25
Suppose the Tragedy of the Commons involved three shepherds (A, B, and C). Suppose the benefit per sheep is 120 -s A - s B - s C , implying that, for example, A's total benefit is s A (120 - s A - s B - s C ) and marginal benefit is 120 - 2s A -s b - s c.
1. Solve the three equations that come from equating each of the three shepherds' marginal benefit of a sheep to the marginal cost (zero) to find the Nash quilibrium.
2. Compare the total number of sheep on the common with three shepherds to that with two.
1. Solve the three equations that come from equating each of the three shepherds' marginal benefit of a sheep to the marginal cost (zero) to find the Nash quilibrium.
2. Compare the total number of sheep on the common with three shepherds to that with two.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
26
Economists have studied mixed strategies in other sports, for example whether a tennis serve is aimed to the returner's backhand or forehand.2 Can you think of other sports settings involving mixed strategies? Can you think of settings outside of sports and games and besides the ones noted in the text?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
27
Two classmates A and B are assigned an extracredit group project. Each student can choose to Shirk or Work. If one or more players chooses Work, the project is completed and provides each with extra credit valued at 4 payoff units each. The cost of completing the project is that 6 total units of effort (measured in payoff units) is divided equally among all players who choose to Work and this is subtracted from their payoff. If both Shirk, they do not have to expend any effort but the project is not completed, giving each a payoff of 0. The teacher can only tell whether the project is completed and not which students contributed to it.
a. Write down the normal form for this game, assuming students choose to Shirk or Work simultaneously.
b. Find the Nash equilibrium or equilibria.
c. Does either player have a dominant strategy? What game from the chapter does this resemble?
a. Write down the normal form for this game, assuming students choose to Shirk or Work simultaneously.
b. Find the Nash equilibrium or equilibria.
c. Does either player have a dominant strategy? What game from the chapter does this resemble?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
28
Think about other standards wars. Can you identify factors determining the winning standard?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
29
Why is the Prisoners' Dilemma a ''dilemma'' for the players involved? How might they solve this dilemma through pregame discussions or postgame threats? If you were arrested and the D.A. tried this ploy, what would you do? Would it matter whether you were very close friends with your criminal accomplice?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
30
It was claimed that Nash equilibria tend to come in odd numbers, yet Table has an even number. The resolution of this seeming contradiction is that Nash equilibria come in odd numbers unless there are ties between payoffs in rows or columns. Show that an odd number of Nash equilibria result in Table if some of certain payoffs are tweaked to break ties.
Table After Bundling Blu-Ray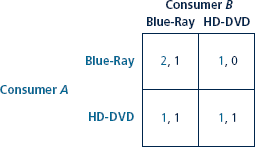
Table After Bundling Blu-Ray


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
31
Return to the Battle of the Sexes in Table Compute the mixed-strategy Nash equilibrium under the following modifications and compare it to the one computed in the text. Draw the corresponding best-response-function diagram for the mixed strategies.
a. Double all of the payoffs.
b. Double the payoff from coordinating on one's preferred activity from 2 to 4 but leave all other payoffs the same.
c. Change the payoff from choosing one's preferred activity alone (that is, not coordinating with one's spouse) from 0 to V for each but leave all the other payoffs the same.
TABLE Battle of the Sexes in Normal form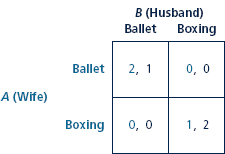
a. Double all of the payoffs.
b. Double the payoff from coordinating on one's preferred activity from 2 to 4 but leave all other payoffs the same.
c. Change the payoff from choosing one's preferred activity alone (that is, not coordinating with one's spouse) from 0 to V for each but leave all the other payoffs the same.
TABLE Battle of the Sexes in Normal form


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
32
As an experimenter, how would you choose the following aspects of experimental design? Are there any tradeoffs involved?
a. Size of the payoffs
b. Ability of subjects to see opponents
c. Playing the same game against the same opponent repeatedly
d. Informing subjects fully about the experimental design
a. Size of the payoffs
b. Ability of subjects to see opponents
c. Playing the same game against the same opponent repeatedly
d. Informing subjects fully about the experimental design

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
33
In Matching Pennies, suppose B plays the equilibrium mixed strategy of Heads with probability1/2 and Tails with probability 1/2. Use the formula for expected values to verify that A's expected payoff equals 0 from using any of the following strategies.
1. The pure strategy of Heads
2. The pure strategy of Tails
3. The mixed strategy of Heads with probability 1/2 and Tails with probability 1
4. The mixed strategy of Heads with probability 1/3 and Tails with probability 2/3
1. The pure strategy of Heads
2. The pure strategy of Tails
3. The mixed strategy of Heads with probability 1/2 and Tails with probability 1
4. The mixed strategy of Heads with probability 1/3 and Tails with probability 2/3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
34
The Battle of the Sexes is a coordination game. What coordination games arise in your experience? How do you go about solving coordination problems?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck
35
How would you construct an experiment involving the Battle of the Sexes? What theoretical issues might be interesting to test with your experiment?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 35 في هذه المجموعة.
فتح الحزمة
k this deck








