Deck 31: Alternating Current
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/51
العب
ملء الشاشة (f)
Deck 31: Alternating Current
1
Normalization: The wave function for a particle must be normalizable because
A) the particle must be somewhere.
B) the particle's charge must be conserved.
C) the particle cannot be in two places at the same time.
D) the particle's angular momentum must be conserved.
E) the particle's momentum must be conserved.
A) the particle must be somewhere.
B) the particle's charge must be conserved.
C) the particle cannot be in two places at the same time.
D) the particle's angular momentum must be conserved.
E) the particle's momentum must be conserved.
the particle must be somewhere.
2
Particle in a box: The smallest kinetic energy that an electron in a box (an infinite well) can have is zero.
False
3
Particle in a box: An electron is in an infinite square well (a box) that is 2.0 nm wide. The electron makes a transition from the  to the
to the  state, what is the wavelength of the emitted photon? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
state, what is the wavelength of the emitted photon? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
A) 880 nm
B) 750 nm
C) 610 nm
D) 1000 nm
E) 1100 nm
 to the
to the  state, what is the wavelength of the emitted photon? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
state, what is the wavelength of the emitted photon? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)A) 880 nm
B) 750 nm
C) 610 nm
D) 1000 nm
E) 1100 nm
880 nm
4
Particle in a box: The ground state energy of a particle in a one-dimensional infinite potential well of width 1.5 nm is 20 eV. The ground state energy of the same particle in a one-dimensional finite potential well with U0 = 0 in the region 0 < x < 1.5 nm, and U0 = 50 eV everywhere else, would be
A) less than 20 eV.
B) greater than 20 eV.
C) equal to 20 eV.
D) The particle would not have a ground state.
A) less than 20 eV.
B) greater than 20 eV.
C) equal to 20 eV.
D) The particle would not have a ground state.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
5
Harmonic oscillator: If an atom in a crystal is acted upon by a restoring force that is directly proportional to the distance of the atom from its equilibrium position in the crystal, then it is impossible for the atom to have zero kinetic energy.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
6
Particle in a box: A particle is confined to a one-dimensional box (an infinite well) on the x-axis between x = 0 and x = L. The potential height of the walls of the box is infinite. The normalized wave function of the particle, which is in the ground state, is given by ψ(x) = 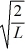 sin
sin 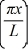 , with 0 ≤ x ≤ L. What is the probability of finding the particle between x = 0 and x = L/3?
, with 0 ≤ x ≤ L. What is the probability of finding the particle between x = 0 and x = L/3?
A) 0.20
B) 0.22
C) 0.24
D) 0.26
E) 0.28
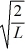 sin
sin 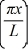 , with 0 ≤ x ≤ L. What is the probability of finding the particle between x = 0 and x = L/3?
, with 0 ≤ x ≤ L. What is the probability of finding the particle between x = 0 and x = L/3?A) 0.20
B) 0.22
C) 0.24
D) 0.26
E) 0.28

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
7
Normalization: Find the value of A to normalize the wave function ψ(x) = 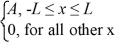
A) 1/L
B)
C) 1/L2
D) 1∙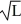
E) 1/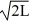
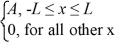
A) 1/L
B)

C) 1/L2
D) 1∙
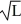
E) 1/
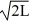

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
8
Particle in a box: An electron is in an infinite square well (a box) that is 8.9 nm wide. What is the ground state energy of the electron? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
A) 0.0048 eV
B) 0.0057 eV
C) 0.0066 eV
D) 0.0076 eV
E) 0.0085 eV
A) 0.0048 eV
B) 0.0057 eV
C) 0.0066 eV
D) 0.0076 eV
E) 0.0085 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
9
Normalization: A set of five possible wave functions is given below, where L is a positive real number. ψ1(x) = Ae-x, for all x ψ2(x) = A cos x, for all x
Ψ3(x) =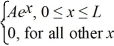 ψ4(x) =
ψ4(x) = 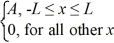 ψ5(x) =
ψ5(x) =  Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)
Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)
A) ψ1(x)
B) ψ2(x)
C) ψ3(x)
D) ψ4(x)
E) ψ5(x)
Ψ3(x) =
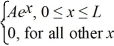 ψ4(x) =
ψ4(x) = 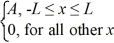 ψ5(x) =
ψ5(x) =  Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)
Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)A) ψ1(x)
B) ψ2(x)
C) ψ3(x)
D) ψ4(x)
E) ψ5(x)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
10
Particle in a box: A particle is confined to a one-dimensional box (an infinite well) on the x-axis between x = 0 and x = L. The potential height of the walls of the box is infinite. The normalized wave function of the particle, which is in the ground state, is given by ψ(x) = 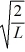 sin
sin  , with 0 ≤ x ≤ L. What is the maximum probability per unit length of finding the particle?
, with 0 ≤ x ≤ L. What is the maximum probability per unit length of finding the particle?
A) 1/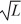
B)
C) 2/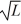
D) 1/L
E) 2/L
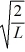 sin
sin  , with 0 ≤ x ≤ L. What is the maximum probability per unit length of finding the particle?
, with 0 ≤ x ≤ L. What is the maximum probability per unit length of finding the particle?A) 1/
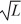
B)

C) 2/
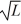
D) 1/L
E) 2/L

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
11
Normalization: Find the value of A to normalize the wave function ψ(x) = 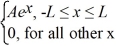
A)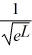
B)
C)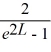
D)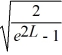
E)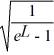
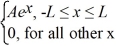
A)
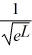
B)

C)
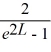
D)
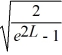
E)
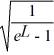

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
12
Normalization: The wave function for an electron that is confined to x ≥ 0 nm is
ψ(x) =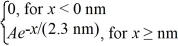 (a) What must be the value of A?
(a) What must be the value of A?
(b) What is the probability of finding the electron in the interval 1.15 nm ≤ x ≤ 1.84 nm?
ψ(x) =
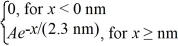 (a) What must be the value of A?
(a) What must be the value of A?(b) What is the probability of finding the electron in the interval 1.15 nm ≤ x ≤ 1.84 nm?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
13
Particle in a box: An electron is in an infinite square well that is 2.6 nm wide. What is the smallest value of the state quantum number n for which the energy level exceeds 100 eV? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
A) 43
B) 44
C) 45
D) 42
E) 41
A) 43
B) 44
C) 45
D) 42
E) 41

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
14
Quantum enganglement: Two entangled fermions each have equal probabilities of being in one of two states (state 1 or state 2). The fermions are separated so that no forces act between them. One of the fermions is then studied and found to be in state 1. What is the probability that, when studied, the second particle will also be found in state 1?
A) 0%
B) 33%
C) 50%
D) 67%
E) 100%
A) 0%
B) 33%
C) 50%
D) 67%
E) 100%

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
15
Particle in a box: A particle trapped in a one-dimensional finite potential well with U0 = 0 in the region 0 < x < L, and finite U0 everywhere else, has a ground state wavenumber, k. The ground state wavenumber for the same particle in an infinite one-dimensional potential well of width L, would be
A) less than k.
B) greater than k.
C) equal to k.
D) There is not enough information to determine.
A) less than k.
B) greater than k.
C) equal to k.
D) There is not enough information to determine.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
16
Normalization: The wave function for an electron that is confined to x ≥ 0 nm is
ψ(x) = a) What must be the value of b?
a) What must be the value of b?
(b) What is the probability of finding the electron in a 0.010 nm-wide region centered at x = 1.0 nm?
ψ(x) =
 a) What must be the value of b?
a) What must be the value of b?(b) What is the probability of finding the electron in a 0.010 nm-wide region centered at x = 1.0 nm?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
17
Probability: The square of the wave function of a particle, |ψ(x)|2, gives the probability of finding the particle at the point x.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
18
Particle in a box: An electron is bound in an infinite square-well potential (a box) on the x-axis. The width of the well is L and the well extends from x = 0.00 nm to 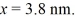 In its present state, the normalized wave function of the electron is given by: ψ(x) =
In its present state, the normalized wave function of the electron is given by: ψ(x) =
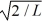 sin (2πx/L). What is the energy of the electron in this state? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
sin (2πx/L). What is the energy of the electron in this state? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
A) 0.10 eV
B) 0.052 eV
C) 0.13 eV
D) 0.078 eV
E) 0.026 eV
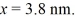 In its present state, the normalized wave function of the electron is given by: ψ(x) =
In its present state, the normalized wave function of the electron is given by: ψ(x) = 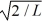 sin (2πx/L). What is the energy of the electron in this state? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)
sin (2πx/L). What is the energy of the electron in this state? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg, 1 eV = 1.60 × 10-19 J)A) 0.10 eV
B) 0.052 eV
C) 0.13 eV
D) 0.078 eV
E) 0.026 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
19
Particle in a box: An electron is in the ground state of an infinite well (a box) where its energy is 5.00 eV. In the next higher level, what would its energy be? (1 eV = 1.60 × 10-19 J)
A) 1.25 eV
B) 2.50 eV
C) 10.0 eV
D) 15.0 eV
E) 20.0 eV
A) 1.25 eV
B) 2.50 eV
C) 10.0 eV
D) 15.0 eV
E) 20.0 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
20
Probability: The probability density for an electron that has passed through an experimental apparatus is shown in the figure. If 4100 electrons pass through the apparatus, what is the expected number that will land in a 0.10 mm-wide strip centered at x = 0.00 mm? 
A) 140
B) 1400
C) 450
D) 45

A) 140
B) 1400
C) 450
D) 45

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
21
Tunneling: A 3.10-eV electron is incident on a 0.40-nm barrier that is 5.67 eV high. What is the probability that this electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mel = 9.11 × 10-31 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 1.4 × 10-3
B) 9.0 × 10-4
C) 1.0 × 10-3
D) 1.5 × 10-3
E) 1.2 × 10-3
A) 1.4 × 10-3
B) 9.0 × 10-4
C) 1.0 × 10-3
D) 1.5 × 10-3
E) 1.2 × 10-3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
22
Particle in a box: You want to have an electron in an energy level where its speed is no more than 66 m/s. What is the length of the smallest box (an infinite well) in which you can do this? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
A) 5.5 µm
B) 11 µm
C) 2.8 µm
D) 1.4 µm
A) 5.5 µm
B) 11 µm
C) 2.8 µm
D) 1.4 µm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
23
Particle in a box: A particle confined in a rigid one-dimensional box (an infinite well) of length 17.0 fm has an energy level 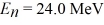 and an adjacent energy level En+1 = 37.5 MeV. What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)
and an adjacent energy level En+1 = 37.5 MeV. What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)
A) 1.50 MeV
B) 13.5 MeV
C) 0.500 MeV
D) 4.50 MeV
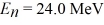 and an adjacent energy level En+1 = 37.5 MeV. What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)
and an adjacent energy level En+1 = 37.5 MeV. What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)A) 1.50 MeV
B) 13.5 MeV
C) 0.500 MeV
D) 4.50 MeV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
24
Particle in a box: You want to confine an electron in a box (an infinite well) so that its ground state energy is 5.0 × 10-18 J. What should be the length of the box? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
A) 0.11 nm
B) 0.22 nm
C) 0.15 nm
D) 0.18 nm
A) 0.11 nm
B) 0.22 nm
C) 0.15 nm
D) 0.18 nm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
25
Tunneling: An 80-eV electron impinges upon a potential barrier 100 eV high and 0.20 nm thick. What is the probability the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mproton = 1.67 × 10-27 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 0.027%
B) 2.7%
C) 0.27%
D) 2.8 × 10-4 %
E) 2.0 × 10-9 %
A) 0.027%
B) 2.7%
C) 0.27%
D) 2.8 × 10-4 %
E) 2.0 × 10-9 %

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
26
Tunneling: An electron with kinetic energy 2.80 eV encounters a potential barrier of height 4.70 eV. If the barrier width is 0.40 nm, what is the probability that the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mel = 9.11 × 10-31 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 3.5 × 10-3
B) 7.3 × 10-3
C) 1.4 × 10-2
D) 2.9 × 10-3
E) 3.5 × 10-2
A) 3.5 × 10-3
B) 7.3 × 10-3
C) 1.4 × 10-2
D) 2.9 × 10-3
E) 3.5 × 10-2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
27
Particle in a box: An electron is trapped in an infinite square well (a box) of width 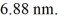 Find the wavelength of photons emitted when the electron drops from the n = 5 state to the n = 1 state in this system. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
Find the wavelength of photons emitted when the electron drops from the n = 5 state to the n = 1 state in this system. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
A) 6.49 μm
B) 5.45 μm
C) 5.91 μm
D) 7.07 μm
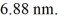 Find the wavelength of photons emitted when the electron drops from the n = 5 state to the n = 1 state in this system. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
Find the wavelength of photons emitted when the electron drops from the n = 5 state to the n = 1 state in this system. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)A) 6.49 μm
B) 5.45 μm
C) 5.91 μm
D) 7.07 μm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
28
Particle in a box: One fairly crude method of determining the size of a molecule is to treat the molecule as an infinite square well (a box) with an electron trapped inside, and to measure the wavelengths of emitted photons. If the photon emitted during the n = 2 to n = 1 transition has wavelength 1940 nm, what is the width of the molecule? (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
A) 1.33 nm
B) 1.12 nm
C) 1.21 nm
D) 1.45 nm
A) 1.33 nm
B) 1.12 nm
C) 1.21 nm
D) 1.45 nm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
29
Particle in a box: A 10.0-g bouncy ball is confined in a 8.3-cm-long box (an infinite well). If we model the ball as a point particle, what is the minimum kinetic energy of the ball? (h = 6.626 × 10-34 J ∙ s)
A) 8.0 ×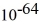 J
J
B) 3.2 ×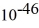 J
J
C) 1.3 × J
J
D) zero
A) 8.0 ×
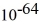 J
JB) 3.2 ×
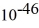 J
JC) 1.3 ×
 J
JD) zero

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
30
Particle in a box: An electron is confined in a one-dimensional box (an infinite well). Two adjacent allowed energies of the electron are 1.068 × 10-18 J and 1.352 × 10-18 J. What is the length of the box? (h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
A) 1.9 nm
B) 0.93 nm
C) 1.1 nm
D) 2.3 nm
A) 1.9 nm
B) 0.93 nm
C) 1.1 nm
D) 2.3 nm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
31
Particle in a box: The wave function of an electron in a rigid box (infinite well) is shown in the figure. If the electron energy 98.0 eV, what is the energy of the electron's ground state? ( mel = 9.11 × 10-31 kg) 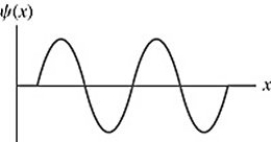
A) 6.13 eV
B) 3.92 eV
C) 10.9 eV
D) 24.5 eV

A) 6.13 eV
B) 3.92 eV
C) 10.9 eV
D) 24.5 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
32
Particle in a box: An electron is bound in an infinite well (a box) of width 0.10 nm. If the electron is initially in the n = 8 state and falls to the n = 7 state, find the wavelength of the emitted photon. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
33
Particle in a box: A one-dimensional finite potential well has potential energy U0 = 0 in the region 0 < x < 0.2 nm, and U0 = 15 eV everywhere else. A particle with which of the energies listed below would be localized (trapped) within the potential well? (Select all correct answers.)
A) 5 eV
B) 20 eV
C) 16 eV
D) 7 eV
E) None of the above.
A) 5 eV
B) 20 eV
C) 16 eV
D) 7 eV
E) None of the above.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
34
Tunneling: The energy of a proton is 1.0 MeV below the top of a 6.8-fm-wide energy barrier. What is the probability that the proton will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mproton = 1.67 × 10-27 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 0.051
B) 0.048
C) 0.056
D) 0.053
A) 0.051
B) 0.048
C) 0.056
D) 0.053

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
35
Tunneling: An 80-eV electron impinges upon a potential barrier 100 eV high and 0.20 nm thick. What is the probability the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mproton = 1.67 × 10-27 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 0.011%
B) 1.1%
C) 0.11%
D) 1.1 × 10-4 %
E) 7.7 × 10-10 %
A) 0.011%
B) 1.1%
C) 0.11%
D) 1.1 × 10-4 %
E) 7.7 × 10-10 %

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
36
Tunneling: An electron with kinetic energy 2.80 eV encounters a potential barrier of height 4.70 eV. If the barrier width is 0.40 nm, what is the probability that the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mel = 9.11 × 10-31 kg, h = 6.626 × 10-34 J ∙ s)
A) 1.4 × 10-2
B) 2.8 × 10-2
C) 5.5 × 10-2
D) 1.1 × 10-2
E) 1.4 × 10-1
A) 1.4 × 10-2
B) 2.8 × 10-2
C) 5.5 × 10-2
D) 1.1 × 10-2
E) 1.4 × 10-1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
37
Particle in a box: The lowest energy level of a particle confined to a one-dimensional region of space (a box, or infinite well) with fixed length L is E0. If an identical particle is confined to a similar region with fixed length L/ 6, what is the energy of the lowest energy level that the particles have in common? Express your answer in terms of E0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
38
Tunneling: The energy of a proton is 1.0 MeV below the top of a 1.2-MeV-high energy barrier that is 6.8 fm wide. What is the probability that the proton will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mproton = 1.67 × 10-27 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 11%
B) 9.1%
C) 14%
D) 7.5%
A) 11%
B) 9.1%
C) 14%
D) 7.5%

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
39
Tunneling: A 3.10-eV electron is incident on a 0.40-nm barrier that is 5.67 eV high. What is the probability that this electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, mel = 9.11 × 10-31 kg, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 0.56%
B) 0.35%
C) 0.40%
D) 0.25%
E) 0.48%
A) 0.56%
B) 0.35%
C) 0.40%
D) 0.25%
E) 0.48%

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
40
Particle in a box: An electron in an infinite potential well (a box) makes a transition from the n = 3 level to the ground state and in so doing emits a photon of wavelength 20.9 nm. (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, mel = 9.11 × 10-31 kg)
(a) What is the width of this well?
(b) What wavelength photon would be required to excite the electron from its original level to the next higher one?
(a) What is the width of this well?
(b) What wavelength photon would be required to excite the electron from its original level to the next higher one?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
41
Harmonic oscillator: The energy of a particle in the second EXCITED state of a harmonic oscillator potential is 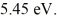 What is the classical angular frequency of oscillation of this particle? (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
What is the classical angular frequency of oscillation of this particle? (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 3.31 × 1015 rad/s
B) 2.08 × 1016 rad/s
C) 4.97 × 1015 rad/s
D) 6.95 × 1015 rad/s
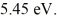 What is the classical angular frequency of oscillation of this particle? (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
What is the classical angular frequency of oscillation of this particle? (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)A) 3.31 × 1015 rad/s
B) 2.08 × 1016 rad/s
C) 4.97 × 1015 rad/s
D) 6.95 × 1015 rad/s

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
42
Harmonic oscillator: An electron is confined in a harmonic oscillator potential well. What is the longest wavelength of light that the electron can absorb if the net force on the electron behaves as though it has a spring constant of 74 N/m? (mel = 9.11 × 10-31 kg, c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 210 nm
B) 200 nm
C) 220 nm
D) 230 nm
A) 210 nm
B) 200 nm
C) 220 nm
D) 230 nm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
43
Harmonic oscillator: The lowest energy level of a certain quantum harmonic oscillator is 5.00 eV. What is the energy of the next higher level?
A) 7.50 eV
B) 10.0 eV
C) 15.0 eV
D) 20.0 eV
E) 50.0 eV
A) 7.50 eV
B) 10.0 eV
C) 15.0 eV
D) 20.0 eV
E) 50.0 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
44
Harmonic oscillator: An electron is confined in a harmonic oscillator potential well. A photon is emitted when the electron undergoes a 3→1 quantum jump. What is the wavelength of the emission if the net force on the electron behaves as though it has a spring constant of  (mel = 9.11 × 10-31 kg, c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
(mel = 9.11 × 10-31 kg, c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 290 nm
B) 150 nm
C) 190 nm
D) 580 nm
 (mel = 9.11 × 10-31 kg, c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
(mel = 9.11 × 10-31 kg, c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)A) 290 nm
B) 150 nm
C) 190 nm
D) 580 nm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
45
Harmonic oscillator: Find the wavelength of the photon emitted during the transition from the second EXCITED state to the ground state in a harmonic oscillator with a classical frequency of 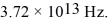 (c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
(c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 4.03 μm
B) 2.26 μm
C) 2.98 μm
D) 5.24 μm
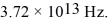 (c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
(c = 3.00 × 108 m/s, 1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)A) 4.03 μm
B) 2.26 μm
C) 2.98 μm
D) 5.24 μm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
46
Three dimensional potential well: A three-dimensional potential well has potential U0 = 0 in the region 0 < x < L, 0 < y < L, and 0 < z < L and infinite potential otherwise. The ground state energy of a particle in the well is E0. What is the energy of the first excited state, and what is the degeneracy of that state?
A) 2E0, single degeneracy
B) 2E0, triple degeneracy
C) 3E0, single degeneracy
D) 6E0, single degeneracy
E) 6E0, triple degeneracy
A) 2E0, single degeneracy
B) 2E0, triple degeneracy
C) 3E0, single degeneracy
D) 6E0, single degeneracy
E) 6E0, triple degeneracy

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
47
Harmonic oscillator: A lithium atom, mass 1.17 × 10-26 kg, vibrates with simple harmonic motion in a crystal lattice, where the effective force constant of the forces on the atom is k = 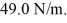 (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
(c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
(a) What is the ground state energy of this system, in eV?
(b) What is the wavelength of the photon that could excite this system from the ground state to the first excited state?
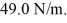 (c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
(c = 3.00 × 108 m/s, h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)(a) What is the ground state energy of this system, in eV?
(b) What is the wavelength of the photon that could excite this system from the ground state to the first excited state?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
48
Three dimensional potential well: A three-dimensional potential well has potential U0 = 0 in the region 0 < x < L, 0 < y < L, and 0 < z < 2L and infinite potential otherwise. The ground state energy of a particle in the well is E0. What is the energy of the first excited state, and what is the degeneracy of that state?
A) 2E0, single degeneracy
B) (4/3)E0, single degeneracy
C) 2E0, double degeneracy
D) (7/3)E0, double degeneracy
E) 3E0, triple degeneracy
A) 2E0, single degeneracy
B) (4/3)E0, single degeneracy
C) 2E0, double degeneracy
D) (7/3)E0, double degeneracy
E) 3E0, triple degeneracy

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
49
Three dimensional potential well: Model a hydrogen atom as a three-dimensional potential well with U0 = 0 in the region 0 < x < L, 0 < y < L, and 0 < z < L, and infinite otherwise, with L = 1.0 × 10-10 m. Which of the following is NOT one of the lowest three energy levels of an electron in this model?
A) 113 eV
B) 226 eV
C) 283 eV
D) 339 eV
A) 113 eV
B) 226 eV
C) 283 eV
D) 339 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
50
Harmonic oscillator: The atoms in a nickel crystal vibrate as harmonic oscillators with an angular frequency of 2.3 × 1013 rad/s. The mass of a nickel atom is 9.75 × 10-26 kg. What is the difference in energy between adjacent vibrational energy levels of nickel? (h = 6.626 × 10-34 J ∙ s, ħ = 1.055 × 10-34 J ∙ s, 1 eV = 1.60 × 10-19 J)
A) 0.015 eV
B) 0.019 eV
C) 0.023 eV
D) 0.027 eV
E) 0.031 eV
A) 0.015 eV
B) 0.019 eV
C) 0.023 eV
D) 0.027 eV
E) 0.031 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck
51
Harmonic oscillator: Calculate the ground state energy of a harmonic oscillator with a classical frequency of 3.68 × 1015 Hz. (1 eV = 1.60 × 10-19 J, ħ = 1.055 × 10-34 J ∙ s, h = 6.626 × 10-34 J ∙ s)
A) 7.62 eV
B) 15.2 eV
C) 11.4 eV
D) 5.71 eV
A) 7.62 eV
B) 15.2 eV
C) 11.4 eV
D) 5.71 eV

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 51 في هذه المجموعة.
فتح الحزمة
k this deck








