Deck 9: Applications of the Derivative
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/83
العب
ملء الشاشة (f)
Deck 9: Applications of the Derivative
1
Find the rate of change of x with respect to p.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Find the slope of the graph at the given point.
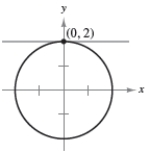
A)0
B)3
C)5
D)4
E)7

A)0
B)3
C)5
D)4
E)7
0
3
Find the of .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
A brick becomes dislodged from the Empire State Building (at a height of 1175 feet) and falls to the sidewalk below. Write the position s(t), velocity v(t), and acceleration a(t) as functions of time.
A) ; ;
B) ; ;
C) ; ;
D) ; ;
E) ; ;
A) ; ;
B) ; ;
C) ; ;
D) ; ;
E) ; ;

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
5
Find implicitly for
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the second derivative of the function.
A)
B)
C)
D)
E)None of the above
A)
B)
C)
D)
E)None of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
7
Find the slope of the graph at the given point.
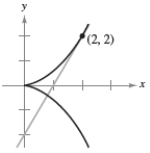
A)2
B)0
C)1
D)3
E)5

A)2
B)0
C)1
D)3
E)5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
8
Find for the equation by implicit differentiation and evaluate the derivative at the point .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
9
Find the third derivative of the function .
A)
B)
C)
D)
E) .
A)
B)
C)
D)
E) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find the second derivative for the function and solve the equation .
A)0
B)3
C)no solution
D)-3
E)
A)0
B)3
C)no solution
D)-3
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find the third derivative.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
12
Let x represent the units of labor and y the capital invested in a manufacturing process. When 135,540 units are produced, the relationship between labor and capital can be modeled by . Find the rate of change of y with respect to x when .
A)-2
B)0
C)3
D)-7
E)5
A)-2
B)0
C)3
D)-7
E)5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find for the equation .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
14
Find the second derivative for the function and solve the equation .
A)-3
B)3
C)0
D)32
E)12
A)-3
B)3
C)0
D)32
E)12

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
15
Find the indicated derivative. Find
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
16
Find the rate of change of x with respect to p.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find dy/dx for the following equation:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
18
Find the value for the function .
A)989,010
B)1,786,050
C)2,690,016
D)1,786,056
E)10,701,720
A)989,010
B)1,786,050
C)2,690,016
D)1,786,056
E)10,701,720

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
19
Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If
A)True
B)False. The product rule is
A)True
B)False. The product rule is

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find implicitly and explicitly(the explicit functions are shown on the graph) and show that the results are equivalent. Use the graph to estimate the slope of the tangent line at the labeled point. Then verify your result analytically by evaluating at the point. 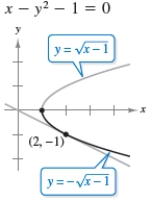
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
21
An airplane flying at an altitude of 5 miles passes directly over a radar antenna. When the airplane is 50 miles away (s = 50), the radar detects that the distance s is changing at a rate of 280 miles per hour. What is the speed of the airplane? Round your answer to the nearest integer.
A)281 mi/hr
B)271 mi/hr
C)563 mi/hr
D)141 mi/hr
E)135 mi/hr
A)281 mi/hr
B)271 mi/hr
C)563 mi/hr
D)141 mi/hr
E)135 mi/hr

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
22
A baseball diamond has the shape of a square with sides 90 feet long (see figure). A player running from second base to third base at a speed of 26 feet per second is 80 feet from third base. At what rate is the player's distance s from home plate changing? Round your answer to one decimal place. 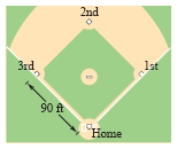
A)-50.4 feet/second
B)-0.2 feet/second
C)-0.7 feet/second
D)-17.3 feet/second
E)-1.9 feet/second

A)-50.4 feet/second
B)-0.2 feet/second
C)-0.7 feet/second
D)-17.3 feet/second
E)-1.9 feet/second

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
23
Volume and radius. Suppose that air is being pumped into a spherical balloon at a rate of At what rate is the radius of the balloon increasing when the radius is 3 in.?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
24
Use the graph of to identify at which of the indicated points the derivative changes from positive to negative. 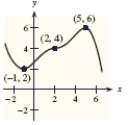
A)(5,6)
B)(-1,2), (2,4)
C)(-1,2), (5,6)
D)(-1,2)
E)(2,4), (5,6)

A)(5,6)
B)(-1,2), (2,4)
C)(-1,2), (5,6)
D)(-1,2)
E)(2,4), (5,6)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
25
Use the graph of to identify at which of the indicated points the derivative changes from negative to positive. 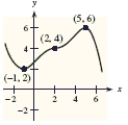
A)(2,4), (5,6)
B)(-1,2)
C)(2,4)
D)(-1,2), (2,4)
E)(-1,2), (5,6)

A)(2,4), (5,6)
B)(-1,2)
C)(2,4)
D)(-1,2), (2,4)
E)(-1,2), (5,6)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
26
Given find when x = 4 and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
27
Profit. Suppose that the monthly revenue and cost (in dollars) for x units of a product are At what rate per month is the profit changing if the number of units produced and sold is 100 and is increasing at a rate of 10 units per month?
A) per month
B) per month
C) per month
D) per month
E) per month
A) per month
B) per month
C) per month
D) per month
E) per month

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
28
The lengths of the edges of a cube are increasing at a rate of 7 ft/min. At what rate is the surface area changing when the edges are 22 ft long?
A)294 ft2/min
B)1848 ft2/min
C)924 ft2/min
D)6468 ft2/min
E)154 ft2/min
A)294 ft2/min
B)1848 ft2/min
C)924 ft2/min
D)6468 ft2/min
E)154 ft2/min

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
29
The radius r of a sphere is increasing at a rate of 3 inches per minute. Find the rate of change of volume when r = 17 inches. Round your answer to one decimal place.
A)3631.7 cubic inches per minute
B)20,579.5 cubic inches per minute
C)61,738.6 cubic inches per minute
D)10,895.0 cubic inches per minute
E)32,685.1 cubic inches per minute
A)3631.7 cubic inches per minute
B)20,579.5 cubic inches per minute
C)61,738.6 cubic inches per minute
D)10,895.0 cubic inches per minute
E)32,685.1 cubic inches per minute

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
30
Identify the open intervals where the function is increasing or decreasing.
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing on
D)decreasing on
E)none of the above
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing on
D)decreasing on
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
31
Both a function and its derivative are given. Use them to find all critical numbers.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
32
Assume that x and y are differentiable functions of t. Find dx/dt given that , , and
A)-3.00
B)2.67
C)1.50
D)-48.00
E)24.00
A)-3.00
B)2.67
C)1.50
D)-48.00
E)24.00

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
33
Assume that x and y are differentiable functions of t. Find dy/dt using the given values. for
A)152
B)58
C)116
D)150
E)75
A)152
B)58
C)116
D)150
E)75

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
34
Area. The radius, r, of a circle is decreasing at a rate of 2 centimeters per minute. Find the rate of change of area, A, when the radius is .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
35
Identify the open intervals where the function is increasing or decreasing.
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing on
D)decreasing on
E)none of the above
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing on
D)decreasing on
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
36
For the given function, find all critical numbers.
A)
B) and
C) and
D) and
E) and
A)
B) and
C) and
D) and
E) and

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
37
A retail sporting goods store estimates that weekly sales and weekly advertising costs are related by the equation . The current weekly advertising costs are $1500, and these costs are increasing at a rate of $140 per week. Find the current rate of change of weekly sales.
A)159,600 dollars per week
B)161,890 dollars per week
C)88,390 dollars per week
D)86,100 dollars per week
E)802,390 dollars per week
A)159,600 dollars per week
B)161,890 dollars per week
C)88,390 dollars per week
D)86,100 dollars per week
E)802,390 dollars per week

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
38
A point is moving along the graph of the function such that centimeters per second. Find dy/dt for the given values of x. (a) (b)
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
39
A point is moving along the graph of the function such that centimeters per second. Find dy/dt when .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
40
Boat docking. Suppose that a boat is being pulled toward a dock by a winch that is 24 ft above the level of the boat deck. If the winch is pulling the cable at a rate of 23 ft/min, at what rate is the boat approaching the dock when it is 32 ft from the dock? Use the figure below. 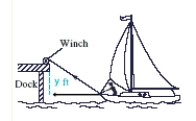
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
41
Suppose the number y of medical degrees conferred in the United States can be modeled by for , where t is the time in years, with corresponding to 1972. Use the test for increasing and decreasing functions to estimate the years during which the number of medical degrees is increasing and the years during which it is decreasing.
A)The number of medical degrees is increasing from 1972 to 1989 and 1997 to 2002, and decreasing during 1989 to 1997.
B)The number of medical degrees is increasing from 1972 to 1988 and 1996 to 2002, and decreasing during 1988 to 1996.
C)The number of medical degrees is increasing from 1972 to 1989 and 1996 to 2002, and decreasing during 1989 to 1996.
D)The number of medical degrees is increasing from 1972 to 1990 and 1996 to 2002, and decreasing during 1990 to 1996.
E)The number of medical degrees is increasing from 1972 to 1989 and 1995 to 2002, and decreasing during 1989 to 1995.
A)The number of medical degrees is increasing from 1972 to 1989 and 1997 to 2002, and decreasing during 1989 to 1997.
B)The number of medical degrees is increasing from 1972 to 1988 and 1996 to 2002, and decreasing during 1988 to 1996.
C)The number of medical degrees is increasing from 1972 to 1989 and 1996 to 2002, and decreasing during 1989 to 1996.
D)The number of medical degrees is increasing from 1972 to 1990 and 1996 to 2002, and decreasing during 1990 to 1996.
E)The number of medical degrees is increasing from 1972 to 1989 and 1995 to 2002, and decreasing during 1989 to 1995.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
42
Locate the absolute extrema of the function on the closed interval .
A)no absolute max; absolute min: f(1)= 2
B)absolute max: f(-2)= -34 ; absolute min: f(1)= 2
C)absolute max: f(1)= 2 ; no absolute min
D)absolute max: f(1)= 2 ; absolute min: f(-2)= -34
E)no absolute max or min
A)no absolute max; absolute min: f(1)= 2
B)absolute max: f(-2)= -34 ; absolute min: f(1)= 2
C)absolute max: f(1)= 2 ; no absolute min
D)absolute max: f(1)= 2 ; absolute min: f(-2)= -34
E)no absolute max or min

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
43
Locate the absolute extrema of the function on the closed interval [0,2].
A)absolute max: f(2)= 2 ; absolute min: f(1)= -2
B)absolute max: f(1)= -2 ; absolute min: f(2)= 2
C)absolute max: f(2)= 2 ; no absolute min
D)no absolute max; absolute min: f(2)= 2
E)no absolute max or min
A)absolute max: f(2)= 2 ; absolute min: f(1)= -2
B)absolute max: f(1)= -2 ; absolute min: f(2)= 2
C)absolute max: f(2)= 2 ; no absolute min
D)no absolute max; absolute min: f(2)= 2
E)no absolute max or min

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
44
Approximate the critical numbers of the function shown in the graph and determine whether the function has a relative maximum, a relative minimum, an absolute maximum, an absolute minimum, or none of these at each critical number on the interval shown. 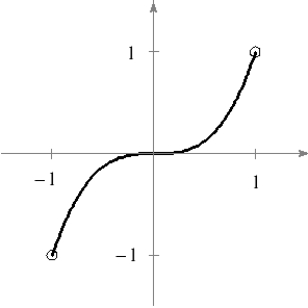
A)The critical number yields an absolute maximum and the critical number yields an absolute minimum..
B)Both the critical numbers & yield an absolute maximum.
C)The critical number yields an absolute minimum and the critical number yields an absolute maximum.
D)Both the critical numbers and yield an absolute minimum.
E)The critical number yields a relative minimum and the critical number yields a relative maximum.

A)The critical number yields an absolute maximum and the critical number yields an absolute minimum..
B)Both the critical numbers & yield an absolute maximum.
C)The critical number yields an absolute minimum and the critical number yields an absolute maximum.
D)Both the critical numbers and yield an absolute minimum.
E)The critical number yields a relative minimum and the critical number yields a relative maximum.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the open intervals on which the function is increasing or decreasing.
A)The function is increasing on the interval and decreasing on the interval .
B)The function is increasing on the interval and decreasing on the interval .
C)The function is increasing on the interval and decreasing on the interval .
D)The function is increasing on the interval and decreasing on the interval .
E)The function is increasing on the interval and decreasing on the interval .
A)The function is increasing on the interval and decreasing on the interval .
B)The function is increasing on the interval and decreasing on the interval .
C)The function is increasing on the interval and decreasing on the interval .
D)The function is increasing on the interval and decreasing on the interval .
E)The function is increasing on the interval and decreasing on the interval .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find the open intervals on which the function is increasing or decreasing.
A)The function is increasing on the interval , and decreasing on the intervals and .
B)The function is increasing on the interval , and decreasing on the intervals and .
C)The function is increasing on the interval , and decreasing on the intervals and .
D)The function is decreasing on the interval , and increasing on the intervals and .
E)The function is decreasing on the interval , and increasing on the intervals and .
A)The function is increasing on the interval , and decreasing on the intervals and .
B)The function is increasing on the interval , and decreasing on the intervals and .
C)The function is increasing on the interval , and decreasing on the intervals and .
D)The function is decreasing on the interval , and increasing on the intervals and .
E)The function is decreasing on the interval , and increasing on the intervals and .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find all relative minima of the given function.
A)
B)
C)
D) ,
E)no relative minima
A)
B)
C)
D) ,
E)no relative minima

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find the absolute extrema of the function on the interval .
A)The maximum of the function is 1 and the minimum of the function is 0.
B)The maximum of the function is 0 and the minimum of the function is -2.
C)The maximum of the function is -2 and the minimum of the function is 0.
D)The maximum of the function is 2 and the minimum of the function is 0.
E)The maximum of the function is 0 and the minimum of the function is 2.
A)The maximum of the function is 1 and the minimum of the function is 0.
B)The maximum of the function is 0 and the minimum of the function is -2.
C)The maximum of the function is -2 and the minimum of the function is 0.
D)The maximum of the function is 2 and the minimum of the function is 0.
E)The maximum of the function is 0 and the minimum of the function is 2.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
49
A fast-food restaurant determines the cost model, and revenue model, for where x is the number of hamburgers sold. Determine the intervals on which the profit function is increasing and on which it is decreasing.
A)The profit function is increasing on the interval and decreasing on the interval .
B)The profit function is increasing on the interval and decreasing on the interval .
C)The profit function is increasing on the interval and decreasing on the interval .
D)The profit function is increasing on the interval and decreasing on the interval .
E)The profit function is increasing on the interval and decreasing on the interval .
A)The profit function is increasing on the interval and decreasing on the interval .
B)The profit function is increasing on the interval and decreasing on the interval .
C)The profit function is increasing on the interval and decreasing on the interval .
D)The profit function is increasing on the interval and decreasing on the interval .
E)The profit function is increasing on the interval and decreasing on the interval .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find the x-values of all relative maxima of the given function.
A)
B)
C)
D)
E)no relative maxima
A)
B)
C)
D)
E)no relative maxima

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
51
For the function : (a) Find the critical numbers of f (if any);
(b) Find the open intervals where the function is increasing or decreasing; and
(c) Apply the First Derivative Test to identify all relative extrema.
Then use a graphing utility to confirm your results.
A) (a)
(b) increasing: ; decreasing:
(c) relative max: ; relative min:
B) (a)
(b) decreasing: ; increasing:
(c) relative min: ; relative max:
C) (a)
(b) increasing: ; decreasing:
(c) relative max: ; relative min:
D) (a)
(b) decreasing: ; increasing:
(c) relative min: ; relative max:
E) (a)
(b) increasing: ; decreasing:
(c) relative ; no relative min.
(b) Find the open intervals where the function is increasing or decreasing; and
(c) Apply the First Derivative Test to identify all relative extrema.
Then use a graphing utility to confirm your results.
A) (a)
(b) increasing: ; decreasing:
(c) relative max: ; relative min:
B) (a)
(b) decreasing: ; increasing:
(c) relative min: ; relative max:
C) (a)
(b) increasing: ; decreasing:
(c) relative max: ; relative min:
D) (a)
(b) decreasing: ; increasing:
(c) relative min: ; relative max:
E) (a)
(b) increasing: ; decreasing:
(c) relative ; no relative min.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
52
For the given function, find the relative minima.
A)
B)
C)
D)
E)no relative minima
A)
B)
C)
D)
E)no relative minima

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
53
Identify the open intervals where the function is increasing or decreasing.
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing: ; decreasing:
D)increasing: ; decreasing:
E)decreasing for all x
A)decreasing: ; increasing:
B)increasing: ; decreasing:
C)increasing: ; decreasing:
D)increasing: ; decreasing:
E)decreasing for all x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
54
For the given function, find the critical numbers.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
55
Find any critical numbers of the function , t < 14.
A)0
B)
C)
D)both A and B
E)both A and C
A)0
B)
C)
D)both A and B
E)both A and C

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
56
Locate the absolute extrema of the given function on the closed interval [-48,48].
A)absolute max: f(4)= 6
B)absolute min: f(-4)= -6
C)no absolute max
D)no absolute min
E)both A and D
F)both A and B
A)absolute max: f(4)= 6
B)absolute min: f(-4)= -6
C)no absolute max
D)no absolute min
E)both A and D
F)both A and B

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
57
Find the x-value at which the absolute minimum of f (x) occurs on the interval [a, b].
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
58
Graph a function on the interval having the following characteristics. Absolute maximum at Absolute minimum at Relative maximum at Relative minimum at
A)![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657d_bdc5_598eeacf2ff4_TB8692_11.jpg)
B)![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657e_bdc5_0dae315afb5c_TB8692_11.jpg)
C)![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657f_bdc5_173b53fb6bfd_TB8692_11.jpg)
D)![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_6580_bdc5_7f7f1fd6a5a4_TB8692_11.jpg)
E)![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_6581_bdc5_511d1fc3b5e9_TB8692_11.jpg)
A)
![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657d_bdc5_598eeacf2ff4_TB8692_11.jpg)
B)
![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657e_bdc5_0dae315afb5c_TB8692_11.jpg)
C)
![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_657f_bdc5_173b53fb6bfd_TB8692_11.jpg)
D)
![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_6580_bdc5_7f7f1fd6a5a4_TB8692_11.jpg)
E)
![<strong>Graph a function on the interval [ - 1,5 ] having the following characteristics. Absolute maximum at x = 4.75 Absolute minimum at x = - 1 Relative maximum at x = 0.3 Relative minimum at x = 3.1 </strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB8692/11eb99ec_121d_6581_bdc5_511d1fc3b5e9_TB8692_11.jpg)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find all relative maxima of the given function.
A)
B)
C)
D) ,
E)no relative maxima
A)
B)
C)
D) ,
E)no relative maxima

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
60
Find the absolute extrema of the function on the closed interval . Round your answer to two decimal places.
A)The maximum of the function is 1 and the minimum of the function is 0.
B)The maximum of the function is 2.52 and the minimum of the function is 1.
C)The maximum of the function is 2.52 and the minimum of the function is 0.
D)The maximum of the function is1 and the minimum of the function is 2.08.
E)The maximum of the function is 0 and the minimum of the function is 2.08.
A)The maximum of the function is 1 and the minimum of the function is 0.
B)The maximum of the function is 2.52 and the minimum of the function is 1.
C)The maximum of the function is 2.52 and the minimum of the function is 0.
D)The maximum of the function is1 and the minimum of the function is 2.08.
E)The maximum of the function is 0 and the minimum of the function is 2.08.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
61
The graph of f is shown. Graph f, f' and f'' on the same set of coordinate axes. 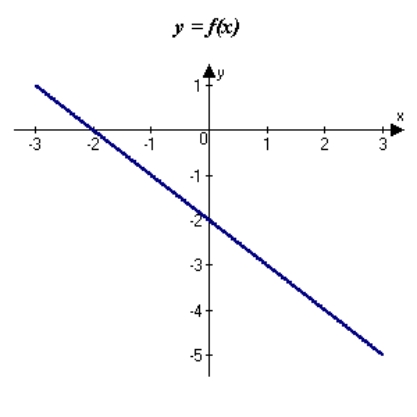
A)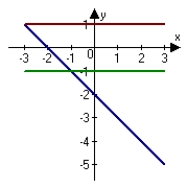
B)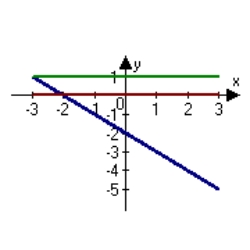
C)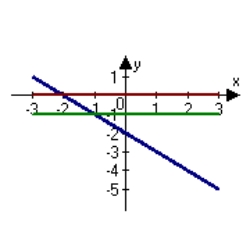
D)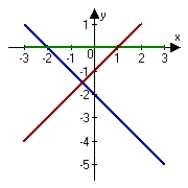
E)none of the above

A)

B)

C)

D)

E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
62
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 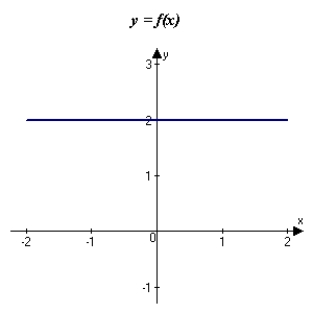
A)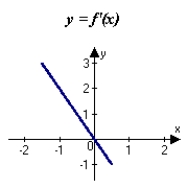
B)The derivative of f does not exist.
C)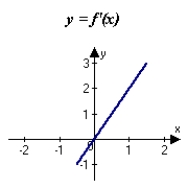
D)
E)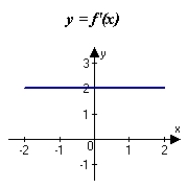

A)

B)The derivative of f does not exist.
C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
63
State the signs of and on the interval (0, 2). 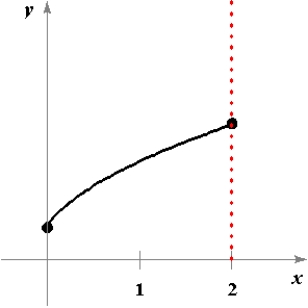
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
64
Find all relative extrema of the function . Use the Second-Derivative Test when applicable.
A)The relative minimum is and the relative maximum is .
B)The relative maximum is .
C)The relative minimum is .
D)The relative maximum is and the relative minima are and .
E)The relative minimum is and the relative maximum is .
A)The relative minimum is and the relative maximum is .
B)The relative maximum is .
C)The relative minimum is .
D)The relative maximum is and the relative minima are and .
E)The relative minimum is and the relative maximum is .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
65
Determine the open intervals on which the graph of is concave downward or concave upward.
A)concave downward on
B)concave downward on ; concave upward on
C)concave upward on ; concave downward on
D)concave downward on ; concave upward on
E)concave upward on ; concave downward on
A)concave downward on
B)concave downward on ; concave upward on
C)concave upward on ; concave downward on
D)concave downward on ; concave upward on
E)concave upward on ; concave downward on

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find all relative extrema of the function . Use the Second-Derivative Test when applicable.
A)The relative maximum is .
B)The relative minimum is .
C)The relative maximum is .
D)The relative minimum is
E)The relative maximum is .
A)The relative maximum is .
B)The relative minimum is .
C)The relative maximum is .
D)The relative minimum is
E)The relative maximum is .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
67
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 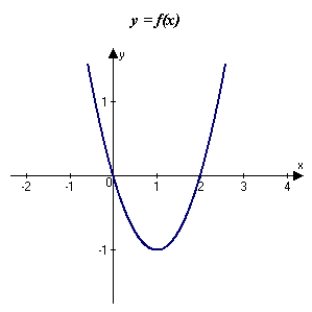
A)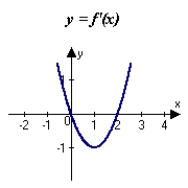
B)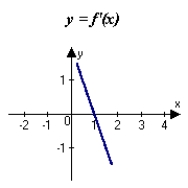
C)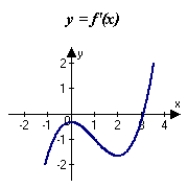
D)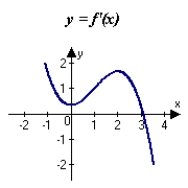
E)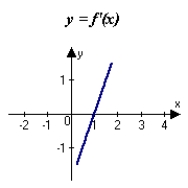

A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
68
Medication. The number of milligrams x of a medication in the bloodstream t hours after a dose is taken can be modeled by . Find the t-value at which x is maximum. Round your answer to two decimal places.
A)0 hours
B)3.61 hours
C)693.38 hours
D)5.61 hours
E)8.80 hours
A)0 hours
B)3.61 hours
C)693.38 hours
D)5.61 hours
E)8.80 hours

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
69
Sketch a graph of a function f having the following characteristics.
A)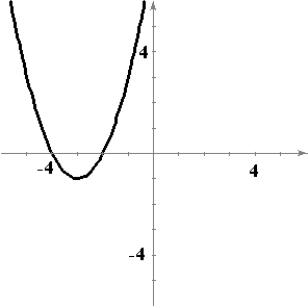
B)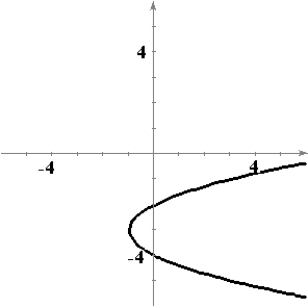
C)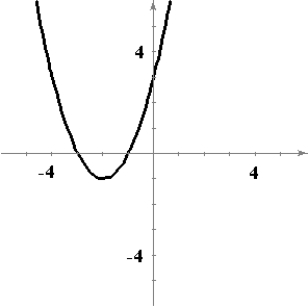
D)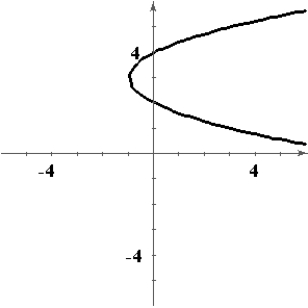
E)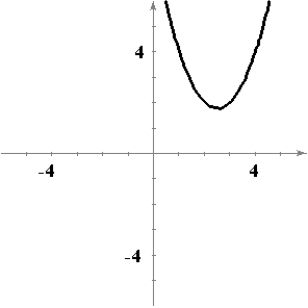
A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
70
Find all relative extrema of the function . Use the Second Derivative Test where applicable.
A)relative max: f(1)= -7
B)relative min: f(0)= -8
C)no relative max or min
D)both A and B
E)none of the above
A)relative max: f(1)= -7
B)relative min: f(0)= -8
C)no relative max or min
D)both A and B
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
71
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 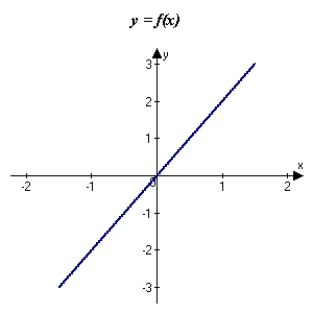
A)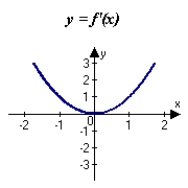
B)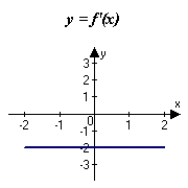
C)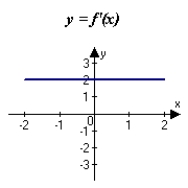
D)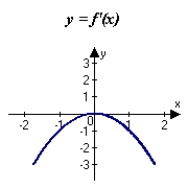
E)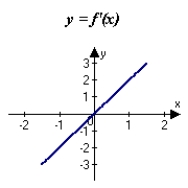

A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find all relative extrema of the function . Use the Second Derivative Test where applicable.
A)relative max:
B)relative min:
C)no relative min
D)no relative max
E)both A and C
F) both B and D
A)relative max:
B)relative min:
C)no relative min
D)no relative max
E)both A and C
F) both B and D

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
73
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 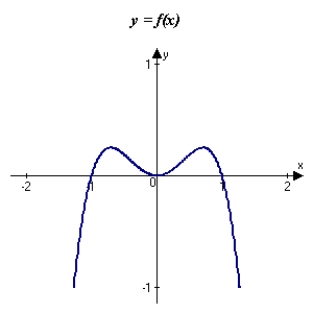
A)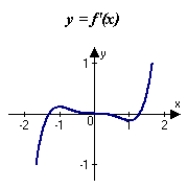
B)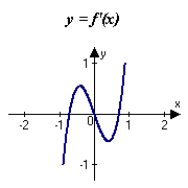
C)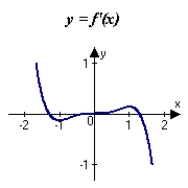
D)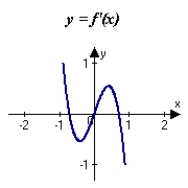
E)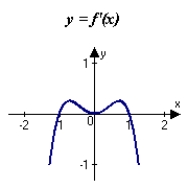

A)

B)

C)

D)

E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
74
Find the x-value at which the given function has a point of inflection.
A)
B)
C)
D)
E)no point of inflection
A)
B)
C)
D)
E)no point of inflection

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find the points of inflection and discuss the concavity of the function.
A)inflection point at ; concave downward on ; concave upward on
B)inflection point at ; concave upward on ; concave downward on
C)inflection point at ; concave downward on ; concave upward on
D)inflection point at ; concave upward on ; concave downward on
E)none of the above
A)inflection point at ; concave downward on ; concave upward on
B)inflection point at ; concave upward on ; concave downward on
C)inflection point at ; concave downward on ; concave upward on
D)inflection point at ; concave upward on ; concave downward on
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
76
Find all relative extrema of the function Use the Second Derivative Test where applicable.
A)relative max: ; no relative min
B)relative max: ; no relative min
C)no relative max or min
D)relative min: ; no relative max
E)relative min: ; no relative max
A)relative max: ; no relative min
B)relative max: ; no relative min
C)no relative max or min
D)relative min: ; no relative max
E)relative min: ; no relative max

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
77
A function and its graph are given. Use the second derivative to locate all x-values of points of inflection on the graph of . Check these results against the graph shown. 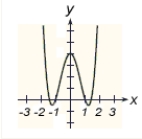
A)
B)
C)
D) ,
E) , ,

A)
B)
C)
D) ,
E) , ,

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
78
Determine the open intervals on which the graph of is concave downward or concave upward.
A)concave upward on ; concave downward on
B)concave downward on
C)concave upward on
D)concave downward on ; concave upward on
E)concave upward on ; concave downward on
A)concave upward on ; concave downward on
B)concave downward on
C)concave upward on
D)concave downward on ; concave upward on
E)concave upward on ; concave downward on

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
79
Medication. The number of milligrams x of a medication in the bloodstream t hours after a dose is taken can be modeled by . Find the maximum value of x. Round your answer to two decimal places.
A)3.46 mg
B)433.01 mg
C)952.63 mg
D)10.74 mg
E)1125.30 mg
A)3.46 mg
B)433.01 mg
C)952.63 mg
D)10.74 mg
E)1125.30 mg

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck
80
Suppose the resident population P(in millions) of the United States can be modeled by , where corresponds to 1800. Analytically find the minimum and maximum populations in the U.S. for .
A)The population is minimum at and maximum at .
B)The population is minimum at and maximum at .
C)The population is minimum at and maximum at .
D)The population is minimum at and maximum at .
E)The population is minimum at and maximum at .
A)The population is minimum at and maximum at .
B)The population is minimum at and maximum at .
C)The population is minimum at and maximum at .
D)The population is minimum at and maximum at .
E)The population is minimum at and maximum at .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 83 في هذه المجموعة.
فتح الحزمة
k this deck








