Deck 7: Polynomial Expressions

Question 1

Use a calculator to evaluate the expression. $19 ^ { 2 } - 16 ^ { 2 } - \left( 18 ^ { 2 } - 15 ^ { 2 } \right)$

A) 16
B) 9
C) $6$
D) 10
E) 11

Answer 1

$6$

Question 2

Multiply: $$( 2 v + 9 y ) ( 2 v - 9 y )$$

A) $4 v ^ { 2 } - 81 y ^ { 2 }$
B) $4 v ^ { 2 } + 36 v y - 81 y ^ { 2 }$
C) $4 v ^ { 2 } + 81 y ^ { 2 }$
D) $4 v ^ { 2 } - 18 y ^ { 2 }$
E) $4 v ^ { 2 } + 18 v + 81 y ^ { 2 }$

Answer 2

$4 v ^ { 2 } - 81 y ^ { 2 }$

Question 3

Multiply: $( x + 7 ) ( x - 7 )$

A) $x ^ { 2 } + 49$
B) $x ^ { 2 } + 14 x - 49$
C) $x ^ { 2 } - 49$
D) $x ^ { 2 } - 14 x + 49$
E) $x ^ { 2 } - 14$

Answer 3

$x ^ { 2 } - 49$

Question 4

Write the product after completing the table. Multiply $$\begin{array} { | l | l | l | } \hline \text { Multiply } & 3 x & - 2 \\\hline x & & \\\hline - 1 & & \\\hline\end{array}$$ (x - 1)(3x - 2) =

A) $3 x ^ { 2 } - 5 x + 2$
B) $5 x ^ { 2 } - 3 x - 2$
C) $3 x ^ { 2 } + 5 x + 2$
D) $2 x ^ { 2 } + 5 x - 3$
E) $2 x ^ { 2 } + 3 x + 5$

Question 5

Multiply: $$( 3 p + 7 ) ( 3 p - 7 )$$

A) $9 p ^ { 2 } - 49$
B) $9 p ^ { 2 } + 21 p - 49$
C) $9 p ^ { 2 } + 49$
D) $9 p ^ { 2 } - 14$
E) $9 p ^ { 2 } + 21 p + 49$

Question 6

Multiply: $$- x ( x + 4 )$$

A) $- x ^ { 2 } + 4 x$
B) $- x ^ { 2 } + 4$
C) $- x - 4 x$
D) $- x ^ { 2 } - 4 x$
E) $x ^ { 2 } + 4$

Question 7

Arrange the terms in descending order of exponents on x. $$x ^ { 2 } - x ^ { 4 } + 1 - x$$

A) $- x ^ { 4 } - x + x ^ { 2 } + 1$
B) $- x ^ { 4 } + x ^ { 2 } + 1 - x$
C) $1 - x ^ { 4 } - x + x ^ { 2 }$
D) $- x ^ { 4 } + x ^ { 2 } - x + 1$
E) $1 - x + x ^ { 2 } - x ^ { 4 }$

Question 8

Multiply: $$z ( z - 2 )$$

A) $z ^ { 2 } - 2 z$
B) $z ^ { 2 } - 2$
C) $z - 2 z$
D) $z ^ { 2 } + 2 z$
E) $z ^ { 2 } + 2$

Question 9

Find the perimeter of the following shape when a = 2.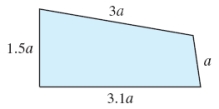

A) 8.6
B) 10
C) 12
D) 17.2
E) 19.2

Question 10

Write the product after completing the table. Multiply $$\begin{array} { | l | l | l | } \hline \text { Multiply } & x & - 1 \\\hline 2 x & & \\\hline + 3 & & \\\hline\end{array}$$ (x - 1)(2x + 3)

A) $x ^ { 2 } + 2 x - 3$
B) $2 x ^ { 2 } - x - 3$
C) $x ^ { 2 } + 2 x + 3$
D) $2 x ^ { 2 } + x + 3$
E) $2 x ^ { 2 } + x - 3$

Question 11

The perimeter of a rectangle is P = 4x + 6y. The length is 2x. What is the width?

A) 2x + 6y
B) 2x
C) 3y
D) 6y
E) 4x + 4y

Question 12

Multiply: $$- k ^ { 3 } \left( k ^ { 2 } - k \right)$$

A) $- k ^ { 5 } + k ^ { 3 }$
B) $- k ^ { 5 } - k ^ { 4 }$
C) $- k ^ { 5 } + k ^ { 4 }$
D) $- k ^ { 6 } + k ^ { 3 }$
E) $- k ^ { 6 } - k ^ { 3 }$

Question 13

Multiply: $$( y - 6 ) ( y + 14 )$$

A) $y ^ { 2 } + 20 y - 84$
B) $y ^ { 2 } + 8 y - 20$
C) $y ^ { 2 } + 20 y - 14$
D) $y ^ { 2 } + 8 y - 84$
E) $y ^ { 2 } + 6 y - 8$

Question 14

Multiply: $$( y - 8 ) ( y - 3 )$$

A) $y ^ { 2 } - 11 y + 24$
B) $y ^ { 2 } + 11 y - 3$
C) $y ^ { 2 } + 24$
D) $y ^ { 2 } - 11 y - 24$
E) $y ^ { 2 } - 8 y + 24$

Question 15

Multiply: $$y ^ { 2 } ( y - 5 )$$

A) $y ^ { 2 } - 5$
B) $y ^ { 3 } - 5 y ^ { 2 }$
C) $y ^ { 3 } - 5$
D) $y ^ { 2 } - 5 y ^ { 3 }$
E) $y ^ { 2 } - 5 y$

Question 16

Multiply: $$( 4 p + 3 ) ( 4 p - 3 )$$

A) $16 p ^ { 2 } - 12 p + 9$
B) $16 p ^ { 2 } + 12 p - 9$
C) $16 p ^ { 2 } + 9$
D) $16 p ^ { 2 } + 24 p + 9$
E) $16 p ^ { 2 } - 9$

Question 17

Multiply the expressions. The exercises can be done with algebra tiles. $$a ( a + 2 b )$$

A) $2 a + 2 a b$
B) $a ^ { 2 } + 2 b$
C) $a + 2 a b$
D) $a ^ { 2 } + 2 a b$
E) $a ^ { 2 } + a b$

Question 18

Find the perimeter of the shape when 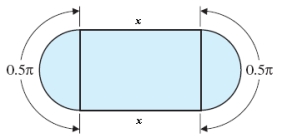$x = 2.5$

A) $2.5 + \pi$
B) $5 + \pi$
C) $5 + 5 \pi$
D) $5 + 2.5 \pi$
E) $2.5 + 0.5 \pi$

Question 19

Use the distributive property as needed and add or subtract like terms. Arrange the terms with descending order of exponents on y. $$\left( y ^ { 2 } + 3 y - 3 \right) - \left( - 8 + 9 y + 3 y ^ { 2 } \right)$$

A) $5 - 2 y ^ { 2 } - 6 y$
B) $- 2 y ^ { 2 } - 6 y + 5$
C) $- 2 y ^ { 2 } + 5 - 6 y$
D) $5 - 6 y - 2 y ^ { 2 }$
E) $- 2 y ^ { 2 } + 12 y - 11$

Question 20

Multiply: $$6 k ^ { 3 } \left( 3 k ^ { 2 } - 5 k \right)$$

A) $18 k ^ { 5 } - 30 k ^ { 3 }$
B) $18 k ^ { 5 } - 30 k ^ { 4 }$
C) $18 k ^ { 5 } - 5 k ^ { 4 }$
D) $18 k ^ { 6 } - 30 k ^ { 3 }$
E) $18 k ^ { 6 } - 5 k ^ { 3 }$

Question 21

Use any method to factor $x ^ { 2 } + 7 x - 18$

A) $( x - 2 ) ( x + 9 )$
B) $( x + 2 ) ( x - 9 )$
C) $( x - 2 ) ( x - 9 )$
D) $( x - 3 ) ( x + 6 )$
E) $( x + 3 ) ( x - 6 )$

Question 22

Multiply: $$( 2 y - 2 ) ( y + 3 )$$

A) $2 y ^ { 2 } + 8 y - 6$
B) $2 y ^ { 2 } + 6 y + 6$
C) $2 y ^ { 2 } + 4 y - 1$
D) $2 y ^ { 2 } + 8 y + 5$
E) $2 y ^ { 2 } + 4 y - 6$

Question 23

Use any method to factor $2 n ^ { 2 } + 5 n - 25$

A) $( 2 n + 5 ) ( n - 5 )$
B) $( 2 n - 5 ) ( n + 5 )$
C) $( 2 n - 5 ) ( n - 5 )$
D) $( 2 n - 25 ) ( n + 1 )$
E) $( 2 n + 25 ) ( n - 1 )$

Question 24

Complete the table and state the problem and factors described by the table. Factor $$\begin{array} { l l } x ^ { 2 } & + 5 x \\+ 4 x & + 20\end{array}$$

A) Factor $\begin{array}{ccc} & x^{2} & +5 \\x & x^{2} & +5 x \\+4 & +4 x & +20\end{array}$
$(x+5)(x+4)=x^{2}+9 x+20$
B) Factor $\begin{array}{ccc} & x & +5 \\x^{2} & x^{2} & +5 x \\+4 & +4 x & +20\end{array}$

$(x+5)(x+4)=x^{2}+9 x+20$
C) Factor $\begin{array}{ll}&x & +5 \\x & x^{2} & +5 x \\+4 & +4 x & +20\end{array}$

$(x+5)(x+4)=x^{2}+9 x+20$
D) Factor
$\begin{array}{ccc} & x & +5 \\x & x^{2} & +5 x \\+7 & +4 x & +20\end{array}$

$(x+5)(x+7)=x^{2}+12 x+35$
E) Factor
$\begin{array}{ccc} & x & +8 \\x & x^{2} & +5 x \\+4 & +4 x & +20\end{array}$

$(x+8)(x+4)=x^{2}+12 x+32$

Question 25

Use any method to factor $x ^ { 2 } - 19 x - 20$

A) $( x - 20 ) ( x - 1 )$
B) $( x - 5 ) ( x + 4 )$
C) $( x - 20 ) ( x + 1 )$
D) $( x + 5 ) ( x - 4 )$
E) $( x + 20 ) ( x - 1 )$

Question 26

Multiply: $$( y + 5 ) ( 4 y + 1 )$$

A) $4 y ^ { 2 } + 19 y + 5$
B) $4 y ^ { 2 } + 21 y + 1$
C) $4 y ^ { 2 } + 20 y + 5$
D) $4 y ^ { 2 } + 21 y + 5$
E) $4 y ^ { 2 } + 20 y + 4$

Question 27

Mentally factor the trinomial $$x ^ { 2 } + 15 x + 14$$

A) $( x + 2 ) ( x + 7 )$
B) $( x + 1 ) ( x + 14 )$
C) $( x - 2 ) ( x - 7 )$
D) $( x - 1 ) ( x - 14 )$
E) $( x - 1 ) ( x + 14 )$

Question 28

Mentally factor the trinomial $x ^ { 2 } - 10 x + 16$

A) $( x + 4 ) ( x + 4 )$
B) $( x - 4 ) ( x - 4 )$
C) $( x + 2 ) ( x - 8 )$
D) $( x - 2 ) ( x - 8 )$
E) $( x + 2 ) ( x + 8 )$

Question 29

Mentally factor the trinomials. $x ^ { 2 } + 36 x + 323$

A) $( x + 22 ) ( x + 19 )$
B) $( x + 22 ) ( x + 22 )$
C) $( x - 17 ) ( x + 19 )$
D) $( x - 19 ) ( x + 19 )$
E) $( x + 19 ) ( x + 17 )$

Question 30

Use any method to factor $x ^ { 2 } + 18 x + 81$

A) $( x - 9 ) ( x - 9 )$
B) $( x + 9 ) ( x - 9 )$
C) $( x + 3 ) ( x + 27 )$
D) $( x - 3 ) ( x - 27 )$
E) $( x + 9 ) ( x + 9 )$

Question 31

Use the order of operations to multiply the given expression. $$4 ( 2 - 3 x ) ^ { 2 }$$

A) $36 x ^ { 2 } - 24 x + 16$
B) $144 x ^ { 2 } - 96 x + 64$
C) $144 x ^ { 2 } - 192 x + 64$
D) $36 x ^ { 2 } - 48 x + 16$
E) $4 x ^ { 2 } - 12 x + 9$

Question 32

Multiply: $$( x + 4 ) ( x + 7 )$$

A) $x ^ { 2 } + 11 x + 28$
B) $x ^ { 2 } + 28 x + 11$
C) $x ^ { 2 } + 4 x + 11$
D) $x ^ { 2 } + 7 x + 4$
E) $x ^ { 2 } + 14 x + 16$

Question 33

Complete the trinomial product with mental multiplication. $$( x + 4 ) ( x - 9 ) = x ^ { 2 } - - { - } x - 36$$

A) 6
B) 3
C) 5
D) 8
E) 9

Question 34

Multiply: $$( 3 x - 3 ) ( 5 x - 5 )$$

A) $15 x ^ { 2 } - 18 x - 8$
B) $15 x ^ { 2 } - 30 x + 15$
C) $3 x ^ { 2 } + 15 x + 15$
D) $8 x ^ { 2 } - 15 x + 5$
E) $15 x ^ { 2 } - 18 x - 15$

Question 35

Use the order of operations to multiply the given expression. $$2 ( 3 x + 1 ) ^ { 2 }$$

A) $18 x ^ { 2 } + 6 x + 2$
B) $36 x ^ { 2 } + 6 x + 1$
C) $36 x ^ { 2 } + 12 x + 2$
D) $18 x ^ { 2 } + 12 x + 2$
E) $36 x ^ { 2 } + 12 x + 1$

Question 36

Complete the trinomial product with mental multiplication. $$( x - 1 ) ( x + 6 ) = x ^ { 2 } + \ldots x - 6$$

A) 4
B) 5
C) 7
D) 2
E) 9

Question 37

Factor: $4 a ^ { 2 } + 13 a + 10$

A) $( a + 2 ) ( 4 a - 5 )$
B) $( a + 2 ) ( 4 a + 5 )$
C) $( a - 2 ) ( 4 a + 5 )$
D) $( 4 a - 5 ) ( a - 2 )$
E) Nonfactorable over the integers

Question 38

Multiply: $$( 5 a + 3 ) ( 5 a + 7 )$$

A) $10 a ^ { 2 } + 15 a + 21$
B) $25 a ^ { 2 } + 50 a + 21$
C) $25 a ^ { 2 } + 35 a + 10$
D) $5 a ^ { 2 } + 38 a + 7$
E) $25 a ^ { 2 } + 20 a + 21$

Question 39

Mentally factor the trinomial $a ^ { 2 } + a - 56$

A) $( a - 7 ) ( a + 8 )$
B) $( a + 7 ) ( a - 8 )$
C) $( a - 7 ) ( a - 8 )$
D) $( a - 4 ) ( a + 14 )$
E) $( a + 4 ) ( a - 14 )$

Question 40

Multiply: $$( 9 x - 2 ) ( x - 7 )$$

A) $9 x ^ { 2 } - 61 x + 14$
B) $9 x ^ { 2 } - 65 x + 14$
C) $9 x ^ { 2 } + 63 x + 9$
D) $9 x ^ { 2 } - 18 x - 7$
E) $9 x ^ { 2 } + 9 x + 9$

Question 41

Factor: $10 z - 50$

A) $10 ( z - 5 )$
B) $10 ( z + 5 )$
C) $10 ( z - 50 )$
D) $50 ( z - 1 )$
E) $50 ( z + 10 )$

Question 42

Factor: $b ^ { 2 } - 25$

A) $( b + 5 ) ( b - 5 )$
B) $( b - 5 ) ^ { 2 }$
C) $( b + 5 ) ^ { 2 }$
D) $( 5 + b ) ( 5 - b )$
E) Nonfactorable over the integers

Question 43

Factor: $5 z ^ { 4 } - 20 z ^ { 2 }$

A) $4 z ^ { 2 } ( z - 5 )$
B) $5 z \left( z ^ { 2 } - 4 \right)$
C) $5 z ^ { 2 } \left( z ^ { 2 } - 4 \right)$
D) $4 z ^ { 2 } \left( z ^ { 2 } - 5 \right)$
E) $5 z ^ { 2 } \left( z ^ { 2 } - 20 \right)$

Question 44

Factor: $7 z ^ { 2 } - 70 z + 147$

A) $7 ( z + 7 ) ( z + 3 )$
B) $7 ( z - 7 ) ( z + 3 )$
C) $7 ( z + 7 ) ( z - 3 )$
D) $7 ( z - 7 ) ( z - 3 )$
E) Nonfactorable over the integers

Question 45

Factor mentally. Look for special products and greatest common factors. $4 x ^ { 2 } - 36$ One factor is:

A) (x $-$ 6)
B) (x + 6)
C) (x $-$ 9)
D) (x + 9)
E) 4

Question 46

Factor: $5 b ^ { 2 } - 27 b + 10$

A) $( b + 5 ) ( 5 b - 2 )$
B) $( b + 2 ) ( 5 b - 5 )$
C) $( b - 5 ) ( 5 b - 2 )$
D) $( b + 2 ) ( 5 b + 5 )$
E) Nonfactorable over the integers

Question 47

Factor: $- 4 c ^ { 2 } + 8 c + 60$

A) $( c - 3 ) ( - 4 c + 20 )$
B) $- 4 ( c + 3 ) ( c - 5 )$
C) $- 4 ( c + 3 ) ( c + 5 )$
D) $( - 4 c + 5 ) ( c + 12 )$
E) Nonfactorable over the integers

Question 48

Factor mentally. Look for special products and greatest common factors. $x ^ { 2 } + 100$ One factor is

A) (x + 10)
B) (x + 20)
C) (x + 5)
D) (x - 10)
E) It cannot be factored.

Question 49

Factor: $c ^ { 2 } + 6 c + 9$

A) $( c + 3 ) ( c - 3 )$
B) $( c - 3 ) ^ { 2 }$
C) $( c + 3 ) ^ { 2 }$
D) $( 3 + c ) ( 3 - c )$
E) Nonfactorable over the integers

Question 50

Factor: $6 z ^ { 3 } - 54 z ^ { 2 } + 108 z$

A) $6 z ( z + 6 ) ( z + 3 )$
B) $z ( 6 z - 36 ) ( z + 3 )$
C) $6 z ( z - 6 ) ( z - 3 )$
D) $6 ( z + 6 ) ( z - 3 )$
E) Nonfactorable over the integers

Question 51

Factor: $49 z ^ { 2 } + 28 z + 4$

A) $( 2 + 7 z ) ( 2 - 7 z )$
B) $( 7 z - 2 ) ^ { 2 }$
C) $( 7 z + 2 ) ^ { 2 }$
D) $( 7 z + 2 ) ( 7 z - 2 )$
E) Nonfactorable over the integers

Question 52

Factor: $64 x ^ { 2 } - 25$

A) $( 5 + 8 x ) ( 5 - 8 x )$
B) $( 8 x - 5 ) ^ { 2 }$
C) $( 8 x + 5 ) ^ { 2 }$
D) $( 8 x + 5 ) ( 8 x - 5 )$
E) Nonfactorable over the integers

Question 53

Factor: $7 x ^ { 4 } - 77 x ^ { 3 } + 196 x ^ { 2 }$

A) $7 x ^ { 2 } ( x + 7 ) ( x + 4 )$
B) $7 x ( x - 7 ) ( x - 4 )$
C) $7 x ^ { 2 } ( x - 7 ) ( x - 4 )$
D) $7 \left( x ^ { 2 } + 7 \right) \left( x ^ { 2 } - 4 \right)$
E) Nonfactorable over the integers

Question 54

Factor: $4 z ^ { 2 } - 20 z$

A) $4 ( z - 5 )$
B) $4 z ( z - 5 )$
C) $4 \left( z ^ { 2 } - 20 z \right)$
D) $4 z ( z - 20 )$
E) $20 z ( z - 4 )$

Question 55

Factor: $- 6 z ^ { 3 } + 60 z ^ { 2 } - 144 z$

A) $- 6 z ( z - 6 ) ( z - 4 )$
B) $z ( z - 6 ) ( 6 z - 24 )$
C) $6 z ( z - 6 ) ( z - 4 )$
D) $- 6 ( z + 6 ) ( z - 4 )$
E) Nonfactorable over the integers

Question 56

Factor: $z ^ { 2 } - 4 z - 4$

A) $( z + 2 ) ( z - 2 )$
B) $( z - 2 ) ^ { 2 }$
C) $( z + 2 ) ^ { 2 }$
D) $( 2 + z ) ( 2 - z )$
E) Nonfactorable over the integers

Question 57

Factor: $b ^ { 2 } - 4 b + 4$

A) $( b + 2 ) ( b - 2 )$
B) $( b - 2 ) ^ { 2 }$
C) $( b + 2 ) ^ { 2 }$
D) $( 2 + b ) ( 2 - b )$
E) Nonfactorable over the integers

Question 58

Factor: $2 c ^ { 2 } + 18 c + 36$

A) $( 2 c + 12 ) ( c - 3 )$
B) $2 ( c + 6 ) ( c - 3 )$
C) $2 ( c + 6 ) ( c + 3 )$
D) $( 2 c + 12 ) ( 3 c + 1 )$
E) Nonfactorable over the integers

Question 59

Use any method to factor $3 a ^ { 2 } - 17 a - 6$

A) $( 3 a - 1 ) ( a + 6 )$
B) $( 3 a - 1 ) ( a - 6 )$
C) $( 3 a + 2 ) ( a - 3 )$
D) $( 3 a + 1 ) ( a - 6 )$
E) $( 3 a - 2 ) ( a + 3 )$

Question 60

Factor: $7 y ^ { 3 } + 15 y ^ { 2 }$

A) $y \left( 15 y ^ { 2 } + 7 \right)$
B) $y \left( 7 y ^ { 2 } + 15 \right)$
C) $y ^ { 2 } ( 15 y + 7 )$
D) $y ^ { 2 } ( 7 y + 15 )$
E) $y ^ { 2 } \left( 7 y ^ { 2 } + 15 y \right)$

Question 61

Factor: $6 - 18 z ^ { 2 }$

A) $6 \left( 3 z ^ { 2 } + 1 \right)$
B) $6 \left( z ^ { 2 } + 18 \right)$
C) $6 \left( 3 - z ^ { 2 } \right)$
D) $18 \left( 6 - z ^ { 2 } \right)$
E) $6 \left( 1 - 3 z ^ { 2 } \right)$

Question 62

Using the appropriate property. Leave answers without denominators. Assume all expressions are defined. $\frac { x ^ { 8 } } { x ^ { - 3 } }$

A) $x ^ { 11 }$
B) $x ^ { 5 }$
C) $x ^ { - 5 }$
D) $x ^ { 8 }$
E) $x ^ { 3 }$

Question 63

Write the number 48,000,000,000 in scientific notation.

A) $48 \times 10 ^ { 9 }$
B) $4.8 \times 10 ^ { 9 }$
C) $4.8 \times 10 ^ { 10 }$
D) $0.48 \times 10 ^ { 11 }$
E) $4.8 \times 10 ^ { 11 }$

Question 64

Write the mass of Pluto, which is approximately 14,000,000,000,000,000,000,000 kg, in scientific notation.

A) $1.4 \times 10 ^ { 24 }$
B) $1.4 \times 10 ^ { 23 }$
C) $1.4 \times 10 ^ { 21 }$
D) $1.4 \times 10 ^ { 22 }$
E) $1.4 \times 10 ^ { 20 }$

Question 65

Simplify the expression without a calculator. $6 ^ { 0 }$

A) $7$
B) $9$
C) 1
D) $8$
E) 0

Question 66

Simplify the expression without a calculator. $3 ^ { - 6 }$

A) $\frac { 1 } { 730 }$
B) $\frac { 1 } { 728 }$
C) $\frac { 1 } { 731 }$
D) $\frac { 1 } { 729 }$
E) $\frac { 1 } { 732 }$

Question 67

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { a } { b ^ { 2 } } \right) ^ { - 9 }$

A) $\frac { b ^ { 9 } } { a ^ { 18 } }$
B) $\frac { b } { a ^ { 18 } }$
C) $\frac { a ^ { 9 } } { b ^ { 18 } }$
D) $- \frac { b ^ { 18 } } { a ^ { 2 } }$
E) $\frac { b ^ { 18 } } { a ^ { 9 } }$

Question 68

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { 2 c } { a ^ { 4 } b } \right) ^ { - 3 }$

A) $\frac { 8 c } { a ^ { 4 } b }$
B) $\frac { a ^ { 12 } b ^ { 3 } } { 8 c ^ { 3 } }$
C) $\frac { 2 c } { a ^ { 4 } b }$
D) $\frac { 8 c ^ { 3 } } { a ^ { 12 } b ^ { 3 } }$
E) $\frac { a ^ { 12 } b ^ { 3 } } { 2 c ^ { 3 } }$

Question 69

Using the appropriate property and then check with a calculator. Leave answers without denominators. $\frac { 10 ^ { - 9 } } { 10 ^ { \gamma } }$

A) $10 ^ { 16 }$
B) $10 ^ { - 2 }$
C) $10 ^ { 2 }$
D) $10 ^ { - 16 }$
E) $10 ^ { 7 }$

Question 70

Mentally approximate the product without a calculator. $\left( 6 \times 10 ^ { 14 } \right) \left( 3 \times 10 ^ { 20 } \right)$

A) $18 \times 10 ^ { 50 }$
B) $18 \times 10 ^ { 35 }$
C) $9 \times 10 ^ { 34 }$
D) $1.8 \times 10 ^ { 33 }$
E) $1.8 \times 10 ^ { 35 }$

Question 71

Estimate the quotient without a calculator. $\left( 8 \times 10 ^ { 16 } \right) \div \left( 2 \times 10 ^ { 9 } \right)$

A) $4 \times 10 ^ { 7 }$
B) $4 \times 10 ^ { 25 }$
C) $16 \times 10 ^ { 7 }$
D) $4 \times 10 ^ { 14 }$
E) $7 \times 10 ^ { 7 }$

Question 72

Estimate the product without a calculator. $\left( 3 \times 10 ^ { 16 } \right) \left( 3 \times 10 ^ { 20 } \right)$

A) $9 \times 10 ^ { 50 }$
B) $9 \times 10 ^ { 36 }$
C) $6 \times 10 ^ { 36 }$
D) $6 \times 10 ^ { 320 }$
E) $9 \times 10 ^ { 320 }$

Question 73

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { 4 a ^ { 2 } } { c } \right) ^ { - 2 }$

A) $\frac { c ^ { 2 } } { 8 a ^ { 4 } }$
B) $\frac { c ^ { 2 } } { 16 a ^ { 2 } }$
C) $\frac { c ^ { 2 } } { 16 a ^ { 4 } }$
D) $\frac { c } { 8 a ^ { 2 } }$
E) $\frac { c } { 16 a ^ { 2 } }$

Question 74

Using the appropriate property and then check with a calculator. Leave answers without denominators. $\left( 2 ^ { - 4 } \right) ^ { - 8 }$

A) $2 ^ { 32 }$
B) $2 ^ { 12 }$
C) $2 ^ { - 32 }$
D) $2 ^ { - 12 }$
E) $2 ^ { - 4 }$

Question 75

Write the number 0.00051 in scientific notation.

A) $0.51 \times 10 ^ { - 3 }$
B) $5.1 \times 10 ^ { - 3 }$
C) $5.1 \times 10 ^ { - 4 }$
D) $51 \times 10 ^ { - 5 }$
E) $5.1 \times 10 ^ { - 6 }$

Question 76

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { c } { a } \right) ^ { 0 }$

A) $\left( \frac { \mathrm { c } } { \mathrm { a } } \right)$
B) $\left( \frac { c } { a } \right) ^ { - 1 }$
C) $\left( \frac { c } { a } \right) ^ { 2 }$
D) 0
E) 1

Question 77

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { x } { 2 y } \right) ^ { 2 }$

A) $\frac { x ^ { 2 } } { 4 y ^ { 2 } }$
B) $\frac { x } { 2 y }$
C) $\frac { x ^ { 2 } } { 4 y }$
D) $\frac { x } { 4 y ^ { 2 } }$
E) $\frac { x ^ { 2 } } { 2 y ^ { 2 } }$

Question 78

Simplify the expression. Remove all negative and zero exponents. Assume the expression is defined. $\left( \frac { \mathrm { c } } { \mathrm { gf } } \right) ^ { - 1 }$

A) $\frac { \mathrm { cg } } { \mathrm { f } }$
B) $\frac { \mathrm { c } } { \mathrm { gf } }$
C) $\frac { g } { c f }$
D) $\frac { \mathrm { gf } } { \mathrm { c } }$
E) $\frac { \mathrm { cg } } { \mathrm { f } }$ .

Question 79

Simplify the expressions. Remove all negative and zero exponents. Assume all expressions are defined. $\frac { a ^ { 2 } b ^ { - 1 } } { a ^ { - 1 } b ^ { 7 } }$

A) $\frac { b ^ { 3 } } { a ^ { 8 } }$
B) $\frac { a ^ { 2 } } { b ^ { 7 } }$
C) $\frac { b ^ { 8 } } { a ^ { 3 } }$
D) $\frac { b ^ { 2 } } { a ^ { 7 } }$
E) $\frac { a ^ { 3 } } { b ^ { 8 } }$

Question 80

The electric charge on an electron is 0.00000000000000000025 coulomb. Write this number in scientific notation.

A) $2.5 \times 10 ^ { - 19 }$ coulomb
B) $2.5 \times 10 ^ { - 18 }$ coulomb
C) $25 \times 10 ^ { - 20 }$ coulomb
D) $0.25 \times 10 ^ { - 18 }$ coulomb
E) $2.5 \times 10 ^ { - 20 }$ coulomb