Deck 8: Applications of Integration
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/139
العب
ملء الشاشة (f)
Deck 8: Applications of Integration
1
The equations y = x3, y = 0, and x = 1 define the bounds of a plane region. Find the volume of the solid obtained by rotating the region about the x-axis.
A)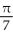 cubic units
cubic units
B)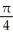 cubic units
cubic units
C)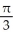 cubic units
cubic units
D)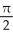 cubic units
cubic units
E)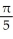 cubic units
cubic units
A)
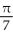 cubic units
cubic unitsB)
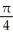 cubic units
cubic unitsC)
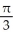 cubic units
cubic unitsD)
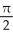 cubic units
cubic unitsE)
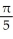 cubic units
cubic units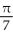 cubic units
cubic units 2
The equations x = 2, x = 4, y = 1/x, and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
A)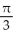 cubic units
cubic units
B)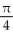 cubic units
cubic units
C)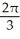 cubic units
cubic units
D)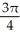 cubic units
cubic units
E)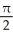 cubic units
cubic units
A)
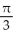 cubic units
cubic unitsB)
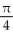 cubic units
cubic unitsC)
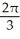 cubic units
cubic unitsD)
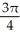 cubic units
cubic unitsE)
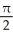 cubic units
cubic units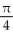 cubic units
cubic units 3
Find the volume of the solid obtained by rotating about the x-axis the region lying under the curve 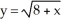 above the x-axis and to the left of the y-axis.
above the x-axis and to the left of the y-axis.
A) 32 cubic units
B) 16 cubic units
C) 64 cubic units
D) 4 cubic units
E) 25 cubic units
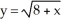 above the x-axis and to the left of the y-axis.
above the x-axis and to the left of the y-axis.A) 32 cubic units
B) 16 cubic units
C) 64 cubic units
D) 4 cubic units
E) 25 cubic units
32 cubic units
4
Find the volume of the solid obtained by rotating about the x-axis the plane region lying under the x-axis and above the curve y = x2 - 2x.
A)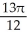 cubic units
cubic units
B)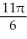 cubic units
cubic units
C)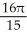 cubic units
cubic units
D)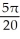 cubic units
cubic units
E)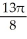 cubic units
cubic units
A)
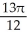 cubic units
cubic unitsB)
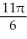 cubic units
cubic unitsC)
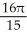 cubic units
cubic unitsD)
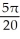 cubic units
cubic unitsE)
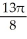 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
5
The region R is bounded by y = ln x, y = 0, x = 1, and x = 2. Find the volume of the solid obtained by revolving R about the y-axis.
A)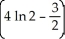 cubic units
cubic units
B)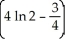 cubic units
cubic units
C)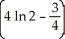 cubic units
cubic units
D)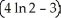 cubic units
cubic units
E)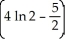 cubic units
cubic units
A)
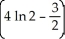 cubic units
cubic unitsB)
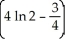 cubic units
cubic unitsC)
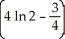 cubic units
cubic unitsD)
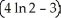 cubic units
cubic unitsE)
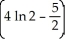 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the volume of a solid generated when the region under the curve y = sin x and above the x-axis from x = 0 to x = is rotated about the x-axis.
A)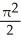 cubic units
cubic units
B)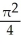 cubic units
cubic units
C)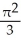 cubic units
cubic units
D)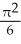 cubic units
cubic units
E)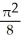 cubic units
cubic units
A)
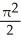 cubic units
cubic unitsB)
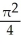 cubic units
cubic unitsC)
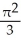 cubic units
cubic unitsD)
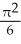 cubic units
cubic unitsE)
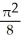 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
7
Find the volume of a solid generated when the region under the curve y = sin x and above the x-axis from x = 0 to x = is rotated about the y-axis.
A) 2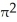 cubic units
cubic units
B)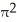 cubic units
cubic units
C) 3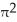 cubic units
cubic units
D)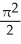 cubic units
cubic units
E) 4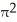 cubic units
cubic units
A) 2
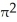 cubic units
cubic unitsB)
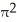 cubic units
cubic unitsC) 3
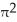 cubic units
cubic unitsD)
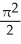 cubic units
cubic unitsE) 4
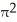 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
8
The equations x = -1, x = 0, y = 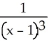 , and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
, and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
A)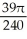 cubic units
cubic units
B)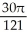 cubic units
cubic units
C)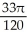 cubic units
cubic units
D)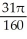 cubic units
cubic units
E)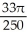 cubic units
cubic units
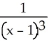 , and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.
, and y = 0 define the bounds of a region of the plane. Find the volume of the solid obtained by rotating the region about the x-axis.A)
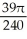 cubic units
cubic unitsB)
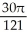 cubic units
cubic unitsC)
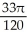 cubic units
cubic unitsD)
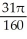 cubic units
cubic unitsE)
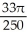 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
9
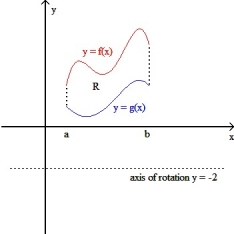
If R is the region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b (as shown in the figure below), then the volume V of the solid generated by revolving the region R about the line y = -2 is V = 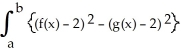 dx.
dx.
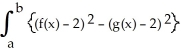 dx.
dx.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
10
The equations y2 = 4x and x2 = 4y define the bounds of a plane region. Find the volume of the solid obtained by rotating the region to the right of the curve y2 = 4x and above the curve x2 = 4y about
(a) the x-axis and
(b) the y-axis.
A) (a)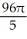 cubic units, (b)
cubic units, (b) 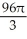 cubic units
cubic units
B) (a)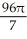 cubic units, (b)
cubic units, (b) 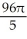 cubic units
cubic units
C) (a)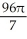 cubic units, (b)
cubic units, (b) 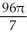 cubic units
cubic units
D) (a)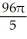 cubic units, (b)
cubic units, (b) 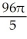 cubic units
cubic units
E) (a)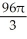 cubic units, (b)
cubic units, (b) 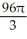 cubic units
cubic units
(a) the x-axis and
(b) the y-axis.
A) (a)
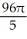 cubic units, (b)
cubic units, (b) 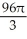 cubic units
cubic unitsB) (a)
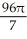 cubic units, (b)
cubic units, (b) 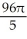 cubic units
cubic unitsC) (a)
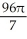 cubic units, (b)
cubic units, (b) 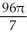 cubic units
cubic unitsD) (a)
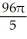 cubic units, (b)
cubic units, (b) 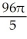 cubic units
cubic unitsE) (a)
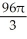 cubic units, (b)
cubic units, (b) 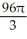 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find the volumes of solids generated when the ellipse 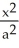 +
+ 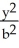 = 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.
= 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.
A)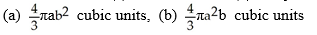
B)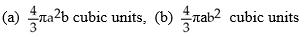
C)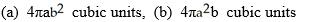
D)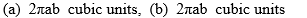
E)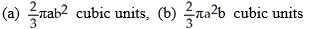
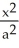 +
+ 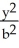 = 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.
= 1 (where a > 0 and b > 0) is rotated about (a) the x-axis and (b) the y-axis.A)
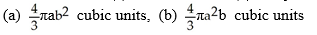
B)
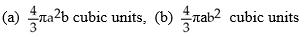
C)
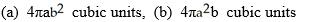
D)
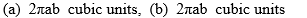
E)
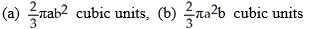

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
12
Find the volume of the solid obtained by rotating the region inside the circle x2 + y2 = 6 and above the parabola y = x2 about the x-axis.
A)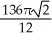 cubic units
cubic units
B)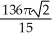 cubic units
cubic units
C)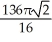 cubic units
cubic units
D)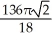 cubic units
cubic units
E)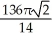 cubic units
cubic units
A)
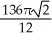 cubic units
cubic unitsB)
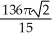 cubic units
cubic unitsC)
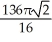 cubic units
cubic unitsD)
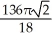 cubic units
cubic unitsE)
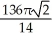 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find the volume of the solid obtained by rotating the region inside the circle x2 + y2 = 6 and above the parabola y = x2 about the y-axis.
A) 8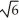 -
- 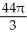 cubic units
cubic units
B) 4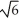 -
- 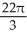 cubic units
cubic units
C) 4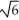 -
- 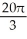 cubic units
cubic units
D) 8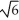 -
- 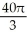 cubic units
cubic units
E) 2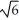 -
- 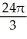 cubic units
cubic units
A) 8
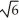 -
- 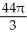 cubic units
cubic unitsB) 4
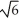 -
- 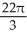 cubic units
cubic unitsC) 4
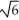 -
- 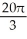 cubic units
cubic unitsD) 8
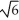 -
- 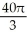 cubic units
cubic unitsE) 2
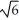 -
- 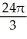 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
14
The region R is the portion of the first quadrant that is below the parabola y2 = 8x and above the hyperbola y2 - x2 = 15. Find the volume of the solid obtained by revolving R about the x-axis.
A)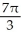 cubic units
cubic units
B)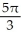 cubic units
cubic units
C)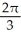 cubic units
cubic units
D)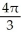 cubic units
cubic units
E)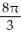 cubic units
cubic units
A)
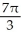 cubic units
cubic unitsB)
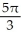 cubic units
cubic unitsC)
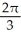 cubic units
cubic unitsD)
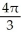 cubic units
cubic unitsE)
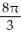 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
15
Find the volume of the solid generated by revolving the triangular region bounded by the lines y = x, y = -x, and x = a (where a > 0) about its edge x = a.
A)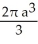 cubic units
cubic units
B)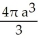 cubic units
cubic units
C)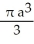 cubic units
cubic units
D)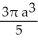 cubic units
cubic units
E)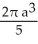 cubic units
cubic units
A)
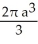 cubic units
cubic unitsB)
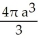 cubic units
cubic unitsC)
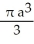 cubic units
cubic unitsD)
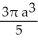 cubic units
cubic unitsE)
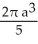 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
16
Find the volume of the solid generated when the region lying under the curve y = 4 - x2 and above the x-axis is rotated about the line y = -1.
A)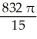 cubic units
cubic units
B)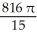 cubic units
cubic units
C)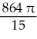 cubic units
cubic units
D)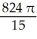 cubic units
cubic units
E)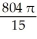 cubic units
cubic units
A)
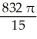 cubic units
cubic unitsB)
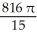 cubic units
cubic unitsC)
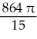 cubic units
cubic unitsD)
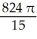 cubic units
cubic unitsE)
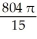 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
17
A cylindrical hole of radius r cm is drilled through the centre of a ball of radius R cm (where R > r). Find the volume of the remaining part of the ball.
A)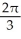
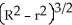
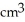
B)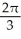
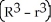
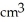
C)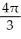
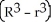
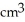
D)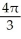
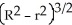
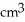
E)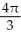
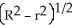
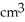
A)
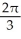
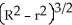
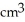
B)
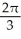
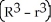
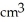
C)
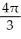
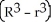
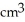
D)
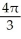
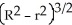
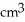
E)
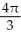
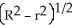
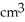

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
18
Find the volume of a solid formed by revolving the disk bounded by a circle of radius a cm about a line tangent to that circle.
A) 2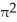
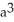
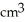
B)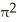
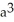
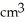
C)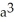
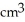
D) 4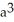
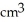
E) 4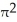
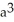
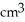
A) 2
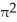
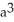
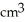
B)
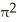
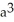
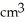
C)
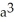
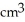
D) 4
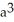
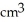
E) 4
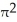
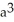
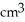

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
19
The plane region bounded by the curve 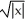 +
+ 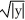 = 1 is revolved about the line x = 2. Find the volume of the solid generated.
= 1 is revolved about the line x = 2. Find the volume of the solid generated.
A)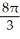 cubic units
cubic units
B)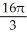 cubic units
cubic units
C)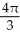 cubic units
cubic units
D)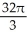 cubic units
cubic units
E)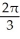 cubic units
cubic units
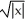 +
+ 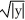 = 1 is revolved about the line x = 2. Find the volume of the solid generated.
= 1 is revolved about the line x = 2. Find the volume of the solid generated.A)
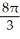 cubic units
cubic unitsB)
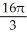 cubic units
cubic unitsC)
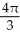 cubic units
cubic unitsD)
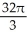 cubic units
cubic unitsE)
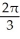 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
20
For what real values of the constant k does the region lying under the curve y = 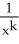 above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
A) < k 1
< k 1
B) < k < 1
< k < 1
C) < k <
< k <
D) 0 < k <
E) 0 < k 1
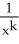 above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?
above the x-axis and to the right of the line x = 1 have infinite area but gives rise to a solid with finite volume when rotated about the x-axis?A)
 < k 1
< k 1B)
 < k < 1
< k < 1C)
 < k <
< k < D) 0 < k <

E) 0 < k 1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
21
Find the volume of the solid generated by revolving the plane region bounded by the graphs of 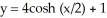 and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.
and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.
A) 27 cubic units
B)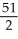 cubic units
cubic units
C) 21 cubic units
D) 37 cubic units
E) 45 cubic units
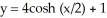 and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.
and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.A) 27 cubic units
B)
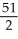 cubic units
cubic unitsC) 21 cubic units
D) 37 cubic units
E) 45 cubic units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
22
If R is the region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b (as shown in the figure below), then the volume V of the solid generated by revolving the region R about the line x = -2 is V = 2 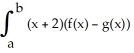 dx.
dx.
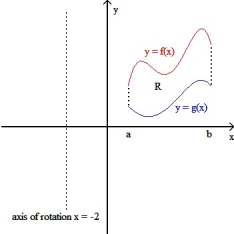
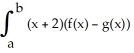 dx.
dx.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
23
The solid generated by revolving the plane region R about the x-axis has the same volume as the solid generated by revolving the region R about the y-axis.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
24
Let R be the plane region enclosed by the graphs of y = f(x) and y = g(x) from x = a to x = b , where a > 0(as shown in the figure below).If the solid generated by revolving the plane region R about the x-axis has the same volume as the solid generated by revolving the region R about the y-axis , then f and g satisfy which equation for all x > 0?
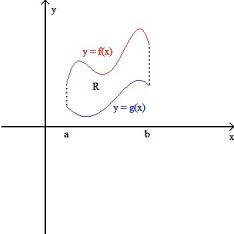
A) f(x) = - g(x)
B) f(x) + g(x) = x
C) f(x) + g(x) =
D) f(x) + g(x) = 2x
E) f(x) + g(x) = (x -2)

A) f(x) = - g(x)
B) f(x) + g(x) = x
C) f(x) + g(x) =

D) f(x) + g(x) = 2x
E) f(x) + g(x) = (x -2)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
25
Find the volume of the solid generated by revolving the region enclosed by the graphs of y = 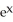 and the x-axis from x = 0 to x = 1 about the y-axis.
and the x-axis from x = 0 to x = 1 about the y-axis.
A) 2 (2e -1)
B) 2
C) e
D)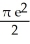
E)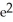
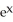 and the x-axis from x = 0 to x = 1 about the y-axis.
and the x-axis from x = 0 to x = 1 about the y-axis.A) 2 (2e -1)
B) 2
C) e
D)
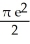
E)
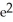

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the volume of a right circular cone of base radius r and height h.
A)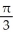
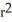 h cubic units
h cubic units
B)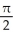
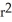 h cubic units
h cubic units
C)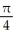
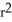 h cubic units
h cubic units
D)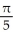
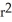 h cubic units
h cubic units
E)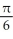
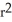 h cubic units
h cubic units
A)
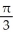
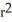 h cubic units
h cubic unitsB)
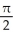
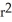 h cubic units
h cubic unitsC)
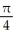
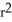 h cubic units
h cubic unitsD)
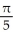
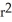 h cubic units
h cubic unitsE)
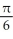
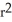 h cubic units
h cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
27
Find the volume of an elliptical cone whose base in the horizontal xy-plane is the elliptic disk 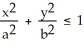 (where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.
(where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.
A)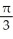 abh cubic units
abh cubic units
B)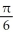 abh cubic units
abh cubic units
C)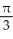
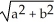 h cubic units
h cubic units
D)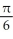
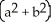 h cubic units
h cubic units
E)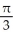
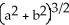 h cubic units
h cubic units
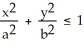 (where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.
(where a > 0 and b > 0) and whose vertex is at height h directly above the centre of the base.A)
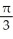 abh cubic units
abh cubic unitsB)
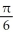 abh cubic units
abh cubic unitsC)
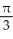
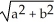 h cubic units
h cubic unitsD)
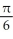
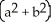 h cubic units
h cubic unitsE)
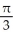
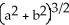 h cubic units
h cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
28
A pyramid has a triangular base of area A and has a height of h measured perpendicular to the plane of the base. Determine the volume of the pyramid.
A) Ah cubic units
Ah cubic units
B) Ah cubic units
C) Ah cubic units
Ah cubic units
D) Ah cubic units
Ah cubic units
E) Ah cubic units
A)
 Ah cubic units
Ah cubic unitsB) Ah cubic units
C)
 Ah cubic units
Ah cubic unitsD)
 Ah cubic units
Ah cubic unitsE) Ah cubic units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
29
A cube has edge length a cm and one corner at position O. A plane passing through the three corners of the cube that are adjacent to corner O slices the cube into two pieces. Find the volume of the smaller piece.
A)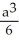
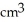
B)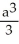
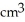
C)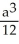
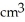
D)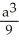
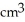
E)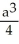
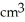
A)
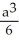
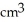
B)
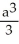
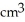
C)
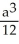
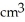
D)
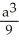
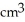
E)
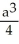

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the volume of a solid whose base is the region in the first quadrant bounded by the line  and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.
and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.
A)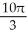 cubic units
cubic units
B)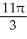 cubic units
cubic units
C) 4 cubic units
D)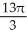 cubic units
cubic units
E)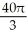 cubic units
cubic units
 and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.
and the coordinate axes if every planar section perpendicular to the x-axis is a semicircle.A)
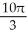 cubic units
cubic unitsB)
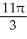 cubic units
cubic unitsC) 4 cubic units
D)
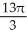 cubic units
cubic unitsE)
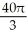 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
31
The base of a certain solid is a circular disk of radius a cm. Cross-sections of the solid in planes perpendicular to a specific diameter of the base are equilateral triangles. Find the volume of the solid.
A)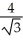
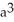
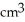
B)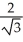
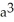
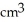
C) 2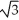
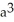
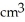
D)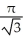
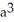
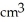
E) 4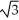
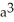
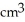
A)
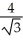
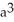
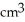
B)
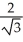
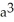
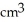
C) 2
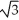
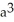
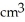
D)
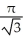
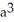
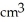
E) 4
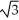
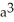
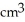

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
32
A ball of radius r has volume V(r) = 
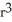 cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
A) S(r) = 4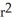 square units
square units
B) S(r) = 8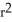 square units
square units
C) S(r) = 2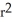 square units
square units
D) S(r) = 8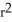 square units
square units
E) S(r) =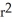 square units
square units

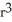 cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.A) S(r) = 4
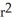 square units
square unitsB) S(r) = 8
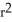 square units
square unitsC) S(r) = 2
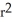 square units
square unitsD) S(r) = 8
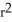 square units
square unitsE) S(r) =
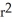 square units
square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
33
A certain solid S has a horizontal plane region R as its base and has height h cm measured perpendicular to R. For 0 < z < h, the volume of that part of S lying beneath the plane at height z cm above R is V(z) = 2z + z3 cm3. Find (a) the area of the cross-section of S in the plane at height z cm and (b) the area of R.
A) (a) 2 + 3z2 cm2, (b) 2 cm2
B) (a) 1 + 3z2 cm2, (b) 1 cm2
C) (a) 3 + z2 cm2, (b) 3 cm2
D) (a) 2 + 4z2 cm2, (b) 3 cm2
E) (a) 1 + 2z2 cm2, (b) 1 cm2
A) (a) 2 + 3z2 cm2, (b) 2 cm2
B) (a) 1 + 3z2 cm2, (b) 1 cm2
C) (a) 3 + z2 cm2, (b) 3 cm2
D) (a) 2 + 4z2 cm2, (b) 3 cm2
E) (a) 1 + 2z2 cm2, (b) 1 cm2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
34
A notch is cut out of a vertical cylindrical log of radius r cm by two planar saw cuts that meet along a horizontal line passing through the centre of the log. If the saw cuts make angles ± 30º with the horizontal (so that the angle of the notch is 60º), find the volume of wood cut out of the log in making the notch.
A)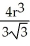 cm 3
cm 3
B)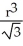 cm3
cm3
C)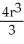 cm3
cm3
D)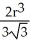 cm3
cm3
E)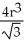 cm3
cm3
A)
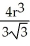 cm 3
cm 3B)
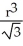 cm3
cm3C)
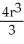 cm3
cm3D)
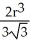 cm3
cm3E)
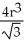 cm3
cm3
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
35
Let A(x) be the cross-sectional area of a solid by planes perpendicular to the x-axis. If the volume of the solid that lies between x = 1 and x = z > 1 is V = 4 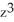 + 2, find A(x).
+ 2, find A(x).
A) 12 square units
B)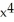 + 2x - 3 square units
+ 2x - 3 square units
C) 12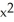 square units
square units
D)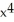 + 2x + C square units
+ 2x + C square units
E) 6 square units
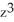 + 2, find A(x).
+ 2, find A(x).A) 12 square units
B)
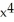 + 2x - 3 square units
+ 2x - 3 square unitsC) 12
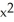 square units
square unitsD)
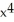 + 2x + C square units
+ 2x + C square unitsE) 6 square units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
36
Find the total length of the hypocycloid 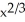 +
+ 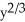 =
= 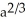 .
.
A) 12a units
B) 10a units
C) 8a units
D) 6a units
E) a units
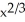 +
+ 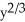 =
= 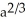 .
.A) 12a units
B) 10a units
C) 8a units
D) 6a units
E) a units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find the length of the arc y = ln 
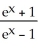
 between x = 1 and x = 2.
between x = 1 and x = 2.
A) ln(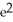 + 2) - 1 units
+ 2) - 1 units
B) ln(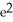 + 1) - 2 units
+ 1) - 2 units
C) ln(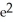 - 1) - 1 units
- 1) - 1 units
D) ln(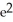 + 1) - 1 units
+ 1) - 1 units
E) ln(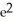 - 1) + 1 units
- 1) + 1 units

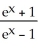
 between x = 1 and x = 2.
between x = 1 and x = 2.A) ln(
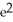 + 2) - 1 units
+ 2) - 1 unitsB) ln(
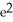 + 1) - 2 units
+ 1) - 2 unitsC) ln(
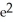 - 1) - 1 units
- 1) - 1 unitsD) ln(
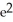 + 1) - 1 units
+ 1) - 1 unitsE) ln(
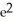 - 1) + 1 units
- 1) + 1 units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
38
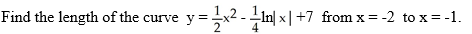
A)
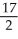 - ln(2)
- ln(2)B)
 -
-  ln(2)
ln(2)C)
 +
+  ln(2)
ln(2)D)
 ln(2) -
ln(2) - 
E)
 -
-  ln(32)
ln(32)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
39
Find the length of the arc y = ln(sec x) between x = 0 and x = 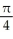 .
.
A) ln(2 +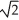 ) units
) units
B) ln(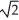 - 1) units
- 1) units
C) ln(1 +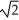 ) units
) units
D) ln(2 -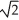 ) units
) units
E) ln(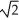 ) units
) units
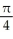 .
.A) ln(2 +
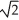 ) units
) unitsB) ln(
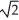 - 1) units
- 1) unitsC) ln(1 +
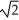 ) units
) unitsD) ln(2 -
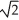 ) units
) unitsE) ln(
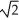 ) units
) units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
40
Find the arc length of the curve x = 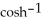 (y) from y =
(y) from y =  to y =
to y =  .
.
A)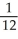
B)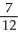
C)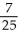
D)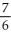
E)
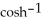 (y) from y =
(y) from y =  to y =
to y =  .
.A)
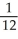
B)
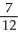
C)
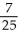
D)
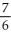
E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
41
Find the area of the surface obtained by rotating the curve y = 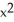 , -1 x 1, about the y-axis.
, -1 x 1, about the y-axis.
A)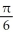 (5
(5 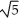 - 1) square units
- 1) square units
B)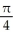 (5
(5 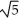 + 1) square units
+ 1) square units
C)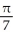 (5
(5 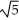 - 1) square units
- 1) square units
D)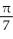 (5
(5 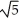 + 1) square units
+ 1) square units
E)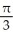 (5
(5 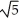 - 1) square units
- 1) square units
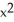 , -1 x 1, about the y-axis.
, -1 x 1, about the y-axis.A)
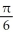 (5
(5 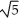 - 1) square units
- 1) square unitsB)
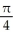 (5
(5 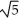 + 1) square units
+ 1) square unitsC)
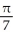 (5
(5 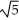 - 1) square units
- 1) square unitsD)
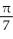 (5
(5 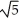 + 1) square units
+ 1) square unitsE)
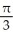 (5
(5 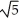 - 1) square units
- 1) square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find the area of the surface obtained by rotating the curve y = 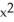 , -1 x 1, about the x-axis.
, -1 x 1, about the x-axis.
A)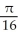
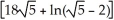 square units
square units
B)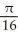
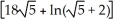 square units
square units
C)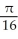
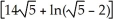 square units
square units
D)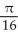
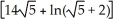 square units
square units
E)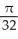
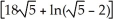 square units
square units
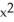 , -1 x 1, about the x-axis.
, -1 x 1, about the x-axis.A)
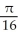
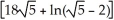 square units
square unitsB)
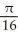
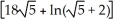 square units
square unitsC)
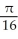
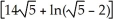 square units
square unitsD)
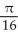
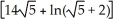 square units
square unitsE)
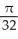
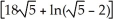 square units
square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the area of the surface generated by rotating 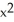 +
+ 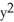 =
= 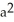 about y = a.
about y = a.
A) 6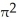
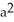 square units
square units
B) 8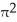
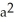 square units
square units
C) 2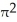
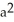 square units
square units
D) 4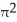
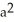 square units
square units
E)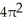
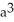 square units
square units
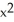 +
+ 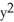 =
= 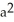 about y = a.
about y = a.A) 6
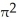
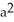 square units
square unitsB) 8
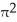
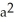 square units
square unitsC) 2
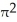
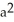 square units
square unitsD) 4
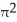
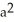 square units
square unitsE)
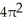
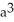 square units
square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
44
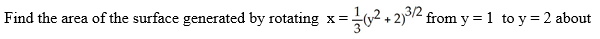 the x-axis.
the x-axis.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the area of the surface generated by rotating y = 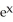 , - x 0 about y = 0.
, - x 0 about y = 0.
A)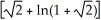 square units
square units
B)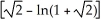 square units
square units
C)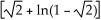 square units
square units
D)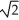 + ln(1 +
+ ln(1 + 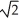 ) square units
) square units
E)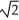 - ln(1 +
- ln(1 + 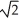 ) square units
) square units
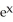 , - x 0 about y = 0.
, - x 0 about y = 0.A)
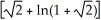 square units
square unitsB)
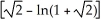 square units
square unitsC)
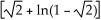 square units
square unitsD)
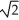 + ln(1 +
+ ln(1 + 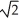 ) square units
) square unitsE)
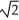 - ln(1 +
- ln(1 + 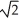 ) square units
) square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find the area of the oval surface obtained by rotating the ellipse 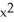 + 4
+ 4 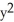 = 1 about its major axis (i.e., about the x-axis).
= 1 about its major axis (i.e., about the x-axis).
A)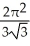 -
- 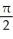 square units
square units
B)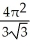 -
- 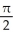 square units
square units
C)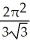 +
+ 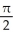 square units
square units
D)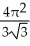 +
+ 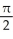 square units
square units
E)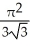 -
- 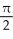 square units
square units
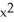 + 4
+ 4 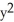 = 1 about its major axis (i.e., about the x-axis).
= 1 about its major axis (i.e., about the x-axis).A)
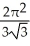 -
- 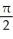 square units
square unitsB)
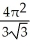 -
- 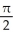 square units
square unitsC)
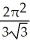 +
+ 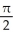 square units
square unitsD)
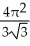 +
+ 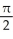 square units
square unitsE)
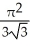 -
- 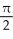 square units
square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find the length of the curve y = 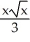 -
- 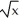 from x = 0 to x = 3.
from x = 0 to x = 3.
A) 2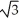 units
units
B)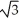 units
units
C) 3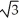 units
units
D) 4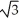 units
units
E) 5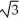 units
units
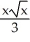 -
- 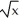 from x = 0 to x = 3.
from x = 0 to x = 3.A) 2
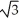 units
unitsB)
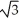 units
unitsC) 3
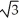 units
unitsD) 4
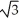 units
unitsE) 5
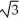 units
units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find the area of the surface generated by rotating y = ![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f4_e8b0_a0f8_d16a73ccaffa_TB9661_11.jpg) -
- ![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f4_e8b1_a0f8_ddaef5c36335_TB9661_11.jpg) where x
where x ![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 3] about y = 0.
[0, 3] about y = 0.
A) 3 square units
B) 4 square units
C) 2 square units
D) 6 square units
E) square units
![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f4_e8b0_a0f8_d16a73ccaffa_TB9661_11.jpg) -
- ![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f4_e8b1_a0f8_ddaef5c36335_TB9661_11.jpg) where x
where x ![<strong>Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.</strong> A) 3 \pi square units B) 4 \pi square units C) 2 \pi square units D) 6 \pi square units E) \pi square units](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 3] about y = 0.
[0, 3] about y = 0.A) 3 square units
B) 4 square units
C) 2 square units
D) 6 square units
E) square units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find, correct to 4 decimal places, the length of the curve y = 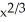 from x = 1 to x = 8.
from x = 1 to x = 8.
A) 19.1981 units
B) 14.6572 units
C) 3.4123 units
D) 7.6337 units
E) 22.8030 units
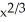 from x = 1 to x = 8.
from x = 1 to x = 8.A) 19.1981 units
B) 14.6572 units
C) 3.4123 units
D) 7.6337 units
E) 22.8030 units

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find the length of the closed loop part of the curve 3 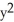 = x
= x 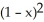 .
.
A)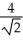 units
units
B)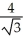 units
units
C)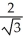 units
units
D) 2 units
E) 1 unit
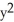 = x
= x 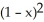 .
.A)
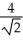 units
unitsB)
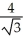 units
unitsC)
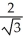 units
unitsD) 2 units
E) 1 unit

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
51
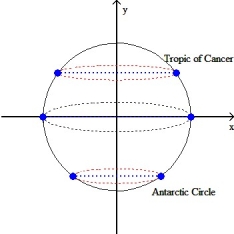
Assuming the Earth is spherical with radius 6378 km, find the area of the surface of the Earth between the Tropic of Cancer (23.5° north latitude) and the Antarctic Circle (66.5° south latitude) as shown in the figure below.


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
52
Find the centre of mass of the semicircular plate 0 y 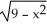 assuming it has constant density.
assuming it has constant density.
A)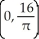
B)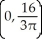
C)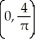
D)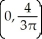
E)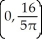
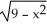 assuming it has constant density.
assuming it has constant density.A)
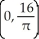
B)
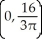
C)
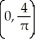
D)
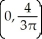
E)
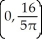

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
53
Find the centre of mass of a system of point masses m1 = 6, m2 = 3, m3 = 2, and m4 = 9 located at (3, -2), (0, 0), (-5, 3), and (4, 2), respectively.
A)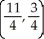
B)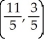
C)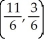
D)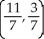
E)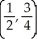
A)
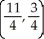
B)
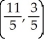
C)
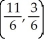
D)
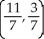
E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
54
A conical tank with vertex at the bottom and top radius 10 cm is 40 cm tall. It is filled with a substance whose density at depth y cm is (2 + y) g/ 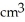 . Find the total mass of the substance filling the tank.
. Find the total mass of the substance filling the tank.
A) 15 kg
B) 16 kg
C) 17 kg
D) 18 kg
E) none of the above
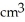 . Find the total mass of the substance filling the tank.
. Find the total mass of the substance filling the tank.A) 15 kg
B) 16 kg
C) 17 kg
D) 18 kg
E) none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
55
A triangular plate has vertices at (0, 0), (a, 0), and (0,b), where a > 0 and b > 0. The plate has variable thickness; at position (x, y) its thickness is 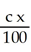 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
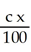 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
56
A triangular plate has vertices at (0, 0), (a, 0), and (0, b), where a > 0 and b > 0. The plate has variable thickness; at position (x, y) its thickness is 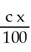 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
A)
B)
C)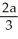
D)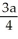
E)
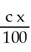 . Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.
. Assuming the plate is made of material of constant density, find the x-coordinate of its centre of mass.A)

B)

C)
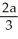
D)
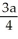
E)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
57
Consider the finite plane region bounded by the coordinate axes and the line 4x + 3y = 12. Assuming the region has constant areal density 1, find the moments of this region about the coordinate axes.
A)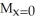 = 8,
= 8, 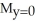 = 6
= 6
B)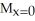 = 6,
= 6, 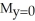 = 8
= 8
C)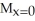 = 6,
= 6, 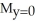 = 6
= 6
D)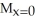 = 8,
= 8, 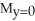 = 8
= 8
E)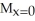 = 6,
= 6, 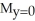 = 0
= 0
A)
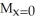 = 8,
= 8, 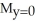 = 6
= 6B)
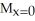 = 6,
= 6, 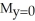 = 8
= 8C)
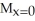 = 6,
= 6, 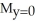 = 6
= 6D)
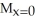 = 8,
= 8, 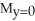 = 8
= 8E)
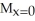 = 6,
= 6, 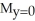 = 0
= 0
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
58
Find the mass of a thin plate that occupies the planar region described by 0 y sin(2x), 0 x 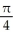 if the areal density is given by
if the areal density is given by 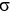 (x) = 8x.
(x) = 8x.
A) 32
B) 2
C) 4
D)
E) 0
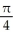 if the areal density is given by
if the areal density is given by 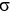 (x) = 8x.
(x) = 8x.A) 32
B) 2
C) 4
D)
E) 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find the moment about the x-axis of a plate of constant areal density 1 occupying the finite plane region bounded by the x-axis and the curve y = -16 + 10x - 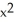 .
.
A)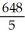
B)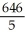
C)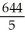
D)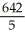
E)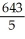
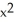 .
.A)
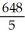
B)
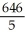
C)
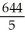
D)
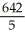
E)
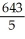

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
60
Find the moment about the line x = 4 of a plate of constant density 1 occupying the finite plane region bounded by the x-axis and the curve y = -16 + 10x - x2.
A) 32
B) 36
C) 34
D) 38
E) 30
A) 32
B) 36
C) 34
D) 38
E) 30

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find the moment about the x-axis of a thin plate that occupies the planar region described by 0 y 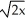 , 0 x 1 if the areal density is given by
, 0 x 1 if the areal density is given by 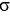 (x) = ex.
(x) = ex.
A)
B) 1
C)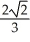 e
e
D) 2e - 1
E) e - 1
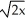 , 0 x 1 if the areal density is given by
, 0 x 1 if the areal density is given by 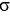 (x) = ex.
(x) = ex.A)

B) 1
C)
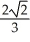 e
eD) 2e - 1
E) e - 1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
62
A thin plate occupying the planar region 0 x g(y), c y d has mass equal to 2 units. If the areal density 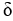 (y) =
(y) = 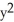 ,
, 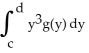 = 6, and
= 6, and 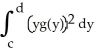 = 16, then the centre of mass of the plate is at the point:
= 16, then the centre of mass of the plate is at the point:
A) ( ,
,  ) = (16, 12)
) = (16, 12)
B) ( ,
,  ) = (12, 16)
) = (12, 16)
C) ( ,
,  ) = (4, 3)
) = (4, 3)
D) ( ,
,  ) = (0, 0)
) = (0, 0)
E) ( ,
,  ) = (3, 4)
) = (3, 4)
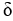 (y) =
(y) = 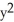 ,
, 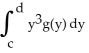 = 6, and
= 6, and 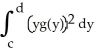 = 16, then the centre of mass of the plate is at the point:
= 16, then the centre of mass of the plate is at the point:A) (
 ,
,  ) = (16, 12)
) = (16, 12)B) (
 ,
,  ) = (12, 16)
) = (12, 16)C) (
 ,
,  ) = (4, 3)
) = (4, 3)D) (
 ,
,  ) = (0, 0)
) = (0, 0)E) (
 ,
,  ) = (3, 4)
) = (3, 4)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
63
Find the moment about the x-axis of the region in the first quadrant bounded by the lines y = 5x, y = 3x, x = 3. Assume the areal density is 1.
A) 16
B) 18
C) 17
D) 20
E) 14
A) 16
B) 18
C) 17
D) 20
E) 14

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
64
A hemispherical bowl of radius r cm is filled with water. How far below the surface is the centre of mass of this water?
A)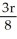 cm
cm
B)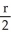 cm
cm
C)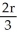 cm
cm
D) cm
cm
E) cm
cm
A)
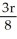 cm
cmB)
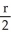 cm
cmC)
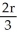 cm
cmD)
 cm
cmE)
 cm
cm
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
65
The plane region defined by 0 ≤ y ≤ 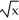 , 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
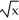 , 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 ≤ x ≤ a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
66
The plane region defined by 0 y 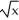 , 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
A) on the x-axis,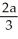 units to the right of the origin
units to the right of the origin
B) on the x-axis,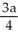 units to the right of the origin
units to the right of the origin
C) on the x-axis, units to the right of the origin
units to the right of the origin
D) on the x-axis,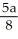 units to the right of the origin
units to the right of the origin
E) on the x-axis,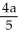 units to the right of the origin
units to the right of the origin
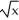 , 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?
, 0 x a is revolved about the x-axis to generate a 3-dimensional region that is filled with material of constant density. Where is the centre of mass of this material?A) on the x-axis,
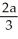 units to the right of the origin
units to the right of the originB) on the x-axis,
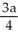 units to the right of the origin
units to the right of the originC) on the x-axis,
 units to the right of the origin
units to the right of the originD) on the x-axis,
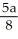 units to the right of the origin
units to the right of the originE) on the x-axis,
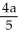 units to the right of the origin
units to the right of the origin
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
67
Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9b_a0f8_19a5a84c4321_TB9661_11.jpg) ].
].
A)![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9c_a0f8_9f9488ea10bd_TB9661_11.jpg)
B)![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9d_a0f8_355b2714f734_TB9661_11.jpg)
C)![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9e_a0f8_494518fc8c61_TB9661_11.jpg)
D)![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9f_a0f8_739fde175653_TB9661_11.jpg)
E)![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6fa0_a0f8_e9ad9e557b61_TB9661_11.jpg)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9b_a0f8_19a5a84c4321_TB9661_11.jpg) ].
].A)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9c_a0f8_9f9488ea10bd_TB9661_11.jpg)
B)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9d_a0f8_355b2714f734_TB9661_11.jpg)
C)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9e_a0f8_494518fc8c61_TB9661_11.jpg)
D)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6f9f_a0f8_739fde175653_TB9661_11.jpg)
E)
![<strong>Determine the centre of mass for the region bounded by y = 2 sin 2x, y = 0 on the interval [0, ].</strong> A) B) C) D) E)](https://d2lvgg3v3hfg70.cloudfront.net/TB9661/11ee77e1_77f6_6fa0_a0f8_e9ad9e557b61_TB9661_11.jpg)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
68
Find the centroid of the region in the first quadrant bounded by the lines y = 5x, y = x, and x = 4.
A)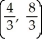
B)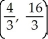
C)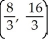
D)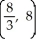
E)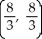
A)
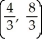
B)
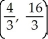
C)
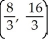
D)
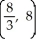
E)
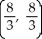

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
69
Determine the centroid of the finite plane region bounded by y = x3 and y = 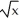 .
.
A)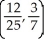
B)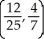
C)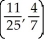
D)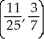
E)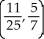
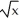 .
.A)
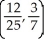
B)
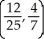
C)
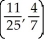
D)
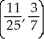
E)
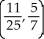

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
70
Find the centroid of the region bounded by the x-axis and the curve y = -16 + 10 x - x2.
A)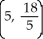
B)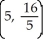
C)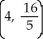
D)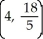
E)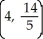
A)
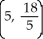
B)
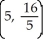
C)
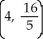
D)
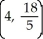
E)
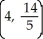

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find the volume of the solid ring obtained by rotating the disc x2 + 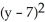 = 9 about the x-axis.
= 9 about the x-axis.
A) 126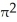 cubic units
cubic units
B) 144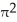 cubic units
cubic units
C) 112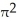 cubic units
cubic units
D) 169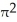 cubic units
cubic units
E) 196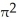 cubic units
cubic units
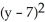 = 9 about the x-axis.
= 9 about the x-axis.A) 126
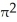 cubic units
cubic unitsB) 144
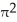 cubic units
cubic unitsC) 112
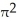 cubic units
cubic unitsD) 169
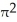 cubic units
cubic unitsE) 196
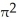 cubic units
cubic units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find the centroid of the planar region bounded by y =  , y = 0, x = 1, and x = 2.
, y = 0, x = 1, and x = 2.
A)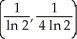
B)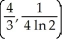
C)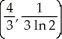
D)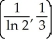
E)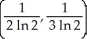
 , y = 0, x = 1, and x = 2.
, y = 0, x = 1, and x = 2.A)
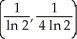
B)
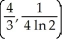
C)
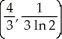
D)
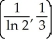
E)
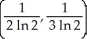

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
73
Find the coordinates of the centroid of the region enclosed by y = sin(x) and the x-axis from x = 0 to 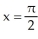 .
.
A)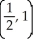
B)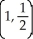
C)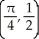
D)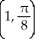
E)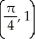
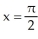 .
.A)
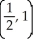
B)
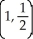
C)
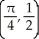
D)
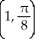
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
74
Find the centroid of the finite plane region bounded by the curve y = 4 - x2 and the liney = x + 2.
A)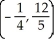
B)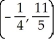
C)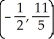
D)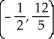
E)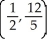
A)
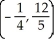
B)
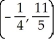
C)
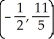
D)
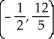
E)
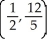

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find the centroid of the finite plane region bounded by y = x2 and y = x.
A)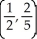
B)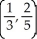
C)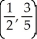
D)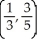
E)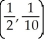
A)
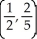
B)
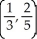
C)
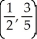
D)

E)
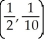

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
76
A finite region R is contained in the first quadrant of the xy-plane. The centroid of R is the point (3, h). When R is revolved about the y-axis it generates a solid having volume 12 cubic units. When R is revolved about the x-axis it generates a solid having volume 32 cubic units. Find (a) the area of R and (b) the value of h.
A) (a)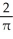 square units, (b) 8
square units, (b) 8
B) (a) 2 square units, (b)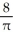
C) (a)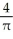 square units, (b) 4
square units, (b) 4
D) (a) 4 square units, (b)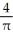
E) (a)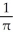 square units, (b) 4
square units, (b) 4
A) (a)
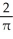 square units, (b) 8
square units, (b) 8B) (a) 2 square units, (b)
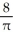
C) (a)
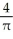 square units, (b) 4
square units, (b) 4D) (a) 4 square units, (b)
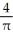
E) (a)
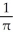 square units, (b) 4
square units, (b) 4
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
77
Find the centroid of the finite plane region bounded by y = 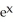 , y =
, y = 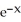 , and x = 1.
, and x = 1.
A)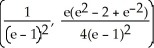
B)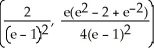
C)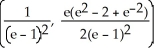
D)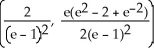
E)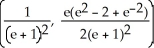
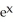 , y =
, y = 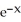 , and x = 1.
, and x = 1.A)
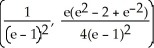
B)
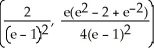
C)
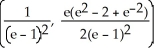
D)
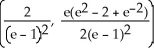
E)
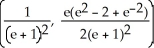

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
78
A triangle T has vertices ( 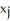 ,
,  ), j = 1, 2, 3 (where each
), j = 1, 2, 3 (where each 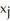 > 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?
> 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?
A)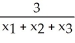 square units
square units
B)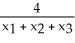 square units
square units
C)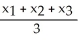 square units
square units
D)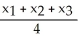 square units
square units
E)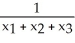 square units
square units
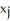 ,
,  ), j = 1, 2, 3 (where each
), j = 1, 2, 3 (where each 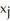 > 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?
> 0). If the volume of the solid of revolution obtained by revolving T about the y-axis is 2 cubic units, what is the area of T?A)
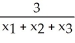 square units
square unitsB)
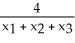 square units
square unitsC)
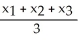 square units
square unitsD)
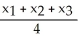 square units
square unitsE)
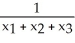 square units
square units
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
79
Use Pappus's Theorem to find the volume of the solid of revolution obtained by rotating the triangular plane region specified by 0 y 1 -  about (a) the line x = 2 and(b) the line y = 2.
about (a) the line x = 2 and(b) the line y = 2.
A) (a) 4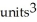 , (b)
, (b) 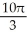
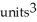
B) (a) 2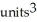 , (b)
, (b) 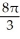
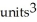
C) (a) 4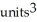 , (b)
, (b) 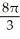
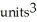
D) (a) 2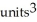 , (b)
, (b) 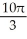
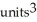
E) (a) 2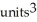 , (b)
, (b) 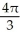
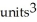
 about (a) the line x = 2 and(b) the line y = 2.
about (a) the line x = 2 and(b) the line y = 2.A) (a) 4
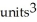 , (b)
, (b) 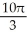
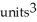
B) (a) 2
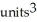 , (b)
, (b) 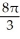
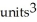
C) (a) 4
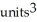 , (b)
, (b) 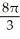
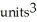
D) (a) 2
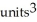 , (b)
, (b) 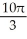
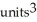
E) (a) 2
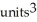 , (b)
, (b) 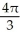

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck
80
Use Pappus's Theorem to find the volume of the solid generated by revolving the region R enclosed by y = 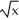 , x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(
, x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(  ,
,  ) = (
) = ( 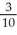 ,
,  ).
).
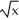 , x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(
, x = 0, and y =1 about the line y = -1 given that the centroid of the region R is at the point(  ,
,  ) = (
) = ( 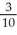 ,
,  ).
).
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 139 في هذه المجموعة.
فتح الحزمة
k this deck








