Deck 3: Linear Programming Modeling Applications with Computer Analyses in Excel
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/49
العب
ملء الشاشة (f)
Deck 3: Linear Programming Modeling Applications with Computer Analyses in Excel
1
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.
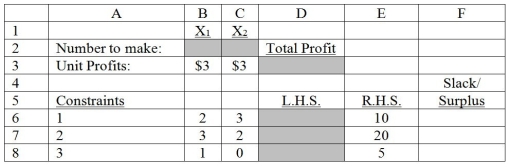
-Refer to the spreadsheet above.Which cell(s)specifies the "changing cells" in Solver?
A)B1:C1
B)D6:D8
C)B3:C3
D)D3
E)B2:C2
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which cell(s)specifies the "changing cells" in Solver?
A)B1:C1
B)D6:D8
C)B3:C3
D)D3
E)B2:C2
B2:C2
2
In a multi-period production scheduling application,the decision choices in later periods are directly dependent on the decision made in earlier periods.
False
3
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which cell(s)designates the objective function as specified in "Solver"?
A)E4
B)D3
C)D2
D)B1:C1
E)B2:C2
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which cell(s)designates the objective function as specified in "Solver"?
A)E4
B)D3
C)D2
D)B1:C1
E)B2:C2
D3
4
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell F6 to compute the unused resources of constraint #1?
A)B2 - E6
B)D6 - E6
C)E6 - D6
D)E6 - B2
E)F6 - E6
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell F6 to compute the unused resources of constraint #1?
A)B2 - E6
B)D6 - E6
C)E6 - D6
D)E6 - B2
E)F6 - E6

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
5
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.What formula should be entered in cell D3 to compute total profitability?
A)=SUMPRODUCT(B1:C1,B3:C3)
B)=SUM(B3:C3)
C)=B2*B3 + C2*C3
D)=SUMPRODUCT(B3:C3,E6:E8)
E)=B1*B3 + C1*C3
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.What formula should be entered in cell D3 to compute total profitability?
A)=SUMPRODUCT(B1:C1,B3:C3)
B)=SUM(B3:C3)
C)=B2*B3 + C2*C3
D)=SUMPRODUCT(B3:C3,E6:E8)
E)=B1*B3 + C1*C3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
6
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell F8 to compute the amount by which the minimal requirement of constraint #3 has been exceeded?
A)=SUMPRODUCT(B2:C2,D3:E3)
B)D8 - E8
C)E8 - D8
D)F8 - E8
E)E8 - F8
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell F8 to compute the amount by which the minimal requirement of constraint #3 has been exceeded?
A)=SUMPRODUCT(B2:C2,D3:E3)
B)D8 - E8
C)E8 - D8
D)F8 - E8
E)E8 - F8

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
7
The media selection problem can have which of the following objectives?
A)maximizing audience exposure
B)minimizing advertising costs
C)maximizing profit
D)A and B only
E)A,B,and C
A)maximizing audience exposure
B)minimizing advertising costs
C)maximizing profit
D)A and B only
E)A,B,and C

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
8
Consider the following constraint: X₂ ≤ 30.This implies that at least 30 units of product X₂ can be produced.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
9
A company produces two products,X₁,and X₂.The constraint that illustrates the consumption of a given resource in making the two products is given by: 2X₁+3X₂ ≤ 10.This relationship implies that each unit of X1 consumes 3 units of that resource.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
10
The objective function of a transportation problem is to:
A)maximize transportation cost
B)maximize supply quantities
C)minimize total demand
D)minimize total shipping cost
E)minimize production cost
A)maximize transportation cost
B)maximize supply quantities
C)minimize total demand
D)minimize total shipping cost
E)minimize production cost

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
11
The marketing research problem has which of the following objectives?
A)maximizing audience exposure
B)minimizing advertising costs
C)minimizing interview costs
D)maximizing profit
E)minimizing the total number surveyed
A)maximizing audience exposure
B)minimizing advertising costs
C)minimizing interview costs
D)maximizing profit
E)minimizing the total number surveyed

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
12
In a multi-period production scheduling application,which equation describes the relationship between demand,production,and inventory?
A)productiont + demandₜ - inventoryₜ₋₁ = inventoryₜ
B)productiont + demandₜ + inventoryₜ₋₁ = inventoryₜ
C)productiont - demandₜ₋₁ + inventoryₜ₋₁ = inventoryₜ
D)productiont - demandₜ + inventoryₜ = inventoryₜ₋₁
E)productiont - demandₜ + inventoryₜ₋₁ = inventoryₜ
A)productiont + demandₜ - inventoryₜ₋₁ = inventoryₜ
B)productiont + demandₜ + inventoryₜ₋₁ = inventoryₜ
C)productiont - demandₜ₋₁ + inventoryₜ₋₁ = inventoryₜ
D)productiont - demandₜ + inventoryₜ = inventoryₜ₋₁
E)productiont - demandₜ + inventoryₜ₋₁ = inventoryₜ

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
13
In a multi-period production scheduling application,the decision variables typically designate:
A)the number of units to produce in a given period
B)minimizing inventory and production costs
C)the number of units held in inventory in a given period
D)the number of inventory units to produce in a given period
E)number of units to produce in a given period,along with the number of units to hold in inventory at the end of each period
A)the number of units to produce in a given period
B)minimizing inventory and production costs
C)the number of units held in inventory in a given period
D)the number of inventory units to produce in a given period
E)number of units to produce in a given period,along with the number of units to hold in inventory at the end of each period

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
14
A company produces two products,X₁,and X₂.The constraint that illustrates the consumption of a given resource in making the two products is given by: 3X₁+5X₂ ≤ 120.This relationship implies that both products can consume more than 120 units of that resource.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
15
Consider the following constraint: X₁ ≥ 40.This implies that at most 40 units of product X₁ can be produced.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
16
Which of the following statements regarding the Portfolio selection problem is False?
A)Decision variables typically involve the amount to be invested in each investment choice.
B)Minimizing risk is the most common objective.
C)Alternate formulations are possible.
D)Maximizing return on investments subject to a set of risk constraint is a typical problem formulation.
E)Legal constraints can be introduced in addition to risk constraints .
A)Decision variables typically involve the amount to be invested in each investment choice.
B)Minimizing risk is the most common objective.
C)Alternate formulations are possible.
D)Maximizing return on investments subject to a set of risk constraint is a typical problem formulation.
E)Legal constraints can be introduced in addition to risk constraints .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
17
The "Diet" problem can be classified as an "ingredient blending" linear programming application.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
18
In a multi-period production scheduling application,the objective function is to:
A)minimize production and inventory costs
B)minimize demand over the production horizon
C)maximize capacity over the production horizon
D)minimize capacity over the production horizon
E)maximize inventory
A)minimize production and inventory costs
B)minimize demand over the production horizon
C)maximize capacity over the production horizon
D)minimize capacity over the production horizon
E)maximize inventory

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
19
Which of the following statements is False regarding employee staffing applications?
A)Employee staffing problems can be formulated as assignment problems.
B)The goal of employee staffing problems is typically to determine how many employees need to start their work at the different starting times permitted.
C)The employee staffing problem is a extension of the product mix problem.
D)It is possible to have multiple optimal solutions in employee staffing applications.
E)Based on the requirements and constraints,it is possible for an employee staffing problem to become infeasible.
A)Employee staffing problems can be formulated as assignment problems.
B)The goal of employee staffing problems is typically to determine how many employees need to start their work at the different starting times permitted.
C)The employee staffing problem is a extension of the product mix problem.
D)It is possible to have multiple optimal solutions in employee staffing applications.
E)Based on the requirements and constraints,it is possible for an employee staffing problem to become infeasible.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
20
Use this information to answer the following questions.
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell D8 to compute the consumption of resource 3 (i.e. ,constraint #3)?
A)=SUMPRODUCT(B1:C1,B8:C8)
B)=SUMPRODUCT(B2:C2,B7:C7)
C)=SUMPRODUCT(B2:C2,B8:C8)
D)=SUMPRODUCT(D6:D8,E6:E8)
E)=SUMPRODUCT(B2:C2,E6:E8)
Consider the following product mix problem and its associated spreadsheet model.

-Refer to the spreadsheet above.Which equation should be entered in cell D8 to compute the consumption of resource 3 (i.e. ,constraint #3)?
A)=SUMPRODUCT(B1:C1,B8:C8)
B)=SUMPRODUCT(B2:C2,B7:C7)
C)=SUMPRODUCT(B2:C2,B8:C8)
D)=SUMPRODUCT(D6:D8,E6:E8)
E)=SUMPRODUCT(B2:C2,E6:E8)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
21
Use this information to answer the following questions.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.Assume that demand for retail outlet three (R3)increases to 300 units.How will this affect the shipping cost? Use Excel to formulate and solve this problem
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.Assume that demand for retail outlet three (R3)increases to 300 units.How will this affect the shipping cost? Use Excel to formulate and solve this problem

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
22
The objective of transportation problems is typically to either minimize total shipping costs or distances.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
23
An insurance company has three secretaries,A,B,and C,who are each capable of processing four different types of insurance claims.The amount of time required by each secretary to process a particular type of a claim is summarized in the following table.
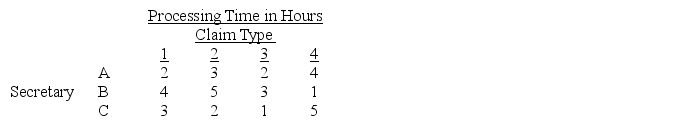
On a typical week,the insurance firm has 5 type 1 claims,4 type 2 claims,2 type 3 claims,and 3 type 4 claims.Each secretary works a maximum of 40 hours per week.The office manager wants to know how many of each type of an insurance claim should be processed by each secretary to minimize the total processing time.Use Excel to formulate and solve this problem.
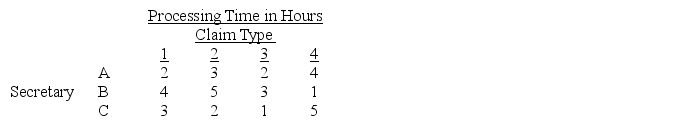
On a typical week,the insurance firm has 5 type 1 claims,4 type 2 claims,2 type 3 claims,and 3 type 4 claims.Each secretary works a maximum of 40 hours per week.The office manager wants to know how many of each type of an insurance claim should be processed by each secretary to minimize the total processing time.Use Excel to formulate and solve this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
24
Alternate optimal solutions are not common in linear programming applications.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
25
Use this information to answer the following questions.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.The company wants to come up with an optimal shipping strategy to minimize its total shipping cost.Use Excel to formulate and solve this problem.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.The company wants to come up with an optimal shipping strategy to minimize its total shipping cost.Use Excel to formulate and solve this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
26
Production,inventory,and demand are typical decision variables in a production scheduling,multi-period linear programming application.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
27
The "Transportation" problem involves determining the amount of goods to be transported from a number of origins to a number of destinations.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
28
A company wants to determine how to allocate its $200,000 advertising budget to market a new cereal.The company is considering newspaper ads,television ads,and radio ads.The following table illustrates the cost of advertising in these different media and the exposure to new customers reached by increasing the number of ads in each medium.

Use Excel to formulate and solve this problem to maximize audience exposure.

Use Excel to formulate and solve this problem to maximize audience exposure.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
29
Use this information to answer the following questions.
The following table contains information on the cost to run four jobs (1,2,3,and 4)on four available machines (A,B,C,and D).

Refer to the table above.Assume that job number 4 was canceled and will no longer be processed.How will this affect the job-machine assignment? Use Excel to model and solve this problem to determine the least costly assignment.
The following table contains information on the cost to run four jobs (1,2,3,and 4)on four available machines (A,B,C,and D).

Refer to the table above.Assume that job number 4 was canceled and will no longer be processed.How will this affect the job-machine assignment? Use Excel to model and solve this problem to determine the least costly assignment.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
30
An investment company currently has 1 million dollars available for investment in five different stocks.The company wants to maximize the interest earned over the next year.The five investment possibilities along with the expected interest earned are shown below.To manage risk,the investment firm wishes to have at least 35% of the investment in stocks A and B.Furthermore,no more than 15% of the investment may be in stock E.Model and solve this problem in Excel.
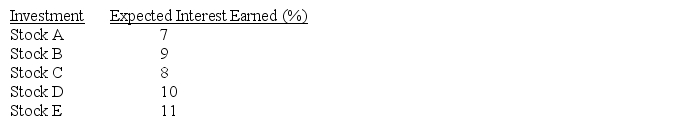
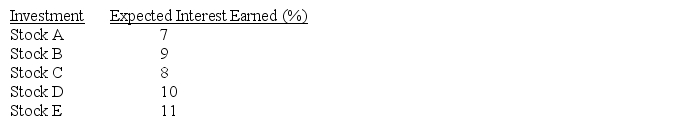

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
31
In a "Portfolio Selection" application,the objective function is always to minimize risk,given a set of legal and policy constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
32
The "Sinking Fund" problem can be classified as a multi-period linear programming application.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
33
Diet and feed mix problems are special classes of the general product mix problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
34
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.

Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.Also,there is a weekly demand of 10 units of product C each week.Use Excel to formulate and solve this problem.

Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.Also,there is a weekly demand of 10 units of product C each week.Use Excel to formulate and solve this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
35
Use this information to answer the following questions.
A beer distributor wants to prepare an aggregate plan for the next 6 weeks.Demand can be met using regular time production,overtime production,or a combination of both as illustrated below:

Refer to the table above.Assume that the beer distributor has the option of "subcontracting" beer cases to supplement the existing capacity.Subcontracting can handle a maximum of 5 cases per week.Subcontracting cost per case is $80.Also,due to an upcoming holiday season,the beer distributor wants to maintain a safety stock of at least 5 cases per week.Use Excel to formulate and solve this multiperiod production scheduling problem.
A beer distributor wants to prepare an aggregate plan for the next 6 weeks.Demand can be met using regular time production,overtime production,or a combination of both as illustrated below:

Refer to the table above.Assume that the beer distributor has the option of "subcontracting" beer cases to supplement the existing capacity.Subcontracting can handle a maximum of 5 cases per week.Subcontracting cost per case is $80.Also,due to an upcoming holiday season,the beer distributor wants to maintain a safety stock of at least 5 cases per week.Use Excel to formulate and solve this multiperiod production scheduling problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
36
The objective function of the "Diet" problem is usually to maximize the food ingredient combination to satisfy a stated nutritional requirement.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
37
Use this information to answer the following questions.
The following table contains information on the cost to run four jobs (1,2,3,and 4)on four available machines (A,B,C,and D).

Refer to the table above.Use Excel to model and solve this problem to determine the least costly job-machine assignment.
The following table contains information on the cost to run four jobs (1,2,3,and 4)on four available machines (A,B,C,and D).

Refer to the table above.Use Excel to model and solve this problem to determine the least costly job-machine assignment.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
38
Use this information to answer the following questions.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.Assume that the road leading from factory F1 to retail outlet R1 is currently closed due to construction.How will this affect the shipping cost? Use Excel to formulate and solve this problem.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:

Refer to the information above.Assume that the road leading from factory F1 to retail outlet R1 is currently closed due to construction.How will this affect the shipping cost? Use Excel to formulate and solve this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
39
Consider the following data that illustrates demand,production costs,and expected capacity for a given product.
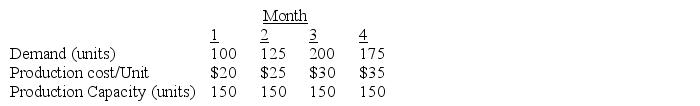
Inventory carrying costs are estimated at $4 per unit per month.The firm wants to produce at least 50 units per month to uniformly utilize its existing resources.Assume that beginning inventory is zero.Use Excel to formulate and solve this problem to determine how many units of the product should be produced monthly to meet the expected demand at minimal cost.
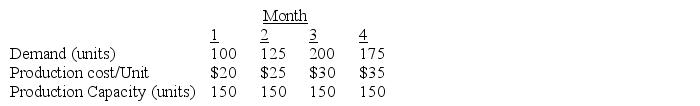
Inventory carrying costs are estimated at $4 per unit per month.The firm wants to produce at least 50 units per month to uniformly utilize its existing resources.Assume that beginning inventory is zero.Use Excel to formulate and solve this problem to determine how many units of the product should be produced monthly to meet the expected demand at minimal cost.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
40
Use this information to answer the following questions.
A beer distributor wants to prepare an aggregate plan for the next 6 weeks.Demand can be met using regular time production,overtime production,or a combination of both as illustrated below:

Refer to the table above.Assume that beginning inventory is zero.Use Excel to formulate and solve this multiperiod production problem to minimize total costs.
A beer distributor wants to prepare an aggregate plan for the next 6 weeks.Demand can be met using regular time production,overtime production,or a combination of both as illustrated below:

Refer to the table above.Assume that beginning inventory is zero.Use Excel to formulate and solve this multiperiod production problem to minimize total costs.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
41
Speedy Lube has 4 bays in its shop and 3 cars waiting for an oil change.The estimated time (in minutes)to change the oil and filter for each car in each bay is given as follows:

Which car should be assigned to which bay if Speedy Lube wants to minimize its total service time? Use Excel to formulate and solve this problem.

Which car should be assigned to which bay if Speedy Lube wants to minimize its total service time? Use Excel to formulate and solve this problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
42
A factory operates 7 days a week.Due to labor union regulations,employees are allowed to work a maximum of 5 consecutive days.The minimum number of employees that are needed on a given day is provided as follows:

Use Excel to formulate and solve this labor planning problem to determine the minimum number of employees needed each day.

Use Excel to formulate and solve this labor planning problem to determine the minimum number of employees needed each day.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
43
A real estate developer is planning to build an office complex.Currently,there are three office sizes under consideration: small,medium,and large.Small offices can be rented for $600 per month,medium offices can be rented for $750 per month,and large offices can be rented for $1000 per month.Each small office requires 600 square feet,each medium office requires 800 square feet,and each large office requires 1000 square feet.The current plot of land available to the developer is 100,000 square feet.The developer wants to ensure that the office complex has at least 3 units of each office size.Use Excel to formulate and solve this problem to maximize total revenue.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
44
A manufacturer of 19" LCD monitors encounters the following quarterly production cost,demand,and production capacity for its monitors:
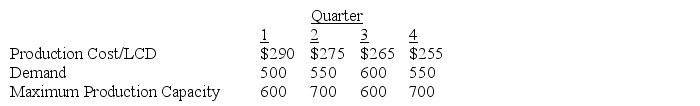
To maintain a stable workforce,the manufacturer wants to produce at least 500 units each quarter.To meet unexpected fluctuation in demand,the company wants to hold at least 100 monitors in stock each quarter.The cost of carrying a monitor in stock is $5 each quarter.Assume that beginning inventory is zero.Use Excel to formulate and solve this problem to determine to minimize production and inventory costs.
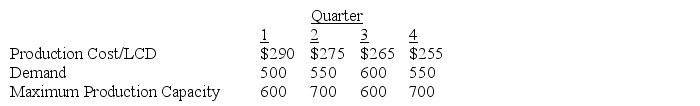
To maintain a stable workforce,the manufacturer wants to produce at least 500 units each quarter.To meet unexpected fluctuation in demand,the company wants to hold at least 100 monitors in stock each quarter.The cost of carrying a monitor in stock is $5 each quarter.Assume that beginning inventory is zero.Use Excel to formulate and solve this problem to determine to minimize production and inventory costs.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
45
A company is considering various advertising media to promote its new toy.Pertinent information regarding potential customers reached and costs per advertisement is given below:
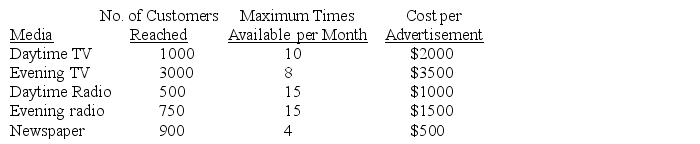
Currently,the company has a monthly advertising budget of $150,000.The marketing department has imposed the following restrictions:
•No more than $20,000 may be spent on radio advertising each month.
•At least 5 TV ads must be used each month.
Use Excel to formulate and solve this problem to maximize monthly audience exposure.

Currently,the company has a monthly advertising budget of $150,000.The marketing department has imposed the following restrictions:
•No more than $20,000 may be spent on radio advertising each month.
•At least 5 TV ads must be used each month.
Use Excel to formulate and solve this problem to maximize monthly audience exposure.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
46
A company manufactures two types of lawn mowers: riding mowers and push mowers.The company has the option of manufacturing the mowers in-house or outsourcing the entire operation.In-house manufacturing requires the following four operations: production,assembly,electrical wiring,and final inspection.The following table summarizes the weekly hours of processing time available and the processing time required by each operation.

The company has a weekly demand of 5 riding mowers and 3 push mowers.The company makes its riding mowers in-house for $500 each and its push mower for $200 each.Alternatively,it can outsource its riding and push mowers for $550 and $225 each,respectively.Use Excel to formulate and solve this "make" or "buy" problem.

The company has a weekly demand of 5 riding mowers and 3 push mowers.The company makes its riding mowers in-house for $500 each and its push mower for $200 each.Alternatively,it can outsource its riding and push mowers for $550 and $225 each,respectively.Use Excel to formulate and solve this "make" or "buy" problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
47
Three types of fertilizer are manufactured by a company-Regular,Supergro,and Jungle Feeder.Regular should have at least 10 percent nitrogen and 16 percent phosphorous.Supergro should have at least 12 percent nitrogen and 20 percent phosphorous,and Jungle Feeder should have at least 15 percent nitrogen and 18 percent phosphorous.These are made by using two components-A and B.Component A costs $0.30 per pound and is 14 percent nitrogen and 18 percent phosphorous.Component B costs $0.50 per pound and is 20 percent nitrogen and 24 percent phosphorous.The demand for Regular is projected to be 1000 pounds,while each of the others has a demand of 2000 pounds.Formulate and solve the appropriate linear program to determine how many pounds of Components A and B to include in each type of fertilizer,respectively.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
48
In a small suburban town,firefighters work 8-hour shifts.Assume there are six shifts each day that are divided into six 4-hour periods.The minimum number of firefighters needed on each shift is illustrated below.

Firefighters must report to work at the beginning of the above time periods and must work eight consecutive hours.Use Excel to formulate and solve this labor planning problem to determine the minimum number of firefighters needed on each shift.

Firefighters must report to work at the beginning of the above time periods and must work eight consecutive hours.Use Excel to formulate and solve this labor planning problem to determine the minimum number of firefighters needed on each shift.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
49
A furniture manufacturer produces three products,desks,tables,and chairs.These products can be produced during either the morning shift or the evening shift.The morning shift has a labor cost of $20 per hour with a maximum availability of 20,000 hours.The evening shift has a labor cost of $25 per hour and is limited to 15,000 hours.The labor,lumber,and demand requirements are given as follows:

Assume that there are 20,000 pounds of lumber and 20,000 pounds of nails available for both shifts.
Use Excel to formulate and solve this problem to minimize total labor cost.

Assume that there are 20,000 pounds of lumber and 20,000 pounds of nails available for both shifts.
Use Excel to formulate and solve this problem to minimize total labor cost.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck








