Deck 7: Feedback

Question 1

An amplifier with an open-loop gain of $1000 \mathrm{~V} / \mathrm{V}$ is connected in a feedback loop with the result that the closed-loop gain obtained is $10 \mathrm{~V} / \mathrm{V}$ .
(a) Find the value of the amount of feedback, the loop gain, and the feedback factor.
(b) If the open-loop gain varies by $\pm 10 \%$ , what is the corresponding variation of the closedloop gain?
(c) If the open-loop amplifier has 3-dB frequencies $f_{L}=1 \mathrm{kHz}$ and $f_{H}=100 \mathrm{kHz}$ , and the gain rolls off at the low and high frequency ends with a slope of $20 \mathrm{~dB} / \mathrm{decade}$ , find the $3-\mathrm{dB}$ frequencies of the closed-loop gain and sketch the Bode magnitude plot of both the open-loop and closed-loop gains (on the same axes).

Answer 1

$$A=1000 \mathrm{~V} / \mathrm{V}, \quad A_{f}=10 \mathrm{~V} / \mathrm{V}$$
(a)
$$\begin{aligned}A_{f} & =\frac{A}{1+A \beta} \\10 & =\frac{1000}{1+A \beta}\end{aligned}$$
Thus,
Amount of feedback $\equiv 1+A \beta=100$
$$\text { Loop gain } \equiv A \beta=99$$
Feedback factor $\equiv \beta=\frac{99}{1000}=0.099 \mathrm{~V} / \mathrm{V}$
(b)
$$\begin{aligned}\frac{\Delta A_{f}}{A_{f}} & =\frac{\triangle A / A}{1+A \beta} \\& =\frac{ \pm 10 \%}{100}= \pm 0.1 \%\end{aligned}$$
(c)
$$\begin{aligned}f_{L} & =1 \mathrm{kHz}, \quad f_{H}=100 \mathrm{kHz} \\f_{L f} & =\frac{f_{L}}{1+A \beta}=\frac{1000}{100}=10 \mathrm{~Hz} \\f_{H f} & =(1+A \beta) f_{H}=100 \times 100=10 \mathrm{MHz}\end{aligned}$$


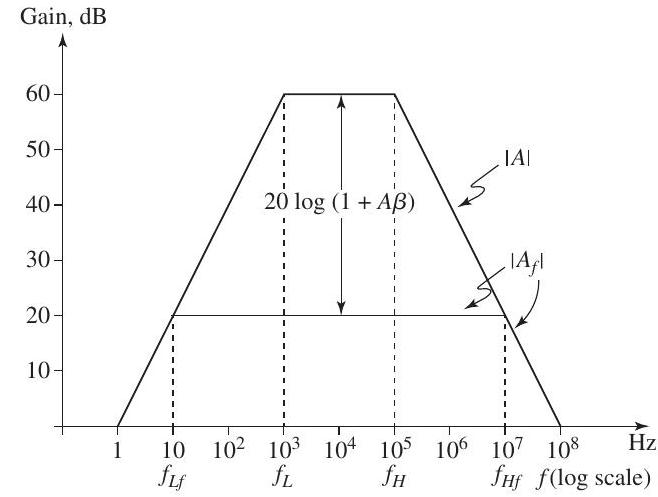
Figure 11.1.1
Sketches of the Bode plots for $|A|$ and $\left|A_{f}\right|$ are shown in Fig. 11.1.1.

Question 2

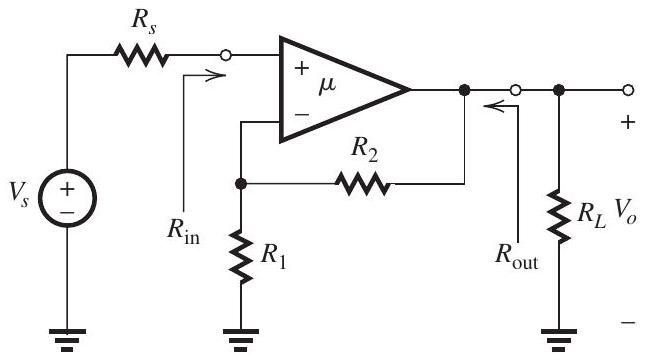
Figure 11.2.1
The series-shunt feedback amplifier shown in Fig. 11.2.1 utilizes a differential amplifier with a gain $\mu=10^{3}$ , input resistance $R_{i d}=100 \mathrm{k} \Omega$ , and output resistance $r_{o}=1 \mathrm{k} \Omega$ . The feedback amplifier is fed with a signal source $V_{S}$ having a source resistance $R_{S}=10 \mathrm{k} \Omega$ , and a load resistance $R_{L}=$ $1 \mathrm{k} \Omega$ is connected to the output terminal.
(a) If it is required to obtain a closed-loop gain $A_{f} \equiv V_{o} / V_{S}$ that is ideally $10 \mathrm{~V} / \mathrm{V}$ , what is the required feedback factor $\beta$ ? If $R_{1}=1 \mathrm{k} \Omega$ , what value must $R_{2}$ have?
(b) Give the complete $A$ circuit and use it to determine $A, R_{i}$ , and $R_{o}$ .
(c) Find the actual value of $A_{f}$ realized.
(d) Find the input resistance $R_{\text {in }}$ of the feedback amplifier.
(e) Find the output resistance $R_{\text {out }}$ of the feedback amplifier.
(f) If, due to temperature variation, the gain $\mu$ changes by $10 \%$ , what percentage change do you expect $A_{f}$ to have?
(g) If the high-frequency response of the amplifier $\mu$ is characterized by a drop of $20 \mathrm{~dB} /$ decade with a 3-dB frequency of $10 \mathrm{kHz}$ , what do you expect the 3-dB frequency of the gain $A_{f}$ to be? At what frequency will the magnitude of $A_{f}$ become unity?

Answer 2

Figure 11.2.1
(a) For $A_{f}$ to be ideally $10 \mathrm{~V} / \mathrm{V}$ ,
$$\beta=\frac{1}{A_{f}}=0.1 \mathrm{~V} / \mathrm{V}$$


Figure 11.2.2
From the feedback network shown in Fig. 11.2.2,
$$\begin{aligned}\beta & =\frac{R_{1}}{R_{1}+R_{2}} \\0.1 & =\frac{1}{1+R_{2}} \\\Rightarrow R_{2} & =9 \mathrm{k} \Omega\end{aligned}$$
(b) The $A$ circuit is shown in Fig. 11.2.3 (refer to Figure below).
Figure 11.2.3
$$\begin{aligned}A & =\frac{V_{o}}{V_{i}}=\frac{V_{1}}{V_{i}} \frac{V_{o}}{V_{1}} \\& =\frac{R_{i d}}{R_{S}+R_{i d}+\left(R_{1} \| R_{2}\right)} \mu \frac{R_{L} \|\left(R_{1}+R_{2}\right)}{\left[R_{L} \|\left(R_{1}+R_{2}\right)\right]+r_{o}} \\& =\frac{100}{10+100+(1 \| 9)} \times 10^{3} \times \frac{1 \|(1+9)}{[1 \|(1+9)]+1} \\& =429.4 \mathrm{~V} / \mathrm{V} \\R_{i} & =R_{S}+R_{i d}+\left(R_{1} \| R_{2}\right) \\& =10+100+(1 \| 9) \\& =110.9 \mathrm{k} \Omega \\R_{O} & =R_{L}\left\|\left(R_{1}+R_{2}\right)\right\| r_{o} \\& =1\|(1+9)\| 1 \\& =476.2 \Omega\end{aligned}$$
(c)
$$\begin{aligned}A_{f} & =\frac{A}{1+A \beta} \\& =\frac{429.4}{1+429.4 \times 0.1} \\& =9.77 \mathrm{~V} / \mathrm{V}\end{aligned}$$
(d)
$$\begin{aligned}R_{i f} & =(1+A \beta) R_{i} \\& =(1+429.4 \times 0.1) \times 110.9 \\& =4.873 \mathrm{M} \Omega \\R_{\text {in }} & =R_{i f}-R_{S}=4873-10 \\& =4.863 \mathrm{M} \Omega\end{aligned}$$
(e)
$$\begin{aligned}R_{o f} & =\frac{R_{o}}{1+A \beta} \\& =\frac{476.2}{43.94}=10.84 \Omega\end{aligned}$$
Since
$$\begin{aligned}\frac{1}{R_{\text {of }}} & =\frac{1}{R_{L}}+\frac{1}{R_{\mathrm{out}}} \\\Rightarrow R_{\mathrm{out}} & =10.96 \Omega\end{aligned}$$
(f)
$$\begin{aligned}\frac{\triangle \mu}{\mu} & =10 \% \\\Rightarrow \frac{\triangle A}{A} & =10 \% \\\Rightarrow \frac{\triangle A_{f}}{A_{f}} & =\frac{\triangle A / A}{1+A \beta} \\& =\frac{10}{43.94}=0.23 \%\end{aligned}$$
(g)
$$\begin{aligned}f_{H f} & =(1+A \beta) f_{H} \\& =43.94 \times 10 \\& =439.4 \mathrm{kHz}\end{aligned}$$
$\left|A_{f}\right|$ reaches unity at
$$\begin{aligned}f_{t} & =\left|A_{f}\right| \times f_{H f}=9.77 \times 439.4 \\& =4.29 \mathrm{MHz}\end{aligned}$$

Question 3

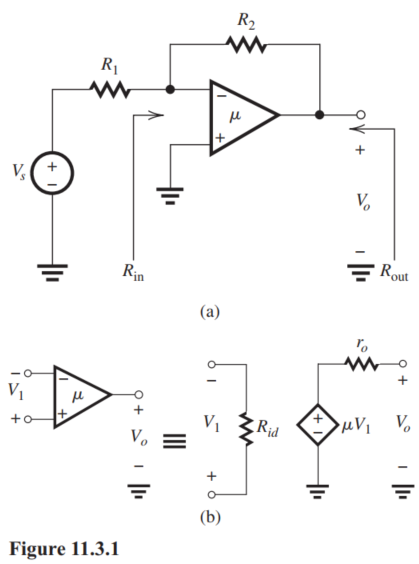
The feedback amplifier shown in Fig. 11.3.1(a) employs the shunt-shunt feedback topology. To see this more clearly and to apply the feedback analysis method, convert the signal source $V_{S}$ together with the resistance $R_{1}$ to its Norton's equivalent circuit composed of current source $I_{S}=$ $V_{S} / R_{1}$ together with a parallel resistance equal to $R_{1}$ . The amplifier $\mu$ has the equivalent circuit shown in Fig. 11.3.1(b). We wish to investigate the case for which $\mu=10^{3} \mathrm{~V} / \mathrm{V}, R_{i d}=1 \mathrm{M} \Omega$ , $r_{o}=100 \Omega, R_{1}=1 \mathrm{k} \Omega$ , and $R_{2}=100 \mathrm{k} \Omega$ .
(a) Find the $A$ circuit and derive expressions for $A \equiv V_{o} / I_{S}, R_{i}$ , and $R_{o}$ . Evaluate these expressions to determine $A, R_{i}$ , and $R_{o}$ .
(b) Find the $\beta$ circuit and derive an expression for $\beta$ . Find the value of $\beta$ .
(c) Find an expression for $A \beta$ and its value.
(d) Find the value of the amount of feedback.
(e) Find the closed-loop gain and hence $V_{o} / V_{S}$ .
(f) Find the value of $R_{\text {in }}$ .
(g) Find the value of $R_{\text {out }}$ .
(h) If $\mu$ changes by $-10 \%$ , what is the resulting change in $V_{o} / V_{S}$ ?

Answer 3

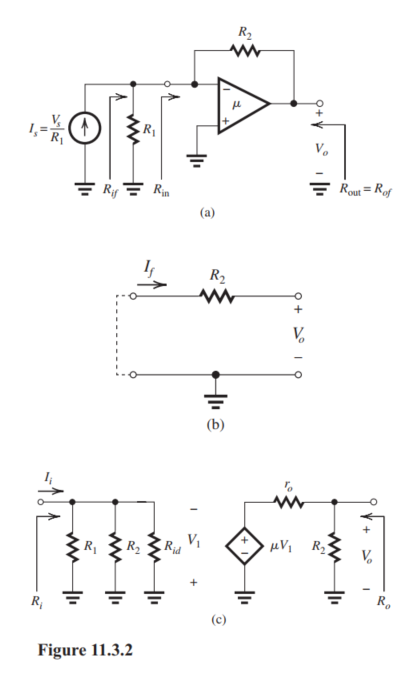
(a) Figure 11.3.2(a) shows the shunt-shunt feedback amplifier (transresistance amplifier) with $V_{S}$ and $R_{1}$ converted to the Norton form. The $\beta$ circuit is shown in Fig. 11.3.2(b) and the $A$ circuit is shown in Fig. 11.3.2(c). From the latter,
$$\begin{aligned}R_{i} & =R_{1}\left\|R_{2}\right\| R_{i d} \\& =1\|100\| 1000=989.1 \Omega \\V_{1} & =-I_{i} R_{i} \\V_{o} & =\mu V_{1} \frac{R_{2}}{R_{2}+r_{o}}\end{aligned}$$
Thus,
$$\begin{aligned}A & \equiv \frac{V_{o}}{I_{i}}=-\mu R_{i} \frac{R_{2}}{R_{2}+r_{o}} \\A & =-\mu\left(R_{1}\left\|R_{2}\right\| R_{i d}\right) \frac{R_{2}}{R_{2}+r_{o}} \\A & =-10^{3} \times 0.9891 \times \frac{100}{100+0.1} \\& =-988.1 \mathrm{k} \Omega \\R_{O} & =R_{2} \| r_{o} \\R_{O} & =100 \mathrm{k} \Omega \| 100 \Omega=99.9 \Omega\end{aligned}$$
(b) The $\beta$ circuit is shown in Fig. 11.3.2(b).
$$\begin{aligned}& \beta \equiv \frac{I_{f}}{V_{o}}=-\frac{1}{R_{2}} \\& \beta=-\frac{1}{100}=-0.01 \mathrm{~mA} / \mathrm{V}\end{aligned}$$
(c)
$$\begin{aligned}A \beta & =-\mu\left(R_{1}\left\|R_{2}\right\| R_{i d}\right) \frac{R_{2}}{R_{2}+r_{o}} \times \frac{-1}{R_{2}} \\A \beta & =\mu \frac{R_{1}\left\|R_{2}\right\| R_{i d}}{R_{2}+r_{o}} \\& =10^{3} \times \frac{989.1 \Omega}{100.1 \mathrm{k} \Omega} \\& =9.88\end{aligned}$$
(d)
$$1+A \beta=10.88$$
(e)
$$\begin{gathered}A_{f} \equiv \frac{V_{o}}{I_{S}}=\frac{A}{1+A \beta}=-\frac{988.1 \mathrm{k} \Omega}{10.88}=-90.8 \mathrm{k} \Omega \\\frac{V_{o}}{V_{S}}=\frac{V_{o}}{I_{S} R_{1}}=-\frac{90.8 \mathrm{k} \Omega}{1 \mathrm{k} \Omega}=-90.8 \mathrm{~V} / \mathrm{V}\end{gathered}$$
(f)
$$R_{i f}=\frac{R_{i}}{1+A \beta}=\frac{989.1}{10.88}=90.9 \Omega$$
But,
$$\begin{aligned}\frac{1}{R_{\text {if }}} & =\frac{1}{R_{\text {in }}}+\frac{1}{R_{1}} \\\Rightarrow R_{\text {in }} & =1 /\left(\frac{1}{90.9}-\frac{1}{1000}\right)=100 \Omega\end{aligned}$$
(g)
$$R_{\mathrm{out}}=R_{o f}=\frac{R_{o}}{1+A \beta}=\frac{99.9}{10.88}=9.2 \Omega$$
(h)
$$\begin{aligned}& \frac{\triangle \mu}{\mu}=-10 \% \\& \Rightarrow \frac{\triangle A}{A}=-10 \% \\& \Rightarrow \frac{\triangle A_{f}}{A_{f}}=\frac{\triangle A / A}{1+A \beta}=-\frac{10}{10.88}=-0.92 \% \\& \Rightarrow \text { Change in } \frac{V_{o}}{V_{S}} \text { is }-0.92 \%\end{aligned}$$


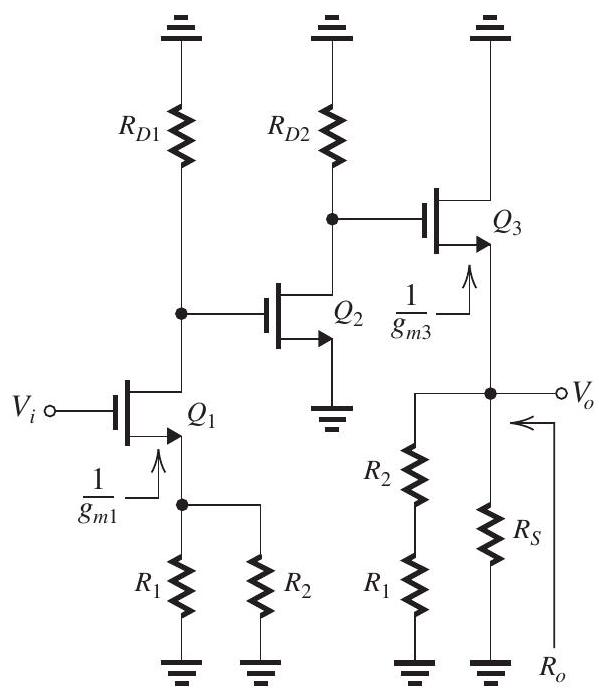
Figure 11.4.3

Question 4

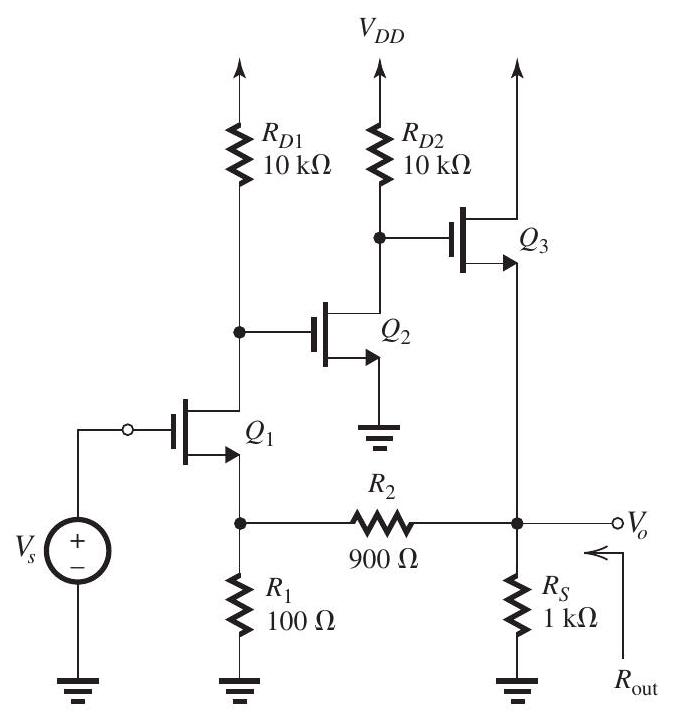
Figure 11.4.1
The series-shunt feedback amplifier shown in Fig. 11.4.1 uses a feedback network $\left(R_{1}, R_{2}\right)$ to sample the output voltage $V_{o}$ . Though the bias details are not shown, it is known that each of $Q_{1}$ , $Q_{2}$ , and $Q_{3}$ is operating at a $g_{m}$ of $2 \mathrm{~mA} / \mathrm{V}$ and that their $r_{o}$ 's are very large.
(a) Give the $\beta$ circuit and find the value of $\beta$ .
(b) What do you estimate the approximate value of the closed-loop gain $A_{f}=V_{o} / V_{S}$ to be?
(c) Give the $A$ circuit and calculate the value of $A$ .
(d) Use the results of (a) and (c) to determine $A_{f}$ and compare the result to the value obtained in (b).
(e) Find the output resistance $R_{O}$ of the $A$ circuit.
(f) Find the output resistance $R_{\text {out }}$ of the closedloop amplifier.
(g) If the open-loop gain $A$ is found to have a dominant high-frequency pole at $1 \mathrm{MHz}$ , what do you expect the upper 3-dB frequency of the closed-loop gain $A_{f}$ to be?
(h) If for some reason $g_{m}$ of $Q_{2}$ decreases by $20 \%$ , what is the corresponding percentage decrease in $A_{f}$ ?

Question 5

The feedback voltage amplifier in Fig. 11.5.1

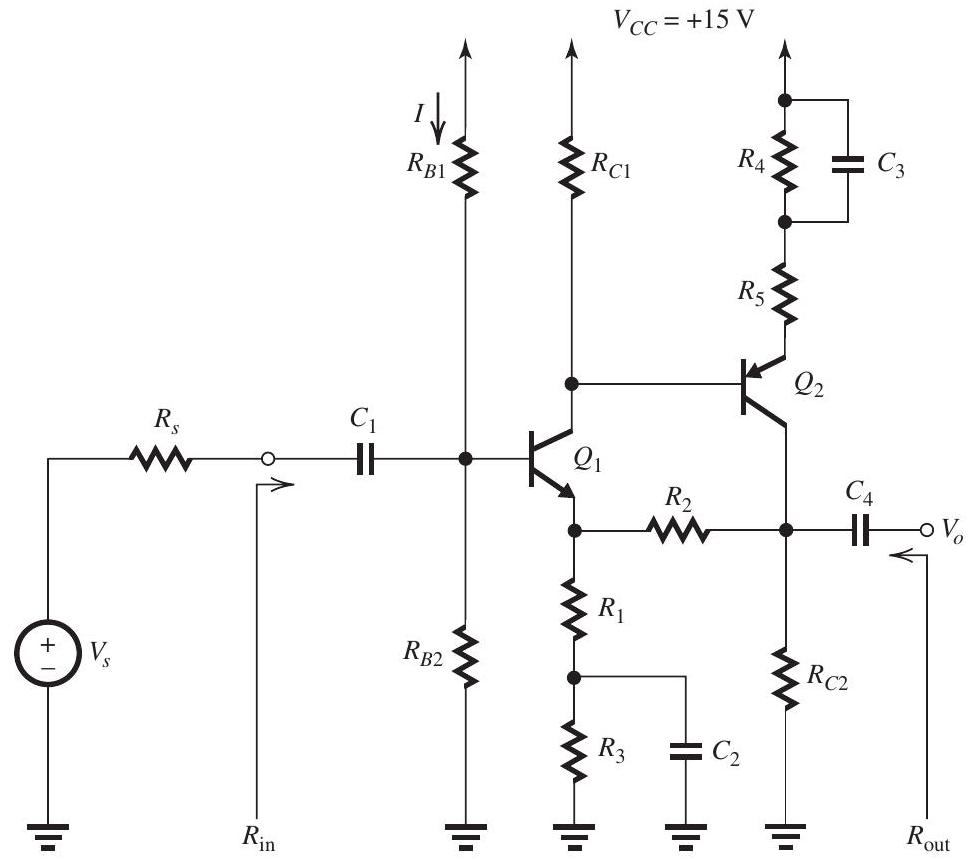
Figure 11.5.1
utilizes the series-shunt feedback topology with the feedback network composed of $R_{1}$ and $R_{2}$ . The following component values are given: $R_{S}=5 \mathrm{k} \Omega, R_{1}=1 \mathrm{k} \Omega, R_{2}=$ $11 \mathrm{k} \Omega$ , and $R_{5}=300 \Omega$ . The BJTs have $\beta=100$ , $\left|V_{B E}\right|=0.7 \mathrm{~V}$ , and $r_{o}=\infty$ . The capacitors $C_{1}, C_{2}$ , $C_{3}$ , and $C_{4}$ are very large.
(a) Find values for $R_{B 1}, R_{B 2}, R_{3}, R_{C 1}, R_{4}$ , and $R_{C 2}$ so as to establish the following de conditions: $V_{B 1}=+4 \mathrm{~V}, V_{C 1}=+6 \mathrm{~V}, V_{C 2}=+4 \mathrm{~V}, I_{E 1}=$ $I_{E 2}=1 \mathrm{~mA}$ , and $I=0.1 \mathrm{~mA}$ . Hint: Do as many of your calculations as possible on Fig. 11.5.1 on the exam paper.
(b) Supply the $A$ circuit and find the values of $A$ , $R_{i}$ , and $R_{O}$ .
(c) Supply the $\beta$ circuit and find the value of $\beta$ .
(d) Find the closed-loop gain $A_{f} \equiv V_{o} / V_{s}$ , the input resistance $R_{\mathrm{in}}$ , and the output resistance $R_{\text {out. }}$

Question 6

Figure 11.6.1 (refer to Figure below)


Figure 11.6.1
shows a feedback voltage amplifier in which the basic amplifier is composed of three cascaded stages having the following characteristics:
$A_{1}$ has a differential input resistance of $82 \mathrm{k} \Omega$ , an open-circuit differential voltage gain of $20 \mathrm{~V} / \mathrm{V}$ , and an output resistance of $3.2 \mathrm{k} \Omega$ .
$A_{2}$ has an input resistance of $5 \mathrm{k} \Omega$ , a shortcircuit tranconductance of $20 \mathrm{~mA} / \mathrm{V}$ , and an output resistance of $20 \mathrm{k} \Omega$ . $A_{3}$ has an input resistance of $20 \mathrm{k} \Omega$ , an opencircuit voltage gain of unity, and an output resistance of $1 \mathrm{k} \Omega$ .
The feedback amplifier is fed with a signal source having $R_{S}=9 \mathrm{k} \Omega$ and is connected to a load $R_{L}=1 \mathrm{k} \Omega$ . The feedback network has $R_{1}=10 \mathrm{k} \Omega$ and $R_{2}=90 \mathrm{k} \Omega$ .
(a) Give the $A$ circuit and find the value of $A$ .
(b) Find $\beta$ and the amount of feedback.
(c) Find the closed-loop gain $A_{f} \equiv V_{o} / V_{s}$ .
(d) Find the input resistance $R_{\text {in }}$ .
(e) Find the output resistance $R_{\text {out }}$ .
(f) If the high-frequency response of the openloop gain $A$ is dominated by a pole at $1 \mathrm{kHz}$ , what is the upper 3-dB frequency of the closed-loop gain?
(g) If for some reason the gain of $A_{1}$ drops to half its nominal value, what is the percentage change in $A_{f}$ ?

Question 7

In the circuit of Fig. 11.7.1 (refer to Figure below), assume that coupling capacitors $C_{C 1}$ and $C_{C 2}$ are very large and thus act as perfect short circuits at


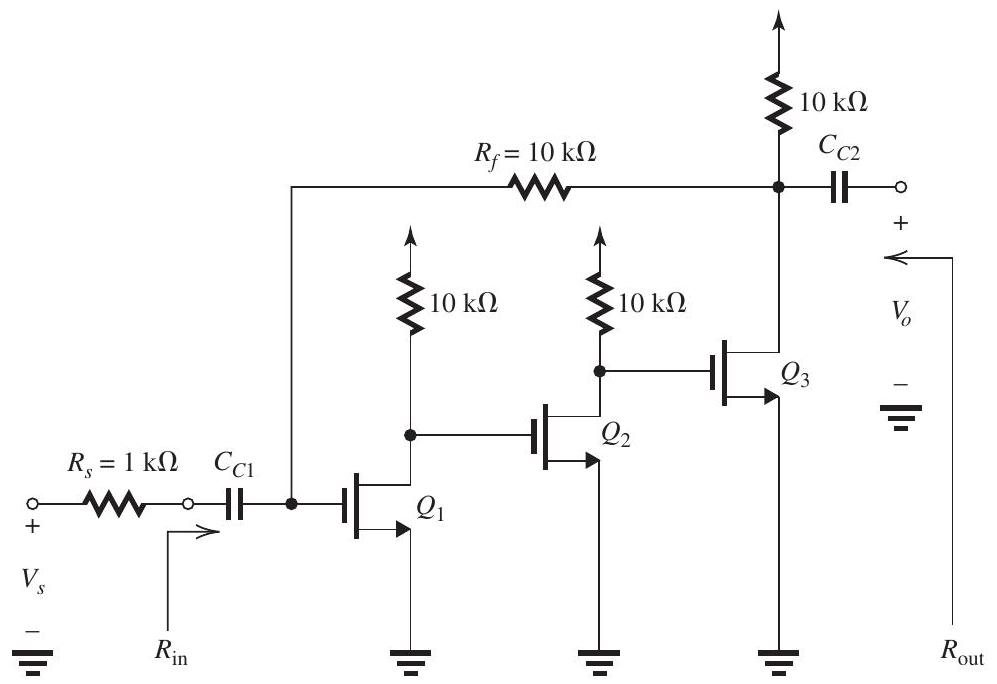
Figure 11.7.1
the frequencies of interest. Transistors $Q_{1}, Q_{2}$ , and $Q_{3}$ are identical and are operating at identical dc bias conditions so that each has $g_{m}=5 \mathrm{~mA} / \mathrm{V}$ and $r_{o}=10 \mathrm{k} \Omega$ .
(a) Replacing the signal source $V_{S}$ and $R_{S}$ with its Norton's equivalent circuit, show that this feedback amplifier utilizes the shunt-shunt feedback topology.
(b) Give the $\beta$ circuit and determine the value of $\beta$ .
(c) Give the ideal value of the closed-loop gain and hence of the voltage gain $V_{o} / V_{S}$ .
(d) Provide the $A$ circuit and determine the values of $A, R_{i}$ , and $R_{o}$ .
(e) Find the values of $A_{f}, R_{i f}$ , and $R_{o f}$ .
(f) Find the actual value of voltage gain $V_{o} / V_{S}$ realized and compare to the approximate value found in (c).
(g) Find the value of $R_{\text {in }}$ ,
(h) Find the value of $R_{\text {out }}$ .
(i) If $V_{s}$ is $100 \mathrm{mV}$ , find the magnitudes of the signals at the gates of $Q_{1}, Q_{2}$ , and $Q_{3}$ and at the output (i.e., $V_{o}$ ).

Question 8

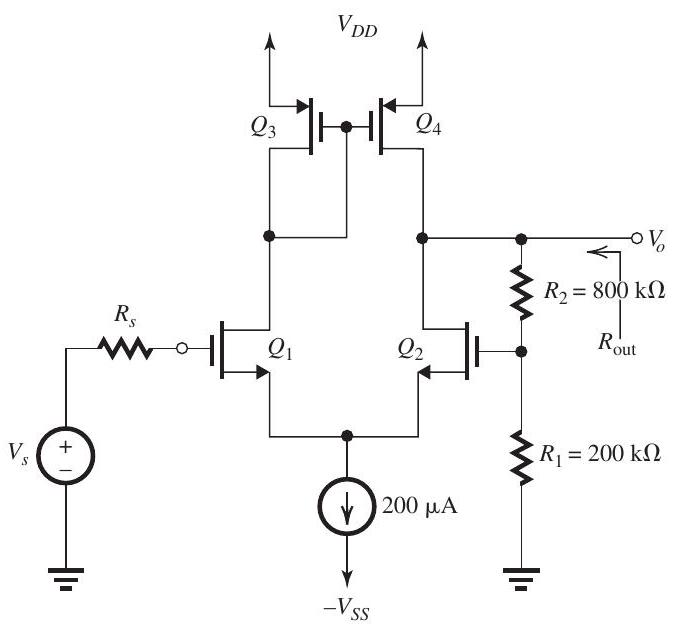
Figure 11.8.1
Figure 11.8.1 shows a MOS current-mirrorloaded differential amplifier with negative feedback applied through a voltage divider $\left(R_{1}, R_{2}\right)$ . Each of the four MOS transistors is operating at an overdrive voltage $\left|V_{O V}\right|=0.2 \mathrm{~V}$ and has an Early voltage $\left|V_{A}\right|=20 \mathrm{~V}$ .
(a) Find expressions for $\beta$ and for the ideal value of the closed-loop gain $V_{o} / V_{s}$ . Hence, find the value of $\beta$ and the ideal value of $V_{o} / V_{S}$ .
(b) Give the $A$ circuit and expressions for $A$ and $R_{O}$ . Hence, find the values of the open-loop gain $A$ and the open-loop output resistances $R_{O}$ .
(c) Find the value of the closed-loop gain $A_{f} \equiv$ $V_{o} / V_{S}$ . Compare to the ideal value found in (a).
(d) Find the value of the output resistance $R_{\text {out }}$ .

Question 9

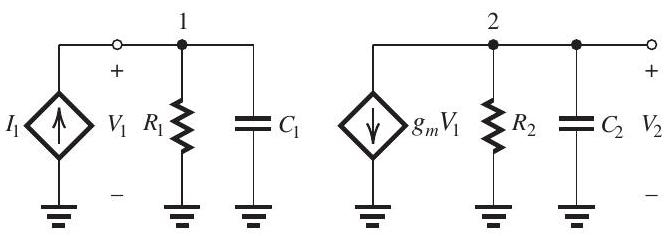
Figure 11.9.1
An op amp has a dc gain of $100 \mathrm{~dB}$ and three real-axis poles with frequencies $f_{P 1}=10^{4} \mathrm{~Hz}$ , $f_{P 2}=10^{5} \mathrm{~Hz}$ , and $f_{P 3}=10^{6} \mathrm{~Hz}$ . The op-amp internal circuit includes an amplifier stage having the equivalent circuit shown in Fig. 11.9.1, where $C_{1}=100 \mathrm{pF}, g_{m}=20 \mathrm{~mA} / \mathrm{V}$ , and $C_{2}=10 \mathrm{pF}$ . Furthermore, it is found that the input circuit of this stage is responsible for the pole at $f_{P 1}$ and that the output circuit is responsible for the pole at $f_{P 2}$ . It is required to frequency-compensate this op amp so that it becomes stable in closed-loop configurations with a closed-loop gain as low as unity.
(a) Sketch and clearly label a Bode plot for the op amp gain. Use a frequency axis that extends from $0.1 \mathrm{~Hz}$ to $10^{7} \mathrm{~Hz}$ .
(b) If the frequency compensation is achieved by connecting a capacitor $C_{C}$ in parallel with $C_{1}$ , find the required value of $C_{C}$ and sketch the modified gain response on your Bode plot.
(c) If the frequency compensation is achieved by placing a capacitor $C_{f}$ in the feedback path of the amplifier stage in Fig. 11.9.1 -that is, between nodes 1 and 2 (Miller compensation)-find the required value of $C_{f}$ . Also, find the new frequencies of the poles and sketch the modified gain on your Bode plot.