Deck 5: Differential and Multistage Amplifiers

Question 1

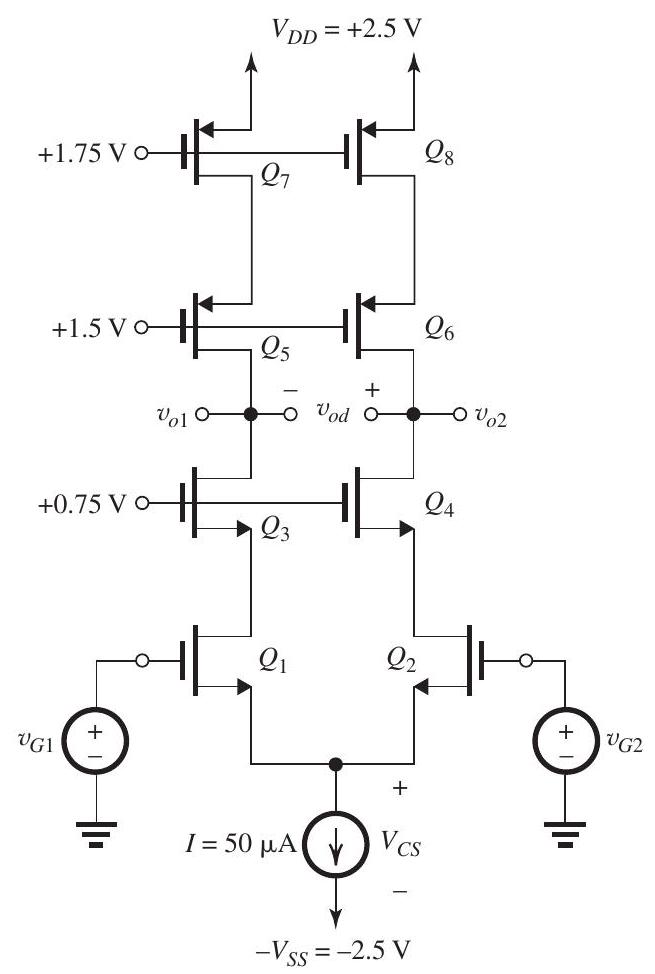
Figure 9.1.1
For the differential cascode amplifier in Fig. 9.1.1, all the transistors have the same threshold voltage $\left|V_{t}\right|=0.5 \mathrm{~V}$ and are operating at the same overdrive voltage. For the purpose of calculating dc quantities, neglect the Early effect. The current source $I$ requires a minimum dc voltage $V_{C S}=0.25 \mathrm{~V}$ for its proper operation.
(a) With $v_{G 1}=v_{G 2}=0 \mathrm{~V}$ , find:
i. The bias current in each of the eight transistors.
ii. $\left|V_{O V}\right|$ for each of the eight transistors. iii. $g_{m}$ for each transistor.
iv. $r_{O}$ and $A_{0}$ for each transistor assuming $\left|V_{A}\right|=$ $5 \mathrm{~V}$ .
v. The dc voltage at the drains of $Q_{1}$ and $Q_{2}$ .
(b) Find the input common-mode range.
(c) With $v_{G 1}=v_{i d} / 2$ and $v_{G 2}=-v_{i d} / 2$ , where $v_{i d} \ll 2 V_{O V}$ , give the differential half-circuit and use it to determine the differential gain $v_{o d} / v_{i d}$ .

Answer 1

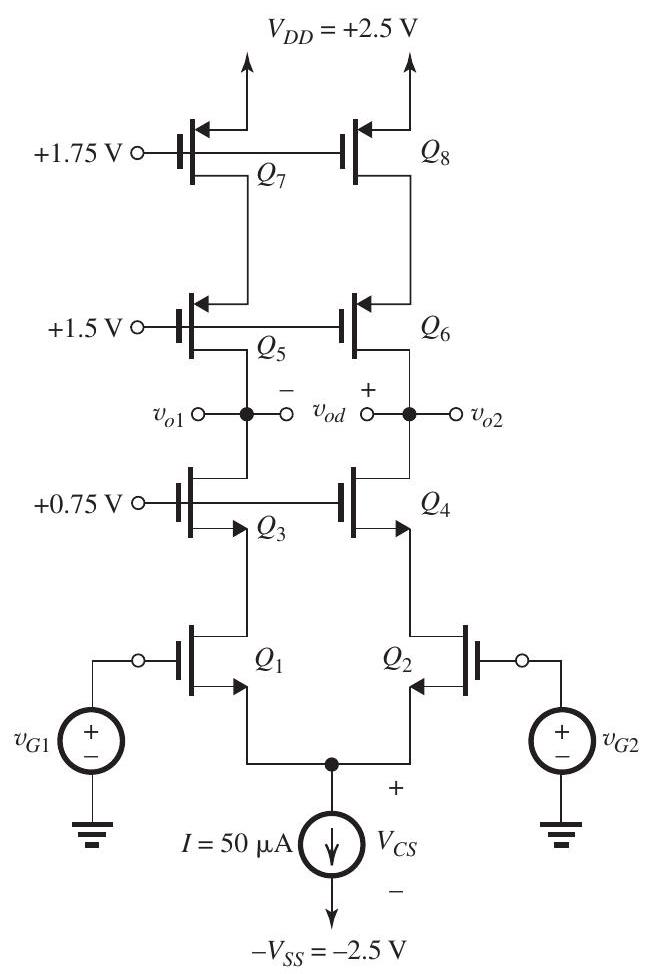
Figure 9.1.1
(a)
(i)
$$I_{D}=\frac{I}{2}=25 \mu \mathrm{A}$$
(ii) Since for $Q_{7}$ and $Q_{8}$ ,
$$V_{S G}=2.5-1.75=0.75 \mathrm{~V}$$
and since all transistors have the same $\left|V_{t}\right|$ and $\left|V_{O V}\right|$ , then
$$\left|V_{O V}\right|=0.75-0.5=0.25 \mathrm{~V}$$
(iii)
$$g_{m}=\frac{2 I_{D}}{\left|V_{O V}\right|}=\frac{2 \times 0.025}{0.25}=0.2 \mathrm{~mA} / \mathrm{V}$$
(iv)
$$\begin{aligned}r_{o} & =\frac{\left|V_{A}\right|}{I_{D}}=\frac{5}{0.025}=200 \mathrm{k} \Omega \\A_{0} & =g_{m} r_{o}=0.2 \times 200=40\end{aligned}$$
(v)
$$V_{D 1}=V_{D 2}=0.75-V_{G S 3,4}=0 \mathrm{~V}$$
(b)
$$\begin{aligned}v_{I C M \max } & =V_{D 1}+V_{t}=0+0.5=0.5 \mathrm{~V} \\v_{I C M \min } & =-V_{S S}+V_{C S}+V_{G S 1,2} \\& =-2.5+0.25+0.75=-1.5 \mathrm{~V}\end{aligned}$$
Thus,
(c)


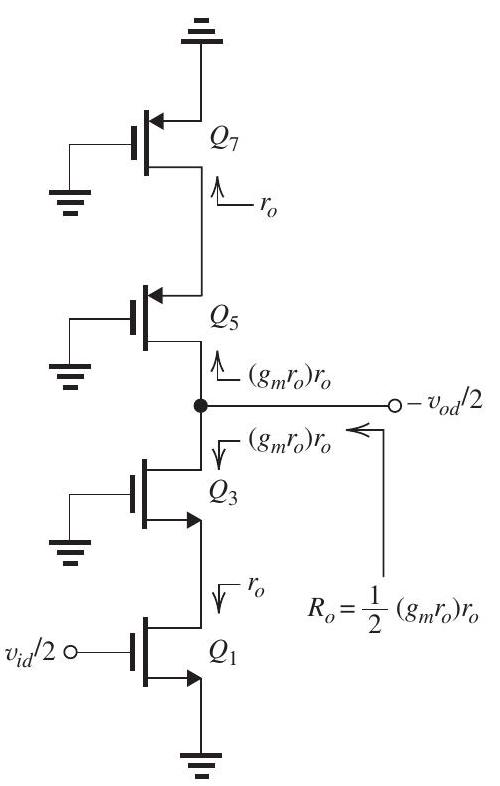
Figure 9.1.2
From the differential half-circuit in Fig. 9.1.2, we find
$$\begin{aligned}\frac{v_{o d}}{v_{i d}} & =g_{m 1} R_{O} \\& =g_{m} \times \frac{1}{2}\left(g_{m} r_{o}\right) r_{o} \\& =\frac{1}{2}\left(g_{m} r_{o}\right)^{2} \\& =\frac{1}{2} A_{0}^{2}=\frac{1}{2} \times 40^{2}=800 \mathrm{~V} / \mathrm{V}\end{aligned}$$

Question 2

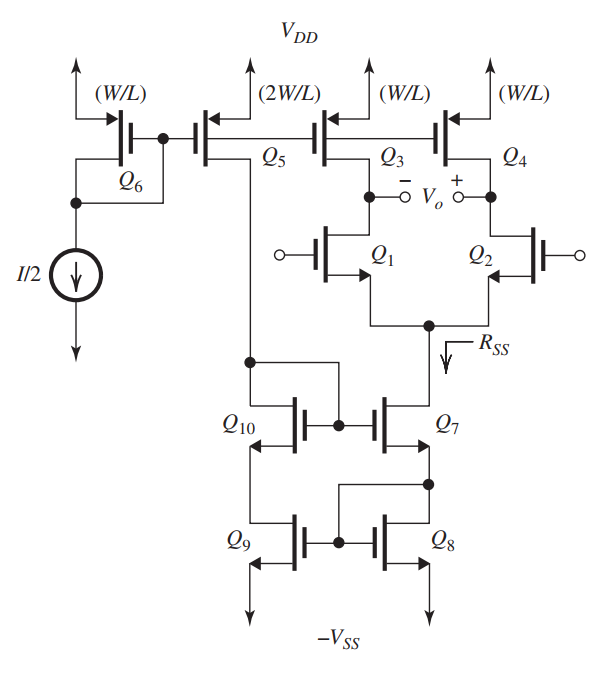
Figure 9.2.1
The differential amplifier in Fig. 9.2.1 utilizes current-source loads and is biased with a modified Wilson current mirror. All transistors are operated at the same overdrive voltage $\left|V_{O V}\right|=0.2 \mathrm{~V}$ and have equal Early voltage, $\left|V_{A}\right|=4 \mathrm{~V}$ .
(a) Find the differential gain.
(b) Find the CMRR (in $\mathrm{dB}$ ) assuming that the
only mismatch is that between $g_{m 1}$ and $g_{m 2}$ with $\triangle g_{m} / g_{m}=0.01$ .
(c) If the Wilson mirror is replaced with a simple current mirror, what does the CMRR become?

Answer 2

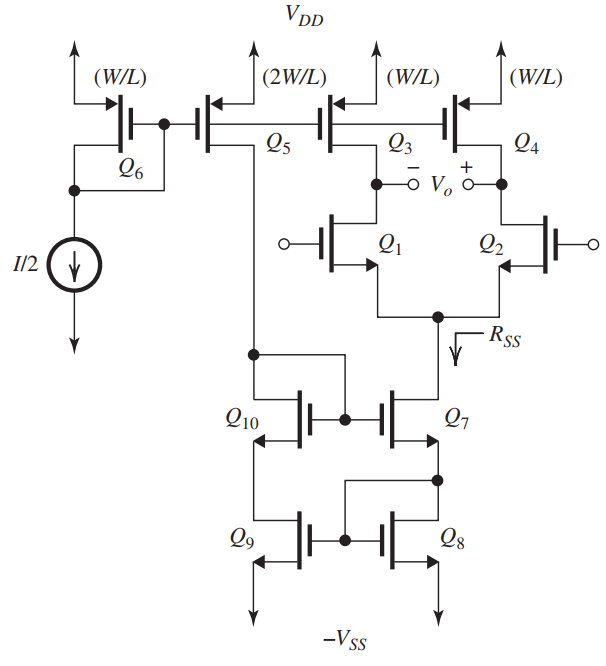
Figure 9.2.1 (a)
$$A_{d}=g_{m 1}\left(r_{o 1} \| r_{o 3}\right)$$
where
$$\begin{aligned}g_{m 1} & =\frac{2 I_{D}}{\left|V_{O V}\right|} \\r_{o 1} & =r_{o 3}=\frac{\left|V_{A}\right|}{I_{D}} \\A_{d} & =\frac{2 I_{D}}{\left|V_{O V}\right|} \times \frac{1}{2} \frac{\left|V_{A}\right|}{I_{D}} \\& =\frac{\left|V_{A}\right|}{\left|V_{O V}\right|}=\frac{4}{0.2}=20 \mathrm{~V} / \mathrm{V}\end{aligned}$$
(b)
$$\mathrm{CMRR}=\left(2 g_{m 1} R_{S S}\right) /\left(\frac{\triangle g_{m}}{g_{m}}\right)$$
where
$$\begin{aligned}R_{S S} & =\left(g_{m 7} r_{o 7}\right) r_{o 9} \\& =\frac{2 I_{D 7}}{\left|V_{O V}\right|} \times \frac{V_{A}}{I_{D 7}} \times \frac{V_{A}}{I_{D 9}} \\& =\frac{2 V_{A}}{\left|V_{O V}\right|} \frac{V_{A}}{I_{D 9}}\end{aligned}$$
But
$$I_{D 9}=2 \times \frac{I}{2}=I$$
and
$$g_{m 1}=\frac{2 I_{D 1}}{\left|V_{O V}\right|}=\frac{2 \times\left(\frac{I}{2}\right)}{\left|V_{O V}\right|}=\frac{I}{\left|V_{O V}\right|}$$
Thus,
$$\begin{aligned}\mathrm{CMRR} & =\frac{2 I}{\left|V_{O V}\right|} \times \frac{2\left|V_{A}\right|}{\left|V_{O V}\right|} \times \frac{\left|V_{A}\right|}{I} \times \frac{1}{0.01} \\& =400\left|\frac{V_{A}}{V_{O V}}\right|^{2}=400 \times\left(\frac{4}{0.2}\right)^{2} \\& =1.6 \times 10^{5}\end{aligned}$$
or
$$20 \log \left(1.6 \times 10^{5}\right)=104 \mathrm{~dB}$$
(c) If the Wilson mirror is replaced with a simple current mirror,
$$R_{S S}=r_{o}=\frac{\left|V_{A}\right|}{I}$$
Thus,
$$\begin{aligned}\mathrm{CMRR} & =\frac{2 I}{\left|V_{O V}\right|} \times \frac{\left|V_{A}\right|}{I} \times \frac{1}{0.01} \\& =200\left|\frac{V_{A}}{V_{O V}}\right|=200 \times\left(\frac{4}{0.2}\right) \\& =4000\end{aligned}$$
or $72 \mathrm{~dB}$

Question 3

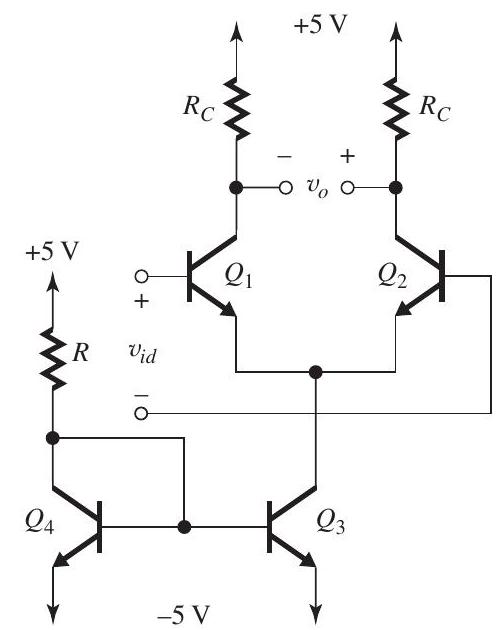
Figure 9.3.1
For the amplifier in Fig. 9.3.1:
(a) Assuming $Q_{3}$ and $Q_{4}$ have very high $\beta$ values, determine the value of $R$ that will provide a dc current of $0.25 \mathrm{~mA}$ for each of $Q_{1}$ and $Q_{2}$ . (b) Assuming $Q_{1}$ and $Q_{2}$ have very high $\beta$ values, determine the value of $R_{C}$ that results in a dc voltage of $+3 \mathrm{~V}$ at the collectors of $Q_{1}$ and $Q_{2}$ .
(c) What is the input common-mode range for this differential amplifier?
(d) Determine the value of the differential voltage gain $v_{O} / v_{i d}$ .
(e) Determine the value of the input differential resistance, $R_{i d}$ . Assume $\beta_{1}=\beta_{2}=100$ .
(f) If it is required to raise the value of $R_{i d}$ by factor of 5 by including a resistance $R_{E}$ in the emitter of each of $Q_{1}$ and $Q_{2}$ , what value of $R_{E}$ is required? What is the resulting value of the differential gain?
(g) If the transistors have an Early voltage $V_{A}=50 \mathrm{~V}$ , calculate the worst-case value of the common-mode gain resulting from the resistances $R_{C}$ having finite tolerances of $\pm 1 \%$ . Hence, find the value of the CMRR of the original amplifier (i.e., the one without the resistances $R_{E}$ included).
(h) With the two input terminals grounded, calculate the value of the worst-case differential dc voltage at the output resulting from the resistances $R_{C}$ having finite tolerances of $\pm 1 \%$ . Hence, find the input offset voltage of the original amplifier (i.e., the one without $R_{E}$ 's).

Answer 3

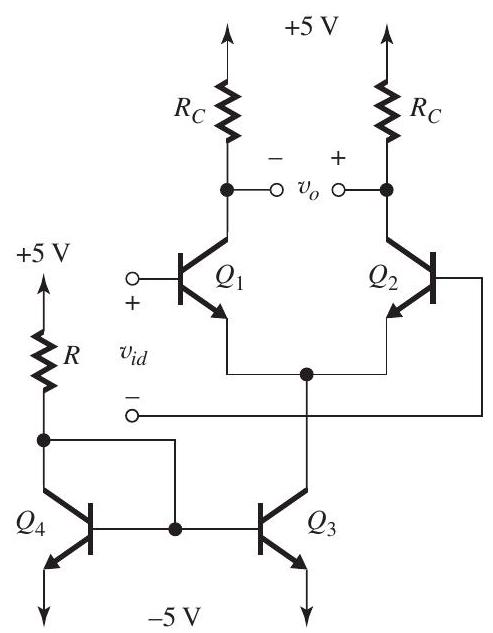
Figure 9.3.1
(a) To obtain a $0.25-\mathrm{mA}$ current in each of $Q_{1}$ and $Q_{2}$ , the current in $Q_{3}$ must be $0.5 \mathrm{~mA}$ . For $Q_{3}$ and $Q_{4}$ having high $\beta$ values, the current through $R$ and $Q_{4}$ must be $0.5 \mathrm{~mA}$ , thus
$$R=\frac{10-0.7}{0.5}=18.6 \mathrm{k} \Omega$$
(b)
$$R_{C}=\frac{5-3}{0.25}=8 \mathrm{k} \Omega$$
(c)
$$\begin{aligned}v_{I C M \max } & =V_{C 1,2}+0.4 \\& =3.4 \mathrm{~V} \\v_{I C M \min } & =-5+0.3+0.7=-4 \mathrm{~V}\end{aligned}$$
Thus,
$$-4 \mathrm{~V} \leq v_{I C M} \leq+3.4 \mathrm{~V}$$
(d)
$$\frac{v_{o}}{v_{i d}}=g_{m 1,2} R_{C}$$
where
$$g_{m 1,2}=\frac{I_{C 1,2}}{V_{T}}=\frac{0.25 \mathrm{~mA}}{0.025 \mathrm{~V}}=10 \mathrm{~mA} / \mathrm{V}$$
Thus,
$$\frac{v_{o}}{v_{i d}}=10 \times 8=80 \mathrm{~V} / \mathrm{V}$$
(e)
$$\begin{aligned}R_{i d} & =2 r_{\pi}=2 \frac{\beta}{g_{m}} \\& =\frac{2 \times 100}{10}=20 \mathrm{k} \Omega\end{aligned}$$
(f) To raise $R_{i d}$ by a factor of 5 , we include a resistance $R_{E}$ in each of the emitters of $Q_{1}$ and $Q_{2}$ with $R_{E}$ given by
$$\begin{aligned}R_{E} & =4 r_{e} \\& =4 \frac{V_{T}}{I_{E}} \\& =4 \frac{25 \mathrm{mV}}{0.25 \mathrm{~mA}} \\& =400 \Omega\end{aligned}$$
This will reduce the differential gain by the same factor of 5 , thus
$$\frac{v_{o}}{v_{i d}}=\frac{80}{5}=16 \mathrm{~V} / \mathrm{V}$$
(g)
$$\left|A_{c m}\right|=\left(\frac{R_{C}}{2 R_{E E}}\right)\left(\frac{\triangle R_{C}}{R_{C}}\right)$$
where
$$R_{E E}=\left.r_{o}\right|_{Q_{3}}=\frac{V_{A}}{I_{C 3}}=\frac{50}{0.5}=100 \mathrm{k} \Omega$$
$$\frac{\triangle R_{C}}{R_{C}}=0.02$$
Thus,
$$\begin{aligned}\left|A_{c m}\right| & =\frac{8}{2 \times 100} \times 0.02=8 \times 10^{-4} \mathrm{~V} / \mathrm{V} \\\mathrm{CMRR} & =\frac{80}{8 \times 10^{-4}}=10^{5}\end{aligned}$$
or $100 \mathrm{~dB}$ .
(h)
$$\begin{aligned}\left|V_{O}\right| & =0.25\left(R_{C}+0.01 R_{C}\right)-0.25\left(R_{C}-0.01 R_{C}\right) \\& =0.25 \times 0.02 \times 8=0.04 \mathrm{~V} \\& =40 \mathrm{mV} \\V_{O S} & =\frac{40}{80}=0.5 \mathrm{mV}\end{aligned}$$

Question 4

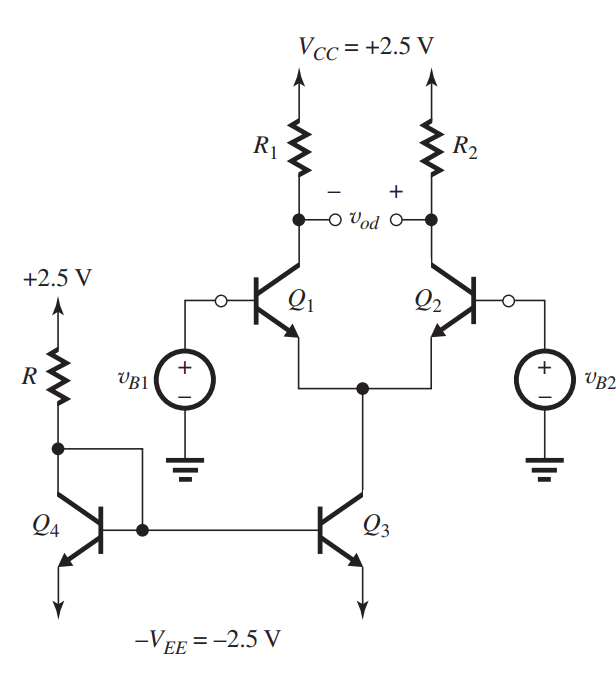
Figure 9.4.1
For the circuit shown in Fig. 9.4.1, neglect base currents in dc calculations and assume that for each transistor $V_{B E}=0.7 \mathrm{~V}$ . Transistors $Q_{1}$ and $Q_{2}$ are perfectly matched. Transistor $Q_{3}$ has twice the emitter-base junction area of $Q_{4}$ .
(a) For $v_{B 1}=v_{B 2}=0 \mathrm{~V}$ , design the circuit to establish a dc bias current of $0.1 \mathrm{~mA}$ in the collector of each of $Q_{1}$ and $Q_{2}$ and a dc voltage of $+1 \mathrm{~V}$ at the collector of each of $Q_{1}$ and $Q_{2}$ . Specify the values required for $R, R_{1}$ , and $R_{2}$ .
(b) For $v_{B 1}=v_{i d} / 2$ and $v_{B 2}=-v_{i d} / 2$ , determine the differential small-signal voltage gain $v_{o d} / v_{i d}$ . Ignore the Early effect. If $\beta_{1}=\beta_{2}=100$ , what is the differential input resistance of the differential amplifier $Q_{1}-Q_{2}$ ?
(c) If $Q_{3}$ has an Early voltage of $100 \mathrm{~V}$ , find its output resistance and use this result to determine the common-mode gain of the differential amplifier $v_{o d} / v_{i c m}$ , where $v_{B 1}=v_{B 2}=v_{i c m}$ and assuming that each of $R_{1}$ and $R_{2}$ is accurate to within $\pm 1 \%$ . What is the resulting CMRR in decibels?

Question 5

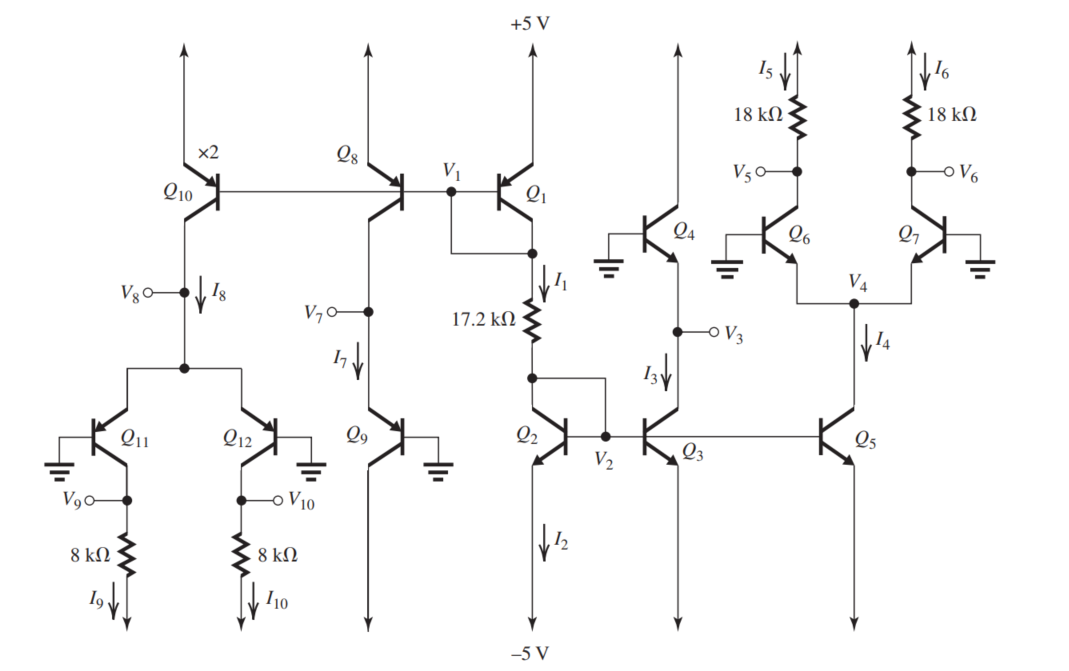
Figure 9.5.1
(a) For the circuit in Fig. 9.5.1 (refer to Figure above), assuming $\left|V_{B E}\right|=0.7 \mathrm{~V}, \beta=\infty$ (i.e., ignoring base currents), and $V_{A}=\infty$ (i.e., ignoring the Early effect), find the dc values of the labelled currents and voltages.
(b) If the bases of $Q_{6}$ and $Q_{7}$ are disconnected from ground and a differential input signal $v_{i d}$ is applied, find the differential gain if the output is taken between the two collectors.
(c) Repeat (b) for the differential amplifier $\left(Q_{11}, Q_{12}\right)$ .

Question 6

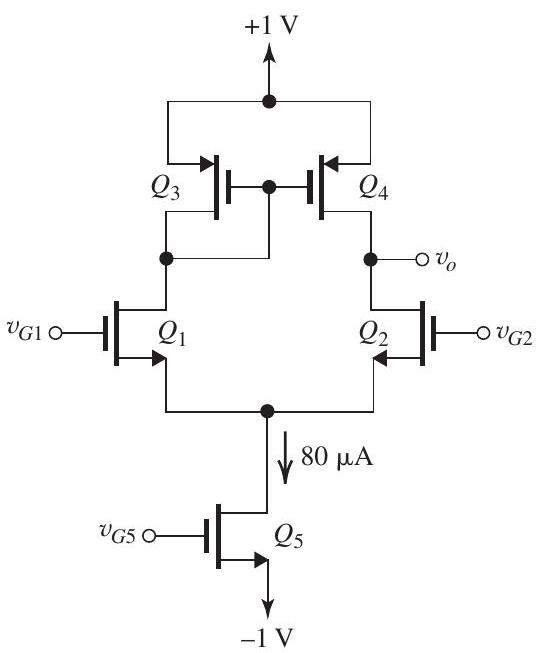
Figure 9.6.1
In the circuit of Fig. 9.6.1, all transistors are matched with $k_{n}=k_{p}=2 \mathrm{~mA} / \mathrm{V}^{2},\left|V_{t}\right|=0.4 \mathrm{~V}$ , and $\left|V_{A}\right|=10 \mathrm{~V}$ .
(a) If $v_{G 1}=v_{G 2}=0 \mathrm{~V}$ , find the dc bias current in each of the four transistors $Q_{1}, Q_{2}, Q_{3}$ , and $Q_{4}$ , as well as the overdrive voltage $\left|V_{O V}\right|$ for each. Ignore the Early effect. Also, find the de voltage at the sources of $Q_{1}$ and $Q_{2}$ , as well as the de voltage at the gates of $Q_{3}$ and $Q_{4}$ .
(b) Find $g_{m}$ of each of $Q_{1}$ and $Q_{2}$ , and determine $r_{o}$ of each of $Q_{2}$ and $Q_{4}$ .
(c) If $v_{G 1}=+v_{i d} / 2$ and $v_{G 2}=-v_{i d} / 2$ , find the differential gain $A_{d}=v_{o} / v_{i d}$ .
(d) Find the output resistance $R_{S S}$ of the biascurrent source $Q_{5}$ and use it to determine the common mode gain $A_{c m}$ in the case $v_{G 1}=v_{G 2}=$ $v_{i \mathrm{~cm}}$ . Also, find the CMRR in $\mathrm{dB}$ .
(e) If it is required to increase the CMRR by $6 \mathrm{~dB}$ , by what factor should the channel length of $Q_{5}$ be changed?

Question 7

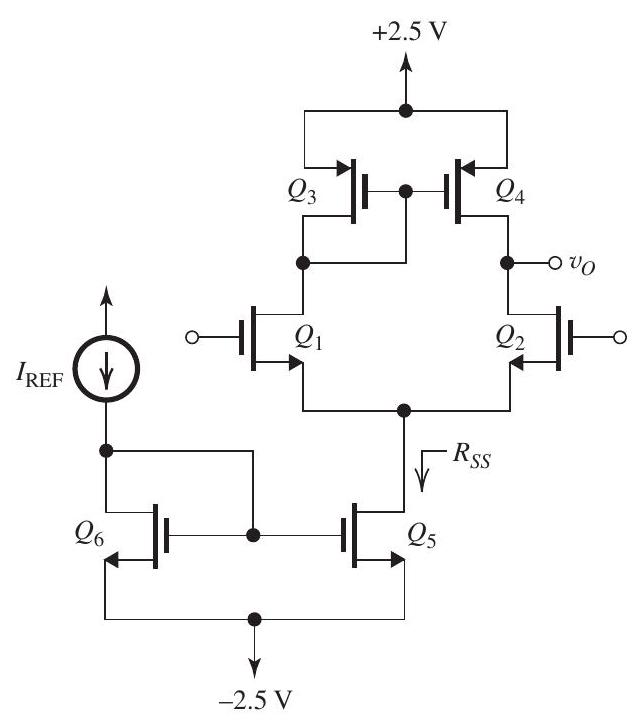
Figure 9.7.1
The current-mirror-loaded CMOS amplifier shown in Fig. 9.7.1 is fabricated in a $0.5-\mu \mathrm{m}$ technology for which $V_{t n}=-V_{t p}=0.5 \mathrm{~V},\left|V_{A}\right|=20 \mathrm{~V}$ , and $\mu_{n} C_{o x}=2 \mu_{p} C_{o x}=200 \mu \mathrm{A} / \mathrm{V}^{2}$ . Transistors $Q_{1}$ and $Q_{2}$ are matched, $Q_{3}$ and $Q_{4}$ are matched, and $Q_{5}$ and $Q_{6}$ are matched. The $(W / L)$ ratios of all devices are selected so that all operate at the same $\left|V_{O V}\right|$ .
(a) Starting from
$$\left|A_{d}\right|=g_{m 1}\left(r_{o 2} \| r_{o 4}\right)$$
and
$$\left|A_{c m}\right|=1 / 2 g_{m 3} R_{S S}$$
show that
$$\left|A_{d}\right|=\left|V_{A}\right| /\left|V_{O V}\right|$$
and
$$\mathrm{CMRR}=2\left(\left|V_{A}\right| /\left|V_{O V}\right|\right)^{2}$$
(b) To obtain a differential gain of $40 \mathrm{~V} / \mathrm{V}$ , find the overdrive voltage $\left|V_{O V}\right|$ at which the transistors should be operated. Also, find the resulting CMRR in $\mathrm{dB}$ .
(c) Using a reference current $I_{\mathrm{REF}}=200 \mu \mathrm{A}$ , find the $(W / L)$ required for each of the six transistors.
(d) With both input terminals grounded, what dc voltage occurs at the output (neglecting the Early effect)? Hence, compute the systematic input offset voltage.
(e) Find the input common-mode range.
(f) If the input differential signal is riding on an input common-mode voltage of $0 \mathrm{~V}$ , what is the maximum allowable output voltage swing in both directions? Hence, find the peak-to-peak amplitude of the largest sine-wave signal that can be applied between the two input terminals (without dc offset compensation).

Question 8

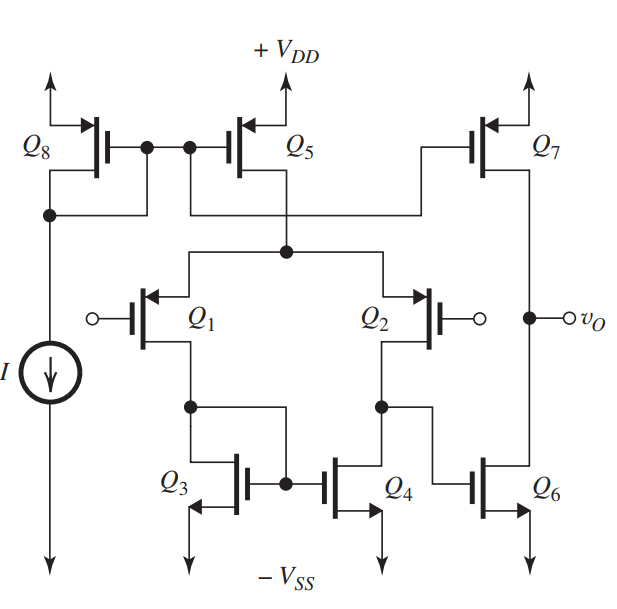
Figure 9.8.1
The two-stage CMOS op amp shown in Fig. 9.8.1 utilizes eight transistors, $Q_{1}$ to $Q_{8}$ , all having the same channel length $L$ . Transistors $Q_{1}$ and $Q_{2}$ are matched and $Q_{3}$ and $Q_{4}$ are matched. For the process technology utilized, $\mu_{n}=4 \mu_{p}$ . All transistors have the same Early voltage, $\left|V_{A}\right|$ .
(a) If the width of each of $Q_{1}$ and $Q_{2}$ is denoted $W$ , find the width of each of $Q_{3}$ to $Q_{8}$ in terms of $W$ so that all transistors operate at equal overdrive voltages, and that $Q_{6}$ conducts a de bias current equal to that supplied by $Q_{7}$ . Neglect the Early effect for this part.
(b) Derive an expression for the overall voltage gain in terms of $\left|V_{A}\right|$ and $\left|V_{O V}\right|$ . Hence, determine the required value of $\left|V_{O V}\right|$ for the case $\left|V_{A}\right|=10$ $\mathrm{V}$ and the voltage gain required is $2500 \mathrm{~V} / \mathrm{V}$ .

Question 9

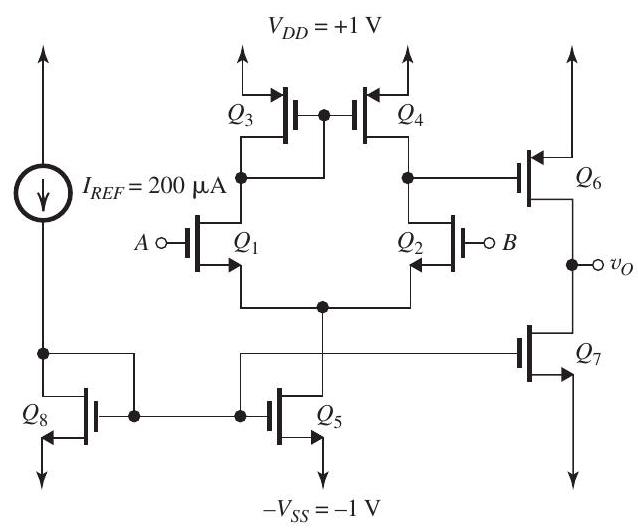
Figure 9.9.1
The two-stage CMOS op amp shown in Fig. 9.9.1 is fabricated in a $0.18-\mu \mathrm{m}$ technology having $k_{n}^{\prime}=$ $4 k_{p}^{\prime}=400 \mu \mathrm{A} / \mathrm{V}^{2}$ , and $V_{t n}=-V_{t p}=0.4 \mathrm{~V}$ .
(a) With $A$ and $B$ grounded, perform a de design that will result in each of $Q_{1}, Q_{2}, Q_{3}$ , and $Q_{4}$ conducting a drain current of $100 \mu \mathrm{A}$ , and each of $Q_{5}, Q_{6}$ , and $Q_{7}$ conducting a drain current of $200 \mu \mathrm{A}$ . Design so that all transistors operate at a $0.2-\mathrm{V}$ overdrive voltage. Neglect the Early effect. Specify the $W / L$ ratio required for each MOSFET.
Present your results in a table. What is the dc voltage at the output (ideally)?
(b) Find the input common-mode range.
(c) Find the allowable range of the output voltage.
(d) With $v_{A}=v_{i d} / 2$ and $v_{B}=-v_{i d} / 2$ , find the voltage gain $v_{O} / v_{i d}$ . Assume that the Early voltage is $\left|V_{A}\right|=5 \mathrm{~V}$ .

Question 10

Refer to Figure 9.10.1 below.


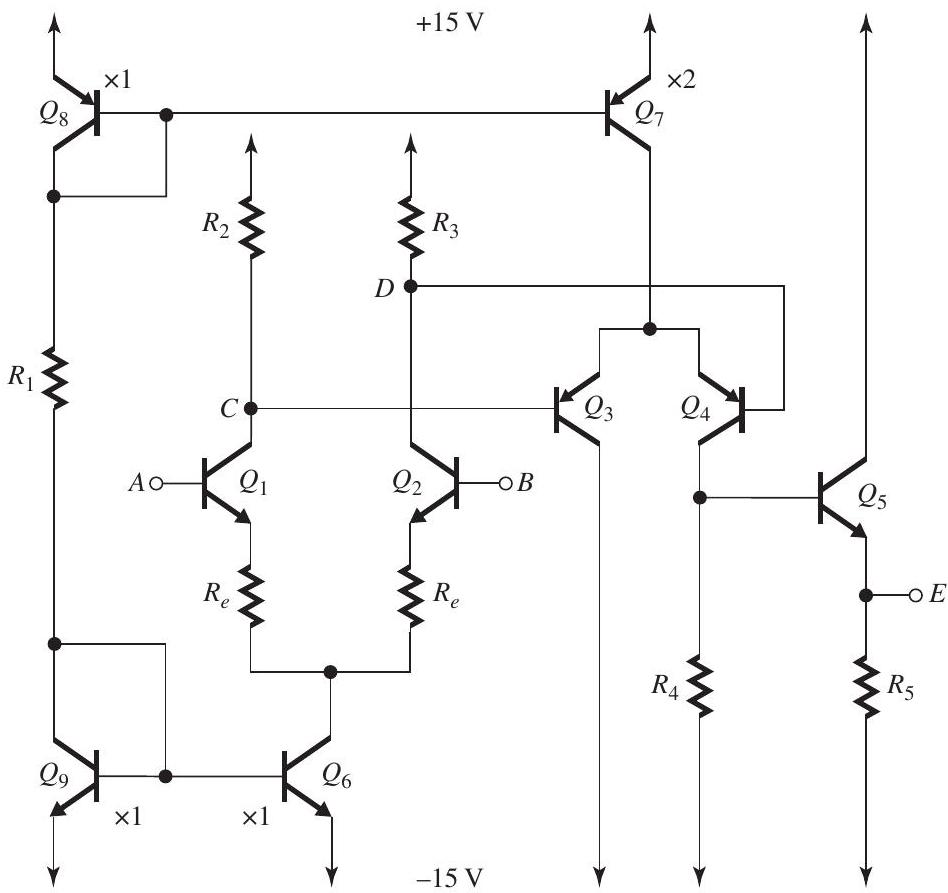
Figure 9.10.1
Note: Neglect the Early effect; that is, assume $r_{O}=\infty$ . Assume $\left|V_{B E}\right|=0.7 \mathrm{~V}$ .
(a) For $V_{A}=V_{B}=0 \mathrm{~V}$ and neglecting all base currents, design the circuit of Fig. 9.10.1 so that each of $Q_{1}$ and $Q_{2}$ operates at a dc bias current of $0.25 \mathrm{~mA}, V_{C}=V_{D}=+10 \mathrm{~V}, V_{E}=0 \mathrm{~V}$ , and $Q_{5}$ operates at a dc bias current of $3 \mathrm{~mA}$ . Specify the dc bias current at which each of $Q_{3}$ and $Q_{4}$ will be operating and give the required value of $R_{1}, R_{2}$ , $R_{3}, R_{4}$ , and $R_{5}$ .
(b) If $\beta=99$ , what must the value of each of the two resistances labeled $R_{e}$ be so as to obtain an input differential resistance of $40 \mathrm{k} \Omega$ ?
(c) Find the differential voltage gain of the input stage, $Q_{1}-Q_{2}$ .
(d) Find the voltage gain of the second stage, $Q_{3}-Q_{4}$ .
(e) Find the voltage gain of the output stage, $Q_{5}$ .
(f) Find the overall voltage gain, $v_{e} /\left(v_{b}-v_{a}\right)$ .