Deck 13: Recursion

Question 1

One reason modular programming is encouraged is that it is an efficient way to manage computer memory.

Answer 1

True

Question 2

Because variables declared in a module are local, and arguments passed by value are copied into local variables, a module can run like an independent program.

Answer 2

True

Question 3

Variables declared in a module are also available to other modules.

Answer 3

False

Question 4

The factorial of a number is the product of all positive integers from that number down to 1.

Question 5

Any recursive procedure can be described nonrecursively.

Question 6

The following algorithm defines a nonrecursive Fibonacci function:

Function Numeric factorial(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index

// Loop
For index = num to 1 Step -1
fact = fact * index
End For
Return fact
End Function

Question 7

The factorial of 4 is the same as 4 times the factorial of 3.

Question 8

The factorial of 3 is the same as 2 times the factorial of 2.

Question 9

The factorial of 7 is 504.

Question 10

The factorial of 6 is 720.

Question 11

A factorial can be defined as factorial(n) = n * factorial(n - 1), with factorial(1) defined as 1.

Question 12

The Fibonacci number at any position (after the first two numbers in the sequence) is the sum of the Fibonacci number at two positions before the current one and the Fibonacci number at one position before the current one.

Question 13

For any integer n greater than or equal to 2, you can represent its position in the Fibonacci sequence, starting the position numbering at 0, as follows:
fibonacci(n) = fibonacci(n - 2) + fibonacci(n - 1)

Question 14

The Fibonacci sequence was mentioned in the 2006 movie The DaVinci Code.

Question 15

For any positive number n, the sum of squares equals 1² + 2² + 3², and so on up to n².

Question 16

The sum of squares of 3 and 5 is 24.

Question 17

The sum of squares of -3 and -8 is 72.

Question 18

Legend says that when the Towers of Hanoi puzzle is completed, the world will come to an end.

Question 19

The Towers of Hanoi puzzle is attributed to the French mathematician Edouard Lucas and is based on a legend about a temple in Vietnam, with 64 golden discs stacked on three posts.

Question 20

The Towers of Hanoi puzzle can be solved with recursion.

Question 21

The greatest common denominator (GCD) of two numbers is the largest integer that can be divided by both numbers evenly (with no remainder).

Question 22

The mathematician Euclid discovered a method for computing the GCD.

Question 23

The greatest common denominator of 79 and 51 is 3.

Question 24

The greatest common denominator of 62 and 22 is 1.

Question 25

Constructor functions cannot be called recursively.

Question 26

____ is a process in which a module calls itself.

A) Stack overflow
B) Short-circuit evaluation
C) Recursion
D) Garbage collection

Question 27

To prevent a neverending recursion process, you must make sure to build a(n) ____ into the procedure.

A) base case
B) sentinel
C) index
D) constructor

Question 28

A(n) ____ is an event that does not call itself and must be reached eventually.

A) base case
B) sentinel
C) index
D) constructor

Question 29

A program's main module occupies a designated place in memory called the ____.

A) branch
B) stub
C) stack
D) base

Question 30

A memory stack contains the main program, and when another module is running, it is said to be placed, or ____ the memory stack until it is finished executing.

A) deposited onto
B) pushed onto
C) withdrawn from
D) popped from

Question 31

____ occurs if a recursive procedure contains no base case.

A) Field testing
B) Housekeeping
C) Stack overflow
D) Data hiding

Question 32

5! * 5! is ____.

A) 120
B) 720
C) 5040
D) 14400

Question 33

6! / (2! * 4!) = ____.

A) 2
B) 15
C) 24
D) 32

Question 34

4!/0! = ____.

A) 2
B) 15
C) 24
D) 32

Question 35

(10! / 5!) / 10 = ____.

A) 720
B) 1440
C) 3024
D) 5040

Question 36

Which of the following represents the factorial function?

A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function

B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function

C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function

D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Question 37

The following sequence is known as the ____.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

A) sum of squares
B) Towers of Hanoi
C) Fibonacci sequence
D) factorial sequence

Question 38

Which of the following represents the Fibonnacci sequence?

A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function

B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function

C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1 // factorial result
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function

D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Question 39

Which of the following represents the sum of squares?

A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function

B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function

C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function

D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Question 40

The sum of squares of -5 and -7 is ____.

A) 28
B) 74
C) 82
D) 94

Question 41

The sum of squares of the first two even integers is ____.

A) 5
B) 10
C) 15
D) 20

Question 42

The sum of squares can be defined as ____.

A) (num) + sumOfSquares(num - 1)
B) (num / num) + sumOfSquares(num - 1)
C) (num * num) + sumOfSquares(num - 1)
D) (num * num) + sumOfSquares(num)

Question 43

Which of the following is played with three pegs and a stack of discs?

A) The Towers of Hanoi
B) Chess
C) The sum of squares
D) Checkers

Question 44

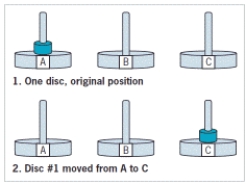
-The accompanying figure represents the ____.

A) Towers of Hanoi
B) Fibonacci sequence
C) sum of squares
D) factorial sequence

Question 45

Which of the following represents the Towers of Hanoi?

A) Function Numeric unKnown(Numeric num)
// Call function recursively until reaching 0 or 1
If num == 0 Or num == 1 Then
Return num
Else
Return unKnown(num - 2) + unKnown(num - 1)
End If
End Function

B) Function Numeric unKnown(Numeric num)
// Base case returns 1
If (num == 1) Then
Return 1
Else
Return (num * num) + unKnown(num - 1)
End If
End Function

C) Function Numeric unKnown(Numeric num)
// Declare variables
Declare Numeric fact = 1
Declare Numeric index // loop index
// Loop
For index = num to 1 Step -1
Fact = fact * index
End For
Return fact
End Function

D) Module unKnown(Integer n, sourcePeg, targetPeg, sparePeg)
If (n > 0) Then
MoveDiscs(n - 1, sourcePeg, sparePeg, targetPeg)
// Move disc from sourcePeg to targetPeg
MoveDiscs(n - 1, sparePeg, targetPeg, sourcePeg)
End If
End Module

Question 46

What is the greatest common denominator of 30 and 36?

A) 1
B) 2
C) 4
D) 6

Question 47

What is the greatest common denominator of 87 and 41?

A) 1
B) 2
C) 4
D) 6

Question 48

What is the greatest common denominator of 36 and 22?

A) 1
B) 2
C) 4
D) 6

Question 49

What is the greatest common denominator of 105 and 35?

A) 5
B) 15
C) 25
D) 35

Question 50

The following algorithm represents the ____.
Function Numeric unKnown(Numeric x, Numeric y)
If y = 0 Then
Return x
Else
Return GCD(y, x % y)
End If
End Function

A) sum of squares
B) Fibonacci series
C) GCD function
D) factorial series