Deck 14: Using Designs With More Than One Independent Variable and Two-Way Between-Subjects Anova
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/13
العب
ملء الشاشة (f)
Deck 14: Using Designs With More Than One Independent Variable and Two-Way Between-Subjects Anova
1
In a two-way factorial ANOVA, the formula for calculating SSTotal is:
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
2
In a two-way factorial ANOVA, the formula for calculating SSFactor A is:
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
3
In a two-way factorial ANOVA, the formula for calculating SSFactor B is:
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .
.
4
In a two-way factorial ANOVA, the formula for calculating SSA×B is:
A) .
B)
C) .
D) .
A) .
B)
C) .
D) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
5
In a two-way factorial ANOVA, the formula for calculating SSError is:
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
6
In a study with three levels of factor A, three levels of factor B, and 6 subjects in each condition, dfA and dfB would be _____ and _____, respectively.
A) 3; 3
B) 2; 3
C) 3; 2
D) 2; 2
A) 3; 3
B) 2; 3
C) 3; 2
D) 2; 2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
7
In a study with three levels of factor A, three levels of factor B, and 6 subjects in each condition, the dfAxB would be:
A) 9.
B) 6.
C) 4.
D) 3.
A) 9.
B) 6.
C) 4.
D) 3.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
8
A two-way ANOVA has _____, and a three-way ANOVA has _____.
A) two independent variables; three dependent variables
B) two dependent variables; three dependent variables
C) two independent variables; three independent variables
D) two dependent variables; three independent variables
A) two independent variables; three dependent variables
B) two dependent variables; three dependent variables
C) two independent variables; three independent variables
D) two dependent variables; three independent variables

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
9
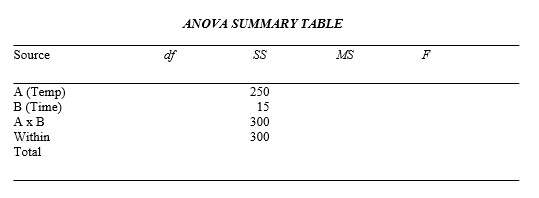
The following ANOVA table corresponds to an experiment with two IV's; 1) Time of Day (Morning or Afternoon) and 2) Room Temperature (Cool, Normal, or Warm). The productivity level (on a 0-100 scale) of employees during the morning or afternoon is measured in either cool, normal, or warm working conditions. This is a completely between-subjects design. The corresponding means for each group are as follows:
Cool Temp/Afternoon - 55
Cool Temp/Morning - 100
Normal Temp/Afternoon - 60
Normal Temp/Morning - 60
Warm Temp/Afternoon - 50
Warm Temp/Morning - 10
Construct the matrix showing the means in each cell, give the factorial notation, fill in the ANOVA table, draw a graph showing the results, calculate Tukey's HSD if appropriate, and draw conclusions concerning this study. There are 10 subjects in each cell (condition).
Cool Temp/Afternoon - 55
Cool Temp/Morning - 100
Normal Temp/Afternoon - 60
Normal Temp/Morning - 60
Warm Temp/Afternoon - 50
Warm Temp/Morning - 10
Construct the matrix showing the means in each cell, give the factorial notation, fill in the ANOVA table, draw a graph showing the results, calculate Tukey's HSD if appropriate, and draw conclusions concerning this study. There are 10 subjects in each cell (condition).


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
10
An experiment with two variables each with three levels is a _____ factorial design.
A) 3 × 3
B) 2 × 2
C) 2 × 2 × 2
D) 3 × 3 × 3
A) 3 × 3
B) 2 × 2
C) 2 × 2 × 2
D) 3 × 3 × 3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
11
An experiment with four variables each with two levels is a _____ factorial design.
A) 2 × 4
B) 2 × 2
C) 2 × 2 × 2 × 2
D) 2 × 3 × 4
A) 2 × 4
B) 2 × 2
C) 2 × 2 × 2 × 2
D) 2 × 3 × 4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
12
When graphed, a significant interaction will definitely have _____.
A) parallel lines
B) nonparallel lines
C) a crossover interaction
D) none of the above
A) parallel lines
B) nonparallel lines
C) a crossover interaction
D) none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck
13
According to the experiment discussed in the text [i.e., 2 IV's: Word Type (Concrete vs. Abstract) and Rehearsal Type (Elaborative vs. Rote) and one DV: % of words recalled correctly], show the graph for the experimental results of NO main effect of rehearsal, NO interaction effect, and NO main effect of Word Type. Hint: First, construct a matrix of what you think the cell means should be. It might help you.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 13 في هذه المجموعة.
فتح الحزمة
k this deck








