Deck 10: Nonlinear Optimization Models
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/60
العب
ملء الشاشة (f)
Deck 10: Nonlinear Optimization Models
1
A feasible solution is _____ if there are no other feasible points with a smaller objective function value in the entire feasible region.
A) a global minimum
B) not a local maximum
C) not a local minimum
D) bowl-shaped
A) a global minimum
B) not a local maximum
C) not a local minimum
D) bowl-shaped
a global minimum
2
A global minimum
A) is also a local maximum.
B) need not be a local maximum, but vice versa is true.
C) is also a local minimum.
D) need not be local minimum, but vice versa is true.
A) is also a local maximum.
B) need not be a local maximum, but vice versa is true.
C) is also a local minimum.
D) need not be local minimum, but vice versa is true.
is also a local minimum.
3
If all the squared terms in a quadratic function have a negative coefficient and there are no cross-product terms, then the function is a _____ function.
A) convex quadratic
B) nonlinear objective
C) concave quadratic
D) negative elliptical
A) convex quadratic
B) nonlinear objective
C) concave quadratic
D) negative elliptical
concave quadratic
4
If there are no other feasible points with a larger objective function value in the entire feasible region, a feasible solution is _____.
A) an efficient frontier
B) a global maximum
C) not a local maximum
D) a global minimum
A) an efficient frontier
B) a global maximum
C) not a local maximum
D) a global minimum

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
5
A _____ is the shadow price of a binding simple lower or upper bound on the decision variable.
A) reduced gradient
B) binding constraint
C) binary variable
D) local optimum
A) reduced gradient
B) binding constraint
C) binary variable
D) local optimum

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
6
A nonlinear function with term to the power of two is known as a _____.
A) hyperbolic function
B) quadratic function
C) logarithmic function
D) cubic function
A) hyperbolic function
B) quadratic function
C) logarithmic function
D) cubic function

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
7
Reference - 10.2: Use the graph given below to answer questions

Reference - 10.2. Which of the following functions is most likely to yield the above shape?
A) f(X, Y) = x₂ + y₂
B) f(X, Y) = Xsin(2?πY) + Ysin(2πX)
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

Reference - 10.2. Which of the following functions is most likely to yield the above shape?
A) f(X, Y) = x₂ + y₂
B) f(X, Y) = Xsin(2?πY) + Ysin(2πX)
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
8
If there are no other feasible solutions with a larger objective function value in the immediate neighborhood, then the feasible solution is known as _____.
A) a global maximum
B) infeasible
C) a nonlinear solution
D) a local maximum
A) a global maximum
B) infeasible
C) a nonlinear solution
D) a local maximum

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
9
In a nonlinear optimization problem:
A) the objective function is a nonlinear function of the constraints.
B) all the constraints are nonlinear only when the objective is to maximize the function of the decision variables.
C) at least one term in the objective function or a constraint is nonlinear.
D) both the objective function and the constraints must have all nonlinear terms.
A) the objective function is a nonlinear function of the constraints.
B) all the constraints are nonlinear only when the objective is to maximize the function of the decision variables.
C) at least one term in the objective function or a constraint is nonlinear.
D) both the objective function and the constraints must have all nonlinear terms.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
10
In a nonlinear problem, the rate of change of the objective function with respect to the right-hand side of a constraint is given by the ____.
A) slope of the contour line
B) local optimum
C) Reducing gradient
D) Lagrangian multiplier
A) slope of the contour line
B) local optimum
C) Reducing gradient
D) Lagrangian multiplier

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
11
The _____ of a solution is a mathematical concept that refers to the set of points within a relatively close proximity of the solution.
A) objective function contour
B) neighborhood
C) regression equation
D) Lagrangian multiplier
A) objective function contour
B) neighborhood
C) regression equation
D) Lagrangian multiplier

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
12
The Lagrangian multiplier is the _____ for a constraint in a nonlinear problem.
A) shadow price
B) payoff value
C) reducing gradient
D) reduced cost
A) shadow price
B) payoff value
C) reducing gradient
D) reduced cost

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
13
A function that is bowl-shaped down is called a _____ function.
A) concave
B) convex
C) conic
D) linear
A) concave
B) convex
C) conic
D) linear

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
14
A feasible solution is a local minimum if there are no other feasible solutions with a:
A) smaller objective function value in the immediate neighborhood.
B) same objective function value in the immediate neighborhood.
C) set of points defining the minimum possible risk in the entire feasible region.
D) same objective function value in the entire feasible region.
A) smaller objective function value in the immediate neighborhood.
B) same objective function value in the immediate neighborhood.
C) set of points defining the minimum possible risk in the entire feasible region.
D) same objective function value in the entire feasible region.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
15
The reduced gradient is analogous to the _____ for linear models.
A) binary variable
B) binding constraint
C) reduced cost
D) objective coefficient
A) binary variable
B) binding constraint
C) reduced cost
D) objective coefficient

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
16
A feasible solution is _____ if there are no other feasible points with a better objective function value in the entire feasible region.
A) infeasible
B) unbounded
C) nonlinear
D) a global optimum
A) infeasible
B) unbounded
C) nonlinear
D) a global optimum

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
17
Reference - 10.1: Use the graph given below to answer questions
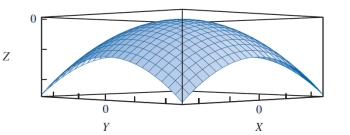
Reference - 10.1. The point (0, 0) is a(n) _____ for the given concave function.
A) local maximum
B) local minimum
C) convergence point
D) endpoint

Reference - 10.1. The point (0, 0) is a(n) _____ for the given concave function.
A) local maximum
B) local minimum
C) convergence point
D) endpoint

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
18
A function that is bowl-shaped up is called a(n) _____ function.
A) concave
B) optimal
C) convex
D) elliptical
A) concave
B) optimal
C) convex
D) elliptical

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
19
Reference - 10.1: Use the graph given below to answer questions

Reference - 10.1. Which of the following functions is most likely to yield the above shape?
A) f(X, Y) = x₂ + y₂
B) f(X, Y) = -X - Y
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

Reference - 10.1. Which of the following functions is most likely to yield the above shape?
A) f(X, Y) = x₂ + y₂
B) f(X, Y) = -X - Y
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
20
A feasible solution is a(n) _____ if there are no other feasible solutions with a better objective function value in the immediate neighborhood.
A) efficient frontier
B) local optimum
C) global maximum
D) diverging function
A) efficient frontier
B) local optimum
C) global maximum
D) diverging function

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
21
One of the ways to formulate the Markowitz model is to:
A) maximize the variance of the portfolio subject to a constraint on the expected return of the portfolio.
B) minimize the expected return of the portfolio subject to a constraint on variance.
C) minimize the variance of the portfolio subject to a constraint on the expected return of the portfolio.
D) minimize the expected return of the portfolio with no constraint on variance.
A) maximize the variance of the portfolio subject to a constraint on the expected return of the portfolio.
B) minimize the expected return of the portfolio subject to a constraint on variance.
C) minimize the variance of the portfolio subject to a constraint on the expected return of the portfolio.
D) minimize the expected return of the portfolio with no constraint on variance.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
22
The measure of risk most often associated with the Markowitz portfolio model is the
A) expected return of the portfolio.
B) annual interest on the portfolio.
C) variance of the portfolio's return.
D) number of investments listed in the portfolio.
A) expected return of the portfolio.
B) annual interest on the portfolio.
C) variance of the portfolio's return.
D) number of investments listed in the portfolio.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
23
In the Bass forecasting model, the _____ measures the likelihood of adoption due to a potential adopter being influenced by someone who has already adopted the product.
A) coefficient of innovation
B) coefficient of imitation
C) coefficient of regression
D) coefficient of the objective function
A) coefficient of innovation
B) coefficient of imitation
C) coefficient of regression
D) coefficient of the objective function

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
24
In the Bass forecasting model, the _____ measures the likelihood of adoption, assuming no influence from someone who has already purchased (adopted) the product.
A) coefficient of correlation
B) coefficient of imitation
C) coefficient of independence
D) coefficient of innovation
A) coefficient of correlation
B) coefficient of imitation
C) coefficient of independence
D) coefficient of innovation

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
25
One of the ways to use the Bass forecasting model is to wait until several periods of data for the problem under consideration are available. This is known as the _____ approach.
A) branch-and-bound
B) cutting plane
C) rolling-horizon
D) sensible-period
A) branch-and-bound
B) cutting plane
C) rolling-horizon
D) sensible-period

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
26
Reference - 10.3: Use the graph given below to answer questions
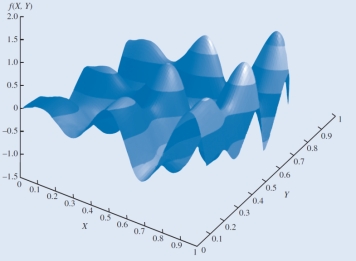
Reference - 10.3. Which of the following equations is most likely to yield the above curve?
A) f(X, Y) = Xlog(2?πY) + Ylog(2πX)
B) f(X, Y) = X - Y
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

Reference - 10.3. Which of the following equations is most likely to yield the above curve?
A) f(X, Y) = Xlog(2?πY) + Ylog(2πX)
B) f(X, Y) = X - Y
C) f(X, Y) = -x₂ - y₂
D) f(X, Y) = Xsin(5?πX) + Ysin(5π?Y)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
27
The _____ option is helpful when the solution to a problem appears to depend on the starting values for the decision variables.
A) Restart
B) Convergence
C) Derivatives
D) Multistart
A) Restart
B) Convergence
C) Derivatives
D) Multistart

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
28
A(n) _____ is a set of points defining the minimum possible risk for a set of return values.
A) Contour
B) Efficient frontier
C) Unity constraint
D) Reduced gradient
A) Contour
B) Efficient frontier
C) Unity constraint
D) Reduced gradient

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
29
Which of the following is a second way of formulating the Markowitz model?
A) Maximizing the expected return of the portfolio subject to a constraint on variance
B) Minimizing the expected return of the portfolio subject to a constraint on variance.
C) Maximizing the variance of the portfolio subject to a constraint on the expected return of the portfolio
D) Maximizing the variance of the portfolio with no constraint needed for the expected return of the portfolio
A) Maximizing the expected return of the portfolio subject to a constraint on variance
B) Minimizing the expected return of the portfolio subject to a constraint on variance.
C) Maximizing the variance of the portfolio subject to a constraint on the expected return of the portfolio
D) Maximizing the variance of the portfolio with no constraint needed for the expected return of the portfolio

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
30
Reference - 10.3: Use the graph given below to answer questions

Reference - 10.3. Which of the following is true of the above function?
A) It has single local minimum.
B) It has multiple local optima.
C) It has single local maximum.
D) It has no maxima and minima.

Reference - 10.3. Which of the following is true of the above function?
A) It has single local minimum.
B) It has multiple local optima.
C) It has single local maximum.
D) It has no maxima and minima.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
31
Excel Solver's _____ is based on a method that searches for an optimal solution by iteratively adjusting a population of candidate solutions.
A) Evolutionary Solver
B) Goal Seeker
C) Simplex LP
D) GRG Nonlinear
A) Evolutionary Solver
B) Goal Seeker
C) Simplex LP
D) GRG Nonlinear

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
32
The portfolio variance is the:
A) sum of the squares of the deviations from the mean value under each scenario.
B) average of the sum of the squares of the deviations from the mean value under each investment scenario.
C) average of the product of the squares of the deviations from the mean value under each scenario.
D) average of the sum of the deviations from the mean value under each investment scenario.
A) sum of the squares of the deviations from the mean value under each scenario.
B) average of the sum of the squares of the deviations from the mean value under each investment scenario.
C) average of the product of the squares of the deviations from the mean value under each scenario.
D) average of the sum of the deviations from the mean value under each investment scenario.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
33
A portfolio optimization model used to construct a portfolio that minimizes risk subject to a constraint requiring a minimum level of return is known as_____.
A) capital budgeting pricing model
B) market share optimization model
C) Hauck maximum variance portfolio model
D) Markowitz mean-variance portfolio model
A) capital budgeting pricing model
B) market share optimization model
C) Hauck maximum variance portfolio model
D) Markowitz mean-variance portfolio model

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
34
Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: Ft = (p + q[Ct - ₁ /m]) (m - Ct - ₁),
Where m = the number of people estimated to eventually adopt the new product,
Ct - ₁ = the number of people who have adopted the product through time t - 1,
Q = the coefficient of imitation, and
P = the coefficient of innovation.)
![<strong>Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: Ft = (p + q[Ct - ₁ /m]) (m - Ct - ₁), Where m = the number of people estimated to eventually adopt the new product, Ct - ₁ = the number of people who have adopted the product through time t - 1, Q = the coefficient of imitation, and P = the coefficient of innovation.) </strong> A) q < p B) q > p C) m < q D) p > m](https://d2lvgg3v3hfg70.cloudfront.net/TB1880/11ea4021_0f0f_718b_b5a8_5175fdb9a7ea_TB1880_00.jpg)
A) q < p
B) q > p
C) m < q
D) p > m
Where m = the number of people estimated to eventually adopt the new product,
Ct - ₁ = the number of people who have adopted the product through time t - 1,
Q = the coefficient of imitation, and
P = the coefficient of innovation.)
![<strong>Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: Ft = (p + q[Ct - ₁ /m]) (m - Ct - ₁), Where m = the number of people estimated to eventually adopt the new product, Ct - ₁ = the number of people who have adopted the product through time t - 1, Q = the coefficient of imitation, and P = the coefficient of innovation.) </strong> A) q < p B) q > p C) m < q D) p > m](https://d2lvgg3v3hfg70.cloudfront.net/TB1880/11ea4021_0f0f_718b_b5a8_5175fdb9a7ea_TB1880_00.jpg)
A) q < p
B) q > p
C) m < q
D) p > m

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
35
In the Bass forecasting model, parameter m:
A) measures the likelihood of adoption due to a potential adopter being influenced by someone who has already adopted the product.
B) measures the likelihood of adoption, assuming no influence from someone who has already adopted the product.
C) refers to the number of people estimated to eventually adopt the new product.
D) refers to the number of people who have already adopted the new product.
A) measures the likelihood of adoption due to a potential adopter being influenced by someone who has already adopted the product.
B) measures the likelihood of adoption, assuming no influence from someone who has already adopted the product.
C) refers to the number of people estimated to eventually adopt the new product.
D) refers to the number of people who have already adopted the new product.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
36
Reference - 10.3: Use the graph given below to answer questions

Reference - 10.3. The feasible region for the function represented in the graph is:
A) -1 ≤ X ≤ 1, -1 ≤ Y ≤ 1.
B) -1.5 ≤ X ≤ 1, 0 ≤ Y ≤ ∞.
C) -1.5 ≤ X ≤ 2.0, -1.5 ≤ Y ≤ 2.0.
D) 0 ≤ X ≤ 1, 0 ≤ Y ≤ 1.

Reference - 10.3. The feasible region for the function represented in the graph is:
A) -1 ≤ X ≤ 1, -1 ≤ Y ≤ 1.
B) -1.5 ≤ X ≤ 1, 0 ≤ Y ≤ ∞.
C) -1.5 ≤ X ≤ 2.0, -1.5 ≤ Y ≤ 2.0.
D) 0 ≤ X ≤ 1, 0 ≤ Y ≤ 1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
37
Reference - 10.2: Use the graph given below to answer questions

Reference - 10.2. What is the minimum value for this function?
A) -∞
B) 0
C) -1
D) 1

Reference - 10.2. What is the minimum value for this function?
A) -∞
B) 0
C) -1
D) 1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
38
Solving nonlinear problems with local optimal solutions is performed using _____, in Excel Solver, which is based on more classical optimization techniques.
A) Goal Seeker
B) Linear Regression
C) GRG Nonlinear
D) Simplex LP
A) Goal Seeker
B) Linear Regression
C) GRG Nonlinear
D) Simplex LP

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
39
If the portfolio variance were equal to zero, the amount of risk would be _____.
A) unity
B) a positive number greater than 1
C) negative always
D) zero
A) unity
B) a positive number greater than 1
C) negative always
D) zero

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
40
The _____forecasting model uses nonlinear optimization to forecast the adoption of innovative and new technologies in the marketplace.
A) Hauck
B) LMS
C) Markowitz
D) Bass
A) Hauck
B) LMS
C) Markowitz
D) Bass

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
41
Roger is willing to promote and sell two types of smart watches, X and Y, at his outlet. The demand for these two watches are as follows:
DX = -0.45PX + 0.34PY + 242
DY = 0.2PX - 0.58PY + 282
where, DX is the demand for watch X, PX is the selling price of watch X, DY is the demand for watch Y, and PY is the selling price of watch Y.
Rogers wishes to determine the selling price that maximizes revenue for these two products. Develop the revenue function for these two models, and find the revenue maximizing prices.
DX = -0.45PX + 0.34PY + 242
DY = 0.2PX - 0.58PY + 282
where, DX is the demand for watch X, PX is the selling price of watch X, DY is the demand for watch Y, and PY is the selling price of watch Y.
Rogers wishes to determine the selling price that maximizes revenue for these two products. Develop the revenue function for these two models, and find the revenue maximizing prices.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
42
Consider the following data on the returns from bonds:
 Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.
Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.
 Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.
Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
43
Consider the return scenario for 3 types of mutual funds, shown in the following table:
 a. Construct the Markowitz model that maximizes expected return subject to a maximum variance of 35.
a. Construct the Markowitz model that maximizes expected return subject to a maximum variance of 35.
b. Solve the model developed in part a. Round all your answers to three decimal places.
 a. Construct the Markowitz model that maximizes expected return subject to a maximum variance of 35.
a. Construct the Markowitz model that maximizes expected return subject to a maximum variance of 35.b. Solve the model developed in part a. Round all your answers to three decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
44
Develop a model that minimizes semivariance for the data given below with a required return of 15 percent. Define a variable ds for each scenario and let ds≥R-Rs with ds ≥ 0. Then make the objective function: Min 14s=14ds2.
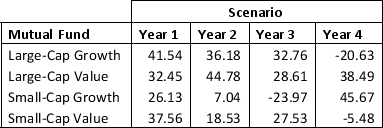
Solve the model you developed with a required expected return of at least 15 percent.

Solve the model you developed with a required expected return of at least 15 percent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
45
Consider the objective function,
where,
Y = total output
A= total-factor productivity
L = labor input
K= capital input
α = capital input share of contribution for L
β = capital input share of contribution for K a. Assume α = 0.33, β = 0.67, A = 10 and each unit of labor costs $45 and each unit of capital costs $55. With $50,000 available in the budget, develop an optimization model to determine the number of units of capital and labor required in order to maximize output.
b. Find the optimal solution to the model you formulated in part a. Round all your answers to two decimal places. (Hint: When using Excel Solver, use the Multistart option with bounds 0 ≤ L ≤ 700 and 0 ≤ K ≤ 1000.)
where,
Y = total output
A= total-factor productivity
L = labor input
K= capital input
α = capital input share of contribution for L
β = capital input share of contribution for K a. Assume α = 0.33, β = 0.67, A = 10 and each unit of labor costs $45 and each unit of capital costs $55. With $50,000 available in the budget, develop an optimization model to determine the number of units of capital and labor required in order to maximize output.
b. Find the optimal solution to the model you formulated in part a. Round all your answers to two decimal places. (Hint: When using Excel Solver, use the Multistart option with bounds 0 ≤ L ≤ 700 and 0 ≤ K ≤ 1000.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
46
Consider the stock return data given below.

Develop and solve the Markowitz model that maximizes expected return subject to a maximum variance of 35. Use this model to construct an efficient frontier by varying the maximum allowable variance from 25 to 55 in increments of 5 and solving for the maximum return for each.

Develop and solve the Markowitz model that maximizes expected return subject to a maximum variance of 35. Use this model to construct an efficient frontier by varying the maximum allowable variance from 25 to 55 in increments of 5 and solving for the maximum return for each.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
47
Jim is trying to solve a problem where the point A should be within the radius of 15cms from points B, C, D, E, and F. The decision variables are defined as below.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below:
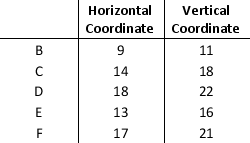
Formulate and solve a model that minimizes the maximum distance from point A to each of the points B, C, D, E, and F. Round all your answers to three decimal places.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below:

Formulate and solve a model that minimizes the maximum distance from point A to each of the points B, C, D, E, and F. Round all your answers to three decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
48
A Steel Manufacturing company has two production facilities that manufacture Dishwashers. Production costs at the two facilities differ because of varying labor costs, local property taxes, type of material used, volume, and so on. For Plant A, the weekly costs for producing a number of units of Dishwashers is expressed as a function:
TCA(X) = X² - 2X + 12000
where X is the weekly production volume and TCA(X) is the weekly cost for Plant A. Plant B's weekly production costs are given by
TCB(Y) = Y² + 8Y + 10000
where Y is the weekly production volume and TCB(Y) is the weekly cost for Plant B. The manufacturer would like to produce 50 dishwashers per week at the lowest possible cost. a. Formulate a mathematical model that can be used to determine the optimal number of dishwashers to produce each week at each facility. a. Solve the optimization model to determine the optimal number of dishwashers to produce at each facility.
TCA(X) = X² - 2X + 12000
where X is the weekly production volume and TCA(X) is the weekly cost for Plant A. Plant B's weekly production costs are given by
TCB(Y) = Y² + 8Y + 10000
where Y is the weekly production volume and TCB(Y) is the weekly cost for Plant B. The manufacturer would like to produce 50 dishwashers per week at the lowest possible cost. a. Formulate a mathematical model that can be used to determine the optimal number of dishwashers to produce each week at each facility. a. Solve the optimization model to determine the optimal number of dishwashers to produce at each facility.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
49
Consider the data on investment made in four types of funds and returns from S&P 500.
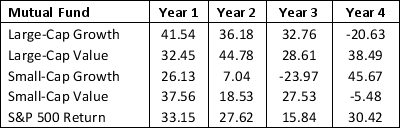 a. Develop an optimization model that will give the fraction of the portfolio to invest in each of the funds so that the return of the resulting portfolio matches as closely as possible the return of the S&P 500 Index. (Hint: Minimize the sum of the squared deviations between the portfolio's return and the S&P 500 Index return for each year in the data set.)
a. Develop an optimization model that will give the fraction of the portfolio to invest in each of the funds so that the return of the resulting portfolio matches as closely as possible the return of the S&P 500 Index. (Hint: Minimize the sum of the squared deviations between the portfolio's return and the S&P 500 Index return for each year in the data set.)
b. Solve the model developed in part a.
 a. Develop an optimization model that will give the fraction of the portfolio to invest in each of the funds so that the return of the resulting portfolio matches as closely as possible the return of the S&P 500 Index. (Hint: Minimize the sum of the squared deviations between the portfolio's return and the S&P 500 Index return for each year in the data set.)
a. Develop an optimization model that will give the fraction of the portfolio to invest in each of the funds so that the return of the resulting portfolio matches as closely as possible the return of the S&P 500 Index. (Hint: Minimize the sum of the squared deviations between the portfolio's return and the S&P 500 Index return for each year in the data set.)b. Solve the model developed in part a.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
50
Gatson manufacturing company is willing to promote 2 types of tires: Economy tire; Premium tire, and these two tires are independent of each other in terms of demand, cost, price, etc. An analytics team of this company has estimated the profit functions for both the tires as,
Monthly profit for Economy tire = 49.2415 LN(XA) + 180.414
Monthly profit for Premium tire = 84.344 LN(XB) - 150.112
where XA and XB are the advertising amount allocated to Economy tire and Premium tire, respectively, and LN is the natural logarithm function. The advertising budget is $200,000, and management has dictated that at least $20,000 must be allocated to each of the two tires.
(Hint: To compute a natural logarithm for the value X in Excel, use the formula =LN(X). For Solver to find an answer, you also need to start with decision variable values greater than 0 in this problem.)
Develop and solve an optimization model that will prescribe how the company should allocate its marketing budget to maximize profit.
Monthly profit for Economy tire = 49.2415 LN(XA) + 180.414
Monthly profit for Premium tire = 84.344 LN(XB) - 150.112
where XA and XB are the advertising amount allocated to Economy tire and Premium tire, respectively, and LN is the natural logarithm function. The advertising budget is $200,000, and management has dictated that at least $20,000 must be allocated to each of the two tires.
(Hint: To compute a natural logarithm for the value X in Excel, use the formula =LN(X). For Solver to find an answer, you also need to start with decision variable values greater than 0 in this problem.)
Develop and solve an optimization model that will prescribe how the company should allocate its marketing budget to maximize profit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
51
Consider the stock return data given below.
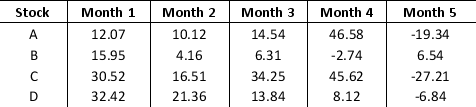 a. Construct the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur.
a. Construct the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur.
b. Solve the model using Excel Solver.
 a. Construct the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur.
a. Construct the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur.b. Solve the model using Excel Solver.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
52
The profit function for two types of iPod is :
where x₁ and x₂ represent number of units of production of basic and advanced iPods, respectively.
Production time required for the basic iPod is 6 hours per unit, and production time required for the advanced iPod is 8 hours per unit. Currently, 50 hours are available. The cost of hours is already factored into the profit function. a. Formulate an optimization problem that can be used to find the optimal production quantity of basic and advanced iPods.
b. Solve the optimization model you formulated in part a. How much should be produced?
where x₁ and x₂ represent number of units of production of basic and advanced iPods, respectively.
Production time required for the basic iPod is 6 hours per unit, and production time required for the advanced iPod is 8 hours per unit. Currently, 50 hours are available. The cost of hours is already factored into the profit function. a. Formulate an optimization problem that can be used to find the optimal production quantity of basic and advanced iPods.
b. Solve the optimization model you formulated in part a. How much should be produced?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
53
The manager of a supermarket estimates the average number of trips made to the warehouse from each of the 5 outlets and he wants the warehouse to be closer to the outlets which has high number of average trips. The available data on the distance between the warehouse and the outlets are provided in terms of horizontal and vertical distances. That is, X = horizontal coordinate of the warehouse; and Y = vertical coordinate of the warehouse. The data is shown below.
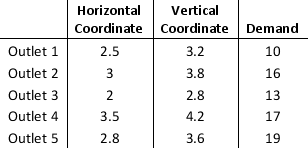 a. Develop a new unconstrained model that minimizes the sum of the demand-weighted distance defined as the product of the demand (measured in number of trips) and the distance to the warehouse.
a. Develop a new unconstrained model that minimizes the sum of the demand-weighted distance defined as the product of the demand (measured in number of trips) and the distance to the warehouse.
b. Solve the model you developed in part a.
 a. Develop a new unconstrained model that minimizes the sum of the demand-weighted distance defined as the product of the demand (measured in number of trips) and the distance to the warehouse.
a. Develop a new unconstrained model that minimizes the sum of the demand-weighted distance defined as the product of the demand (measured in number of trips) and the distance to the warehouse.b. Solve the model you developed in part a.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
54
The exponential smoothing model is given by,
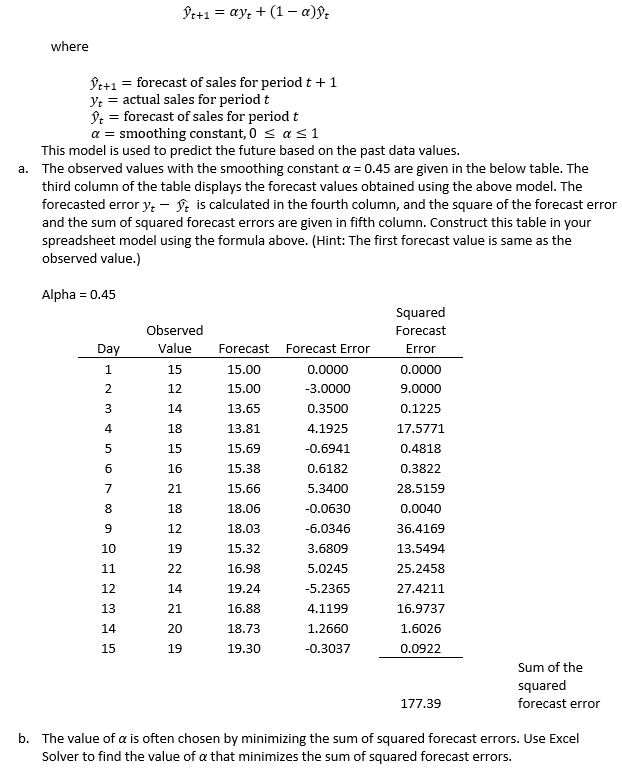


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
55
Mark and his friends are planning for a holiday party. Data on longitude, latitude, and number of friends at each of the 10 locations are given below. Mark would like to identify the location for the holiday party such that it minimizes the demand-weighted distance, where demand is the number of friends at each location. Find the optimal location for the party. The distance between two cities can be approximated by the following formula
where lat1 and long1 are the latitude and longitude of city 1, and lat2 and long2 are the latitude and longitude of city 2. (Hint: Notice that all longitude values given for this problem are negative. Make sure that you do not check the option for Make Unconstrained Variables Non-Negative in Solver.)

where lat1 and long1 are the latitude and longitude of city 1, and lat2 and long2 are the latitude and longitude of city 2. (Hint: Notice that all longitude values given for this problem are negative. Make sure that you do not check the option for Make Unconstrained Variables Non-Negative in Solver.)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
56
Consider the following data on the returns from bonds:

Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.

Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
57
Jeff is willing to invest $5000 in buying shares and bonds of a company to gain maximum returns. From his past experience, he estimates the relationship between returns and investments made in this company to be:
where,
R = total returns in thousands of dollars
S = thousands of dollars spent on Shares
B = thousands of dollars spent on Bond
Jeff would like to develop a strategy that will lead to maximum return subject to the restriction provided on amount available for investment. a. What is the value of return if $3,000 is invested in shares and $2,000 is invested bonds of the company?
b. Formulate an optimization problem that can be solved to maximize the returns subject to investing no more than $5,000 on both share and bonds.
c. Determine the optimal amount to invest in shares and bonds of the company. How much return will Jeff gain? Round all your answers to two decimal places.
where,
R = total returns in thousands of dollars
S = thousands of dollars spent on Shares
B = thousands of dollars spent on Bond
Jeff would like to develop a strategy that will lead to maximum return subject to the restriction provided on amount available for investment. a. What is the value of return if $3,000 is invested in shares and $2,000 is invested bonds of the company?
b. Formulate an optimization problem that can be solved to maximize the returns subject to investing no more than $5,000 on both share and bonds.
c. Determine the optimal amount to invest in shares and bonds of the company. How much return will Jeff gain? Round all your answers to two decimal places.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
58
An Electrical Company has two manufacturing plants. The cost in dollars of producing an Amplifier at each of the two plants is given below. The cost of producing Q1 Amplifiers at first plant is:
65Q₁ + 4Q₁²+ 90
and the cost of producing Q₂ Amplifiers at the second plant is
20Q₂ + 2Q₂²+ 120
The company needs to manufacture at least 60 Amplifiers to meet the received orders. How many Amplifiers should be produced at each of the plant to minimize the total production cost? Round the answers to two decimal places and the total cost to the nearest dollar value.
65Q₁ + 4Q₁²+ 90
and the cost of producing Q₂ Amplifiers at the second plant is
20Q₂ + 2Q₂²+ 120
The company needs to manufacture at least 60 Amplifiers to meet the received orders. How many Amplifiers should be produced at each of the plant to minimize the total production cost? Round the answers to two decimal places and the total cost to the nearest dollar value.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
59
Jim is trying to solve a problem where point A should be within the radius of 15cms from the points B, C, D, E and F. The decision variables are defined as below.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below:
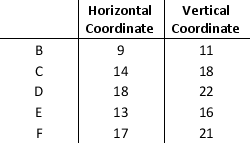
Formulate a model to find the optimal location of the point A.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below:

Formulate a model to find the optimal location of the point A.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck
60
Consider the EOQ model for multiple products that are independent except for a budget restriction. The following model describes this situation:
Let Dk = annual demand for product k
Ck = unit cost of product k
Sk = cost per order placed for product k
i = inventory carrying charge as a percentage of the cost per unit
B = the maximum amount of investment in goods
N = number of products
The decision variables are Qk, the amount of product k to order. The model is:
s.t. a. Set up a spreadsheet model and for the following data:
 b. Solve the problem using Excel Solver. (Hint: For Solver to find a solution, you need to start with decision variable values that are greater than 0.)
b. Solve the problem using Excel Solver. (Hint: For Solver to find a solution, you need to start with decision variable values that are greater than 0.)
Let Dk = annual demand for product k
Ck = unit cost of product k
Sk = cost per order placed for product k
i = inventory carrying charge as a percentage of the cost per unit
B = the maximum amount of investment in goods
N = number of products
The decision variables are Qk, the amount of product k to order. The model is:
s.t. a. Set up a spreadsheet model and for the following data:
 b. Solve the problem using Excel Solver. (Hint: For Solver to find a solution, you need to start with decision variable values that are greater than 0.)
b. Solve the problem using Excel Solver. (Hint: For Solver to find a solution, you need to start with decision variable values that are greater than 0.)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 60 في هذه المجموعة.
فتح الحزمة
k this deck








