تكلم مع الذكاء الاصطناعي
Deck 19: A: Cost Minimization
ملء الشاشة (f)
سؤال
سؤال
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 
must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 84 units of output is
A) $598.
B) $420.
C) $462.
D) $504.
E) $299.
must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 84 units of output isA) $598.
B) $420.
C) $462.
D) $504.
E) $299.
سؤال
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 
must use 9 machines. If the cost of labor is $7 per unit and the cost of machines is $9 per unit, the short-run total cost of producing 96 units of output is
A) $1,058.
B) $672.
C) $864.
D) $768.
E) $529.
must use 9 machines. If the cost of labor is $7 per unit and the cost of machines is $9 per unit, the short-run total cost of producing 96 units of output isA) $1,058.
B) $672.
C) $864.
D) $768.
E) $529.
سؤال
سؤال
سؤال
In Problem 3, the production function is f(L, M) 
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $36 per unit, then the total cost of producing 4 units of output will be
A) $84.
B) $170.
C) $144.
D) $168.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $36 per unit, then the total cost of producing 4 units of output will beA) $84.
B) $170.
C) $144.
D) $168.
E) None of the above.
سؤال
سؤال
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 
must use 9 machines. If the cost of labor is $10 per unit and the cost of machines is $4 per unit, the short-run total cost of producing 60 units of output is
A) $420.
B) $600.
C) $240.
D) $572.
E) $286.
must use 9 machines. If the cost of labor is $10 per unit and the cost of machines is $4 per unit, the short-run total cost of producing 60 units of output isA) $420.
B) $600.
C) $240.
D) $572.
E) $286.
سؤال
سؤال
سؤال
In Problem 3, the production function is f(L, M) = 
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $25 per unit, then the total cost of producing 7 units of output will be
A) $122.50.
B) $259.
C) $175.
D) $245.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $25 per unit, then the total cost of producing 7 units of output will beA) $122.50.
B) $259.
C) $175.
D) $245.
E) None of the above.
سؤال
سؤال
سؤال
In Problem 3, the production function is f(L, M) 
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $25 per unit and the cost of machines is $64 per unit, then the total cost of producing 6 units of output will be
A) $240.
B) $150.
C) $267.
D) $120.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $25 per unit and the cost of machines is $64 per unit, then the total cost of producing 6 units of output will beA) $240.
B) $150.
C) $267.
D) $120.
E) None of the above.
سؤال
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 
must use 4 machines. If the cost of labor is $10 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 64 units of output is
A) $512.
B) $384.
C) $640.
D) $1,328.
E) $664.
must use 4 machines. If the cost of labor is $10 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 64 units of output isA) $512.
B) $384.
C) $640.
D) $1,328.
E) $664.
سؤال
سؤال
In Problem 3, the production function is f(L, M) 
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $9 per unit and the cost of machines is $81 per unit, then the total cost of producing 10 units of output will be
A) $270.
B) $90.
C) $135.
D) $450.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $9 per unit and the cost of machines is $81 per unit, then the total cost of producing 10 units of output will beA) $270.
B) $90.
C) $135.
D) $450.
E) None of the above.
سؤال
In Problem 3, the production function is f(L, M) 
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $100 per unit and the cost of machines is $16 per unit, then the total cost of producing 7 units of output will be
A) $140.
B) $406.
C) $112.
D) $280.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $100 per unit and the cost of machines is $16 per unit, then the total cost of producing 7 units of output will beA) $140.
B) $406.
C) $112.
D) $280.
E) None of the above.
سؤال
سؤال
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 
must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $5 per unit, the short-run total cost of producing 108 units of output is
A) $900.
B) $540.
C) $540.
D) $540.
E) $450.
must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $5 per unit, the short-run total cost of producing 108 units of output isA) $900.
B) $540.
C) $540.
D) $540.
E) $450.
سؤال
In Problem 12, Al's production function for deer is f(x1, x2) 
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $4 per unit, then the cost of producing 8 deer is
A) $16.
B) $96.
C) $256.
D) $128.
E) $32.
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $4 per unit, then the cost of producing 8 deer isA) $16.
B) $96.
C) $256.
D) $128.
E) $32.
سؤال
In Problem 12, Al's production function for deer is f(x1, x2) 
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer is
A) $55.
B) $10.
C) $50.
D) $75.
E) $15.
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer isA) $55.
B) $10.
C) $50.
D) $75.
E) $15.
سؤال
In Problem 12, Al's production function for deer is f(x1, x2) 
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $1 per unit, then the cost of producing 7 deer is
A) $49.
B) $119.
C) $196.
D) $7.
E) $28.
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $1 per unit, then the cost of producing 7 deer isA) $49.
B) $119.
C) $196.
D) $7.
E) $28.
سؤال
Two firms, Wickedly Efficient Widgets (WEW) and Wildly Nepotistic Widgets (WNW), both produce widgets with the same production function 
, where K is the input of capital and L is the input of labor. Each company can hire labor at $1 per unit and capital at $1 per unit. WEW produces 10 widgets per week, choosing its input combination so as to produce these 10 widgets in the cheapest way possible. WNW also produces 10 widgets per week, but its dotty CEO requires it to use twice as much labor as WEW uses. Given that it must use twice as many laborers as WEW does and must produce the same output, how much larger are WNW's total costs than WEW's?
A) $10 per week
B) $20 per week
C) $15 per week
D) $5 per week
E) $2 per week
, where K is the input of capital and L is the input of labor. Each company can hire labor at $1 per unit and capital at $1 per unit. WEW produces 10 widgets per week, choosing its input combination so as to produce these 10 widgets in the cheapest way possible. WNW also produces 10 widgets per week, but its dotty CEO requires it to use twice as much labor as WEW uses. Given that it must use twice as many laborers as WEW does and must produce the same output, how much larger are WNW's total costs than WEW's?A) $10 per week
B) $20 per week
C) $15 per week
D) $5 per week
E) $2 per week
سؤال
In Problem 12, Al's production function for deer is f(x1, x2) 
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $1 per unit, then the cost of producing 4 deer is
A) $32.
B) $16.
C) $36.
D) $4.
E) $8.
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $1 per unit, then the cost of producing 4 deer isA) $32.
B) $16.
C) $36.
D) $4.
E) $8.
سؤال
In Problem 12, Al's production function for deer is f(x1, x2) 
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer is
A) $15.
B) $100.
C) $95.
D) $75.
E) $20.
, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer isA) $15.
B) $100.
C) $95.
D) $75.
E) $20.
فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/26
العب
ملء الشاشة (f)
Deck 19: A: Cost Minimization
1
In Problem 2, suppose that a new alloy is invented which uses copper and zinc in fixed proportions where 1 unit of output requires 5 units of copper and 3 units of zinc for each unit of alloy produced. If no other inputs are needed, the price of copper is $4, and the price of zinc is $2, what is the average cost per unit when 3,000 units of the alloy are produced?
A) $26
B) $13.33
C) $666.67
D) $.67
E) $13,333.33
A) $26
B) $13.33
C) $666.67
D) $.67
E) $13,333.33
A
2
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 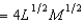must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 84 units of output is
A) $598.
B) $420.
C) $462.
D) $504.
E) $299.
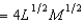must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 84 units of output isA) $598.
B) $420.
C) $462.
D) $504.
E) $299.
E
3
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) must use 9 machines. If the cost of labor is $7 per unit and the cost of machines is $9 per unit, the short-run total cost of producing 96 units of output is
A) $1,058.
B) $672.
C) $864.
D) $768.
E) $529.
must use 9 machines. If the cost of labor is $7 per unit and the cost of machines is $9 per unit, the short-run total cost of producing 96 units of output isA) $1,058.
B) $672.
C) $864.
D) $768.
E) $529.
E
4
Suppose that Nadine in Problem 1 has a production function 4x1 + x2. If the factor prices are $12 for factor 1 and $2 for factor 2, how much will it cost her to produce 50 units of output?
A) $100
B) $2,500
C) $150
D) $1,325
E) $125
A) $100
B) $2,500
C) $150
D) $1,325
E) $125
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
5
Suppose that Nadine in Problem 1 has a production function 4x1 + x2. If the factor prices are $4 for factor 1 and $2 for factor 2, how much will it cost her to produce 70 units of output?
A) $700
B) $1,260
C) $140
D) $70
E) $105
A) $700
B) $1,260
C) $140
D) $70
E) $105
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
6
In Problem 3, the production function is f(L, M) 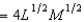, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $36 per unit, then the total cost of producing 4 units of output will be
A) $84.
B) $170.
C) $144.
D) $168.
E) None of the above.
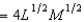, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $36 per unit, then the total cost of producing 4 units of output will beA) $84.
B) $170.
C) $144.
D) $168.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
7
In Problem 2, suppose that a new alloy is invented which uses copper and zinc in fixed proportions where 1 unit of output requires 3 units of copper and 4 units of zinc for each unit of alloy produced. If no other inputs are needed, the price of copper is $2, and the price of zinc is $3, what is the average cost per unit when 3,000 units of the alloy are produced?
A) $18
B) $.67
C) $666.67
D) $9.33
E) $9,333.33
A) $18
B) $.67
C) $666.67
D) $9.33
E) $9,333.33
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
8
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 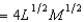must use 9 machines. If the cost of labor is $10 per unit and the cost of machines is $4 per unit, the short-run total cost of producing 60 units of output is
A) $420.
B) $600.
C) $240.
D) $572.
E) $286.
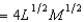must use 9 machines. If the cost of labor is $10 per unit and the cost of machines is $4 per unit, the short-run total cost of producing 60 units of output isA) $420.
B) $600.
C) $240.
D) $572.
E) $286.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
9
Suppose that Nadine in Problem 1 has a production function 5x1 + x2. If the factor prices are $10 for factor 1 and $3 for factor 2, how much will it cost her to produce 70 units of output?
A) $1,960
B) $3,710
C) $140
D) $210
E) $175
A) $1,960
B) $3,710
C) $140
D) $210
E) $175
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
10
Suppose that Nadine in Problem 1 has a production function 3x1 + x2. If the factor prices are $3 for factor 1 and $3 for factor 2, how much will it cost her to produce 80 units of output?
A) $960
B) $80
C) $240
D) $600
E) $160
A) $960
B) $80
C) $240
D) $600
E) $160
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
11
In Problem 3, the production function is f(L, M) = , where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $25 per unit, then the total cost of producing 7 units of output will be
A) $122.50.
B) $259.
C) $175.
D) $245.
E) None of the above.
, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $49 per unit and the cost of machines is $25 per unit, then the total cost of producing 7 units of output will beA) $122.50.
B) $259.
C) $175.
D) $245.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
12
In Problem 2, suppose that a new alloy is invented which uses copper and zinc in fixed proportions where 1 unit of output requires 4 units of copper and 4 units of zinc for each unit of alloy produced. If no other inputs are needed, the price of copper is $5, and the price of zinc is $2, what is the average cost per unit when 2,000 units of the alloy are produced?
A) $14.25
B) $.50
C) $28
D) $500
E) $14,250
A) $14.25
B) $.50
C) $28
D) $500
E) $14,250
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
13
Suppose that Nadine in Problem 1 has a production function 3x1 + x2. If the factor prices are $12 for factor 1 and $3 for factor 2, how much will it cost her to produce 20 units of output?
A) $430
B) $780
C) $60
D) $80
E) $70
A) $430
B) $780
C) $60
D) $80
E) $70
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
14
In Problem 3, the production function is f(L, M) 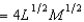, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $25 per unit and the cost of machines is $64 per unit, then the total cost of producing 6 units of output will be
A) $240.
B) $150.
C) $267.
D) $120.
E) None of the above.
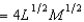, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $25 per unit and the cost of machines is $64 per unit, then the total cost of producing 6 units of output will beA) $240.
B) $150.
C) $267.
D) $120.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
15
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) must use 4 machines. If the cost of labor is $10 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 64 units of output is
A) $512.
B) $384.
C) $640.
D) $1,328.
E) $664.
must use 4 machines. If the cost of labor is $10 per unit and the cost of machines is $6 per unit, the short-run total cost of producing 64 units of output isA) $512.
B) $384.
C) $640.
D) $1,328.
E) $664.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
16
In Problem 2, suppose that a new alloy is invented which uses copper and zinc in fixed proportions where 1 unit of output requires 3 units of copper and 3 units of zinc for each unit of alloy produced. If no other inputs are needed, the price of copper is $4, and the price of zinc is $5, what is the average cost per unit when 4,000 units of the alloy are produced?
A) $1.33
B) $14.17
C) $1,333.33
D) $27
E) $14,166.67
A) $1.33
B) $14.17
C) $1,333.33
D) $27
E) $14,166.67
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
17
In Problem 3, the production function is f(L, M) 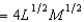, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $9 per unit and the cost of machines is $81 per unit, then the total cost of producing 10 units of output will be
A) $270.
B) $90.
C) $135.
D) $450.
E) None of the above.
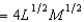, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $9 per unit and the cost of machines is $81 per unit, then the total cost of producing 10 units of output will beA) $270.
B) $90.
C) $135.
D) $450.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
18
In Problem 3, the production function is f(L, M) 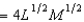, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $100 per unit and the cost of machines is $16 per unit, then the total cost of producing 7 units of output will be
A) $140.
B) $406.
C) $112.
D) $280.
E) None of the above.
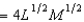, where L is the number of units of labor and M is the number of machines used. If the cost of labor is $100 per unit and the cost of machines is $16 per unit, then the total cost of producing 7 units of output will beA) $140.
B) $406.
C) $112.
D) $280.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
19
In Problem 2, suppose that a new alloy is invented which uses copper and zinc in fixed proportions where 1 unit of output requires 3 units of copper and 3 units of zinc for each unit of alloy produced. If no other inputs are needed, the price of copper is $3, and the price of zinc is $3, what is the average cost per unit when 4,000 units of the alloy are produced?
A) $9.50
B) $1,000
C) $1
D) $18
E) $9,500
A) $9.50
B) $1,000
C) $1
D) $18
E) $9,500
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
20
Suppose that in the short run, the firm in Problem 3 which has production function F(L, M) 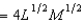must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $5 per unit, the short-run total cost of producing 108 units of output is
A) $900.
B) $540.
C) $540.
D) $540.
E) $450.
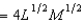must use 9 machines. If the cost of labor is $5 per unit and the cost of machines is $5 per unit, the short-run total cost of producing 108 units of output isA) $900.
B) $540.
C) $540.
D) $540.
E) $450.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
21
In Problem 12, Al's production function for deer is f(x1, x2) 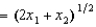, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $4 per unit, then the cost of producing 8 deer is
A) $16.
B) $96.
C) $256.
D) $128.
E) $32.
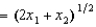, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $4 per unit, then the cost of producing 8 deer isA) $16.
B) $96.
C) $256.
D) $128.
E) $32.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
22
In Problem 12, Al's production function for deer is f(x1, x2) 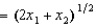, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer is
A) $55.
B) $10.
C) $50.
D) $75.
E) $15.
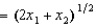, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer isA) $55.
B) $10.
C) $50.
D) $75.
E) $15.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
23
In Problem 12, Al's production function for deer is f(x1, x2) 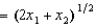, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $1 per unit, then the cost of producing 7 deer is
A) $49.
B) $119.
C) $196.
D) $7.
E) $28.
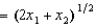, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $1 per unit, then the cost of producing 7 deer isA) $49.
B) $119.
C) $196.
D) $7.
E) $28.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
24
Two firms, Wickedly Efficient Widgets (WEW) and Wildly Nepotistic Widgets (WNW), both produce widgets with the same production function , where K is the input of capital and L is the input of labor. Each company can hire labor at $1 per unit and capital at $1 per unit. WEW produces 10 widgets per week, choosing its input combination so as to produce these 10 widgets in the cheapest way possible. WNW also produces 10 widgets per week, but its dotty CEO requires it to use twice as much labor as WEW uses. Given that it must use twice as many laborers as WEW does and must produce the same output, how much larger are WNW's total costs than WEW's?
A) $10 per week
B) $20 per week
C) $15 per week
D) $5 per week
E) $2 per week
, where K is the input of capital and L is the input of labor. Each company can hire labor at $1 per unit and capital at $1 per unit. WEW produces 10 widgets per week, choosing its input combination so as to produce these 10 widgets in the cheapest way possible. WNW also produces 10 widgets per week, but its dotty CEO requires it to use twice as much labor as WEW uses. Given that it must use twice as many laborers as WEW does and must produce the same output, how much larger are WNW's total costs than WEW's?A) $10 per week
B) $20 per week
C) $15 per week
D) $5 per week
E) $2 per week
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
25
In Problem 12, Al's production function for deer is f(x1, x2) 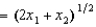, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $1 per unit, then the cost of producing 4 deer is
A) $32.
B) $16.
C) $36.
D) $4.
E) $8.
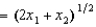, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $4 per unit and the cost of wood is $1 per unit, then the cost of producing 4 deer isA) $32.
B) $16.
C) $36.
D) $4.
E) $8.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
26
In Problem 12, Al's production function for deer is f(x1, x2) 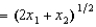, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer is
A) $15.
B) $100.
C) $95.
D) $75.
E) $20.
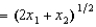, where x1 is the amount of plastic and x2 is the amount of wood used. If the cost of plastic is $8 per unit and the cost of wood is $3 per unit, then the cost of producing 5 deer isA) $15.
B) $100.
C) $95.
D) $75.
E) $20.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
فتح الحزمة
k this deck
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 26 في هذه المجموعة.
