تكلم مع الذكاء الاصطناعي
Deck 33: A: Externalities
ملء الشاشة (f)
سؤال
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 
- 1A and the cost function of the apple orchard is CA(H, A) = 
, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = A2 = 200.
B) A1 = 100 and A2 = 200.
C) A1 = 125 and A2 = 200.
D) A1 = 200 and A2 = 250.
E) A1 = 100 and A2 = 200.
- 1A and the cost function of the apple orchard is CA(H, A) = , where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = A2 = 200.
B) A1 = 100 and A2 = 200.
C) A1 = 125 and A2 = 200.
D) A1 = 200 and A2 = 250.
E) A1 = 100 and A2 = 200.
سؤال
سؤال
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 
- 3A and the cost function of the apple orchard is CA(H, A) = 
, where H and A are the number of units of honey and apples produced respectively. The price of honey is $7 and the price of apples is $5 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 125 and A2 = 250.
B) A1 = A2 = 250.
C) A1 = 200 and A2 = 250.
D) A1 = 250 and A2 = 400.
E) A1 = 350 and A2 = 250.
- 3A and the cost function of the apple orchard is CA(H, A) = , where H and A are the number of units of honey and apples produced respectively. The price of honey is $7 and the price of apples is $5 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 125 and A2 = 250.
B) A1 = A2 = 250.
C) A1 = 200 and A2 = 250.
D) A1 = 250 and A2 = 400.
E) A1 = 350 and A2 = 250.
سؤال
سؤال
سؤال
سؤال
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 
- 1A and the cost function of the apple orchard is CA(H, A) = 
, where H and A are the number of units of honey and apples produced respectively. The price of honey is $8 and the price of apples is $6 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 175 and A2 = 300.
B) A1 = 150 and A2 = 300.
C) A1 = 300 and A2 = 350.
D) A1 = A2 = 300.
E) A1 = 400 and A2 = 300.
- 1A and the cost function of the apple orchard is CA(H, A) = , where H and A are the number of units of honey and apples produced respectively. The price of honey is $8 and the price of apples is $6 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 175 and A2 = 300.
B) A1 = 150 and A2 = 300.
C) A1 = 300 and A2 = 350.
D) A1 = A2 = 300.
E) A1 = 400 and A2 = 300.
سؤال
سؤال
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 
- 2A and the cost function of the apple orchard is CA(H, A) = 
, where H and A are the number of units of honey and apples produced respectively. The price of honey is $5 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 200 and A2 = 300.
B) A1 = A2 = 200.
C) A1 = 100 and A2 = 200.
D) A1 = 150 and A2 = 200.
E) A1 = 250 and A2 = 200.
- 2A and the cost function of the apple orchard is CA(H, A) = , where H and A are the number of units of honey and apples produced respectively. The price of honey is $5 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 200 and A2 = 300.
B) A1 = A2 = 200.
C) A1 = 100 and A2 = 200.
D) A1 = 150 and A2 = 200.
E) A1 = 250 and A2 = 200.
سؤال
سؤال
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 
- 3A and the cost function of the apple orchard is CA(H, A) = 
, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $7 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 250 and A2 = 350.
B) A1 = A2 = 350.
C) A1 = 175 and A2 = 350.
D) A1 = 350 and A2 = 500.
E) A1 = 100 and A2 = 350.
- 3A and the cost function of the apple orchard is CA(H, A) = , where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $7 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 250 and A2 = 350.
B) A1 = A2 = 350.
C) A1 = 175 and A2 = 350.
D) A1 = 350 and A2 = 500.
E) A1 = 100 and A2 = 350.
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/25
العب
ملء الشاشة (f)
Deck 33: A: Externalities
1
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 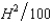- 1A and the cost function of the apple orchard is CA(H, A) = 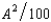, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = A2 = 200.
B) A1 = 100 and A2 = 200.
C) A1 = 125 and A2 = 200.
D) A1 = 200 and A2 = 250.
E) A1 = 100 and A2 = 200.
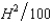- 1A and the cost function of the apple orchard is CA(H, A) = 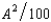, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = A2 = 200.
B) A1 = 100 and A2 = 200.
C) A1 = 125 and A2 = 200.
D) A1 = 200 and A2 = 250.
E) A1 = 100 and A2 = 200.
D
2
In Problem 3, suppose Wilfred, a typical citizen, has the utility function U(m, d, h) = m + 13d2 - d2 - 4h, where d is the number of hours per day that he spends driving around, h is the average number of hours per day spent driving around by other people in his home town, and m is the amount of money he has left to spend on other stuff besides gasoline and auto repairs. Gas and auto repairs cost $1 per hour of driving. If each citizen believes that their own driving will not affect the amount of driving done by others, they will all drive D1 hours per day. If all citizens drive to maximize the utility of a typical citizen, they will all drive D2 hours per day, where
A) D1 = 6 and D2 = 4.
B) D1 = D2 = 6.
C) D1 = 8 and D2 = 5.
D) D1 = 9 and D2 = 0.
E) D1 = 6 and D2 = 2.
A) D1 = 6 and D2 = 4.
B) D1 = D2 = 6.
C) D1 = 8 and D2 = 5.
D) D1 = 9 and D2 = 0.
E) D1 = 6 and D2 = 2.
A
3
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 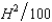- 3A and the cost function of the apple orchard is CA(H, A) = 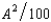, where H and A are the number of units of honey and apples produced respectively. The price of honey is $7 and the price of apples is $5 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 125 and A2 = 250.
B) A1 = A2 = 250.
C) A1 = 200 and A2 = 250.
D) A1 = 250 and A2 = 400.
E) A1 = 350 and A2 = 250.
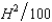- 3A and the cost function of the apple orchard is CA(H, A) = 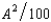, where H and A are the number of units of honey and apples produced respectively. The price of honey is $7 and the price of apples is $5 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 125 and A2 = 250.
B) A1 = A2 = 250.
C) A1 = 200 and A2 = 250.
D) A1 = 250 and A2 = 400.
E) A1 = 350 and A2 = 250.
D
4
In Problem 3, suppose Harry, a typical citizen, has the utility function U(m, d, h) = m + 7d2 - d2 - 2h, where d is the number of hours per day that he spends driving around, h is the average number of hours per day spent driving around by other people in his home town, and m is the amount of money he has left to spend on other stuff besides gasoline and auto repairs. Gas and auto repairs cost $1 per hour of driving. If each citizen believes that their own driving will not affect the amount of driving done by others, they will all drive D1 hours per day. If all citizens drive to maximize the utility of a typical citizen, they will all drive D2 hours per day, where
A) D1 = 6 and D2 = 1.
B) D1 = 5 and D2 = 3.
C) D1 = D2 = 3.
D) D1 = 3 and D2 = 2.
E) D1 = 3 and D2 = 0.
A) D1 = 6 and D2 = 1.
B) D1 = 5 and D2 = 3.
C) D1 = D2 = 3.
D) D1 = 3 and D2 = 2.
E) D1 = 3 and D2 = 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
5
An airport is located next to a housing development. Where X is the number of planes that land per day and Y is the number of houses in the housing development, profits of the airport are 22X - X2 and profits of the developer are 26Y - Y2 - XY. Let H1 be the number of houses built if a single profit-maximizing company owns the airport and the housing development. Let H2 be the number of houses built if the airport and the housing development are operated independently and the airport has to pay the developer the total "damages" XY done by the planes to the developer's profits.
A) H1 = H2 = 10.
B) H1 = 10 and H2 = 13.
C) H1 = 13 and H2 = 10.
D) H1 = 12 and H2 = 12.
E) H1 = 12 and H2 = 16.
A) H1 = H2 = 10.
B) H1 = 10 and H2 = 13.
C) H1 = 13 and H2 = 10.
D) H1 = 12 and H2 = 12.
E) H1 = 12 and H2 = 16.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
6
An airport is located next to a housing development. Where X is the number of planes that land per day and Y is the number of houses in the housing development, profits of the airport are 38X - X2 and profits of the developer are 28Y - Y2 - XY. Let H1 be the number of houses built if a single profit-maximizing company owns the airport and the housing development. Let H2 be the number of houses built if the airport and the housing development are operated independently and the airport has to pay the developer the total "damages" XY done by the planes to the developer's profits.
A) H1 = H2 = 6.
B) H1 = 14 and H2 = 6.
C) H1 = 6 and H2 = 14.
D) H1 = 8 and H2 = 13.
E) H1 = 13 and H2 = 17.
A) H1 = H2 = 6.
B) H1 = 14 and H2 = 6.
C) H1 = 6 and H2 = 14.
D) H1 = 8 and H2 = 13.
E) H1 = 13 and H2 = 17.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
7
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 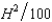- 1A and the cost function of the apple orchard is CA(H, A) = 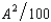, where H and A are the number of units of honey and apples produced respectively. The price of honey is $8 and the price of apples is $6 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 175 and A2 = 300.
B) A1 = 150 and A2 = 300.
C) A1 = 300 and A2 = 350.
D) A1 = A2 = 300.
E) A1 = 400 and A2 = 300.
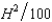- 1A and the cost function of the apple orchard is CA(H, A) = 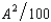, where H and A are the number of units of honey and apples produced respectively. The price of honey is $8 and the price of apples is $6 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 175 and A2 = 300.
B) A1 = 150 and A2 = 300.
C) A1 = 300 and A2 = 350.
D) A1 = A2 = 300.
E) A1 = 400 and A2 = 300.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
8
An airport is located next to a housing development. Where X is the number of planes that land per day and Y is the number of houses in the housing development, profits of the airport are 22X - X2 and profits of the developer are 32Y - Y2 - XY. Let H1 be the number of houses built if a single profit-maximizing company owns the airport and the housing development. Let H2 be the number of houses built if the airport and the housing development are operated independently and the airport has to pay the developer the total "damages" XY done by the planes to the developer's profits.
A) H1 = 16 and H2 = 15.
B) H1 = 14 and H2 = 16.
C) H1 = 16 and H2 = 14.
D) H1 = H2 = 14.
E) H1 = 15 and H2 = 19.
A) H1 = 16 and H2 = 15.
B) H1 = 14 and H2 = 16.
C) H1 = 16 and H2 = 14.
D) H1 = H2 = 14.
E) H1 = 15 and H2 = 19.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
9
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 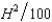- 2A and the cost function of the apple orchard is CA(H, A) = 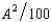, where H and A are the number of units of honey and apples produced respectively. The price of honey is $5 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 200 and A2 = 300.
B) A1 = A2 = 200.
C) A1 = 100 and A2 = 200.
D) A1 = 150 and A2 = 200.
E) A1 = 250 and A2 = 200.
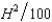- 2A and the cost function of the apple orchard is CA(H, A) = 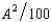, where H and A are the number of units of honey and apples produced respectively. The price of honey is $5 and the price of apples is $4 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 200 and A2 = 300.
B) A1 = A2 = 200.
C) A1 = 100 and A2 = 200.
D) A1 = 150 and A2 = 200.
E) A1 = 250 and A2 = 200.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
10
In Problem 3, suppose Lawrence, a typical citizen, has the utility function U(m, d, h) = m + 7d2 - d2 - 4h, where d is the number of hours per day that he spends driving around, h is the average number of hours per day spent driving around by other people in his home town, and m is the amount of money he has left to spend on other stuff besides gasoline and auto repairs. Gas and auto repairs cost $1 per hour of driving. If each citizen believes that their own driving will not affect the amount of driving done by others, they will all drive D1 hours per day. If all citizens drive to maximize the utility of a typical citizen, they will all drive D2 hours per day, where
A) D1 = 5 and D2 = 2.
B) D1 = D2 = 3.
C) D1 = 3 and D2 = 1.
D) D1 = 6 and D2 = 0.
E) D1 = 3 and D2 = 0.
A) D1 = 5 and D2 = 2.
B) D1 = D2 = 3.
C) D1 = 3 and D2 = 1.
D) D1 = 6 and D2 = 0.
E) D1 = 3 and D2 = 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
11
In Problem 2, suppose that the cost function of the honey farm is CH(H, A) = 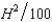- 3A and the cost function of the apple orchard is CA(H, A) = 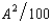, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $7 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.
A) A1 = 250 and A2 = 350.
B) A1 = A2 = 350.
C) A1 = 175 and A2 = 350.
D) A1 = 350 and A2 = 500.
E) A1 = 100 and A2 = 350.
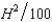- 3A and the cost function of the apple orchard is CA(H, A) = 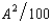, where H and A are the number of units of honey and apples produced respectively. The price of honey is $2 and the price of apples is $7 per unit. Let A1 be the output of apples if the firms operate independently, and let A2 be the output of apples if the firms are operated by a profit-maximizing single owner.A) A1 = 250 and A2 = 350.
B) A1 = A2 = 350.
C) A1 = 175 and A2 = 350.
D) A1 = 350 and A2 = 500.
E) A1 = 100 and A2 = 350.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
12
Suppose that in Horsehead, Massachusetts, the cost of operating a lobster boat is $6,000 per month. Suppose that if x lobster boats operate in the bay, the total monthly revenue from lobster boats in the bay is $1,000(18x - x2). If there are no restrictions on entry and new boats come into the bay until there is no profit to be made by a new entrant, then the number of boats who enter will be X1. If the number of boats that operate in the bay is regulated to maximize total profits, the number of boats in the bay will be X2.
A) X1 = 6 and X2 = 4.
B) X1 = 12 and X2 = 12.
C) X1 = 12 and X2 = 6.
D) X1 = 16 and X2 = 10.
E) None of the above.
A) X1 = 6 and X2 = 4.
B) X1 = 12 and X2 = 12.
C) X1 = 12 and X2 = 6.
D) X1 = 16 and X2 = 10.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
13
An airport is located next to a housing development. Where X is the number of planes that land per day and Y is the number of houses in the housing development, profits of the airport are 20X - X2 and profits of the developer are 28Y - Y2 - XY. Let H1 be the number of houses built if a single profit-maximizing company owns the airport and the housing development. Let H2 be the number of houses built if the airport and the housing development are operated independently and the airport has to pay the developer the total "damages" XY done by the planes to the developer's profits.
A) H1 = 12 and H2 = 14.
B) H1 = H2 = 12.
C) H1 = 14 and H2 = 13.
D) H1 = 14 and H2 = 12.
E) H1 = 13 and H2 = 17.
A) H1 = 12 and H2 = 14.
B) H1 = H2 = 12.
C) H1 = 14 and H2 = 13.
D) H1 = 14 and H2 = 12.
E) H1 = 13 and H2 = 17.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
14
Suppose that in Horsehead, Massachusetts, the cost of operating a lobster boat is $6,000 per month. Suppose that if x lobster boats operate in the bay, the total monthly revenue from lobster boats in the bay is $1,000(18x - x2). If there are no restrictions on entry and new boats come into the bay until there is no profit to be made by a new entrant, then the number of boats who enter will be X1. If the number of boats that operate in the bay is regulated to maximize total profits, the number of boats in the bay will be X2.
A) X1 = 6 and X2 = 4.
B) X1 = 12 and X2 = 6.
C) X1 = 16 and X2 = 10.
D) X1 = 12 and X2 = 12.
E) None of the above.
A) X1 = 6 and X2 = 4.
B) X1 = 12 and X2 = 6.
C) X1 = 16 and X2 = 10.
D) X1 = 12 and X2 = 12.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
15
In Problem 3, suppose Albert, a typical citizen, has the utility function U(m, d, h) = m + 5d2 - d2 - 2h, where d is the number of hours per day that he spends driving around, h is the average number of hours per day spent driving around by other people in his home town, and m is the amount of money he has left to spend on other stuff besides gasoline and auto repairs. Gas and auto repairs cost $1 per hour of driving. If each citizen believes that their own driving will not affect the amount of driving done by others, they will all drive D1 hours per day. If all citizens drive to maximize the utility of a typical citizen, they will all drive D2 hours per day, where
A) D1 = 5 and D2 = 0.
B) D1 = D2 = 2.
C) D1 = 2 and D2 = 1.
D) D1 = 4 and D2 = 2.
E) D1 = 2 and D2 = 0.
A) D1 = 5 and D2 = 0.
B) D1 = D2 = 2.
C) D1 = 2 and D2 = 1.
D) D1 = 4 and D2 = 2.
E) D1 = 2 and D2 = 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
16
Suppose that in Horsehead, Massachusetts, the cost of operating a lobster boat is $5,000 per month. Suppose that if x lobster boats operate in the bay, the total monthly revenue from lobster boats in the bay is $1,000(21x - x2). If there are no restrictions on entry and new boats come into the bay until there is no profit to be made by a new entrant, then the number of boats who enter will be X1. If the number of boats that operate in the bay is regulated to maximize total profits, the number of boats in the bay will be X2.
A) X1 = 16 and X2 = 16.
B) X1 = 20 and X2 = 12.
C) X1 = 16 and X2 = 8.
D) X1 = 8 and X2 = 6.
E) None of the above.
A) X1 = 16 and X2 = 16.
B) X1 = 20 and X2 = 12.
C) X1 = 16 and X2 = 8.
D) X1 = 8 and X2 = 6.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
17
In Problem 3, suppose Sam, a typical citizen, has the utility function U(m, d, h) = m + 13d2 - d2 - 6h, where d is the number of hours per day that he spends driving around, h is the average number of hours per day spent driving around by other people in his home town, and m is the amount of money he has left to spend on other stuff besides gasoline and auto repairs. Gas and auto repairs cost $1 per hour of driving. If each citizen believes that their own driving will not affect the amount of driving done by others, they will all drive D1 hours per day. If all citizens drive to maximize the utility of a typical citizen, they will all drive D2 hours per day, where
A) D1 = 8 and D2 = 4.
B) D1 = 6 and D2 = 3.
C) D1 = D2 = 6.
D) D1 = 9 and D2 = 0.
E) D1 = 6 and D2 = 1.
A) D1 = 8 and D2 = 4.
B) D1 = 6 and D2 = 3.
C) D1 = D2 = 6.
D) D1 = 9 and D2 = 0.
E) D1 = 6 and D2 = 1.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
18
An airport is located next to a housing development. Where X is the number of planes that land per day and Y is the number of houses in the housing development, profits of the airport are 22X - X2 and profits of the developer are 20Y - Y2 - XY. Let H1 be the number of houses built if a single profit-maximizing company owns the airport and the housing development. Let H2 be the number of houses built if the airport and the housing development are operated independently and the airport has to pay the developer the total "damages" XY done by the planes to the developer's profits.
A) H1 = 10 and H2 = 6.
B) H1 = 8 and H2 = 9.
C) H1 = 6 and H2 = 10.
D) H1 = H2 = 6.
E) H1 = 9 and H2 = 13.
A) H1 = 10 and H2 = 6.
B) H1 = 8 and H2 = 9.
C) H1 = 6 and H2 = 10.
D) H1 = H2 = 6.
E) H1 = 9 and H2 = 13.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
19
Suppose that in Horsehead, Massachusetts, the cost of operating a lobster boat is $2,000 per month. Suppose that if x lobster boats operate in the bay, the total monthly revenue from lobster boats in the bay is $1,000(10x - x2). If there are no restrictions on entry and new boats come into the bay until there is no profit to be made by a new entrant, then the number of boats who enter will be X1. If the number of boats that operate in the bay is regulated to maximize total profits, the number of boats in the bay will be X2.
A) X1 = 8 and X2 = 8.
B) X1 = 4 and X2 = 2.
C) X1 = 8 and X2 = 4.
D) X1 = 12 and X2 = 8.
E) None of the above.
A) X1 = 8 and X2 = 8.
B) X1 = 4 and X2 = 2.
C) X1 = 8 and X2 = 4.
D) X1 = 12 and X2 = 8.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
20
Suppose that in Horsehead, Massachusetts, the cost of operating a lobster boat is $2,000 per month. Suppose that if x lobster boats operate in the bay, the total monthly revenue from lobster boats in the bay is $1,000(26x - x2). If there are no restrictions on entry and new boats come into the bay until there is no profit to be made by a new entrant, then the number of boats who enter will be X1. If the number of boats that operate in the bay is regulated to maximize total profits, the number of boats in the bay will be X2.
A) X1 = 24 and X2 = 12.
B) X1 = 24 and X2 = 24.
C) X1 = 12 and X2 = 10.
D) X1 = 28 and X2 = 16.
E) None of the above.
A) X1 = 24 and X2 = 12.
B) X1 = 24 and X2 = 24.
C) X1 = 12 and X2 = 10.
D) X1 = 28 and X2 = 16.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
21
A clothing store and a jeweler are located side by side in a shopping mall. If the clothing store spends C dollars on advertising and the jeweler spends J dollars on advertising, then the profits of the clothing store will be (18 + J)C - C2 and the profits of the jeweler will be (24 + C)J - 2J2. The clothing store gets to choose its amount of advertising first, knowing that the jeweler will find out how much the clothing store advertised before deciding how much to spend. The amount spent by the clothing store will be a. 48.
B) 16.
C) 8.
D) 32.
E) 24.
B) 16.
C) 8.
D) 32.
E) 24.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
22
A clothing store and a jeweler are located side by side in a shopping mall. If the clothing store spends C dollars on advertising and the jeweler spends J dollars on advertising, then the profits of the clothing store will be (18 + J)C - C2 and the profits of the jeweler will be (36 + C)J - 2J2. The clothing store gets to choose its amount of advertising first, knowing that the jeweler will find out how much the clothing store advertised before deciding how much to spend. The amount spent by the clothing store will be a. 54.
B) 9.
C) 36.
D) 18.
E) 27.
B) 9.
C) 36.
D) 18.
E) 27.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
23
A clothing store and a jeweler are located side by side in a shopping mall. If the clothing store spends C dollars on advertising and the jeweler spends J dollars on advertising, then the profits of the clothing store will be (6 + J)C - C2 and the profits of the jeweler will be (6 + C)J - 2J2. The clothing store gets to choose its amount of advertising first, knowing that the jeweler will find out how much the clothing store advertised before deciding how much to spend. The amount spent by the clothing store will be a. 5.
B) 10.
C) 15.
D) 2.50.
E) 7.50.
B) 10.
C) 15.
D) 2.50.
E) 7.50.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
24
A clothing store and a jeweler are located side by side in a shopping mall. If the clothing store spends C dollars on advertising and the jeweler spends J dollars on advertising, then the profits of the clothing store will be (24 + J)C - C2 and the profits of the jeweler will be (66 + C)J - 2J2. The clothing store gets to choose its amount of advertising first, knowing that the jeweler will find out how much the clothing store advertised before deciding how much to spend. The amount spent by the clothing store will be a. 54.
B) 81.
C) 13.50.
D) 27.
E) 40.50.
B) 81.
C) 13.50.
D) 27.
E) 40.50.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
25
A clothing store and a jeweler are located side by side in a shopping mall. If the clothing store spends C dollars on advertising and the jeweler spends J dollars on advertising, then the profits of the clothing store will be (42 + J)C - C2 and the profits of the jeweler will be (54 + C)J - 2J2. The clothing store gets to choose its amount of advertising first, knowing that the jeweler will find out how much the clothing store advertised before deciding how much to spend. The amount spent by the clothing store will be a. 74.
B) 111.
C) 18.50.
D) 37.
E) 55.50.
B) 111.
C) 18.50.
D) 37.
E) 55.50.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
فتح الحزمة
k this deck
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 25 في هذه المجموعة.
