تكلم مع الذكاء الاصطناعي
Deck 11: Uncertainty
ملء الشاشة (f)
سؤال
سؤال
Prufrock is risk averse. He is offered a gamble in which with probability 
he will lose $1,000 and with probability 
, he will win $500.
A) Since he is risk averse, he will certainly not take the gamble.
B) Since the expected value of the gamble is positive, he will certainly take the gamble.
C) If Prufrock's initial wealth is greater than $1,500, he will certainly take the gamble.
D) If Prufrock's initial wealth is smaller than $1,500, he will certainly not take the gamble.
E) Not enough information is given to determine for sure whether he will take the gamble.
he will lose $1,000 and with probability , he will win $500.A) Since he is risk averse, he will certainly not take the gamble.
B) Since the expected value of the gamble is positive, he will certainly take the gamble.
C) If Prufrock's initial wealth is greater than $1,500, he will certainly take the gamble.
D) If Prufrock's initial wealth is smaller than $1,500, he will certainly not take the gamble.
E) Not enough information is given to determine for sure whether he will take the gamble.
سؤال
سؤال
Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 
), where W is his wealth. Buck's total wealth is $12,000. With probability .2 the palace will be a failure and he'll lose $9,000, so that his wealth will be just $3,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $12,000 with certainty?
A) $75,000
B) $14,250
C) $36,000
D) $48,000
E) $15,000
), where W is his wealth. Buck's total wealth is $12,000. With probability .2 the palace will be a failure and he'll lose $9,000, so that his wealth will be just $3,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $12,000 with certainty?A) $75,000
B) $14,250
C) $36,000
D) $48,000
E) $15,000
سؤال
Joe's wealth is $100 and he is an expected utility maximizer with a von Neumann-Morgenstern utility function 
Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?
A) $10
B) $15
C) $19
D) $100
E) $50
Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?A) $10
B) $15
C) $19
D) $100
E) $50
سؤال
Timmy Qualm's uncle gave him a lottery ticket. With probability 
the ticket will be worth $100 and with probability 
it will be worthless. Let x be Timmy's wealth if the lottery ticket is a winner, and y his wealth if it is a loser. Timmy's preferences over alternative contingent commodity bundles are represented by the utility function U(x, y) = min{ 2x - y, 2y - x}. He has no risks other than the ticket.
A) Timmy would sell his lottery ticket for $25 but not for less.
B) Timmy hates risk so much that he'd be willing to throw away the lottery ticket rather than worry about whether he won.
C) Timmy satisfies the expected utility hypothesis.
D) Timmy is misnamed. He is a risk lover.
E) None of the above.
the ticket will be worth $100 and with probability it will be worthless. Let x be Timmy's wealth if the lottery ticket is a winner, and y his wealth if it is a loser. Timmy's preferences over alternative contingent commodity bundles are represented by the utility function U(x, y) = min{ 2x - y, 2y - x}. He has no risks other than the ticket.A) Timmy would sell his lottery ticket for $25 but not for less.
B) Timmy hates risk so much that he'd be willing to throw away the lottery ticket rather than worry about whether he won.
C) Timmy satisfies the expected utility hypothesis.
D) Timmy is misnamed. He is a risk lover.
E) None of the above.
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
Oskar's preferences over gambles in which the probability of events 1 and 2 are both 
can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income of
A) $12.5.
B) $9.
C) $16.
D) $17.
E) None of the above.
can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income ofA) $12.5.
B) $9.
C) $16.
D) $17.
E) None of the above.
سؤال
سؤال
سؤال
سؤال
Clancy has $1,200. He plans to bet on a boxing match between Sullivan and Flanagan. For $4, he can buy a coupon that pays $10 if Sullivan wins and nothing otherwise. For $6 he can buy a coupon that will pay $10 if Flanagan wins and nothing otherwise. Clancy doesn't agree with these odds. He thinks that the two fighters each have a probability of 
of winning. If he is an expected utility maximizer who tries to maximize the expected value of lnW, where lnW is the natural log of his wealth, it would be rational for him to buy
A) 50 Sullivan coupons and no Flanagan coupons.
B) 100 Sullivan coupons and no Flanagan coupons.
C) 50 Flanagan coupons and no Sullivan coupons.
D) 100 Flanagan coupons and no Sullivan coupons.
E) 100 of each kind of coupon.
of winning. If he is an expected utility maximizer who tries to maximize the expected value of lnW, where lnW is the natural log of his wealth, it would be rational for him to buyA) 50 Sullivan coupons and no Flanagan coupons.
B) 100 Sullivan coupons and no Flanagan coupons.
C) 50 Flanagan coupons and no Sullivan coupons.
D) 100 Flanagan coupons and no Sullivan coupons.
E) 100 of each kind of coupon.
سؤال
Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 
), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?
A) $28,500
B) $150,000
C) $96,000
D) $72,000
E) $30,000
), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?A) $28,500
B) $150,000
C) $96,000
D) $72,000
E) $30,000
سؤال
سؤال
سؤال
سؤال
سؤال
Clancy has $1,800. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $9 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $1 each. Clancy believes that the two fighters each have a probability of 
of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?
A) Don't gamble at all.
B) Buy 100 Sullivan tickets and 900 Flanagan tickets.
C) Buy exactly as many Flanagan tickets as Sullivan tickets.
D) Buy 50 Sullivan tickets and 450 Flanagan tickets.
E) Buy 50 Sullivan tickets and 900 Flanagan tickets.
of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?A) Don't gamble at all.
B) Buy 100 Sullivan tickets and 900 Flanagan tickets.
C) Buy exactly as many Flanagan tickets as Sullivan tickets.
D) Buy 50 Sullivan tickets and 450 Flanagan tickets.
E) Buy 50 Sullivan tickets and 900 Flanagan tickets.
سؤال
Linus Piecewise is an expected utility maximizer. There are two events, H and T, which each have probability 
. Linus's preferences over lotteries in which his wealth is h if event H happens and t if event T happens are representable by the utility function 
. The function u takes the following form. For any x, u(x) = x if x < 100 and u(x) = 100 + 
if x is greater than or equal to 100. Draw a graph showing the indifference curves for Linus that pass through
a. the point (50, 0)
b. the point (50, 100)
c. the point (100, 100)
d. the point (150, 100)
. Linus's preferences over lotteries in which his wealth is h if event H happens and t if event T happens are representable by the utility function . The function u takes the following form. For any x, u(x) = x if x < 100 and u(x) = 100 + if x is greater than or equal to 100. Draw a graph showing the indifference curves for Linus that pass through a. the point (50, 0)
b. the point (50, 100)
c. the point (100, 100)
d. the point (150, 100)
سؤال
Quincy's expected utility function is pc 
1 + (1 - p)c 
2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .60 and $12,100 with probability .40. Wilbur will choose the sure payment if
A) Z > 6,400 and the lottery if Z < 6,400.
B) Z > 12,100 and the lottery if Z < 12,100.
C) Z > 9,250 and the lottery if Z < 9,250.
D) Z > 5,000 and the lottery if Z < 5,000.
E) Z > 7,000 and the lottery if Z < 7,000.
1 + (1 - p)c 2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .60 and $12,100 with probability .40. Wilbur will choose the sure payment if
A) Z > 6,400 and the lottery if Z < 6,400.
B) Z > 12,100 and the lottery if Z < 12,100.
C) Z > 9,250 and the lottery if Z < 9,250.
D) Z > 5,000 and the lottery if Z < 5,000.
E) Z > 7,000 and the lottery if Z < 7,000.
سؤال
Willy's only source of wealth is his chocolate factory. He has the utility function pc 
f + (1 - p)c 
nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
. The value of Willy's factory is $500,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 
whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy
A) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
f + (1 - p)c nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
. The value of Willy's factory is $500,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buyA) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
سؤال
Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function 
If Billy is not injured this season, he will receive an income of $25 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is
A) 100,000.
B) 9,020.
C) between 24 million and 25 million.
D) 4,510.
E) 18,040.
If Billy is not injured this season, he will receive an income of $25 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility isA) 100,000.
B) 9,020.
C) between 24 million and 25 million.
D) 4,510.
E) 18,040.
سؤال
After graduating, Sallie Handshake's best job offer will either be with a Big-8 accounting firm for $160,000 a year or as a State Farm agent in Grand Rapids, Michigan, for $40,000 a year. She can increase the probability of the former outcome by studying more, but such studying has its costs. If S represents her amount of studying (where S = 0 is no study and S = 1 is all-out effort), her probability of getting the job with a Big-8 firm just equals S. Her utility depends on how hard she studies and her subsequent annual income Y. She tries to maximize the expected value of the von Neuman-Morgenstern utility function 
If she chooses S to maximize her expected utility, how much will she study?
A) S = 0.1.
B) S = 0.25.
C) S = 0.5.
D) S = 0.75.
E) S = 0.9.
If she chooses S to maximize her expected utility, how much will she study?A) S = 0.1.
B) S = 0.25.
C) S = 0.5.
D) S = 0.75.
E) S = 0.9.
سؤال
The certainty equivalent of a gamble is defined to be the amount of money which, if you were promised it with certainty, would be indifferent to the gamble.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W
(where W is wealth) and if the probability of events 1 and 2 are both
, write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens.
b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W
(where W is wealth) and if the probability of events 1 and 2 are both
, write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens. b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
سؤال
Oliver takes his wealth of $1,000 to a casino. He can bet as much as he likes on the toss of a coin but the "house" takes a cut. If Oliver bets $x on heads, then if heads comes up, he gets $.8x and, if tails comes up, he pays $x. Similarly if he bets $x on tails and if tails comes up, he wins $.8x and, if heads comes up, he pays $x. Draw a graph with dollars contingent on heads and dollars contingent on tails on the two axes. Show Oliver's budget constraint. Oliver is an expected utility maximizer with the utility function 
, where h is his wealth if heads comes up and t is his wealth if tails comes up. Draw the highest indifference curve that Oliver can reach with his budget. What bets if any does he make?
, where h is his wealth if heads comes up and t is his wealth if tails comes up. Draw the highest indifference curve that Oliver can reach with his budget. What bets if any does he make? سؤال
Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function 
If Billy is not injured this season, he will receive an income of $16 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is
A) 3,610.
B) between 15 million and 16 million.
C) 100,000.
D) 7,220.
E) 14,440.
If Billy is not injured this season, he will receive an income of $16 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility isA) 3,610.
B) between 15 million and 16 million.
C) 100,000.
D) 7,220.
E) 14,440.
سؤال
Willy's only source of wealth is his chocolate factory. He has the utility function pc 
f + (1 - p)c 
nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
. The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 
whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy
A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance his wealth will beof what it would be if there were no flood.
f + (1 - p)c nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
. The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buyA) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance his wealth will beof what it would be if there were no flood.
سؤال
Clancy has $5,000. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $5 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $5 each. Clancy believes that the two fighters each have a probability of 
of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?
A) Buy exactly as many Flanagan tickets as Sullivan tickets.
B) Buy 250 Sullivan tickets and 250 Flanagan tickets.
C) Don't gamble at all.
D) Buy 500 Sullivan tickets and 500 Flanagan tickets.
E) Buy 250 Sullivan tickets and 500 Flanagan tickets.
of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?A) Buy exactly as many Flanagan tickets as Sullivan tickets.
B) Buy 250 Sullivan tickets and 250 Flanagan tickets.
C) Don't gamble at all.
D) Buy 500 Sullivan tickets and 500 Flanagan tickets.
E) Buy 250 Sullivan tickets and 500 Flanagan tickets.
سؤال
Yoram's expected utility function is pc 
1 + (1 - p)c 
2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
A) Z > 3,249 and the lottery if Z < 3,249.
B) Z > 2,874.50 and the lottery if Z < 2,874.50.
C) Z > 3,600 and the lottery if Z < 3,600.
D) Z > 3,424.50 and the lottery if Z < 3,424.50.
E) Z > 3,270 and the lottery if Z < 3,270.
1 + (1 - p)c 2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
A) Z > 3,249 and the lottery if Z < 3,249.
B) Z > 2,874.50 and the lottery if Z < 2,874.50.
C) Z > 3,600 and the lottery if Z < 3,600.
D) Z > 3,424.50 and the lottery if Z < 3,424.50.
E) Z > 3,270 and the lottery if Z < 3,270.
سؤال
سؤال
Portia has waited a long time for her ship to come in, and she has concluded that it will arrive today with probability 
. If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?
A) $1
B) $2
C) $2.50
D) $4
E) None of the above.
. If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?A) $1
B) $2
C) $2.50
D) $4
E) None of the above.
سؤال
Gaston Gourmand loves good food. Due to an unusual ailment, he has a probability of 
of losing his sense of smell, which would greatly reduce his enjoyment of food. Gaston finds an insurance company that will sell him insurance where Gaston gets $3x if he loses his smell and pays $x if he doesn't. He can also buy negative insurance, where Gaston pays $3x if he loses his sense of smell and gets $x if he doesn't. Gaston says, "Money will be only half as important to me if I lose my sense of smell." If we look at his expected utility function, we see what he means. Where c1 is his consumption if he retains his sense of smell and c2 is his income if he loses his sense of smell, Gaston has the expected utility function U(c1, c2) = 
. What insurance should he buy?
of losing his sense of smell, which would greatly reduce his enjoyment of food. Gaston finds an insurance company that will sell him insurance where Gaston gets $3x if he loses his smell and pays $x if he doesn't. He can also buy negative insurance, where Gaston pays $3x if he loses his sense of smell and gets $x if he doesn't. Gaston says, "Money will be only half as important to me if I lose my sense of smell." If we look at his expected utility function, we see what he means. Where c1 is his consumption if he retains his sense of smell and c2 is his income if he loses his sense of smell, Gaston has the expected utility function U(c1, c2) = . What insurance should he buy? سؤال
Every $1 invested in Safe Sox will yield $2 for sure. Each $1 invested in Wobbly Umbrellas will yield $8 with probability 
and $0 with probability 
. An investor has $10,000 to invest in these two companies and her von Neumann-Morgenstern utility function is the expected value of the natural logarithm of the total yield on her investments. If S is the amount of money that she invests in Safe Sox and $10,000 2 S is the amount that she invests in Wobbly Umbrellas, what should S be to maximize her expected utility? (Pick the closest answer.)
A) $1,111
B) $3,333
C) $5,000
D) $6,667
E) $9,111
and $0 with probability . An investor has $10,000 to invest in these two companies and her von Neumann-Morgenstern utility function is the expected value of the natural logarithm of the total yield on her investments. If S is the amount of money that she invests in Safe Sox and $10,000 2 S is the amount that she invests in Wobbly Umbrellas, what should S be to maximize her expected utility? (Pick the closest answer.)A) $1,111
B) $3,333
C) $5,000
D) $6,667
E) $9,111
فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/39
العب
ملء الشاشة (f)
Deck 11: Uncertainty
1
A consumer has a von Neumann-Morgenstern utility function of the form U(cA, cB, pA, pB) = pAv(cA) + pBv(cB), where pA and pB are the probabilities of events A and B and where cA and cB are consumptions contingent on events A and B respectively. This consumer must be a risk lover if v is an increasing function.
False
2
Prufrock is risk averse. He is offered a gamble in which with probability 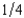he will lose $1,000 and with probability , he will win $500.
A) Since he is risk averse, he will certainly not take the gamble.
B) Since the expected value of the gamble is positive, he will certainly take the gamble.
C) If Prufrock's initial wealth is greater than $1,500, he will certainly take the gamble.
D) If Prufrock's initial wealth is smaller than $1,500, he will certainly not take the gamble.
E) Not enough information is given to determine for sure whether he will take the gamble.
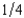he will lose $1,000 and with probability , he will win $500.A) Since he is risk averse, he will certainly not take the gamble.
B) Since the expected value of the gamble is positive, he will certainly take the gamble.
C) If Prufrock's initial wealth is greater than $1,500, he will certainly take the gamble.
D) If Prufrock's initial wealth is smaller than $1,500, he will certainly not take the gamble.
E) Not enough information is given to determine for sure whether he will take the gamble.
E
3
Ronald has $18,000. But he is forced to bet it on the flip of a fair coin. If he wins he has $36,000. If he loses he has nothing. Ronald's expected utility function is .5x.5 + .5y.5, where x is his wealth if heads comes up and y is his wealth if tails comes up. Since he must make this bet, he is exactly as well off as if he had a perfectly safe income of
A) $16,000.
B) $15,000.
C) $12,000.
D) $11,000.
E) $9,000.
A) $16,000.
B) $15,000.
C) $12,000.
D) $11,000.
E) $9,000.
E
4
Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 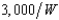), where W is his wealth. Buck's total wealth is $12,000. With probability .2 the palace will be a failure and he'll lose $9,000, so that his wealth will be just $3,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $12,000 with certainty?
A) $75,000
B) $14,250
C) $36,000
D) $48,000
E) $15,000
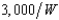), where W is his wealth. Buck's total wealth is $12,000. With probability .2 the palace will be a failure and he'll lose $9,000, so that his wealth will be just $3,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $12,000 with certainty?A) $75,000
B) $14,250
C) $36,000
D) $48,000
E) $15,000
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
5
Joe's wealth is $100 and he is an expected utility maximizer with a von Neumann-Morgenstern utility function 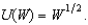Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?
A) $10
B) $15
C) $19
D) $100
E) $50
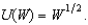Joe is afraid of oversleeping his economics exam. He figures there is only a 1 in 10 chance that he will, but if he does, it will cost him $100 in fees to the university for taking an exam late. Joe's neighbor, Mary, never oversleeps. She offers to wake him one hour before the test, but he must pay her for this service. What is the most that Joe would be willing to pay for this wake-up service?A) $10
B) $15
C) $19
D) $100
E) $50
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
6
Timmy Qualm's uncle gave him a lottery ticket. With probability 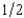the ticket will be worth $100 and with probability 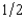it will be worthless. Let x be Timmy's wealth if the lottery ticket is a winner, and y his wealth if it is a loser. Timmy's preferences over alternative contingent commodity bundles are represented by the utility function U(x, y) = min{ 2x - y, 2y - x}. He has no risks other than the ticket.
A) Timmy would sell his lottery ticket for $25 but not for less.
B) Timmy hates risk so much that he'd be willing to throw away the lottery ticket rather than worry about whether he won.
C) Timmy satisfies the expected utility hypothesis.
D) Timmy is misnamed. He is a risk lover.
E) None of the above.
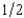the ticket will be worth $100 and with probability 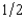it will be worthless. Let x be Timmy's wealth if the lottery ticket is a winner, and y his wealth if it is a loser. Timmy's preferences over alternative contingent commodity bundles are represented by the utility function U(x, y) = min{ 2x - y, 2y - x}. He has no risks other than the ticket.A) Timmy would sell his lottery ticket for $25 but not for less.
B) Timmy hates risk so much that he'd be willing to throw away the lottery ticket rather than worry about whether he won.
C) Timmy satisfies the expected utility hypothesis.
D) Timmy is misnamed. He is a risk lover.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
7
There are two events, 1 and 2. The probability of event 1 is p and the probability of event 2 is 1 - p. Sally Kink is an expected utility maximizer with a utility function is pu(c1) + (1 - p)u(c2), where for any number x, u(x) = 2x if x < 1,000 and u(x) = 1,000 + x if x is greater than or equal to 1,000.
A) Sally is a risk lover.
B) Sally will be a risk averter if she is poor but will be a risk lover if she is rich.
C) Sally will be a risk lover if she is poor but a risk averter if she is rich.
D) If there is no chance of her wealth exceeding $1,000, then she will take any bet that has positive expected net winnings.
E) None of the above.
A) Sally is a risk lover.
B) Sally will be a risk averter if she is poor but will be a risk lover if she is rich.
C) Sally will be a risk lover if she is poor but a risk averter if she is rich.
D) If there is no chance of her wealth exceeding $1,000, then she will take any bet that has positive expected net winnings.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
8
If the price of insurance goes up, people will become less risk averse.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
9
If Paul is risk loving and his basketball team has a probability of .5 of winning, then Paul would rather bet $10 on his team than $100. (When Paul bets X, he wins X if his team wins and loses X if his team loses.)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
10
Of any two gambles, no matter what their expected returns, a risk averter will choose the one with the smaller variance.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
11
Diego has $6,400. He plans to bet on a soccer game. Team A is a favorite to win. Assume no ties can occur. For $.80 one can buy a ticket that will pay $1 if team A wins and nothing if B wins. For $.20 one can buy a ticket that pays $1 if team B wins and nothing if A wins. Diego thinks the two teams are equally likely to win. He buys tickets so as to maximize the expected value of lnW (the natural log of his wealth). After he buys his tickets, team A loses a star player and the ticket price moves to $.50 for either team. Diego buys some new tickets and sells some of his old ones. The game is then played and team A wins. How much wealth does he end up with?
A) $5,000
B) $15,000
C) $6,400
D) $8,400
E) $10,000
A) $5,000
B) $15,000
C) $6,400
D) $8,400
E) $10,000
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
12
If someone has strictly convex preferences between all contingent commodity bundles, then he or she must be risk averse.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
13
Mabel and Emil were contemplating marriage. They got to talking. Mabel said that she always acted according to the expected utility hypothesis, where she tried to maximize the expected value of the log of her income. Emil said that he too was an expected utility maximizer, but he tried to maximize the expected value of the square of his income. Mabel said, "I fear we must part. Our attitudes toward risk are too different." Emil said, "Never fear, my dear, the square of income is a monotonic increasing function of the log of income, so we really have the same preferences." Who is right about whether their preferences toward risk are different?
A) Mabel is right.
B) Emil is right.
C) Emil is right about small risks but wrong about large risks.
D) Mabel is right about small risks but wrong about large risks.
E) They are both wrong.
A) Mabel is right.
B) Emil is right.
C) Emil is right about small risks but wrong about large risks.
D) Mabel is right about small risks but wrong about large risks.
E) They are both wrong.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
14
Oskar's preferences over gambles in which the probability of events 1 and 2 are both 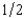can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income of
A) $12.5.
B) $9.
C) $16.
D) $17.
E) None of the above.
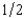can be represented by the von Neuman-Morgenstern utility function .5y.51 + .5y.52, where y1 is his consumption if event 1 happens and y2 is his consumption if event 2 happens. A gamble that allows him a consumption of $9 if event 1 happens and $25 if event 2 happens is exactly as good for Oskar as being sure to have an income ofA) $12.5.
B) $9.
C) $16.
D) $17.
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
15
Socrates owns just one ship. The ship is worth $200 million dollars. If the ship sinks, Socrates loses $200 million. The probability that it will sink is .02. Socrates' total wealth including the value of the ship is $225 million. He is an expected utility maximizer with von Neuman-Morgenstern utility U(W) equal to the square root of W. What is the maximum amount that Socrates would be willing to pay in order to be fully insured against the risk of losing his ship?
A) $4 million
B) $2 million
C) $3.84 million
D) $4.82 million
E) $5.96 million
A) $4 million
B) $2 million
C) $3.84 million
D) $4.82 million
E) $5.96 million
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
16
An expected utility maximizer's preferences between two bundles contingent on event 1 happening must be independent of what he will get if event 2 happens.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
17
Gary likes to gamble. Donna offers to bet him $70 on the outcome of a boat race. If Gary's boat wins, Donna would give him $70. If Gary's boat does not win, Gary would give her $70. Gary's utility function is U(c1, c2, p1, p2) = p1c21 + p2c21, where p1 and p2 are the probabilities of events 1 and 2 and where c1 and c2 are his consumption if events 1 and 2 occur respectively. Gary's total wealth is currently only $80 and he believes that the probability that he will win the race is .3.
A) Taking the bet would increase his expected utility.
B) Taking the bet would reduce his expected utility.
C) Taking the bet would leave his expected utility unchanged.
D) There is not enough information to determine whether taking the bet would increase or decrease his expected utility.
E) The information given in the problem is self-contradictory.
A) Taking the bet would increase his expected utility.
B) Taking the bet would reduce his expected utility.
C) Taking the bet would leave his expected utility unchanged.
D) There is not enough information to determine whether taking the bet would increase or decrease his expected utility.
E) The information given in the problem is self-contradictory.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
18
Clancy has $1,200. He plans to bet on a boxing match between Sullivan and Flanagan. For $4, he can buy a coupon that pays $10 if Sullivan wins and nothing otherwise. For $6 he can buy a coupon that will pay $10 if Flanagan wins and nothing otherwise. Clancy doesn't agree with these odds. He thinks that the two fighters each have a probability of 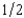of winning. If he is an expected utility maximizer who tries to maximize the expected value of lnW, where lnW is the natural log of his wealth, it would be rational for him to buy
A) 50 Sullivan coupons and no Flanagan coupons.
B) 100 Sullivan coupons and no Flanagan coupons.
C) 50 Flanagan coupons and no Sullivan coupons.
D) 100 Flanagan coupons and no Sullivan coupons.
E) 100 of each kind of coupon.
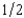of winning. If he is an expected utility maximizer who tries to maximize the expected value of lnW, where lnW is the natural log of his wealth, it would be rational for him to buyA) 50 Sullivan coupons and no Flanagan coupons.
B) 100 Sullivan coupons and no Flanagan coupons.
C) 50 Flanagan coupons and no Sullivan coupons.
D) 100 Flanagan coupons and no Sullivan coupons.
E) 100 of each kind of coupon.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
19
Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 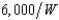), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?
A) $28,500
B) $150,000
C) $96,000
D) $72,000
E) $30,000
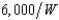), where W is his wealth. Buck's total wealth is $24,000. With probability .2 the palace will be a failure and he'll lose $18,000, so that his wealth will be just $6,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $24,000 with certainty?A) $28,500
B) $150,000
C) $96,000
D) $72,000
E) $30,000
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
20
Wilma is not risk averse. She is offered a chance to pay $10 for a lottery ticket that will give her a prize of $100 with probability .06, a prize of $50 with probability .1, and no prize with probability .85. If she understands the odds and makes no mistakes in calculation, she will buy the lottery ticket.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
21
Tom Cruiser's car is worth $100,000. But Tom is careless and leaves the top down and the keys in the ignition. Consequently his car will be stolen with probability .5. If it is stolen, he will never get it back. Tom has $100,000 in other wealth and his von Neumann-Morgenstern utility function for wealth is u(w) = ln(w). Suppose that Tom can buy $K worth of insurance at a price of $.6K. How much insurance will Tom buy?
A) $0
B) $100,000
C) More than $0 but less than $50,000
D) More than $50,000 but less than $100,000
E) Exactly $50,000
A) $0
B) $100,000
C) More than $0 but less than $50,000
D) More than $50,000 but less than $100,000
E) Exactly $50,000
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
22
Harley's current wealth is $600, but there is a .25 probability that he will lose $100. Harley is risk neutral. He has an opportunity to buy insurance that would restore his $100 if he lost it.
A) Harley would be willing to pay a bit more than $25 for this insurance.
B) Harley would be willing to pay up to $25 for this insurance.
C) Since Harley is risk neutral, he wouldn't be willing to pay anything for this insurance.
D) Since Harley's utility function is not specified, we can't tell how much he would be willing to pay for this insurance.
E) Harley would not be willing to pay more than $16.66 for this insurance.
A) Harley would be willing to pay a bit more than $25 for this insurance.
B) Harley would be willing to pay up to $25 for this insurance.
C) Since Harley is risk neutral, he wouldn't be willing to pay anything for this insurance.
D) Since Harley's utility function is not specified, we can't tell how much he would be willing to pay for this insurance.
E) Harley would not be willing to pay more than $16.66 for this insurance.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
23
Sally Kink is an expected utility maximizer with utility function pu(c1) + (1 - p)u(c2), where for any x < $3,000, u(x) = 2x, and for x greater than or equal to $3,000, u(x) = 3,0001 + x.
A) Sally will be risk averse if her income is less than $3,000 but risk loving if her income is more than $3,000.
B) Sally will be risk neutral if her income is less than $3,000 and risk averse if her income is more than $3,000.
C) For bets that involve no chance of her wealth exceeding $3,000, Sally will take any bet that has a positive expected net payoff.
D) Sally will never take a bet if there is a chance that it leaves her with wealth less than $6,000.
E) None of the above are true.
A) Sally will be risk averse if her income is less than $3,000 but risk loving if her income is more than $3,000.
B) Sally will be risk neutral if her income is less than $3,000 and risk averse if her income is more than $3,000.
C) For bets that involve no chance of her wealth exceeding $3,000, Sally will take any bet that has a positive expected net payoff.
D) Sally will never take a bet if there is a chance that it leaves her with wealth less than $6,000.
E) None of the above are true.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
24
Clancy has $1,800. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $9 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $1 each. Clancy believes that the two fighters each have a probability of 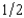of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?
A) Don't gamble at all.
B) Buy 100 Sullivan tickets and 900 Flanagan tickets.
C) Buy exactly as many Flanagan tickets as Sullivan tickets.
D) Buy 50 Sullivan tickets and 450 Flanagan tickets.
E) Buy 50 Sullivan tickets and 900 Flanagan tickets.
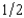of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?A) Don't gamble at all.
B) Buy 100 Sullivan tickets and 900 Flanagan tickets.
C) Buy exactly as many Flanagan tickets as Sullivan tickets.
D) Buy 50 Sullivan tickets and 450 Flanagan tickets.
E) Buy 50 Sullivan tickets and 900 Flanagan tickets.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
25
Linus Piecewise is an expected utility maximizer. There are two events, H and T, which each have probability 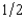. Linus's preferences over lotteries in which his wealth is h if event H happens and t if event T happens are representable by the utility function 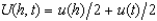. The function u takes the following form. For any x, u(x) = x if x < 100 and u(x) = 100 + 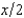if x is greater than or equal to 100. Draw a graph showing the indifference curves for Linus that pass through
a. the point (50, 0)
b. the point (50, 100)
c. the point (100, 100)
d. the point (150, 100)
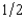. Linus's preferences over lotteries in which his wealth is h if event H happens and t if event T happens are representable by the utility function 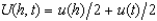. The function u takes the following form. For any x, u(x) = x if x < 100 and u(x) = 100 + 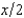if x is greater than or equal to 100. Draw a graph showing the indifference curves for Linus that pass through a. the point (50, 0)
b. the point (50, 100)
c. the point (100, 100)
d. the point (150, 100)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
26
Quincy's expected utility function is pc 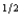1 + (1 - p)c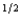
2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .60 and $12,100 with probability .40. Wilbur will choose the sure payment if
A) Z > 6,400 and the lottery if Z < 6,400.
B) Z > 12,100 and the lottery if Z < 12,100.
C) Z > 9,250 and the lottery if Z < 9,250.
D) Z > 5,000 and the lottery if Z < 5,000.
E) Z > 7,000 and the lottery if Z < 7,000.
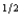1 + (1 - p)c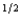 2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .60 and $12,100 with probability .40. Wilbur will choose the sure payment if
A) Z > 6,400 and the lottery if Z < 6,400.
B) Z > 12,100 and the lottery if Z < 12,100.
C) Z > 9,250 and the lottery if Z < 9,250.
D) Z > 5,000 and the lottery if Z < 5,000.
E) Z > 7,000 and the lottery if Z < 7,000.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
27
Willy's only source of wealth is his chocolate factory. He has the utility function pc 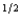f + (1 - p)c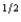
nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =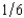 . The value of Willy's factory is $500,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy
A) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
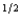f + (1 - p)c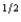 nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
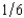. The value of Willy's factory is $500,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buyA) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
28
Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function 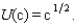If Billy is not injured this season, he will receive an income of $25 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is
A) 100,000.
B) 9,020.
C) between 24 million and 25 million.
D) 4,510.
E) 18,040.
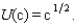If Billy is not injured this season, he will receive an income of $25 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility isA) 100,000.
B) 9,020.
C) between 24 million and 25 million.
D) 4,510.
E) 18,040.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
29
After graduating, Sallie Handshake's best job offer will either be with a Big-8 accounting firm for $160,000 a year or as a State Farm agent in Grand Rapids, Michigan, for $40,000 a year. She can increase the probability of the former outcome by studying more, but such studying has its costs. If S represents her amount of studying (where S = 0 is no study and S = 1 is all-out effort), her probability of getting the job with a Big-8 firm just equals S. Her utility depends on how hard she studies and her subsequent annual income Y. She tries to maximize the expected value of the von Neuman-Morgenstern utility function If she chooses S to maximize her expected utility, how much will she study?
A) S = 0.1.
B) S = 0.25.
C) S = 0.5.
D) S = 0.75.
E) S = 0.9.
If she chooses S to maximize her expected utility, how much will she study?A) S = 0.1.
B) S = 0.25.
C) S = 0.5.
D) S = 0.75.
E) S = 0.9.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
30
The certainty equivalent of a gamble is defined to be the amount of money which, if you were promised it with certainty, would be indifferent to the gamble.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W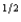
(where W is wealth) and if the probability of events 1 and 2 are both , write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens.
b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
a. If an expected utility maximizer has a von Neuman-Morgenstern utility function U(W) = W
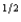
(where W is wealth) and if the probability of events 1 and 2 are both
, write a formula for the certainty equivalent of a gamble that gives you x if event 1 happens and y if event 2 happens. b. Generalize your formula in part (a) to the case where the probability of event 1 is p and the probability of event 2 is 1 - p.
c. Generalize the formula in part (a) to the case where U(W) = Wa for a > 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
31
Oliver takes his wealth of $1,000 to a casino. He can bet as much as he likes on the toss of a coin but the "house" takes a cut. If Oliver bets $x on heads, then if heads comes up, he gets $.8x and, if tails comes up, he pays $x. Similarly if he bets $x on tails and if tails comes up, he wins $.8x and, if heads comes up, he pays $x. Draw a graph with dollars contingent on heads and dollars contingent on tails on the two axes. Show Oliver's budget constraint. Oliver is an expected utility maximizer with the utility function 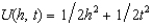, where h is his wealth if heads comes up and t is his wealth if tails comes up. Draw the highest indifference curve that Oliver can reach with his budget. What bets if any does he make?
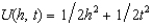, where h is his wealth if heads comes up and t is his wealth if tails comes up. Draw the highest indifference curve that Oliver can reach with his budget. What bets if any does he make? فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
32
Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function If Billy is not injured this season, he will receive an income of $16 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is
A) 3,610.
B) between 15 million and 16 million.
C) 100,000.
D) 7,220.
E) 14,440.
If Billy is not injured this season, he will receive an income of $16 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility isA) 3,610.
B) between 15 million and 16 million.
C) 100,000.
D) 7,220.
E) 14,440.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
33
Willy's only source of wealth is his chocolate factory. He has the utility function pc 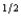f + (1 - p)c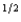
nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =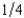 . The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 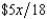whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy
A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance his wealth will beof what it would be if there were no flood.
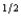f + (1 - p)c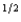 nf, where p is the probability of a flood, 1 - p is the probability of no flood, and cf and cnf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p =
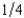. The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 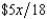whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buyA) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
E) enough insurance so that if there is a flood, after he collects his insurance his wealth will beof what it would be if there were no flood.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
34
Clancy has $5,000. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $5 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $5 each. Clancy believes that the two fighters each have a probability of 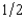of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?
A) Buy exactly as many Flanagan tickets as Sullivan tickets.
B) Buy 250 Sullivan tickets and 250 Flanagan tickets.
C) Don't gamble at all.
D) Buy 500 Sullivan tickets and 500 Flanagan tickets.
E) Buy 250 Sullivan tickets and 500 Flanagan tickets.
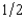of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?A) Buy exactly as many Flanagan tickets as Sullivan tickets.
B) Buy 250 Sullivan tickets and 250 Flanagan tickets.
C) Don't gamble at all.
D) Buy 500 Sullivan tickets and 500 Flanagan tickets.
E) Buy 250 Sullivan tickets and 500 Flanagan tickets.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
35
Yoram's expected utility function is pc 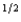1 + (1 - p)c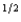
2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
A) Z > 3,249 and the lottery if Z < 3,249.
B) Z > 2,874.50 and the lottery if Z < 2,874.50.
C) Z > 3,600 and the lottery if Z < 3,600.
D) Z > 3,424.50 and the lottery if Z < 3,424.50.
E) Z > 3,270 and the lottery if Z < 3,270.
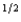1 + (1 - p)c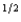 2, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $2,500 with probability .30 and $3,600 with probability .70. Wilbur will choose the sure payment if
A) Z > 3,249 and the lottery if Z < 3,249.
B) Z > 2,874.50 and the lottery if Z < 2,874.50.
C) Z > 3,600 and the lottery if Z < 3,600.
D) Z > 3,424.50 and the lottery if Z < 3,424.50.
E) Z > 3,270 and the lottery if Z < 3,270.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
36
Sally Kink is an expected utility maximizer with utility function pu(c1) + (1 - p)u(c2), where for any x < $2,000, u(x) = 2x, and for x greater than or equal to $2,000, u(x) = 2,000 + x.
A) For bets that involve no chance of her wealth exceeding $2,000, Sally will take any bet that has a positive expected net payoff.
B) Sally will be risk averse if her income is less than $2,000 but risk loving if her income is more than $2,000.
C) Sally will be risk neutral if her income is less than $2,000 and risk averse if her income is more than $2,000.
D) Sally will never take a bet if there is a chance that it leaves her with wealth less than $4,000.
E) None of the above are true.
A) For bets that involve no chance of her wealth exceeding $2,000, Sally will take any bet that has a positive expected net payoff.
B) Sally will be risk averse if her income is less than $2,000 but risk loving if her income is more than $2,000.
C) Sally will be risk neutral if her income is less than $2,000 and risk averse if her income is more than $2,000.
D) Sally will never take a bet if there is a chance that it leaves her with wealth less than $4,000.
E) None of the above are true.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
37
Portia has waited a long time for her ship to come in, and she has concluded that it will arrive today with probability 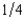. If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?
A) $1
B) $2
C) $2.50
D) $4
E) None of the above.
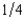. If it does come, she will receive $16. If it doesn't come in today, it never will and she will have zero wealth. She has a von Neumann-Morgenstern utility function equal to the square root of her total income. What is the minimum price at which she would sell the rights to her ship?A) $1
B) $2
C) $2.50
D) $4
E) None of the above.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
38
Gaston Gourmand loves good food. Due to an unusual ailment, he has a probability of 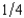of losing his sense of smell, which would greatly reduce his enjoyment of food. Gaston finds an insurance company that will sell him insurance where Gaston gets $3x if he loses his smell and pays $x if he doesn't. He can also buy negative insurance, where Gaston pays $3x if he loses his sense of smell and gets $x if he doesn't. Gaston says, "Money will be only half as important to me if I lose my sense of smell." If we look at his expected utility function, we see what he means. Where c1 is his consumption if he retains his sense of smell and c2 is his income if he loses his sense of smell, Gaston has the expected utility function U(c1, c2) = 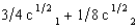. What insurance should he buy?
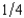of losing his sense of smell, which would greatly reduce his enjoyment of food. Gaston finds an insurance company that will sell him insurance where Gaston gets $3x if he loses his smell and pays $x if he doesn't. He can also buy negative insurance, where Gaston pays $3x if he loses his sense of smell and gets $x if he doesn't. Gaston says, "Money will be only half as important to me if I lose my sense of smell." If we look at his expected utility function, we see what he means. Where c1 is his consumption if he retains his sense of smell and c2 is his income if he loses his sense of smell, Gaston has the expected utility function U(c1, c2) = 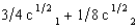. What insurance should he buy? فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
39
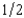Every $1 invested in Safe Sox will yield $2 for sure. Each $1 invested in Wobbly Umbrellas will yield $8 with probability and $0 with probability . An investor has $10,000 to invest in these two companies and her von Neumann-Morgenstern utility function is the expected value of the natural logarithm of the total yield on her investments. If S is the amount of money that she invests in Safe Sox and $10,000 2 S is the amount that she invests in Wobbly Umbrellas, what should S be to maximize her expected utility? (Pick the closest answer.)
A) $1,111
B) $3,333
C) $5,000
D) $6,667
E) $9,111
and $0 with probability 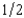. An investor has $10,000 to invest in these two companies and her von Neumann-Morgenstern utility function is the expected value of the natural logarithm of the total yield on her investments. If S is the amount of money that she invests in Safe Sox and $10,000 2 S is the amount that she invests in Wobbly Umbrellas, what should S be to maximize her expected utility? (Pick the closest answer.)A) $1,111
B) $3,333
C) $5,000
D) $6,667
E) $9,111
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
فتح الحزمة
k this deck
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 39 في هذه المجموعة.
