Deck 19: Linear Programming
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/105
العب
ملء الشاشة (f)
Deck 19: Linear Programming
1
Graphical linear programming can handle problems that involve any number of decision variables.
False
2
The equation 5x + 7y = 10 is linear.
True
3
LP problems must have a single goal or objective specified.
True
4
An objective function represents a family of parallel lines.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
5
The term "iso-profit" line means that all points on the line will yield the same profit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
6
A maximization problem may be characterized by all greater than or equal to constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
7
A change in the value of an objective function coefficient does not change the optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
8
Linear programming techniques will always produce an optimal solution to an LP problem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
9
The term "range of optimality" refers to a constraint's right-hand side quantity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
10
A linear programming problem can have multiple optimal solutions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
11
The term "range of feasibility" refers to coefficients of the objective function.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
12
The value of an objective function decreases as it is moved away from the origin.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
13
A shadow price indicates how much a one-unit decrease/increase in the right-hand side value of a constraint will decrease/increase the optimal value of the objective function.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
14
If a single optimal solution exists to a graphical LP problem, it will exist at a corner point.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
15
The equation 3xy = 9 is linear.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
16
An example of a decision variable in an LP problem is profit maximization.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
17
Constraints limit the alternatives available to a decision-maker, removing constraints adds viable alternative solutions.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
18
The feasible solution space only contains points that satisfy all constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
19
The feasible solution space is the set of all feasible combinations of decision variables as defined by only binding constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
20
The simplex method is a general-purpose LP algorithm that can be used for solving only problems with more than six variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
21
The linear optimization technique for allocating constrained resources among different products is:
A)linear regression analysis
B)linear disaggregation
C)linear decomposition
D)linear programming
E)linear tracking analysis
A)linear regression analysis
B)linear disaggregation
C)linear decomposition
D)linear programming
E)linear tracking analysis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
22
Non-binding constraints are not associated with the feasible solution space; i.e., they are redundant and can be eliminated from the matrix.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
23
Coordinates of all corner points are substituted into the objective function when we use the approach called:
A)Least Squares
B)Regression
C)Enumeration
D)Graphical Linear Programming
E)Constraint Assignment
A)Least Squares
B)Regression
C)Enumeration
D)Graphical Linear Programming
E)Constraint Assignment

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
24
Every change in the value of an objective function coefficient will lead to changes in the optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
25
The logical approach, from beginning to end, for assembling a linear programming model begins with:
A)identifying the decision variables
B)identifying the objective function
C)specifying the objective function parameters
D)identifying the constraints
E)specifying the constraint parameters
A)identifying the decision variables
B)identifying the objective function
C)specifying the objective function parameters
D)identifying the constraints
E)specifying the constraint parameters

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
26
Which of the following could not be a linear programming problem constraint?
A)1A + 2B 3
B)1A + 2B 3
C)1A + 2B = 3
D)1A + 2B + 3C + 4D 5
E)1 A + 2B
A)1A + 2B 3
B)1A + 2B 3
C)1A + 2B = 3
D)1A + 2B + 3C + 4D 5
E)1 A + 2B

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
27
When a change in the value of an objective function coefficient remains within the range of optimality, the optimal solution would also remain the same.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
28
Non-zero slack or surplus is associated with a binding constraint.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
29
In graphical linear programming, when the objective function is parallel to one of the binding constraints, then:
A)the solution is sub-optimal
B)multiple optimal solutions exist
C)a single corner point solution exists
D)no feasible solution exists
E)the constraint must be changed or eliminated
A)the solution is sub-optimal
B)multiple optimal solutions exist
C)a single corner point solution exists
D)no feasible solution exists
E)the constraint must be changed or eliminated

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
30
In graphical linear programming the objective function is:
A)linear
B)a family of parallel lines
C)a family of iso-profit lines
D)all of the above
E)none of the above
A)linear
B)a family of parallel lines
C)a family of iso-profit lines
D)all of the above
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
31
Which of the choices below constitutes a simultaneous solution to these equations? 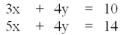
A)x = 2, y = .5
B)x = 4, y = -.5
C)x = 2, y = 1
D)x = y
E)y = 2x
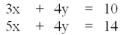
A)x = 2, y = .5
B)x = 4, y = -.5
C)x = 2, y = 1
D)x = y
E)y = 2x

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
32
Using the enumeration approach, optimality is obtained by evaluating every coordinate.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
33
Which of the choices below constitutes a simultaneous solution to these equations? 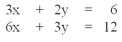
A)x = 1, y = 1.5
B)x = .5, y = 2
C)x = 0, y = 3
D)x = 2, y = 0
E)x = 0, y = 0
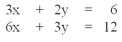
A)x = 1, y = 1.5
B)x = .5, y = 2
C)x = 0, y = 3
D)x = 2, y = 0
E)x = 0, y = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
34
What combination of x and y will yield the optimum for this problem? 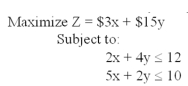
A)x = 2, y = 0
B)x = 0, y = 0
C)x = 0, y = 3
D)x = 1, y = 5
E)none of the above
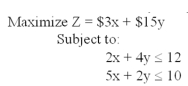
A)x = 2, y = 0
B)x = 0, y = 0
C)x = 0, y = 3
D)x = 1, y = 5
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
35
For the products A, B, C and D, which of the following could be a linear programming objective function?
A)Z = 1A + 2B + 3C + 4D
B)Z = 1A + 2BC + 3D
C)Z = 1A + 2AB + 3ABC + 4ABCD
D)Z = 1A + 2B/C + 3D
E)all of the above
A)Z = 1A + 2B + 3C + 4D
B)Z = 1A + 2BC + 3D
C)Z = 1A + 2AB + 3ABC + 4ABCD
D)Z = 1A + 2B/C + 3D
E)all of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
36
Which of the following is not a component of the structure of a linear programming model?
A)Constraints
B)Decision variables
C)Parameters
D)A goal or objective
E)Environmental uncertainty
A)Constraints
B)Decision variables
C)Parameters
D)A goal or objective
E)Environmental uncertainty

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
37
Which objective function has the same slope as this one: $4x + $2y = $20?
A)$4x + $2y = $10
B)$2x + $4y = $20
C)$2x - $4y = $20
D)$4x - $2y = $20
E)$8x + $8y = $20
A)$4x + $2y = $10
B)$2x + $4y = $20
C)$2x - $4y = $20
D)$4x - $2y = $20
E)$8x + $8y = $20

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
38
The region which satisfies all of the constraints in graphical linear programming is called the:
A)optimum solution space
B)region of optimality
C)lower left hand quadrant
D)region of non-negativity
E)feasible solution space
A)optimum solution space
B)region of optimality
C)lower left hand quadrant
D)region of non-negativity
E)feasible solution space

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
39
In the range of feasibility, the value of the shadow price remains constant.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
40
For the constraints given below, which point is in the feasible solution space of this maximization problem? 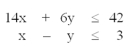
A)x = 1, y = 5
B)x = -1, y = 1
C)x = 4, y = 4
D)x = 2, y = 1
E)x = 2, y = 8
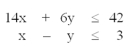
A)x = 1, y = 5
B)x = -1, y = 1
C)x = 4, y = 4
D)x = 2, y = 1
E)x = 2, y = 8

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
41
What is the objective function?
A)$1 A + $2 B = Z
B)$12 A + $8 B = Z
C)$2 A + $1 B = Z
D)$8 A + $12 B = Z
E)$4 A + $8 B = Z
A)$1 A + $2 B = Z
B)$12 A + $8 B = Z
C)$2 A + $1 B = Z
D)$8 A + $12 B = Z
E)$4 A + $8 B = Z

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
42
Consider the linear programming problem below: 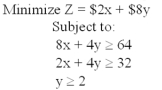 Determine the optimum amounts of x and y in terms of cost minimization.What is the minimum cost?
Determine the optimum amounts of x and y in terms of cost minimization.What is the minimum cost?
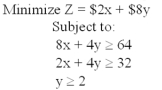 Determine the optimum amounts of x and y in terms of cost minimization.What is the minimum cost?
Determine the optimum amounts of x and y in terms of cost minimization.What is the minimum cost?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
43
The theoretical limit on the number of decision variables that can be handled by the simplex method in a single problem is:
A)1
B)2
C)3
D)4
E)unlimited
A)1
B)2
C)3
D)4
E)unlimited

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
44
A shadow price reflects which of the following in a maximization problem?
A)marginal cost of adding additional resources
B)marginal gain in the objective that would be realized by adding one unit of a resource
C)net gain in the objective that would be realized by adding one unit of a resource
D)marginal gain in the objective that would be realized by subtracting one unit of a resource
E)expected value of perfect information
A)marginal cost of adding additional resources
B)marginal gain in the objective that would be realized by adding one unit of a resource
C)net gain in the objective that would be realized by adding one unit of a resource
D)marginal gain in the objective that would be realized by subtracting one unit of a resource
E)expected value of perfect information

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
45
In linear programming, a non-zero reduced cost is associated with a:
A)decision variable in the solution
B)decision variable not in the solution
C)constraint for which there is slack
D)constraint for which there is surplus
E)constraint for which there is no slack or surplus
A)decision variable in the solution
B)decision variable not in the solution
C)constraint for which there is slack
D)constraint for which there is surplus
E)constraint for which there is no slack or surplus

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
46
Consider the following linear programming problem: 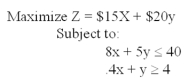 Solve the values of x and y that will maximize revenue.What revenue will result?
Solve the values of x and y that will maximize revenue.What revenue will result?
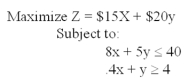 Solve the values of x and y that will maximize revenue.What revenue will result?
Solve the values of x and y that will maximize revenue.What revenue will result?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
47
What is the Dominican bean constraint?
A)12A + 8B 4,800
B)8A + 12B 4,800
C)4A + 8B 3,200
D)8A + 4B 3,200
E)4A + 8B 4,800
A)12A + 8B 4,800
B)8A + 12B 4,800
C)4A + 8B 3,200
D)8A + 4B 3,200
E)4A + 8B 4,800

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
48
The theoretical limit on the number of constraints that can be handled by the simplex method in a single problem is:
A)1
B)2
C)3
D)4
E)unlimited
A)1
B)2
C)3
D)4
E)unlimited

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
49
What are optimal weekly profits?
A)$0
B)$400
C)$700
D)$800
E)$900
A)$0
B)$400
C)$700
D)$800
E)$900

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
50
In linear programming, sensitivity analysis is associated with: (I) objective function coefficient
(II) right-hand side values of constraints
(III) constraint coefficient
A)I and II
B)II and III
C)I, II and III
D)I and III
E)none of the above
(II) right-hand side values of constraints
(III) constraint coefficient
A)I and II
B)II and III
C)I, II and III
D)I and III
E)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
51
A constraint that does not form a unique boundary of the feasible solution space is a:
A)redundant constraint
B)binding constraint
C)non-binding constraint
D)feasible solution constraint
E)constraint that equals zero
A)redundant constraint
B)binding constraint
C)non-binding constraint
D)feasible solution constraint
E)constraint that equals zero

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
52
What combination of x and y will provide a minimum for this problem? 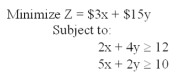
A)x = 0, y = 0
B)x = 0, y = 3
C)x = 0, y = 5
D)x = 1, y = 2.5
E)x = 6, y = 0
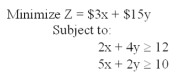
A)x = 0, y = 0
B)x = 0, y = 3
C)x = 0, y = 5
D)x = 1, y = 2.5
E)x = 6, y = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
53
Solve the following linear programming problem: 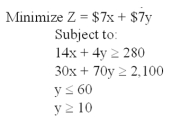
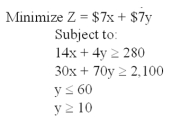

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
54
Which of the following is not a feasible production combination?
A)0 A & 0 B
B)0 A & 400 B
C)200 A & 300 B
D)400 A & 0 B
E)400 A & 400 B
A)0 A & 0 B
B)0 A & 400 B
C)200 A & 300 B
D)400 A & 0 B
E)400 A & 400 B

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
55
Given this problem: 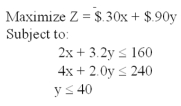
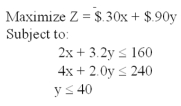

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
56
For the constraints given below, which point is in the feasible solution space of this minimization problem? 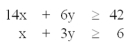
A)x = 0.5, y = 5.0
B)x = 0.0, y = 4.0
C)x = 2.0, y = 5.0
D)x = 1.0, y = 2.0
E)x = 2.0, y = 1.0
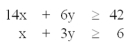
A)x = 0.5, y = 5.0
B)x = 0.0, y = 4.0
C)x = 2.0, y = 5.0
D)x = 1.0, y = 2.0
E)x = 2.0, y = 1.0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
57
What is the Columbia bean constraint?
A)1 A + 2 B 4,800
B)12 A + 8 B 4,800
C)2 A + 1 B 4,800
D)8 A + 12 B 4,800
E)4 A + 8 B 4,800
A)1 A + 2 B 4,800
B)12 A + 8 B 4,800
C)2 A + 1 B 4,800
D)8 A + 12 B 4,800
E)4 A + 8 B 4,800

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
58
A manager must decide on the mix of products to produce for the coming week.Product A requires three minutes per unit for molding, two minutes per unit for painting, and one minute per unit for packing.Product B requires two minutes per unit for molding, four minutes per unit for painting, and three minutes per unit for packing.There will be 600 minutes available for molding, 600 minutes for painting, and 420 minutes for packing.Both products have profits of $1.50 per unit.
(A) What combination of A and B will maximize profit?
(B) What is the maximum possible profit?
(C) How much of each resource will be unused for your solution?
(A) What combination of A and B will maximize profit?
(B) What is the maximum possible profit?
(C) How much of each resource will be unused for your solution?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
59
A small firm makes three products, which all follow the same three step process, which consists of milling, inspection, and drilling.Product A requires 6 minutes of milling, 5 minutes of inspection, and 4 minutes of drilling; product B requires 2.5 minutes of milling, 2 minutes of inspection, and 2 minutes of drilling; and product C requires 5 minutes of milling, 4 minutes of inspection, and 8 minutes of drilling.The department has 20 hours available during the next period for milling, 15 hours for inspection, and 24 hours for drilling.Product A contributes $6.00 per unit to profit, product B contributes $4.00 per unit, and product C contributes $10.00 per unit.
Use the following computer output to find the optimum mix of products in terms of maximizing contributions to profits for the next period.
PROBLEM TITLE: LINEAR PROGRAMMING
PROBLEM IS A MAX WITH 3 VARIABLES AND 3 CONSTRAINTS.


Use the following computer output to find the optimum mix of products in terms of maximizing contributions to profits for the next period.
PROBLEM TITLE: LINEAR PROGRAMMING
PROBLEM IS A MAX WITH 3 VARIABLES AND 3 CONSTRAINTS.




فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
60
For the production combination of 0 American and 400 British, which resource is "slack" (not fully used)?
A)Colombian beans (only)
B)Dominican beans (only)
C)both Colombian beans and Dominican beans
D)neither Colombian beans nor Dominican beans
E)cannot be determined exactly
A)Colombian beans (only)
B)Dominican beans (only)
C)both Colombian beans and Dominican beans
D)neither Colombian beans nor Dominican beans
E)cannot be determined exactly

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
61
What are optimal weekly profits?
A)$10,000
B)$4,600
C)$2,500
D)$5,200
E)$6,400
A)$10,000
B)$4,600
C)$2,500
D)$5,200
E)$6,400

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
62
What is the time constraint?
A)2 L + 3 D 480
B)2 L + 4 D 480
C)3 L + 2 D 480
D)4 L + 2 D 480
E)5 L + 3 D 480
A)2 L + 3 D 480
B)2 L + 4 D 480
C)3 L + 2 D 480
D)4 L + 2 D 480
E)5 L + 3 D 480

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
63
For the production combination of 1,400 A-100's and 900 B-200's which resource is "slack" (not fully used)?
A)circuit boards (only)
B)assembly time (only)
C)both circuit boards and assembly time
D)neither circuit boards nor assembly time
E)cannot be determined exactly
A)circuit boards (only)
B)assembly time (only)
C)both circuit boards and assembly time
D)neither circuit boards nor assembly time
E)cannot be determined exactly

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
64
Which of the following is not a feasible production combination?
A)0 L & 0 D
B)0 L & 120 D
C)90 L & 75 D
D)135 L & 0 D
E)135 L & 120 D
A)0 L & 0 D
B)0 L & 120 D
C)90 L & 75 D
D)135 L & 0 D
E)135 L & 120 D

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
65
Which of the following is not a feasible production combination?
A)0 B & 0 C
B)0 B & 1,100 C
C)800 B & 600 C
D)1,100 B & 0 C
E)0 B & 1,400 C
A)0 B & 0 C
B)0 B & 1,100 C
C)800 B & 600 C
D)1,100 B & 0 C
E)0 B & 1,400 C

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
66
What is the objective function?
A)$2 L + $3 D = Z
B)$2 L + $4 D = Z
C)$3 L + $2 D = Z
D)$4 L + $2 D = Z
E)$5 L + $3 D = Z
A)$2 L + $3 D = Z
B)$2 L + $4 D = Z
C)$3 L + $2 D = Z
D)$4 L + $2 D = Z
E)$5 L + $3 D = Z

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
67
What is the objective function?
A)$0.30 B + $0.20 C = Z
B)$0.60 B + $0.30 C = Z
C)$0.20 B + $0.30 C = Z
D)$0.20 B + $0.40 C = Z
E)$0.10 B + $0.10 C = Z
A)$0.30 B + $0.20 C = Z
B)$0.60 B + $0.30 C = Z
C)$0.20 B + $0.30 C = Z
D)$0.20 B + $0.40 C = Z
E)$0.10 B + $0.10 C = Z

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
68
For the production combination of 180 Root beer and 0 Sassafras soda, which resource is "slack" (not fully used)?
A)production time (only)
B)carbonated water (only)
C)both production time and carbonated water
D)neither production time and carbonated water
E)cannot be determined exactly
A)production time (only)
B)carbonated water (only)
C)both production time and carbonated water
D)neither production time and carbonated water
E)cannot be determined exactly

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
69
Which of the following is not a feasible production combination?
A)0 R & 0 S
B)0 R & 240 S
C)180 R & 120 S
D)300 R & 0 S
E)180 R & 240 S
A)0 R & 0 S
B)0 R & 240 S
C)180 R & 120 S
D)300 R & 0 S
E)180 R & 240 S

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
70
What is the assembly time constraint (in hours)?
A)1 A + 1 B 800
B)0.25 A + 0.5 B 800
C)0.5 A + 0.25 B 800
D)1 A + 0.5 B 800
E)0.25 A + 1 B 800
A)1 A + 1 B 800
B)0.25 A + 0.5 B 800
C)0.5 A + 0.25 B 800
D)1 A + 0.5 B 800
E)0.25 A + 1 B 800

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
71
What is the objective function?
A)$4.00 A + $1.00 B = Z
B)$0.25 A + $1.00 B = Z
C)$1.00 A + $4.00 B = Z
D)$1.00 A + $1.00 B = Z
E)$0.25 A + $0.50 B = Z
A)$4.00 A + $1.00 B = Z
B)$0.25 A + $1.00 B = Z
C)$1.00 A + $4.00 B = Z
D)$1.00 A + $1.00 B = Z
E)$0.25 A + $0.50 B = Z

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
72
What are optimal profits for today's production run?
A)$580
B)$340
C)$220
D)$380
E)$420
A)$580
B)$340
C)$220
D)$380
E)$420

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
73
What is the production time constraint (in minutes)?
A)2 R + 3 S 720
B)2 R + 5 S 720
C)3 R + 2 S 720
D)3 R + 5 S 720
E)5 R + 5 S 720
A)2 R + 3 S 720
B)2 R + 5 S 720
C)3 R + 2 S 720
D)3 R + 5 S 720
E)5 R + 5 S 720

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
74
For the production combination of 600 bagels and 800 croissants, which resource is "slack" (not fully used)?
A)flour (only)
B)sugar (only)
C)flour and yeast
D)flour and sugar
E)yeast and sugar
A)flour (only)
B)sugar (only)
C)flour and yeast
D)flour and sugar
E)yeast and sugar

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
75
For the production combination of 135 Lite and 0 Dark which resource is "slack" (not fully used)?
A)time (only)
B)malt extract (only)
C)both time and malt extract
D)neither time nor malt extract
E)cannot be determined exactly
A)time (only)
B)malt extract (only)
C)both time and malt extract
D)neither time nor malt extract
E)cannot be determined exactly

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
76
Which of the following is not a feasible production/sales combination?
A)0 A & 0 B
B)0 A & 1,000 B
C)1,800 A & 700 B
D)2,500 A & 0 B
E)100 A & 1,600 B
A)0 A & 0 B
B)0 A & 1,000 B
C)1,800 A & 700 B
D)2,500 A & 0 B
E)100 A & 1,600 B

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
77
What are optimal daily profits?
A)$0
B)$240
C)$420
D)$405
E)$505
A)$0
B)$240
C)$420
D)$405
E)$505

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
78
What are optimal daily profits?
A)$960
B)$1,560
C)$1,800
D)$1,900
E)$2,520
A)$960
B)$1,560
C)$1,800
D)$1,900
E)$2,520

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
79
What is the sugar constraint (in tablespoons)?
A)6 B + 3 C 4,800
B)1 B + 1 C 4,800
C)2 B + 4 C 4,800
D)4 B + 2 C 4,800
E)2 B + 3 C 4,800
A)6 B + 3 C 4,800
B)1 B + 1 C 4,800
C)2 B + 4 C 4,800
D)4 B + 2 C 4,800
E)2 B + 3 C 4,800

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck
80
What is the objective function?
A)$4 R + $6 S = Z
B)$2 R + $3 S = Z
C)$6 R + $4 S = Z
D)$3 R + $2 S = Z
E)$5 R + $5 S = Z
A)$4 R + $6 S = Z
B)$2 R + $3 S = Z
C)$6 R + $4 S = Z
D)$3 R + $2 S = Z
E)$5 R + $5 S = Z

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 105 في هذه المجموعة.
فتح الحزمة
k this deck








