Deck 11: Dynamic Programming
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/5
العب
ملء الشاشة (f)
Deck 11: Dynamic Programming
1
The management of a company is considering three possible new products for next year's product line.A decision now needs to be made regarding which products to market and at what production levels.Initiating the production of two of these products would require a substantial start-up cost,as shown in the first row of the table below.Once production is under way,the marginal net revenue from each unit produced is shown in the second row.The third row gives the percentage of the available production capacity that would be used for each unit produced. 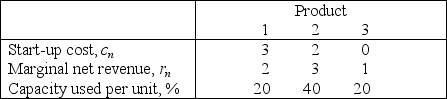 Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.
Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.
 Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.
Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.Since the decisions to be made are xn = production level of product n,for n = 1,2,3,the stages for a dynamic programming formulation of this problem correspond to the three products.When making the decision for a particular product,the essential information is the amount of production capacity still remaining,so this becomes the current state in this formulation.(a)At stage n,let the state sn be measured as the number of 20% blocks of production capacity still available for use on the remaining products,so the possible values of sn are 0,1,2,3,4,5,where s1 = 5,s2 = 5 - x1,and s3 = s2 - 2x2.Using the cn and rn values given in the above table,the profit from producing xn units of product n is easily calculated as pn(xn)= rnxn - cn,for n = 1,2,3.Therefore,using the usual dynamic programming notation presented in Sec.11.2 of the textbook,we have 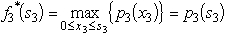 ,
, 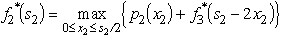 ,
, 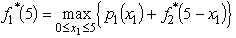 .Using these expressions for
.Using these expressions for 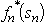 for n = 3,then n = 2,and then n = 1 in turn,the dynamic programming calculations are given below.For n = 3,
for n = 3,then n = 2,and then n = 1 in turn,the dynamic programming calculations are given below.For n = 3, 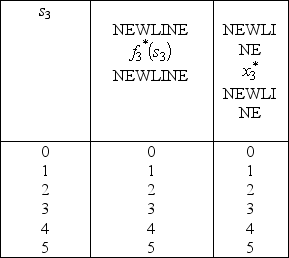 For n = 2,
For n = 2,  For n = 1,
For n = 1, 
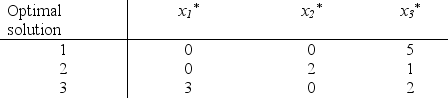 (b)Now production quantities are treated as continuous variables.Let sn be the percentage of the capacity left for the remaining products.(Note that the units of sn now are different than in part (a),so the possible values of sn now are 0 ≤ sn ≤ 100 rather than 0,1,2,3,4,5.)We now have s1 = 100,s2 = 100 -20x1,and s3 = s2 - 40x2.For product 3:
(b)Now production quantities are treated as continuous variables.Let sn be the percentage of the capacity left for the remaining products.(Note that the units of sn now are different than in part (a),so the possible values of sn now are 0 ≤ sn ≤ 100 rather than 0,1,2,3,4,5.)We now have s1 = 100,s2 = 100 -20x1,and s3 = s2 - 40x2.For product 3: 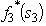 = s3 /20,with
= s3 /20,with 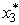 = s3 /20.For product 2:
= s3 /20.For product 2: 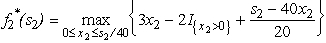 ,where
,where 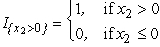 .This is linear in x2 except for the
.This is linear in x2 except for the 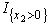 term.Therefore,we only need to examine the endpoints of the range for x2. If x2 = 0,we get
term.Therefore,we only need to examine the endpoints of the range for x2. If x2 = 0,we get 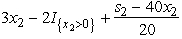 = s2 /20.If x2 = s2 /40,we get
= s2 /20.If x2 = s2 /40,we get 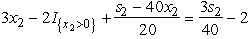 .Equating these two quantities,the breakpoint is s2 =80.So,
.Equating these two quantities,the breakpoint is s2 =80.So, 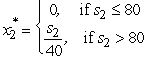 and
and 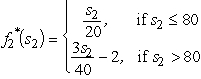 .For product 1:
.For product 1: 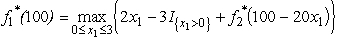 ,where
,where 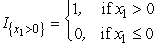 .Again,this is linear in x1 except for the
.Again,this is linear in x1 except for the 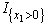 term.Therefore,we only need to examine the endpoints of the range for x1. If x1 = 0,we get
term.Therefore,we only need to examine the endpoints of the range for x1. If x1 = 0,we get 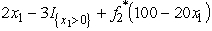 = 5.5.If x1 = 3,we get
= 5.5.If x1 = 3,we get 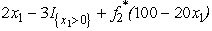 = 6 - 3 +
= 6 - 3 + 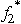 (40)= 5.So,
(40)= 5.So, 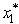 = 0 and
= 0 and 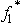 (100)= 5.5.With
(100)= 5.5.With 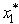 = 0,the state at stage 2 becomes s2 = 100,which leads to
= 0,the state at stage 2 becomes s2 = 100,which leads to 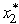 = 2.5 and s3 = 0,so
= 2.5 and s3 = 0,so 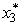 = 0.Therefore,the optimal solution is to produce 2.5 units of product 2,but none of products 1 and 3,with a profit of 5.5.This is better than with the integer restriction in part (a),as we would expect.
= 0.Therefore,the optimal solution is to produce 2.5 units of product 2,but none of products 1 and 3,with a profit of 5.5.This is better than with the integer restriction in part (a),as we would expect.
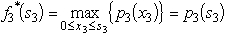 ,
, 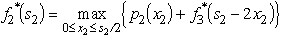 ,
, 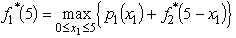 .Using these expressions for
.Using these expressions for  for n = 3,then n = 2,and then n = 1 in turn,the dynamic programming calculations are given below.For n = 3,
for n = 3,then n = 2,and then n = 1 in turn,the dynamic programming calculations are given below.For n = 3,  For n = 2,
For n = 2,  For n = 1,
For n = 1, 
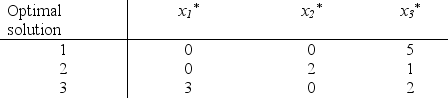 (b)Now production quantities are treated as continuous variables.Let sn be the percentage of the capacity left for the remaining products.(Note that the units of sn now are different than in part (a),so the possible values of sn now are 0 ≤ sn ≤ 100 rather than 0,1,2,3,4,5.)We now have s1 = 100,s2 = 100 -20x1,and s3 = s2 - 40x2.For product 3:
(b)Now production quantities are treated as continuous variables.Let sn be the percentage of the capacity left for the remaining products.(Note that the units of sn now are different than in part (a),so the possible values of sn now are 0 ≤ sn ≤ 100 rather than 0,1,2,3,4,5.)We now have s1 = 100,s2 = 100 -20x1,and s3 = s2 - 40x2.For product 3: 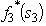 = s3 /20,with
= s3 /20,with 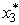 = s3 /20.For product 2:
= s3 /20.For product 2: 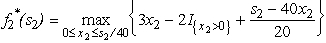 ,where
,where 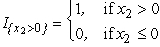 .This is linear in x2 except for the
.This is linear in x2 except for the 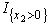 term.Therefore,we only need to examine the endpoints of the range for x2. If x2 = 0,we get
term.Therefore,we only need to examine the endpoints of the range for x2. If x2 = 0,we get 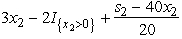 = s2 /20.If x2 = s2 /40,we get
= s2 /20.If x2 = s2 /40,we get 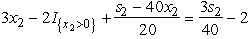 .Equating these two quantities,the breakpoint is s2 =80.So,
.Equating these two quantities,the breakpoint is s2 =80.So, 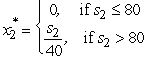 and
and 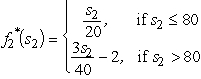 .For product 1:
.For product 1: 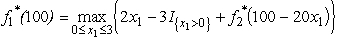 ,where
,where 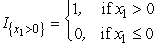 .Again,this is linear in x1 except for the
.Again,this is linear in x1 except for the 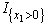 term.Therefore,we only need to examine the endpoints of the range for x1. If x1 = 0,we get
term.Therefore,we only need to examine the endpoints of the range for x1. If x1 = 0,we get 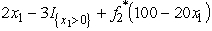 = 5.5.If x1 = 3,we get
= 5.5.If x1 = 3,we get 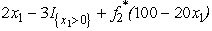 = 6 - 3 +
= 6 - 3 + 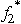 (40)= 5.So,
(40)= 5.So, 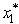 = 0 and
= 0 and 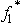 (100)= 5.5.With
(100)= 5.5.With 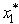 = 0,the state at stage 2 becomes s2 = 100,which leads to
= 0,the state at stage 2 becomes s2 = 100,which leads to 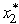 = 2.5 and s3 = 0,so
= 2.5 and s3 = 0,so 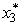 = 0.Therefore,the optimal solution is to produce 2.5 units of product 2,but none of products 1 and 3,with a profit of 5.5.This is better than with the integer restriction in part (a),as we would expect.
= 0.Therefore,the optimal solution is to produce 2.5 units of product 2,but none of products 1 and 3,with a profit of 5.5.This is better than with the integer restriction in part (a),as we would expect. 2
A company is planning its advertising strategy for next year for its three major products.Since the three products are quite different,each advertising effort will focus on a single product.In units of millions of dollars,a total of 6 is available for advertising next year,where the advertising expenditure for each product must be an integer greater than or equal to 1.The vice-president for marketing has established the objective: Determine how much to spend on each product in order to maximize total sales.The following table gives the estimated increase in sales (in appropriate units)for the different advertising expenditures. 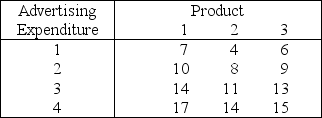 Use dynamic programming to solve this problem.
Use dynamic programming to solve this problem.
 Use dynamic programming to solve this problem.
Use dynamic programming to solve this problem.Since the decisions to be made are the advertising expenditures on the three products,the stages for a dynamic programming formulation of this problem correspond to the three products.When making the decision for a particular product,the essential information is the amount of the advertising budget still remaining,so this becomes the current state in this formulation.Let xn be the advertising dollars (in millions)spent on product n.Let sn be the amount of advertising budget remaining.Let 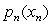 be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is
be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is 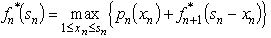 .The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3,
.The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3, 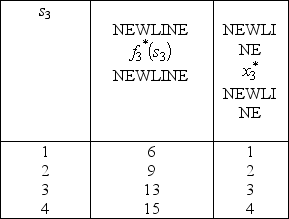 For n = 2,
For n = 2, 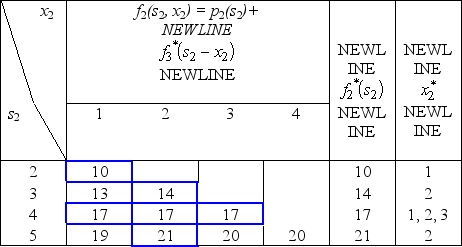 For n = 1,
For n = 1,  Hence,since s2 = 6 -
Hence,since s2 = 6 - 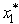 and s3 = s2 -
and s3 = s2 - 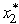 ,there are two optimal plans as given in the table below.
,there are two optimal plans as given in the table below. 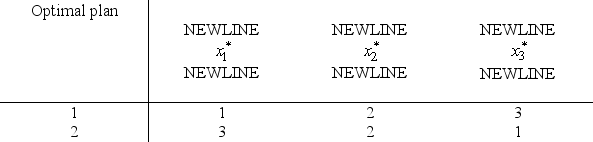
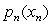 be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is
be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is 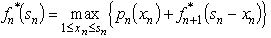 .The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3,
.The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3,  For n = 2,
For n = 2,  For n = 1,
For n = 1,  Hence,since s2 = 6 -
Hence,since s2 = 6 - 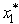 and s3 = s2 -
and s3 = s2 - 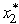 ,there are two optimal plans as given in the table below.
,there are two optimal plans as given in the table below. 
3
Consider the following integer nonlinear programming problem.Maximize Z = 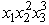 ,subject to
,subject to 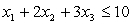
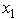 ≥ 1,
≥ 1, 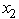 ≥ 1,
≥ 1, 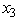 ≥ 1,and
≥ 1,and 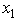 ,
, 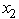 ,
, 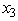 are integers.Use dynamic programming to solve this problem.
are integers.Use dynamic programming to solve this problem.
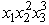 ,subject to
,subject to 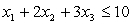
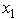 ≥ 1,
≥ 1, 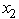 ≥ 1,
≥ 1, 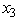 ≥ 1,and
≥ 1,and 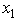 ,
, 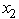 ,
, 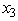 are integers.Use dynamic programming to solve this problem.
are integers.Use dynamic programming to solve this problem.The three stages involve making the decisions on the values of the three variables in order.At stage n,let the state sn be the remaining slack in the constraint 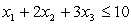 ,so s1 = 10,s2 = 10 - x1,and s3 = s2 - 2x2.Let
,so s1 = 10,s2 = 10 - x1,and s3 = s2 - 2x2.Let 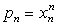 .Then
.Then 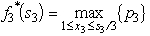 ,and
,and 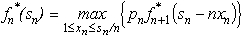 for n = 1,2.For n = 3,
for n = 1,2.For n = 3, 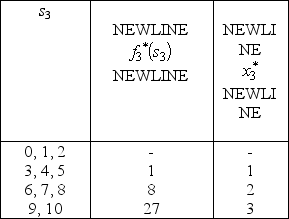 For n = 2,
For n = 2, 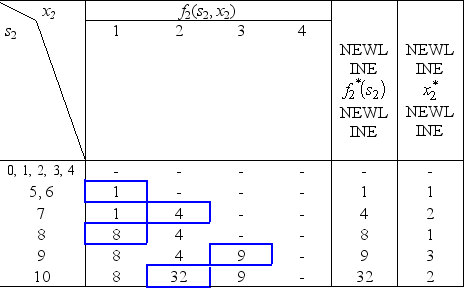 For n = 1,
For n = 1,  Since
Since 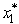 = 2 leads to s2 = 10 -
= 2 leads to s2 = 10 - 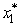 = 8 and
= 8 and 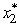 = 1,which then leads to s3 = s2 - 2
= 1,which then leads to s3 = s2 - 2 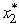 = 6 and
= 6 and 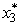 = 2,it follows that (x1,x2,x3)= (2,1,2)is optimal with Z = 16.
= 2,it follows that (x1,x2,x3)= (2,1,2)is optimal with Z = 16.
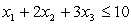 ,so s1 = 10,s2 = 10 - x1,and s3 = s2 - 2x2.Let
,so s1 = 10,s2 = 10 - x1,and s3 = s2 - 2x2.Let 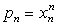 .Then
.Then 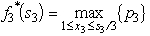 ,and
,and 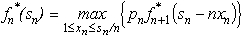 for n = 1,2.For n = 3,
for n = 1,2.For n = 3,  For n = 2,
For n = 2,  For n = 1,
For n = 1,  Since
Since 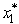 = 2 leads to s2 = 10 -
= 2 leads to s2 = 10 - 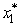 = 8 and
= 8 and 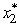 = 1,which then leads to s3 = s2 - 2
= 1,which then leads to s3 = s2 - 2 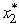 = 6 and
= 6 and 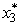 = 2,it follows that (x1,x2,x3)= (2,1,2)is optimal with Z = 16.
= 2,it follows that (x1,x2,x3)= (2,1,2)is optimal with Z = 16. 4
Consider the following nonlinear programming problem.Maximize Z = 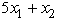 ,subject to 2
,subject to 2 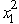 +
+ 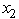 ≤ 13
≤ 13 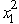 +
+ 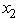 ≤ 9 and
≤ 9 and 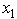 ≥ 0,
≥ 0, 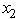 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
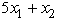 ,subject to 2
,subject to 2 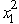 +
+ 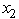 ≤ 13
≤ 13 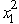 +
+ 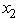 ≤ 9 and
≤ 9 and 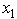 ≥ 0,
≥ 0, 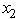 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 5 في هذه المجموعة.
فتح الحزمة
k this deck
5
Consider the following nonlinear programming problem.Maximize Z = 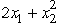 ,subject to
,subject to 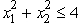 and
and 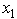 ≥ 0,
≥ 0, 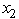 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
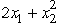 ,subject to
,subject to 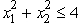 and
and 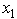 ≥ 0,
≥ 0, 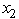 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 5 في هذه المجموعة.
فتح الحزمة
k this deck








