Deck 4: Demand Relationships Among Goods
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/18
العب
ملء الشاشة (f)
Deck 4: Demand Relationships Among Goods
1
Quasi-concavity of utility functions insures that with only two goods,these goods must be
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.
C
2
The primary additional insight provided by expanding the theory of choice from two to three goods is that a pair of goods may now be
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.
D
3
With the Cobb-Douglas utility function 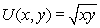 ,x and y are
,x and y are
A)net and gross substitutes.
B)net substitutes and gross complements.
C)net substitutes and neither gross substitutes or complements.
D)net and gross complements.
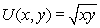 ,x and y are
,x and y areA)net and gross substitutes.
B)net substitutes and gross complements.
C)net substitutes and neither gross substitutes or complements.
D)net and gross complements.
C
4
For the Cobb-Douglas utility function with two goods,the sum of the own price elasticities of demand must be
A)0.
B)-1.
C)-2
D)any number between 0 and -.
A)0.
B)-1.
C)-2
D)any number between 0 and -.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
5
The elasticity of the compensated demand curve can be computed as
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
6
If a rise in the price x causes less y to be demanded,
A)x and y are gross complements.
B)x and y are gross substitutes.
C)x and y are net complements.
D)x and y are net substitutes.
A)x and y are gross complements.
B)x and y are gross substitutes.
C)x and y are net complements.
D)x and y are net substitutes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
7
"Hicks' Second Law of Demand" states that "most" goods must be
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.
A)gross substitutes.
B)gross complements.
C)net substitutes.
D)net complements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
8
With only two goods,x and y,if x and y are gross substitutes,a rise in px must necessarily
A)increase spending in x.
B)reduce spending in x.
C)increase spending in y.
D)reduce spending in y.
A)increase spending in x.
B)reduce spending in x.
C)increase spending in y.
D)reduce spending in y.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
9
Two goods are Hicksian (net)substitutes if a rise in the price of one causes a(n)
A)decline in the quantity demanded of the other holding nominal income constant.
B)increase in the quantity demanded of the other holding nominal income constant.
C)decline in the quantity demanded of the other holding utility constant.
D)increase in the quantity demanded of the other holding utility constant.
A)decline in the quantity demanded of the other holding nominal income constant.
B)increase in the quantity demanded of the other holding nominal income constant.
C)decline in the quantity demanded of the other holding utility constant.
D)increase in the quantity demanded of the other holding utility constant.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
10
Homogeneity of the demand function is shown by:
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
11
In the Slutsky equation for ,the income effect is given by
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
12
The attributes model of consumer choice explains the possibility that an individual does not purchase a particular good,z by assuming
A)the person's preferences do not favor z.
B)linear combinations of other goods dominate z.
C)that MUz / pz is less than the marginal utility of income.
D)z is inferior.
A)the person's preferences do not favor z.
B)linear combinations of other goods dominate z.
C)that MUz / pz is less than the marginal utility of income.
D)z is inferior.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
13
If the demand for x is given by ,which of parameter values hold?
A) .
B) .
C) .
D)None of these relations hold since the demand function is not homogeneous of degree zero in
A) .
B) .
C) .
D)None of these relations hold since the demand function is not homogeneous of degree zero in

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
14
If utility is separable in a three-good utility function  then for changes in
then for changes in 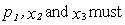
A)both be gross substitutes for x1 .
B)both be gross complements for x1 .
C)be such that if one is a gross substitute for x1 ,the other is a gross complement for x1 .
D)both be gross substitutes or both be gross complements for x.
 then for changes in
then for changes in 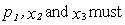
A)both be gross substitutes for x1 .
B)both be gross complements for x1 .
C)be such that if one is a gross substitute for x1 ,the other is a gross complement for x1 .
D)both be gross substitutes or both be gross complements for x.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
15
A generalization of Engel's Law is given by
A) .
B) .
C) .
D) .
A) .
B) .
C) .
D) .

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
16
Symmetry of net substitution effects is one of the principal conclusions of the theory of utility maximization.Which two mathematical theorems are used to prove this symmetry?
A)Taylor's Theorem and Fundamental Theorem of Calculus.
B)Cauchy's Theorem and DeMonre's Theorem.
C)Lagrangian Theorem and Fundamental Theorem of Calculus.
D)Envelope Theorem and Young's Theorem.
A)Taylor's Theorem and Fundamental Theorem of Calculus.
B)Cauchy's Theorem and DeMonre's Theorem.
C)Lagrangian Theorem and Fundamental Theorem of Calculus.
D)Envelope Theorem and Young's Theorem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
17
If goods x and y are complements,then the cross price elasticity of demand between them will be
A)positive.
B)negative.
C)zero.
D)infinity.
A)positive.
B)negative.
C)zero.
D)infinity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck
18
For the "Composite Commodity Theorem" to hold,all goods in the composite must
A)have constant prices.
B)have constant relative prices.
C)be used in fixed proportions.
D)be net complements.
A)have constant prices.
B)have constant relative prices.
C)be used in fixed proportions.
D)be net complements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 18 في هذه المجموعة.
فتح الحزمة
k this deck








