Deck 17: Second-Order Differential Equations
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/63
العب
ملء الشاشة (f)
Deck 17: Second-Order Differential Equations
1
A spring with a mass of 2 kg has damping constant 14, and a force of 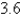 N is required to keep the spring stretched
N is required to keep the spring stretched 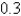 m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.
m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.
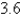 N is required to keep the spring stretched
N is required to keep the spring stretched 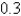 m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.
m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.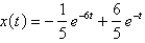
2
Solve the differential equation using the method of variation of parameters.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Use power series to solve the differential equation..
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Use power series to solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
5
A series circuit consists of a resistor , an inductor with , a capacitor with , and a -V battery. If the initial charge is 0.0008 C and the initial current is 0, find the current I(t) at time t.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
6
Use power series to solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
7
A series circuit consists of a resistor 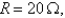 an inductor with L =
an inductor with L = 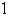 H, a capacitor with
H, a capacitor with
C =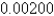 F, and a
F, and a 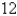 -V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
-V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
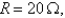 an inductor with L =
an inductor with L = 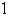 H, a capacitor with
H, a capacitor withC =
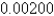 F, and a
F, and a  -V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
-V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
8
A spring has a mass of kg and its damping constant is . The spring starts from its equilibrium position with a velocity of m/s. Graph the position function for the spring constant .
A)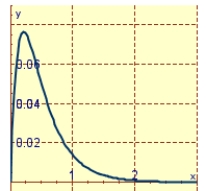
B)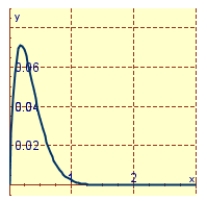
C)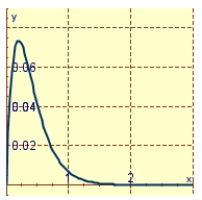
A)

B)

C)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
9
Use power series to solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
10
A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
11
Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
12
A spring with a mass of 2 kg has damping constant 14, and a force of 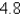 N is required to keep the spring stretched
N is required to keep the spring stretched 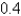 m beyond its natural length. Find the mass that would produce critical damping.
m beyond its natural length. Find the mass that would produce critical damping.
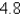 N is required to keep the spring stretched
N is required to keep the spring stretched 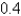 m beyond its natural length. Find the mass that would produce critical damping.
m beyond its natural length. Find the mass that would produce critical damping.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
13
A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping.
A)
B)
C)
D) 9
E)
A)
B)
C)
D) 9
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
14
Use power series to solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
15
A spring with a 3-kg mass is held stretched 0.9 m beyond its natural length by a force of 30 N. If the spring begins at its equilibrium position but a push gives it an initial velocity of m/s, find the position x(t) of the mass after t seconds.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
16
The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
17
A series circuit consists of a resistor , an inductor with , a capacitor with , and a generator producing a voltage of If the initial charge is and the initial current is 0, find the charge at time t.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
18
A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s.
A)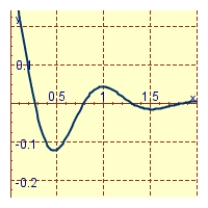
B)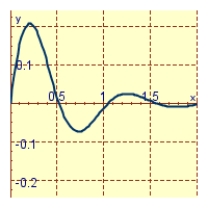
C)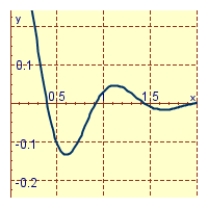
A)

B)

C)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
19
The figure shows a pendulum with length L and the angle from the vertical to the pendulum. It can be shown that , as a function of time, satisfies the nonlinear differential equation where we can use the linear approximation 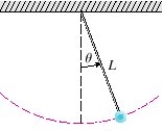
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
20
Use power series to solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
21
Solve the differential equation using the method of variation of parameters. 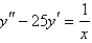
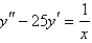

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
22
Solve the differential equation using the method of undetermined coefficients. 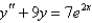
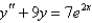

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
23
Solve the differential equation using the method of undetermined coefficients.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
24
Solve the differential equation using the method of undetermined coefficients.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
25
Solve the differential equation using the method of variation of parameters.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
26
Solve the differential equation. 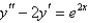
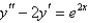

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
27
Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
28
Solve the initial-value problem using the method of undetermined coefficients. 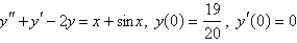
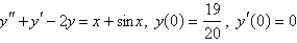

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
29
Solve the differential equation using the method of variation of parameters. 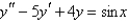
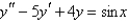

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
30
Solve the differential equation using the method of undetermined coefficients.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
31
Graph the particular solution and several other solutions.
A)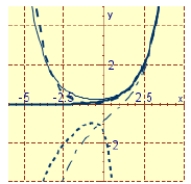
B)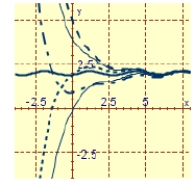
C)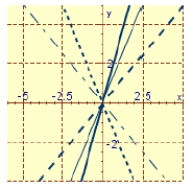
A)

B)

C)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
32
Solve the differential equation using the method of variation of parameters. 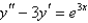
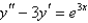

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
33
Solve the differential equation using the method of variation of parameters.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
34
Solve the differential equation. 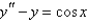
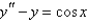

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
35
Solve the initial-value problem using the method of undetermined coefficients. 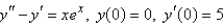
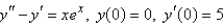

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
36
Solve the differential equation using the method of variation of parameters. 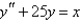
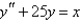

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
38
Solve the differential equation using the method of undetermined coefficients. 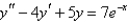
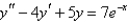

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
39
Solve the differential equation using the method of variation of parameters.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
40
Solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
41
Solve the differential equation. 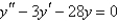
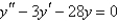

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
42
Solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
43
Solve the boundary-value problem, if possible. 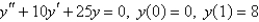
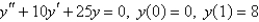

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
44
Solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
45
Solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
46
Solve the boundary-value problem, if possible.
A)
B)
C)
D)
E) No solution
A)
B)
C)
D)
E) No solution

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
47
Solve the initial-value problem. 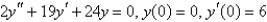
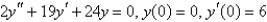

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
48
Solve the differential equation. 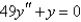
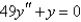

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
49
Solve the differential equation. 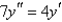
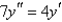

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
50
Solve the differential equation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
51
Solve the differential equation.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
52
Solve the initial-value problem. .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
53
Solve the initial-value problem. 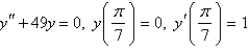
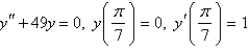

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
54
Find f by solving the initial value problem. ; ,
A) + 4 x - 10
B) + 2 x
C) + 2 x
D) + 4 x - 5
A) + 4 x - 10
B) + 2 x
C) + 2 x
D) + 4 x - 5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
55
Solve the boundary-value problem, if possible.
A)
B)
C)
D)
E) No solution
A)
B)
C)
D)
E) No solution

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
56
Solve the initial-value problem.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
57
Solve the initial-value problem.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
58
Solve the initial value problem. 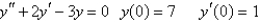
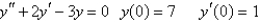

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
59
Solve the initial-value problem.
A)
B)
C)
D)
E) None of these
A)
B)
C)
D)
E) None of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
60
Solve the differential equation. 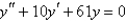
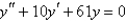

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
61
Solve the boundary-value problem, if possible. 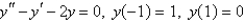
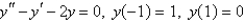

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
62
Solve the initial-value problem. 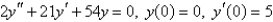
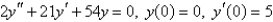

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck
63
Solve the differential equation. 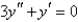
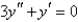

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 63 في هذه المجموعة.
فتح الحزمة
k this deck








