Deck 14: Partial Derivatives
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/132
العب
ملء الشاشة (f)
Deck 14: Partial Derivatives
1
Find three positive numbers whose sum is and whose product is a maximum.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Find the direction in which the maximum rate of change of f at the given point occurs.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Use Lagrange multipliers to find the maximum value of the function subject to the given constraint.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
4
Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is
A) , ,
B) 4, 8, 16
C) , ,
D) 32, , 16
E) 32, 32, 32
A) , ,
B) 4, 8, 16
C) , ,
D) 32, , 16
E) 32, 32, 32

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
5
Use Lagrange multipliers to find the maximum value of the function subject to the given constraints. 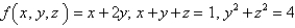
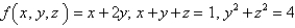

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find the points on the surface that are closest to the origin.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
7
Suppose (1, 1) is a critical point of a function f with continuous second derivatives. In the case of , , what can you say about f ?
A) f has a local maximum at (1,1)
B) f has a saddle point at (1,1)
C) f has a local minimum at (1,1)
A) f has a local maximum at (1,1)
B) f has a saddle point at (1,1)
C) f has a local minimum at (1,1)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
8
Find and classify the relative extrema and saddle points of the function for and .
A) None
B) Relative maximum
C) Saddle point
D) Relative minimum
A) None
B) Relative maximum
C) Saddle point
D) Relative minimum

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
9
Use Lagrange multipliers to find the maximum and minimum values of the function 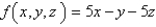 subject to the constraints
subject to the constraints 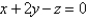 and
and 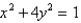 .
.
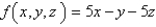 subject to the constraints
subject to the constraints 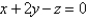 and
and 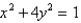 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
10
Find all the saddle points of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
11
Find the dimensions of the rectangular box with largest volume if the total surface area is given as .
A) cm, 1.75 cm, 1.75 cm
B) cm, cm, 1.75 cm
C) cm, cm, cm
D) cm, cm, cm
E) cm, cm, 3.5 cm
A) cm, 1.75 cm, 1.75 cm
B) cm, cm, 1.75 cm
C) cm, cm, cm
D) cm, cm, cm
E) cm, cm, 3.5 cm

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
12
Use Lagrange multipliers to find the maximum value of the function subject to the given constraint.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
13
Use Lagrange multipliers to find the maximum and the minimum of f subject to the given constraint(s). 


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
14
At what point is the following function a local minimum?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
15
Use Lagrange multipliers to find the minimum value of the function subject to the given constraints. 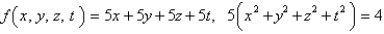
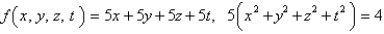

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
16
Find the critical points of the function.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find the shortest distance from the point to the plane .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
18
At what point is the following function a local maximum?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
19
Find the absolute extrema of the function on the closed triangular region with vertices , and .
A) Absolute minimum 0, Absolute maximum 5
B) Absolute minimum -5, Absolute maximum 5
C) Absolute minimum -5, Absolute maximum 17
D) Absolute minimum 5, Absolute maximum 17
A) Absolute minimum 0, Absolute maximum 5
B) Absolute minimum -5, Absolute maximum 5
C) Absolute minimum -5, Absolute maximum 17
D) Absolute minimum 5, Absolute maximum 17

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find the absolute minimum value of the function on the set D. D is the region bounded by the parabola and the line
A)
B)
C)
D) 30
E) 0
A)
B)
C)
D) 30
E) 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
21
Find the equation of the tangent plane to the given surface at the specified point. 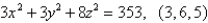
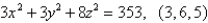

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
22
Find the directional derivative of the function at the point in the direction of the unit vector that makes the angle with the positive x-axis.
A)
B) 1
C)
D) 11
A)
B) 1
C)
D) 11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
23
Find the directional derivative of at the point (1, 3) in the direction toward the point (3, 1). Select the correct answer.
A)
B)
C)
D) 28
E) none of these
A)
B)
C)
D) 28
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
24
Find three positive numbers whose sum is 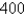 and whose product is a maximum.
and whose product is a maximum.
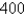 and whose product is a maximum.
and whose product is a maximum.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
25
Suppose that over a certain region of space the electrical potential V is given by . Find the rate of change of the potential at in the direction of the vector .
A)
B) 44
C) -2.91
D) 20
E)
A)
B) 44
C) -2.91
D) 20
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
26
Find the equation of the normal line to the given surface at the specified point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
27
Find and classify the relative extrema and saddle points of the function 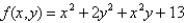 .
.
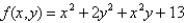 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
28
Which of the given points are the points on the hyperboloid where the normal line is parallel to the line that joins the points and .
Select all that apply.
A)
B)
C)
D)
E)
Select all that apply.
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
29
Find the maximum rate of change of at the point (2,1). In what direction does it occur?
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the maximum rate of change of f at the given point. 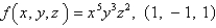
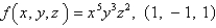

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
31
Find equations for the tangent plane and the normal line to the surface with equation at the point
A) ,
B) ,
C) ,
D) ,
A) ,
B) ,
C) ,
D) ,

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
32
Find the gradient of the function .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
33
A cardboard box without a lid is to have a volume of 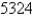 cm
cm 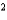 . Find the dimensions that minimize the amount of cardboard used.
. Find the dimensions that minimize the amount of cardboard used.
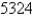 cm
cm 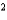 . Find the dimensions that minimize the amount of cardboard used.
. Find the dimensions that minimize the amount of cardboard used.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
34
Evaluate the gradient of f at the point P. 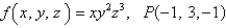
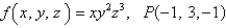

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find equations for the tangent plane and the normal line to the surface with equation at the point
A) ,
B) ,
C) ,
D) ,
A) ,
B) ,
C) ,
D) ,

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
36
Find the absolute extrema of the function 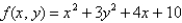 on the region bounded by the disk defined by
on the region bounded by the disk defined by 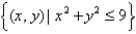 .
.
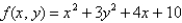 on the region bounded by the disk defined by
on the region bounded by the disk defined by 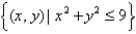 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
37
Find three positive real numbers whose sum is 388 and whose product is as large as possible.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
38
Find the direction in which the function 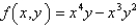 decreases fastest at the point
decreases fastest at the point 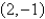 .
.
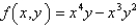 decreases fastest at the point
decreases fastest at the point 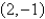 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
39
Find the local maximum, and minimum value and saddle points of the function. 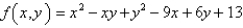
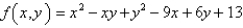

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
40
If use the gradient vector to find the tangent line to the level curve at the point .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
41
Use the Chain Rule to find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find the limit if 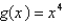 .
. 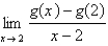
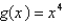 .
. 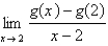

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
43
The radius of a right circular cone is increasing at a rate of 5 in/s while its height is decreasing at a rate of 3.6 in/s. At what rate is the volume of the cone changing when the radius is in. and the height is in.?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
44
Find the differential of the function
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
45
Use the Chain Rule to find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
46
Use the Chain Rule to find 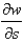 where
where 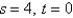 .
. 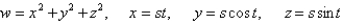
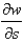 where
where 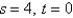 .
. 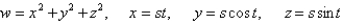

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find an equation of the tangent plane to the given surface at the specified point. 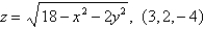

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
48
Use the Chain Rule to find and if and
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find the equation of the tangent plane to the given surface at the specified point. 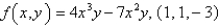

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
50
Use the equation to find .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
51
The length l, width w and height h of a box change with time. At a certain instant the dimensions are 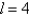 and
and 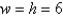 , and l and w are increasing at a rate of 10 m/s while h is decreasing at a rate of 1 m/s. At that instant find the rates at which the surface area is changing.
, and l and w are increasing at a rate of 10 m/s while h is decreasing at a rate of 1 m/s. At that instant find the rates at which the surface area is changing.
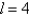 and
and 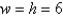 , and l and w are increasing at a rate of 10 m/s while h is decreasing at a rate of 1 m/s. At that instant find the rates at which the surface area is changing.
, and l and w are increasing at a rate of 10 m/s while h is decreasing at a rate of 1 m/s. At that instant find the rates at which the surface area is changing.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
52
Use implicit differentiation to find 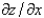 .
. 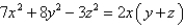
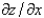 .
. 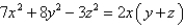

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
53
Find the equation of the tangent plane to the given surface at the specified point.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
54
Use the Chain Rule to find
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
55
Find the gradient of the function 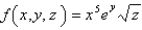 .
.
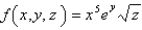 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the equation of the normal line to the given surface at the specified point. 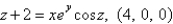
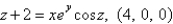

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
57
A boundary stripe 2 in. wide is painted around a rectangle whose dimensions are 100 ft by 240 ft. Use differentials to approximate the number of square feet of paint in the stripe.
A) 113
B) 113.81
C) 113.23
D) 113.89
E) 113.33
A) 113
B) 113.81
C) 113.23
D) 113.89
E) 113.33

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
58
Use partial derivatives to find the implicit partial derivatives 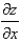 and
and 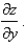
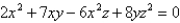
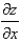 and
and 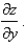
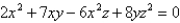

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find the gradient of 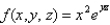 at the point
at the point 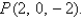
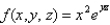 at the point
at the point 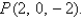

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
60
Use differentials to estimate the amount of metal in a closed cylindrical can that is 12 cm high and 8 cm in diameter if the metal in the top and bottom is 0.09 cm thick and the metal in the sides is 0.01 cm thick. (rounded to the nearest hundredth.)
A) 8.34
B) 6.99
C) 6.91
D) 6.7
E)
A) 8.34
B) 6.99
C) 6.91
D) 6.7
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find for the function .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
62
If 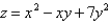 and
and 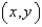 changes from (2, 1) to
changes from (2, 1) to 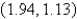 find dz.
find dz.
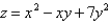 and
and 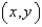 changes from (2, 1) to
changes from (2, 1) to 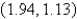 find dz.
find dz.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
63
Find the differential of the function. 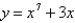
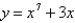

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
64
Use the linearization L(x, y) of the function. 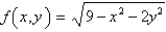 at
at 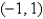 to approximate
to approximate 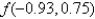 .
.
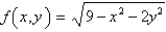 at
at 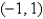 to approximate
to approximate 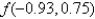 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
65
How many nth-order partial derivatives does a function of two variables have?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find the differential of the function 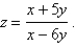
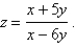

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
67
Find for the function
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
68
Find the indicated partial derivative.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
69
Use implicit differentiation to find
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
70
Use differentials to estimate the amount of tin in a closed tin can with diameter 8 cm and height 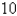 cm if the tin is 0.04 cm thick.
cm if the tin is 0.04 cm thick.
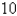 cm if the tin is 0.04 cm thick.
cm if the tin is 0.04 cm thick.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find the indicated partial derivative.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find the differential of the function 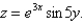
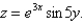

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
73
Let 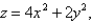 and suppose that
and suppose that 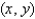 changes from
changes from 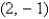 to
to 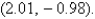 (a) Compute
(a) Compute 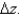 (b) Compute
(b) Compute 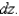
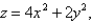 and suppose that
and suppose that 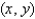 changes from
changes from 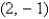 to
to 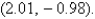 (a) Compute
(a) Compute 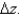 (b) Compute
(b) Compute 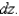

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
74
The height of a hill (in feet) is given by where x is the distance (in miles) east and y is the distance (in miles) north of your cabin. If you are at a point on the hill 1 mile north and 1 mile east of your cabin, what is the rate of change of the height of the hill (a) in a northerly direction and (b) in an easterly direction?
A) (a) 570 ft/mi, (b) 690 ft/mi
B) (a) -570 ft/mi, (b) 690 ft/mi
C) (a) 690 ft/mi, (b) 570 ft/mi
D) (a) 690 ft/mi, (b) -570 ft/mi
A) (a) 570 ft/mi, (b) 690 ft/mi
B) (a) -570 ft/mi, (b) 690 ft/mi
C) (a) 690 ft/mi, (b) 570 ft/mi
D) (a) 690 ft/mi, (b) -570 ft/mi

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
75
Find for the function
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
76
Use the definition of partial derivatives as limits to find if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
77
The wind-chill index I is the perceived temperature when the actual temperature is T and the wind speed is v so we can write 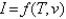 . The following table of values is an excerpt from a table compiled by the National Atmospheric and Oceanic Administration. Use the table to find a linear approximation
. The following table of values is an excerpt from a table compiled by the National Atmospheric and Oceanic Administration. Use the table to find a linear approximation 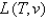 to the wind chill index function when T is near
to the wind chill index function when T is near 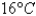 and v is near 30 kmh.
and v is near 30 kmh.
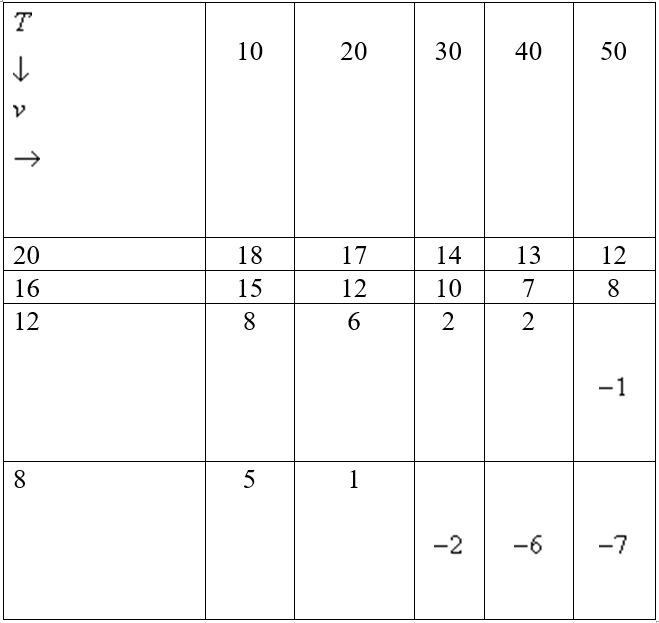
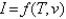 . The following table of values is an excerpt from a table compiled by the National Atmospheric and Oceanic Administration. Use the table to find a linear approximation
. The following table of values is an excerpt from a table compiled by the National Atmospheric and Oceanic Administration. Use the table to find a linear approximation 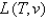 to the wind chill index function when T is near
to the wind chill index function when T is near 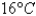 and v is near 30 kmh.
and v is near 30 kmh.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
78
Find the linearization L(x, y) of the function at the given point. 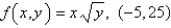 Round the answers to the nearest hundredth.
Round the answers to the nearest hundredth.
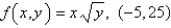 Round the answers to the nearest hundredth.
Round the answers to the nearest hundredth.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
79
Use implicit differentiation to find
A)
B)
C)
D)
A)
B)
C)
D)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck
80
Find for .
A)
B)
C)
D)
E) 0
A)
B)
C)
D)
E) 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 132 في هذه المجموعة.
فتح الحزمة
k this deck








