Deck 9: Vectors and the Geometry of Space
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/269
العب
ملء الشاشة (f)
Deck 9: Vectors and the Geometry of Space
1
Describe the surface whose equation in cylindrical coordinates is r = 3.
A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis
A
2
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
Paraboloid
3
If 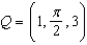 in cylindrical coordinates, find rectangular coordinates of Q.
in cylindrical coordinates, find rectangular coordinates of Q.
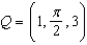 in cylindrical coordinates, find rectangular coordinates of Q.
in cylindrical coordinates, find rectangular coordinates of Q.(0, 1, 3)
4
Convert from spherical coordinates to rectangular coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
5
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
6
Convert from rectangular coordinates to spherical coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
7
Convert from cylindrical coordinates to rectangular coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
8
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
9
Convert from spherical coordinates to rectangular coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
10
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
11
Convert from rectangular coordinates to spherical coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
12
Convert from rectangular coordinates to cylindrical coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
13
Convert from cylindrical coordinates to rectangular coordinates.
A)
B)
C)
D)
E)
F) .
G) .
H)
A)
B)
C)
D)
E)
F) .
G) .
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
14
Convert from rectangular coordinates to cylindrical coordinates.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
15
If 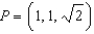 in rectangular coordinates, find the spherical coordinates of P.
in rectangular coordinates, find the spherical coordinates of P.
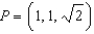 in rectangular coordinates, find the spherical coordinates of P.
in rectangular coordinates, find the spherical coordinates of P.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
16
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
17
Describe the surface whose equation in cylindrical coordinates is  = 3.
= 3.
A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis
 = 3.
= 3.A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
18
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Positive z-axis
E)Negative z-axis
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Positive z-axis
E)Negative z-axis
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
19
Describe the surface whose equation in cylindrical coordinates is z = 3.
A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
E)Horizontal plane or half-plane
B)Cylinder with horizontal axis
F)Paraboloid
C)Sphere
G)Cone or half-cone with vertical axis
D)Vertical plane or half-plane
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
20
Describe the surface whose equation in cylindrical coordinates is .
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis
A)Cylinder with vertical axis
B)Cylinder with horizontal axis
C)Sphere
D)Vertical plane or half-plane
E)Horizontal plane or half-plane
F)Paraboloid
G)Cone or half-cone with vertical axis
H)Cone or half-cone with horizontal axis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
21
Convert the point (0, -5, 0) to cylindrical and spherical coordinates.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
22
Find the set of intersection of the surfaces whose equations in spherical coordinates are 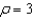 and
and 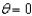 .
.
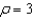 and
and 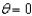 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
23
Find cylindrical and spherical equations for the surface whose equation in rectangular coordinates is x = 2. Describe the surface.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
24
Find the set of intersection of the surfaces whose equations in spherical coordinates are 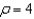 and
and 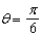 .
.
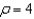 and
and 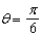 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
25
Describe the surface whose equation in cylindrical coordinates is 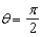 .
.
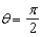 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
26
Describe the surface whose equation in spherical coordinates is 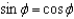 .
.
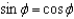 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
27
Let A, B, and C be three points on the unit sphere centered at the origin whose spherical coordinates are A = (1, 0, 0), B = 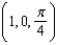 , and C =
, and C = 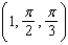 .(a) Find the angle between
.(a) Find the angle between 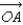 and
and 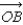 .(b) Find the angle between
.(b) Find the angle between 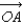 and
and 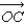 .(c) Find the angle between
.(c) Find the angle between 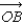 and
and 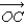 .
.
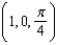 , and C =
, and C = 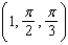 .(a) Find the angle between
.(a) Find the angle between 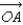 and
and 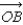 .(b) Find the angle between
.(b) Find the angle between 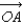 and
and 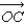 .(c) Find the angle between
.(c) Find the angle between 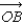 and
and 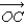 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
28
Describe the surface whose equation in cylindrical coordinates is 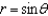 .
.
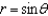 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
29
Find rectangular and spherical equations for the surface whose equation in cylindrical coordinates is 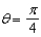 . Describe the surface.
. Describe the surface.
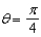 . Describe the surface.
. Describe the surface.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
30
Find the set of intersection of the surfaces whose equations in spherical coordinates are 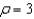 and
and 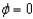 .
.
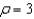 and
and 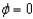 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
31
Sketch the solid given in cylindrical coordinates by 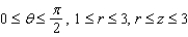 .
. 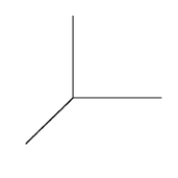
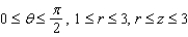 .
. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
32
Sketch the solid given in spherical coordinates by 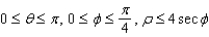 .
. 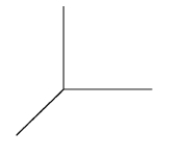
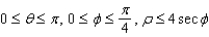 .
. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
33
Find the set of intersection of the surfaces whose equations in spherical coordinates are 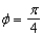 and
and 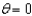 .
.
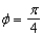 and
and 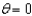 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
34
Find rectangular and cylindrical equations for the surface whose equation in spherical coordinates is 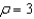 . Describe the surface.
. Describe the surface.
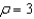 . Describe the surface.
. Describe the surface.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
35
Find the set of intersection of the surfaces whose equations in spherical coordinates are 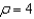 and
and 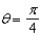 .
.
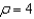 and
and 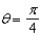 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
36
New Orleans is situated at latitude 30° N and longitude 90° W, and New York is situated at latitude 41° N and longitude 74° W. Find the distance from New Orleans to New York, assuming that the radius of the earth is 3960 miles.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
37
Describe in words or sketch the solid represented in cylindrical coordinates by the inequalities 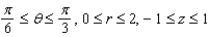 .
. 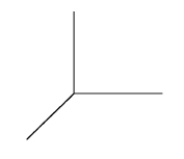
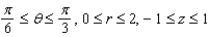 .
. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
38
Use the given data:
Los Angeles: Latitude 34.05°N and Longitude 118.25°W;
Hawaii: Latitude 21.3°N and Longitude 157.83°W.Find the distance from Los Angeles to Hawaii (Assume the radius of earth is 3960 miles.)
Los Angeles: Latitude 34.05°N and Longitude 118.25°W;
Hawaii: Latitude 21.3°N and Longitude 157.83°W.Find the distance from Los Angeles to Hawaii (Assume the radius of earth is 3960 miles.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
39
Convert the point 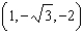 to cylindrical and spherical coordinates.
to cylindrical and spherical coordinates.
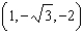 to cylindrical and spherical coordinates.
to cylindrical and spherical coordinates.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
40
Describe in words the solid represented in spherical coordinates by the inequality 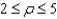 .
.
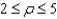 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
41
Identify the trace of the surface in the plane z = 1.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
42
Identify the trace of the surface in the plane z = 0.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
43
Identify the trace of the surface in the plane x = y.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
44
Given points A = 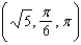 and B =
and B = 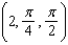 in spherical coordinates, find the distance between the two points.
in spherical coordinates, find the distance between the two points.
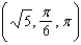 and B =
and B = 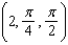 in spherical coordinates, find the distance between the two points.
in spherical coordinates, find the distance between the two points.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
45
Given points A = 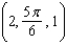 and B =
and B = 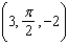 in cylindrical coordinates, find the distance between the two points.
in cylindrical coordinates, find the distance between the two points.
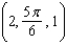 and B =
and B = 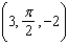 in cylindrical coordinates, find the distance between the two points.
in cylindrical coordinates, find the distance between the two points.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
46
Identify the trace of the surface in the plane x = 1.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
47
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)hyperbolic paraboloid
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)hyperbolic paraboloid

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
48
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
49
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
50
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
51
Identify the trace of the surface in the plane z = 1.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
52
Identify the trace of the surface in the plane x = 0.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
53
Identify the trace of the surface in the plane x = 0.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
54
Identify the trace of the surface in the plane y = 1.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
55
Identify the trace of the surface in the plane x = 1.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
56
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
57
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
58
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
59
Identify the surface .
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)
A)ellipsoid but not a sphere
B)hyperboloid of one sheet
C)hyperboloid of two sheets
D)cylinder
E)sphere
F)elliptic but not circular paraboloid
G)cone
H)circular paraboloid (figure of revolution)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
60
Identify the trace of the surface in the plane y = 0.
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line
A)ellipse but not a circle
B)parabola
C)hyperbola
D)circle
E)two parallel straight lines
F)two intersecting straight lines
G)point
H)straight line

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
61
Let f(x, y) = . If x = 1, find f(x, 2x).
A)1
B)2
C)3
D)4
E)8
F)9
G)16
H)27
A)1
B)2
C)3
D)4
E)8
F)9
G)16
H)27

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
62
Sketch and identify the quadric surface given by 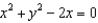 .
. 
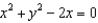 .
. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
63
Find the range of the function f(x, y) = .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
64
Find the domain of the function f(x, y) = .
A)All points on or to the left of
B)All points on or to the right of
C)All points to the left of
D)All points to the right of
E)All points on or to the left of x = 0
F)All points on or to the right of x = 0
G)All points to the left of x = 0
H)All points in the xy-plane
A)All points on or to the left of
B)All points on or to the right of
C)All points to the left of
D)All points to the right of
E)All points on or to the left of x = 0
F)All points on or to the right of x = 0
G)All points to the left of x = 0
H)All points in the xy-plane

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
65
Describe the trace of the surface z = 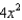 = 0 in the plane z = 1.
= 0 in the plane z = 1.
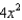 = 0 in the plane z = 1.
= 0 in the plane z = 1.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find the coordinates of the point(s) of intersection of the line x = 1 - t, y = 1 - t, z = 4t and the surface z = 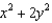 .
.
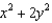 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
67
Let f(x, y) = . If x = 2, find f(x, 2x).
A)12
B)16
C)24
D)28
E)32
F)36
G)42
H)48
A)12
B)16
C)24
D)28
E)32
F)36
G)42
H)48

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
68
Let S be the quadric surface given by 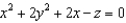 . What kind of surface is S?
. What kind of surface is S?
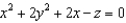 . What kind of surface is S?
. What kind of surface is S?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
69
Let f(x, y) = x sin y. If x = , find f(x, x/2).
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
70
Find the domain of the function f(x, y) = .
A)All points on or to the left of e.All points on or to the left of x = 0
B)All points on or to the right of f.All points on or to the right of x = 0
C)All points to the left of g.All points to the left of x = 0
D)All points to the right of h.All points in the xy-plane
A)All points on or to the left of e.All points on or to the left of x = 0
B)All points on or to the right of f.All points on or to the right of x = 0
C)All points to the left of g.All points to the left of x = 0
D)All points to the right of h.All points in the xy-plane

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find the range of the function f(x, y) = .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
72
Find the range of the function f(x, y) = .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
73
Let S be the quadric surface given by 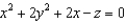 . What are the traces of S in each of the three coordinate planes?
. What are the traces of S in each of the three coordinate planes?
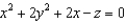 . What are the traces of S in each of the three coordinate planes?
. What are the traces of S in each of the three coordinate planes?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
74
Which of the following is not a quadric surface?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
75
Let f(x, y) = x sin y. Find f .
A)
B)
C)
D)
E)
F)
G)1
H)0
A)
B)
C)
D)
E)
F)
G)1
H)0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
76
Identify the graph of the function f(x, y) = .
A)Cone
B)Paraboloid
C)Ellipsoid
D)Hyperboloid of one sheet
E)Hyperboloid of two sheets
F)Hyperbolic cylinder
G)Elliptic cylinder
H)Parabolic cylinder
A)Cone
B)Paraboloid
C)Ellipsoid
D)Hyperboloid of one sheet
E)Hyperboloid of two sheets
F)Hyperbolic cylinder
G)Elliptic cylinder
H)Parabolic cylinder

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
77
Sketch the graph of 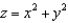 in
in 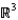 , and name the surface.
, and name the surface. 
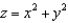 in
in 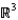 , and name the surface.
, and name the surface. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
78
Find the domain of the function f(x, y) = .
A)All points on or to the left of e.All points on or to the left of x = 0
B)All points on or to the right of f.All points on or to the right of x = 0
C)All points to the left of g.All points to the left of x = 0
D)All points to the right of h.All points in the xy-plane
A)All points on or to the left of e.All points on or to the left of x = 0
B)All points on or to the right of f.All points on or to the right of x = 0
C)All points to the left of g.All points to the left of x = 0
D)All points to the right of h.All points in the xy-plane

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
79
Sketch the graph of 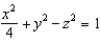 in
in 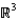 , and name the surface.
, and name the surface. 
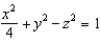 in
in 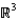 , and name the surface.
, and name the surface. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck
80
Describe the vertical traces x = 0 and the horizontal traces z = -1 (if any) for the surfaces 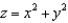 and
and 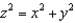 .
.
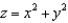 and
and 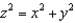 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 269 في هذه المجموعة.
فتح الحزمة
k this deck








