Deck 10: Vector Functions
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/111
العب
ملء الشاشة (f)
Deck 10: Vector Functions
1
Find a parametric representation for the surface consisting of that part of the cylinder 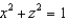 that lies between the planes
that lies between the planes  and y = 3.
and y = 3.
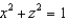 that lies between the planes
that lies between the planes  and y = 3.
and y = 3.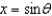 ,
, 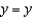 ,
, 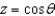 ,
, 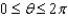 ,
, 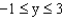
2
Are the two planes parallel? Justify your answer.
True
3
Find a parametric representation for the surface
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
F) , ,
G) , ,
H) , ,
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
F) , ,
G) , ,
H) , ,
, ,
4
A picture of a circular cylinder with radius a and height h is given below. Find a parametric representation of the cylinder. 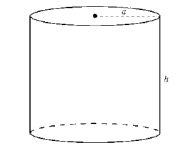


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
5
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
6
Find a parametric representation for the surface consisting of that part of the hyperboloid 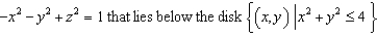 .
.
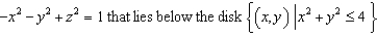 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
7
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
8
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
9
Find a parametric representation for the surface consisting of that part of the hyperboloid 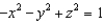 that lies below the rectangle
that lies below the rectangle 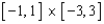 .
.
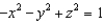 that lies below the rectangle
that lies below the rectangle 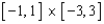 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
10
Identify the surface with the vector equation 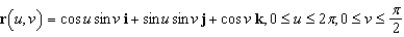 . (Hint: First consider
. (Hint: First consider 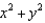 .)
.)
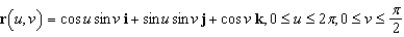 . (Hint: First consider
. (Hint: First consider 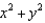 .)
.)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
11
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
12
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
13
Find a parametric representation for the surface consisting of that part of the elliptic paraboloid 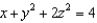 that lies in front of the plane x = 0.
that lies in front of the plane x = 0.
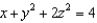 that lies in front of the plane x = 0.
that lies in front of the plane x = 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
14
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
15
Let the position function of a particle be . Find the velocity of the particle when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
16
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
17
Find a parametric representation for the surface consisting of the upper half of the ellipsoid .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
18
Identify the surface with the vector equation 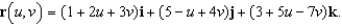
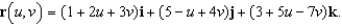

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
19
Identify the geometric object that is represented by parametric equations .
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere
A)A plane
B)A cone
C)A straight line
D)A circular cylinder
E)A circle
F)A circular disk
G)A helix
H)A sphere

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
20
Find a parametric representation for the surface consisting of that part of the plane z = x + 3 that lies inside the cylinder 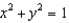 .
.
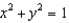 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
21
Let the position function of a particle be . Find the tangential component of the acceleration vector when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
22
Let the velocity of a particle be , and let its position when t = 0 be . Find its position when t = 2.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
23
Suppose a particle moves in the plane according to the vector-valued function 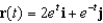 , where t represents time. Find
, where t represents time. Find 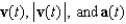 , and sketch a graph showing the path taken by the particle indicating the direction of motion.
, and sketch a graph showing the path taken by the particle indicating the direction of motion. 
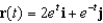 , where t represents time. Find
, where t represents time. Find 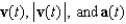 , and sketch a graph showing the path taken by the particle indicating the direction of motion.
, and sketch a graph showing the path taken by the particle indicating the direction of motion. 

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
24
For 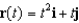 , find
, find 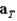 and
and 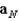 , the tangential and normal components of acceleration.
, the tangential and normal components of acceleration.
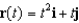 , find
, find 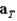 and
and 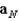 , the tangential and normal components of acceleration.
, the tangential and normal components of acceleration.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
25
Let the position function of a particle be . Find the acceleration of the particle when t = 0.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
26
A particle is traveling along a helix whose vector equation is given by 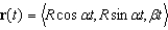 . Show that its velocity and acceleration are orthogonal at all times.
. Show that its velocity and acceleration are orthogonal at all times.
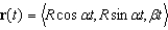 . Show that its velocity and acceleration are orthogonal at all times.
. Show that its velocity and acceleration are orthogonal at all times.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
27
A paper carrier is traveling 60 miles per hour down a straight road in the direction of the vector i when he throws a paper out the car window with a velocity (relative to the car) in the direction of j and of magnitude 10 miles per hour.(a) Find the velocity of the paper relative to the ground when the paper carrier releases it.(b) Find the speed of the paper at that time.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
28
Let a (t), v (t), and r (t) denote the acceleration, velocity, and position at time t of an object moving in the xy-plane. Find r (t), given that 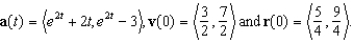
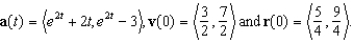

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
29
Let the position function of a particle be . Find the speed of the particle when .
A)1
B)4
C)3
D)
E)
F)
G)
H)
A)1
B)4
C)3
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
30
A person is standing 80 feet from a tall cliff. She throws a rock at 80 feet per second at an angle of 45° from the horizontal. Neglecting air resistance and discounting the height of the person, how far up the cliff does it hit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
31
Is it possible for the velocity of a particle to be zero at the same time its acceleration is not zero? Explain.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
32
Let the position function of a particle be . Find the smallest value of its speed.
A)0
B)1
C)
D)
E)2
F)
G)
H)
A)0
B)1
C)
D)
E)2
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
33
Let the acceleration of a particle be , and let its velocity when t = 0 be . Find its speed when t = 2.
A)
B)
C)
D)
E)3
F)
G)
H)
A)
B)
C)
D)
E)3
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
34
Let the acceleration of a particle be , and let its velocity when t = 0 be . Find its velocity when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
35
Suppose a particle is moving in the xy-plane so that its position vector at time t is given by 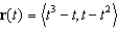 . Find the velocity, speed, and acceleration of the particle at time t = 2.
. Find the velocity, speed, and acceleration of the particle at time t = 2.
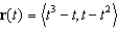 . Find the velocity, speed, and acceleration of the particle at time t = 2.
. Find the velocity, speed, and acceleration of the particle at time t = 2.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
36
If a particle moves in a plane with constant acceleration, show that its path is a straight line or a parabola.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
37
Floyd Thunderfoot is a punter for the Vikings. Today the Vikings are playing the Bears in the Metrodome. The Bears stop the Vikings at the Vikings' 40 yard line (line of scrimmage), and Floyd is called in to punt. Floyd needs to kick from 10 yards behind the line of scrimmage in order to get the punt off in time. If the ball has a hang time of 4 seconds and lands at the Bears' 10 yard line, at what angle did Floyd kick the ball, and at what speed? (Ignore air resistance.)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
38
Let the position function of a particle be r (t) = sin 3t i+cos 3t j+sin 4t k. Find the smallest value of its speed.
A)1
B)2
C)9
D)
E)0
F)
G)
H)3
A)1
B)2
C)9
D)
E)0
F)
G)
H)3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
39
Let the position function of a particle be . Find the normal component of the acceleration vector when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
40
A cannon sits on top of a vertical tower 264 feet tall. It fires a cannonball at 80 ft/s. If the barrel of the cannon is elevated 30 degrees from the horizontal, find how far from the base of the tower the cannonball will land (assuming the ground around the tower is level).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
41
A helix has radius 5 and height 6, and makes 4 revolutions. Find parametric equations of this helix. What is the arc length of the helix?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
42
Find the unit normal vector N(t) to the curve r (t) = when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
43
Find the arc length of the curve given by 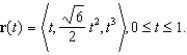
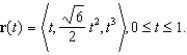

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
44
Find the arc length of the curve given by 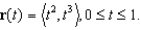
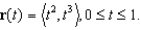

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
45
Find the length of the curve
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
46
Find the curvature of the curve
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
47
Find the length of the curve
A)
B)6
C)8
D)10
E)189
F)14
G)16
H)18
A)
B)6
C)8
D)10
E)189
F)14
G)16
H)18

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
48
Find the length of the circular helix described by 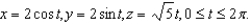
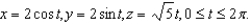

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
49
Find the length of the curve
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
50
Find the unit normal vector N(t) to the curve r (t) = when t = 0.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
51
Find the unit tangent vector T(t) to the curve r (t) = when t = 0.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
52
If 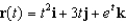 , find the acceleration vector and the tangential component of the acceleration vector.
, find the acceleration vector and the tangential component of the acceleration vector.
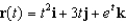 , find the acceleration vector and the tangential component of the acceleration vector.
, find the acceleration vector and the tangential component of the acceleration vector.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
53
Let 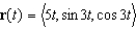 . Show that the velocity vector is perpendicular to the acceleration vector.
. Show that the velocity vector is perpendicular to the acceleration vector.
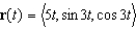 . Show that the velocity vector is perpendicular to the acceleration vector.
. Show that the velocity vector is perpendicular to the acceleration vector.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
54
A particle is moving along the curve described by the parametric equations 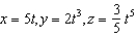 . Determine the velocity and acceleration vectors as well as the speed of the particle when t = 3.
. Determine the velocity and acceleration vectors as well as the speed of the particle when t = 3.
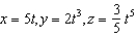 . Determine the velocity and acceleration vectors as well as the speed of the particle when t = 3.
. Determine the velocity and acceleration vectors as well as the speed of the particle when t = 3.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
55
Let 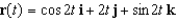 . Show that the acceleration vector is parallel to the normal vector N(t).
. Show that the acceleration vector is parallel to the normal vector N(t).
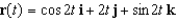 . Show that the acceleration vector is parallel to the normal vector N(t).
. Show that the acceleration vector is parallel to the normal vector N(t).
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
56
Find the curvature of the curve at t = 0.
A)0
B)
C)
D)
E)1
F)2
G)4
H)8
A)0
B)
C)
D)
E)1
F)2
G)4
H)8

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
57
Find the arc length of the curve given by 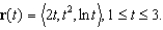
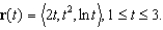

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
58
A particle is traveling along a helix whose vector equation is given by 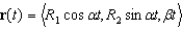 , where
, where 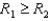 . Find its maximum and minimum speeds.
. Find its maximum and minimum speeds.
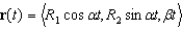 , where
, where 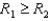 . Find its maximum and minimum speeds.
. Find its maximum and minimum speeds.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
59
Find the curvature of the curve at x = 0.
A)0
B)
C)
D)
E)1
F)2
G)4
H)8
A)0
B)
C)
D)
E)1
F)2
G)4
H)8

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
60
Find the unit tangent vector T(t) to the curve r (t) = when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
61
Find the unit tangent and the unit normal to the graph of the vector function 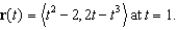
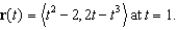

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
62
Find the tangent vector (t) of the function r (t) = when t = .
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
63
Find the equation of the osculating circle of the curve 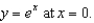
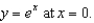

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
64
Find the curvature of the ellipse whose equation is given by 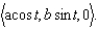
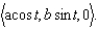

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
65
Find the equation of the osculating circle of the ellipse whose equation is given by 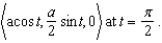
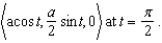

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
66
Find the equation of the osculating circle of the ellipse whose equation is given by 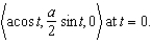
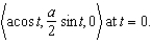

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
67
Use the curvature formula to compute the curvature of a straight line y = mx + b.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
68
Find the curvature of the ellipse whose equation is given by 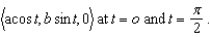
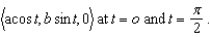

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
69
Find the center of the osculating circle of the curve described by 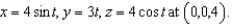
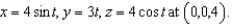

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
70
Consider 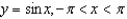 . Determine graphically where the curvature is maximal and minimal.
. Determine graphically where the curvature is maximal and minimal.
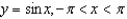 . Determine graphically where the curvature is maximal and minimal.
. Determine graphically where the curvature is maximal and minimal.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
71
Find the derivative of the vector function r (t) = t i + sin t j when t = 0.
A)i
E)-i + j
B)j
F)i - j
C)-i
G)-i - j
D)-j
H)i + j
A)i
E)-i + j
B)j
F)i - j
C)-i
G)-i - j
D)-j
H)i + j

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
72
Suppose C is the curve given by the vector function 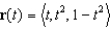 . Find the unit tangent vector, the unit normal vector, and the curvature of C at the point where t = 1.
. Find the unit tangent vector, the unit normal vector, and the curvature of C at the point where t = 1.
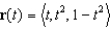 . Find the unit tangent vector, the unit normal vector, and the curvature of C at the point where t = 1.
. Find the unit tangent vector, the unit normal vector, and the curvature of C at the point where t = 1.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
73
Find the center of the osculating circle of the parabola 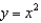 at the origin.
at the origin.
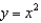 at the origin.
at the origin.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
74
Find the derivative of the vector function r (t) = when t = 1.
A)
B)
C)
D)
E)
F)
G)
H)
A)
B)
C)
D)
E)
F)
G)
H)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
75
Show that if 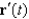 and
and 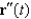 are parallel at some point on the curve described by
are parallel at some point on the curve described by 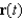 , then the curvature at that point is 0. Give an example of a curve
, then the curvature at that point is 0. Give an example of a curve 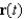 for which
for which 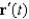 and
and 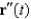 are always parallel.
are always parallel.
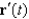 and
and 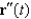 are parallel at some point on the curve described by
are parallel at some point on the curve described by 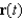 , then the curvature at that point is 0. Give an example of a curve
, then the curvature at that point is 0. Give an example of a curve 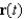 for which
for which 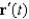 and
and 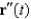 are always parallel.
are always parallel.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
76
Find the curvature of the curve 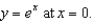
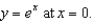

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
77
Find the equation of the plane normal to 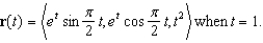
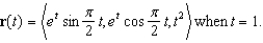

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
78
At what point does the curve 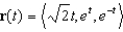 have minimum curvature? What is the minimum curvature?
have minimum curvature? What is the minimum curvature?
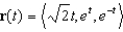 have minimum curvature? What is the minimum curvature?
have minimum curvature? What is the minimum curvature?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
79
At what point does the curve 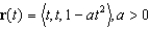 have maximum curvature? What is the maximum curvature?
have maximum curvature? What is the maximum curvature?
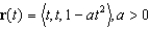 have maximum curvature? What is the maximum curvature?
have maximum curvature? What is the maximum curvature?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck
80
Consider r (t), the vector function describing the curve shown below. Put the curvatures at A, B, and C in order from smallest to largest. 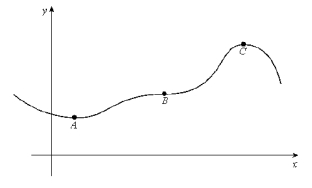


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 111 في هذه المجموعة.
فتح الحزمة
k this deck








