Deck 12: Linear Regression and Correlation
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/166
العب
ملء الشاشة (f)
Deck 12: Linear Regression and Correlation
1
i. In order to visualize the form of the regression equation, we can draw a scatter diagram. ii. The least squares technique minimizes the sum of the squares of the vertical distances between the actual Y values and the predicted values of Y.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
(i), (ii), and (iii) are all correct statements.
2
i. In order to visualize the form of the regression equation, we can draw a scatter diagram. ii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
iii. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
(i) and (ii) are correct statements but not (iii).
3
A scatter diagram is a chart,
A) in which the dependent variable is scaled along the vertical axis.
B) in which the independent variable is scaled along the horizontal axis.
C) that portrays the relationship between two variables.
D) in which the dependent variable is scaled along the vertical axis, the independent variable is scaled along the horizontal axis and portrays the relationship between two variables.
A) in which the dependent variable is scaled along the vertical axis.
B) in which the independent variable is scaled along the horizontal axis.
C) that portrays the relationship between two variables.
D) in which the dependent variable is scaled along the vertical axis, the independent variable is scaled along the horizontal axis and portrays the relationship between two variables.
in which the dependent variable is scaled along the vertical axis, the independent variable is scaled along the horizontal axis and portrays the relationship between two variables.
4
What is the chart called when the paired data (the dependent and independent variables) are plotted?
A) Scatter diagram
B) Bar
C) Pie
D) Linear regression
A) Scatter diagram
B) Bar
C) Pie
D) Linear regression

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
5
In the equation Y' = a + bX, what is Y'?
A) Slope of the line
B) Y intercept
C) Predicted value of Y, given a specific X value
D) Value of Y when X = 0
A) Slope of the line
B) Y intercept
C) Predicted value of Y, given a specific X value
D) Value of Y when X = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
6
i. The least squares technique minimizes the sum of the squares of the vertical distances between the actual Y values and the predicted values of Y. ii. When a regression line has a zero slope, indicating a lack of a relationship, the line is vertical to the x-axis.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
7
i. If we are studying the relationship between high school performance and college performance, and want to predict college performance, high school performance is the dependent variable. ii. A financial advisor is interested in predicting bond yield based on bond term, i.e., one year, two years, etc. The dependent variable is bond term.
iii. The variable used to predict the value of another is called the dependent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The variable used to predict the value of another is called the dependent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
8
In the regression equation, Y' = a + bX, what does the letter "b" represent?
A) Y intercept
B) Slope of the line
C) Any value of the independent variable that is selected
D) Value of Y when X = 0
A) Y intercept
B) Slope of the line
C) Any value of the independent variable that is selected
D) Value of Y when X = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
9
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 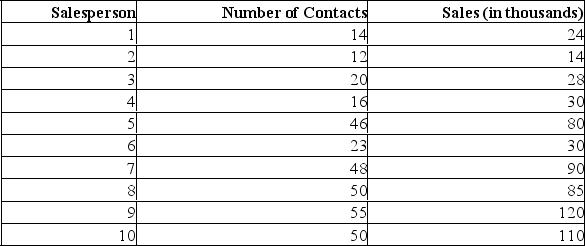
 What is the dependent variable?
What is the dependent variable?
A) Salesperson
B) Number of contacts
C) Amount of sales


 What is the dependent variable?
What is the dependent variable?A) Salesperson
B) Number of contacts
C) Amount of sales

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
10
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. When a regression line has a zero slope, indicating a lack of a relationship, the line is horizontal to the x-axis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. When a regression line has a zero slope, indicating a lack of a relationship, the line is horizontal to the x-axis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
11
What is the variable used to predict the value of another called?
A) Independent
B) Dependent
C) Correlation
D) Determination
A) Independent
B) Dependent
C) Correlation
D) Determination

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
12
Based on the regression equation, we can
A) predict the value of the dependent variable given a value of the independent variable.
B) predict the value of the independent variable given a value of the dependent variable.
C) measure the association between two variables.
A) predict the value of the dependent variable given a value of the independent variable.
B) predict the value of the independent variable given a value of the dependent variable.
C) measure the association between two variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
13
Suppose the least squares regression equation is Y' = 1202 + 1,133X. When X = 3, what does Y' equal?
A) 5,734
B) 8,000
C) 4,601
D) 4,050
A) 5,734
B) 8,000
C) 4,601
D) 4,050

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
14
i. A scatter diagram is a chart that portrays the relationship between two variables. ii. If a scatter diagram shows very little scatter about a straight line drawn through the plots, it indicates a rather weak relationship.
iii. A scatter diagram may be put together using excel or Mega Stat.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. A scatter diagram may be put together using excel or Mega Stat.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
15
i. If we are studying the relationship between high school performance and college performance, and want to predict college performance, high school performance is the independent variable. ii. An economist is interested in predicting the unemployment rate based on gross domestic product. Since the economist is interested in predicting unemployment, the independent variable is gross domestic product.
iii. The variable used to predict the value of another is called the dependent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The variable used to predict the value of another is called the dependent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
16
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 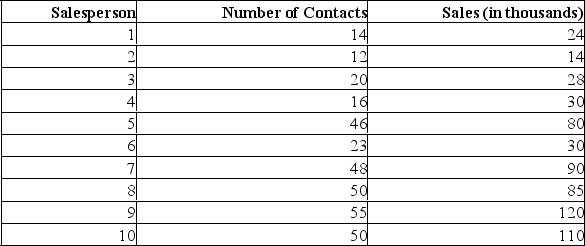
 What is the independent variable?
What is the independent variable?
A) Salesperson
B) Number of contacts
C) Amount of sales


 What is the independent variable?
What is the independent variable?A) Salesperson
B) Number of contacts
C) Amount of sales

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
17
i. If we are studying the relationship between high school performance and college performance, and want to predict college performance, high school performance is the independent variable. ii. A financial advisor is interested in predicting bond yield based on bond term, i.e., one year, two years, etc. The dependent variable is bond yield.
iii. The variable used to predict the value of another is called the independent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The variable used to predict the value of another is called the independent variable.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
18
In the regression equation, Y' = a + bX, what does the letter "a" represent?
A) Y intercept
B) Slope of the line
C) Any value of the independent variable that is selected
A) Y intercept
B) Slope of the line
C) Any value of the independent variable that is selected

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
19
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. When a regression line has a zero slope, indicating a lack of a relationship, the line is horizontal to the x-axis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. When a regression line has a zero slope, indicating a lack of a relationship, the line is horizontal to the x-axis.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
20
i. In order to visualize the form of the regression equation, we can draw a scatter diagram. ii. When a regression line has a zero slope, indicating a lack of a relationship, the line is vertical to the x-axis.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. In regression analysis, the predicted value of Y' rarely agrees exactly with the actual Y value, i.e., we expect some prediction error.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
21
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. The least squares technique minimizes the sum of the squares of the vertical distances between the actual Y values and the predicted values of Y.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The least squares technique minimizes the sum of the squares of the vertical distances between the actual Y values and the predicted values of Y.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
22
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 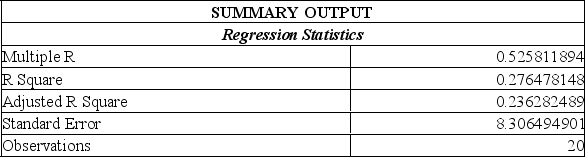
 From this printout you determine:
From this printout you determine:
A) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences.
B) for each additional year of age, we can expect the number of days of absence to decrease by 0.2 days.
C) almost 67% of the variation in the number of absent days can be explained by the variation in the employee's ages.
D) when tested at the 2% level of significance, there is relationship between an employee's age and the number of days of work absences. For each additional year of age, we can expect the number of days of absence to decrease by 0.2 days.
E) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences. Almost 67% of the variation in the number of absent days can be explained by the variation in the employee's ages.

 From this printout you determine:
From this printout you determine:A) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences.
B) for each additional year of age, we can expect the number of days of absence to decrease by 0.2 days.
C) almost 67% of the variation in the number of absent days can be explained by the variation in the employee's ages.
D) when tested at the 2% level of significance, there is relationship between an employee's age and the number of days of work absences. For each additional year of age, we can expect the number of days of absence to decrease by 0.2 days.
E) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences. Almost 67% of the variation in the number of absent days can be explained by the variation in the employee's ages.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
23
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 
 From this printout you determine:
From this printout you determine:
A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 8.3x.
D) the regression equation is Y = 23.57 x - 0.45.
E) the employee age is the independent variable; the regression equation is Y = 23.57 + 0.45x.

 From this printout you determine:
From this printout you determine:A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 8.3x.
D) the regression equation is Y = 23.57 x - 0.45.
E) the employee age is the independent variable; the regression equation is Y = 23.57 + 0.45x.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
24
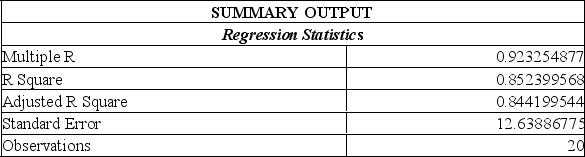
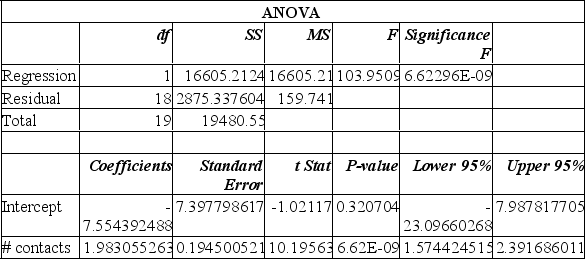
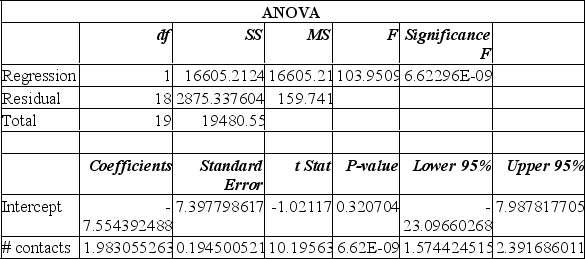
Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Excel printout is shown below. 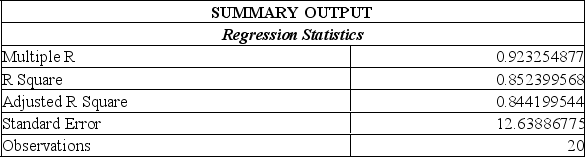
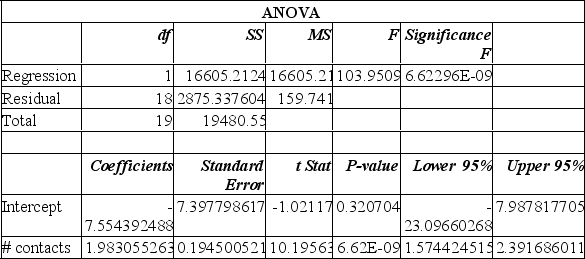 From this printout you determine:
From this printout you determine:
A) there is a very weak relationship between the # of contacts and the sales $.
B) there is a very strong relationship between the # of contacts and the sales $.
C) the regression equation is y = 1.98 x + 7.55.
D) the regression equation is y = -7.55 x + 1.98.

 From this printout you determine:
From this printout you determine:A) there is a very weak relationship between the # of contacts and the sales $.
B) there is a very strong relationship between the # of contacts and the sales $.
C) the regression equation is y = 1.98 x + 7.55.
D) the regression equation is y = -7.55 x + 1.98.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
25
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 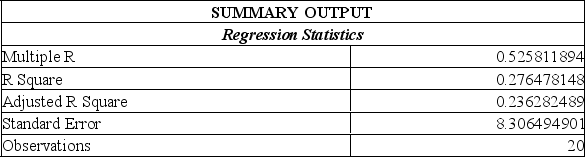
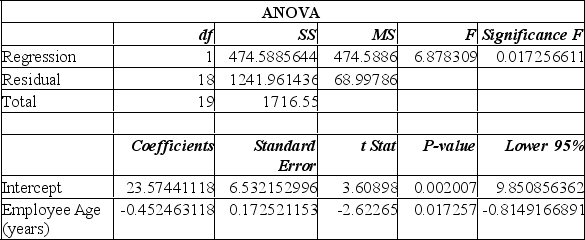 From this printout you determine:
From this printout you determine:
A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 0.45x.
D) the regression equation is Y = 23.57 x -0.45.
E) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x.

 From this printout you determine:
From this printout you determine:A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 0.45x.
D) the regression equation is Y = 23.57 x -0.45.
E) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
26
The slope of the regression line:
A) represents the average change in Y' for each change of one unit in the independent variable, X.
B) represents the average change in X for each change of one unit in the dependent variable, Y.
C) represents the change in Y' for each change of one unit in the independent variable, X.
A) represents the average change in Y' for each change of one unit in the independent variable, X.
B) represents the average change in X for each change of one unit in the dependent variable, Y.
C) represents the change in Y' for each change of one unit in the independent variable, X.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
27
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 
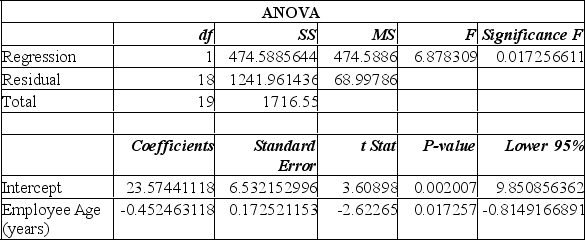 From this printout you determine:
From this printout you determine:
A) the y-intercept of 23 makes no sense.
B) for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
C) for each additional year of age, we can expect the number of days of absence to decrease by 0.45 days.
D) the y-intercept of 23 makes no sense; for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
E) the y-intercept of 23 makes no sense; for each additional year of age, we can expect the number of days of absence to decrease by 0.45 days.

 From this printout you determine:
From this printout you determine:A) the y-intercept of 23 makes no sense.
B) for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
C) for each additional year of age, we can expect the number of days of absence to decrease by 0.45 days.
D) the y-intercept of 23 makes no sense; for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
E) the y-intercept of 23 makes no sense; for each additional year of age, we can expect the number of days of absence to decrease by 0.45 days.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
28
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. The equation for a straight line going through the plots on a scatter diagram is called a regression equation. It is alternately called an estimating equation and a predicting equation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The equation for a straight line going through the plots on a scatter diagram is called a regression equation. It is alternately called an estimating equation and a predicting equation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
29
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 
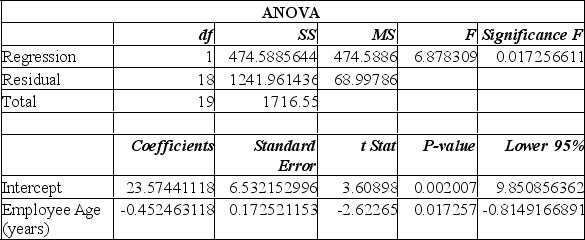 From this printout you determine:
From this printout you determine:
A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the older the employee the more days they are absent from work.
D) the intercept of 23 indicates the most days absent.

 From this printout you determine:
From this printout you determine:A) the employee age is the dependent variable.
B) the employee age is the independent variable.
C) the older the employee the more days they are absent from work.
D) the intercept of 23 indicates the most days absent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
30
Given the following five points: (-2,0), (-1,0), (0,1), (1,1), and (2,3). What is the slope of the line?
A) 0.0
B) 0.5
C) 0.6
D) 0.7
A) 0.0
B) 0.5
C) 0.6
D) 0.7

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
31
In the least squares equation, Y' = 10 + 20X the value of 20 indicates
A) the Y intercept.
B) for each unit increased in X, Y increases by 20.
C) for each unit increased in Y, X increases by 20.
A) the Y intercept.
B) for each unit increased in X, Y increases by 20.
C) for each unit increased in Y, X increases by 20.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
32
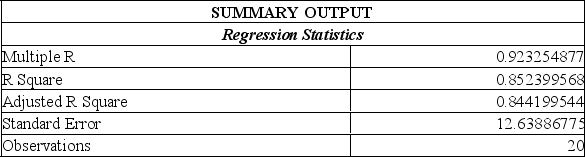
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 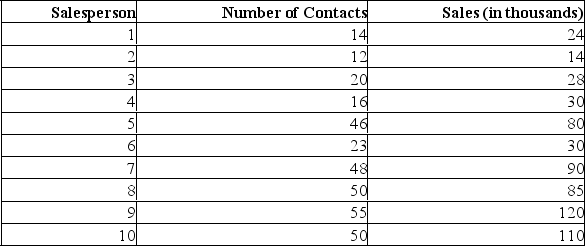
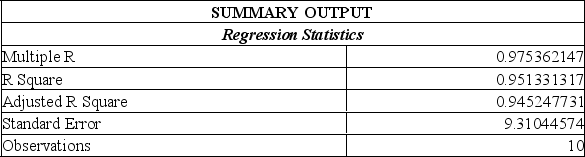
 What is the Y-intercept of the linear equation?
What is the Y-intercept of the linear equation?
A) -12.201
B) 2.1946
C) -2.1946
D) 12.201


 What is the Y-intercept of the linear equation?
What is the Y-intercept of the linear equation?A) -12.201
B) 2.1946
C) -2.1946
D) 12.201

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
33
Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Excel printout is shown below. 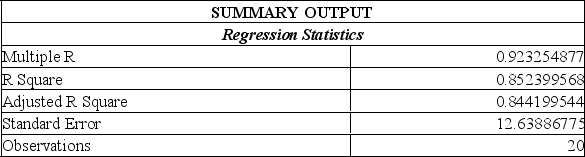
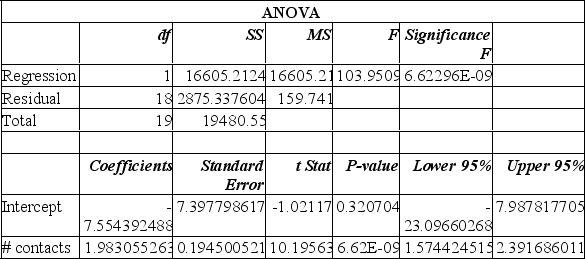 This model predicts that with 25 sales contacts, sales will be:
This model predicts that with 25 sales contacts, sales will be:
A) $49 576.
B) $42 022.
C) $190 843.
D) $19 429.
E) $16 605.

 This model predicts that with 25 sales contacts, sales will be:
This model predicts that with 25 sales contacts, sales will be:A) $49 576.
B) $42 022.
C) $190 843.
D) $19 429.
E) $16 605.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
34
Assume the least squares equation is Y' = 10 + 20X. What does the value of 10 in the equation indicate?
A) Y intercept
B) For each unit increased in Y, X increases by 10
C) For each unit increased in X, Y increases by 10
A) Y intercept
B) For each unit increased in Y, X increases by 10
C) For each unit increased in X, Y increases by 10

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
35
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. A regression equation may be determined using a mathematical method called the.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. A regression equation may be determined using a mathematical method called the.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
36
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 
 From this printout you determine:
From this printout you determine:
A) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences.
B) for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
C) almost 53% of the variation in the number of absent days can be explained by the variation in the employees ages.
D) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences; for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.

 From this printout you determine:
From this printout you determine:A) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences.
B) for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.
C) almost 53% of the variation in the number of absent days can be explained by the variation in the employees ages.
D) when tested at the 2% level of significance, there is no relationship between an employee's age and the number of days of work absences; for each additional year of age, we can expect the number of days of absence to increase by 0.45 days.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
37
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Excel results are summarized below: 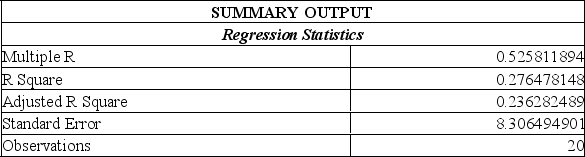
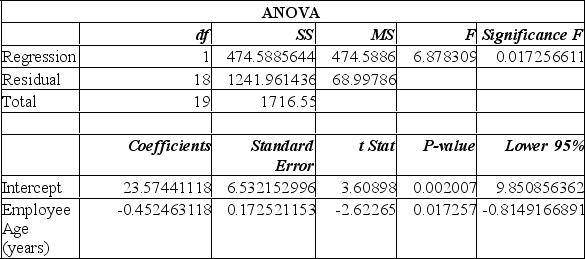 From this printout you determine:
From this printout you determine:
A) the y-intercept of 23 makes no sense.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 0.45x.
D) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x.
E) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x, however the y-intercept of 23 makes no sense.

 From this printout you determine:
From this printout you determine:A) the y-intercept of 23 makes no sense.
B) the employee age is the independent variable.
C) the regression equation is Y = 23.57 - 0.45x.
D) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x.
E) the employee age is the independent variable; the regression equation is Y = 23.57 - 0.45x, however the y-intercept of 23 makes no sense.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
38
Given the following five points: (-2,0), (-1,0), (0,1), (1,1), and (2,3). What is the Y intercept?
A) 0.0
B) 0.7
C) 1.0
D) 1.5
A) 0.0
B) 0.7
C) 1.0
D) 1.5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
39
The partial Mega Stat output below is regression analysis of the relationship between annual payroll and number of wins in a season for 28 teams in professional sports. The purpose of the analysis is to predict the number of wins when given an annual payroll in $millions. Although technically not a sample, the baseball data below will be treated as a convenience sample of all major league professional sports. 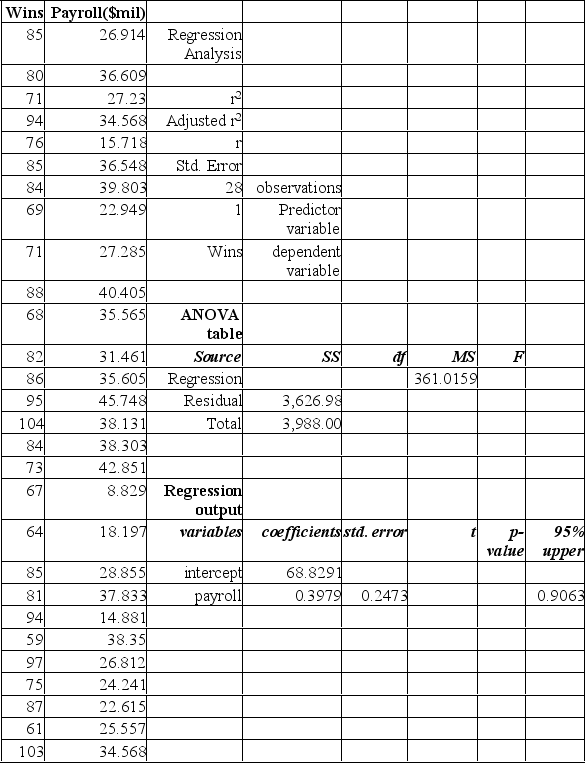 Refer to the printout above. The regression equation is:
Refer to the printout above. The regression equation is:
A)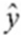 = 2,049 + 68.8291x
= 2,049 + 68.8291x
B)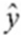 = 82.5157 + 28.2049x
= 82.5157 + 28.2049x
C)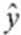 = 28.2049 + 7.5888x
= 28.2049 + 7.5888x
D)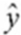 = 82.5157 + 7.5888x
= 82.5157 + 7.5888x
E)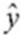 = 7.5888 + 28.2049x
= 7.5888 + 28.2049x
 Refer to the printout above. The regression equation is:
Refer to the printout above. The regression equation is:A)
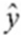 = 2,049 + 68.8291x
= 2,049 + 68.8291xB)
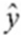 = 82.5157 + 28.2049x
= 82.5157 + 28.2049xC)
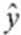 = 28.2049 + 7.5888x
= 28.2049 + 7.5888xD)
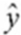 = 82.5157 + 7.5888x
= 82.5157 + 7.5888xE)
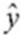 = 7.5888 + 28.2049x
= 7.5888 + 28.2049x
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
40
i. The technique used to measure the strength of the relationship between two sets of variables using the coefficient of correlation and the coefficient of determination is called regression analysis. ii. In order to visualize the form of the regression equation, we can draw a scatter diagram.
iii. A line found using the is the best-fitting line because the sum of the squares of the vertical deviations between the actual and estimated values is minimized.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. A line found using the is the best-fitting line because the sum of the squares of the vertical deviations between the actual and estimated values is minimized.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
41
i. The purpose of correlation analysis is to find how strong the relationship is between two variables. ii. A coefficient of correlation of -0.96 indicates a very weak negative correlation.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
42
We have collected price per share and dividend information from a sample of 30 companies. 
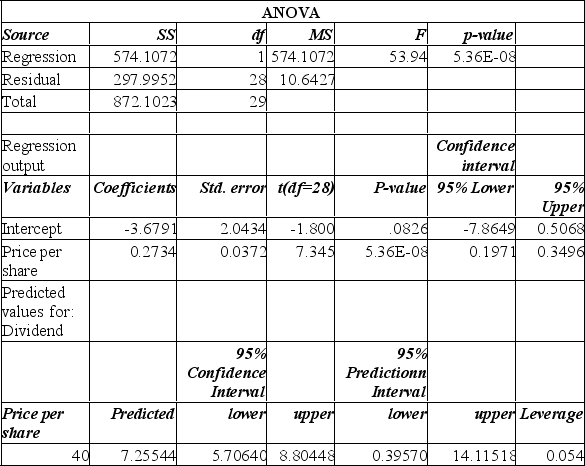 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:
A) for each additional dollar in stock price, we can anticipate an additional $2.73 in dividend.
B) for each additional dollar in stock price, we can anticipate a drop of $2.41 in dividend.
C) when the stock price is zero, we can anticipate a dividend of $0.27. This value, however, makes no sense.
D) when the stock price is zero, we can anticipate a dividend of $-3.68. This value, however, makes no sense.
E) when the dividends are zero, we can anticipate a negative share price.

 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:A) for each additional dollar in stock price, we can anticipate an additional $2.73 in dividend.
B) for each additional dollar in stock price, we can anticipate a drop of $2.41 in dividend.
C) when the stock price is zero, we can anticipate a dividend of $0.27. This value, however, makes no sense.
D) when the stock price is zero, we can anticipate a dividend of $-3.68. This value, however, makes no sense.
E) when the dividends are zero, we can anticipate a negative share price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
43
i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
44
i. A correlation coefficient of -1 or +1 indicates perfect correlation. ii. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak.
iii. Coefficients of -0.91 and +0.91 have equal strength.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. Coefficients of -0.91 and +0.91 have equal strength.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
45
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 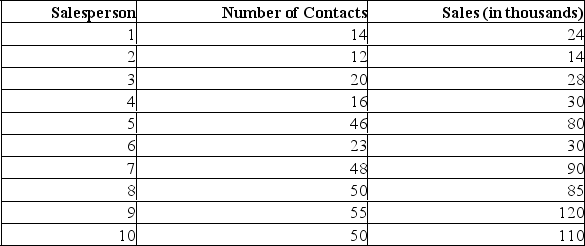

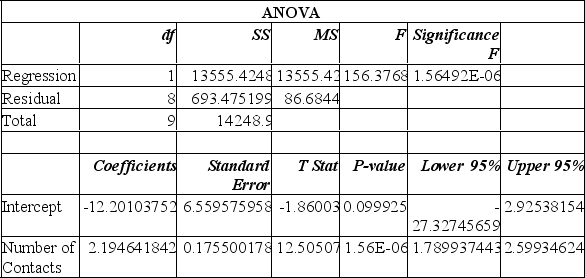 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:
A) for each additional contact made, the salesperson can anticipate an additional $2,195 in sales.
B) for each additional contact made, the salesperson can anticipate a drop of $12,201 in sales.
C) when no contacts are made, the salesperson can anticipate sales of $12,201.
D) when no contacts are made, the salesperson can anticipate negative sales-therefore the regression model doesn't make sense for no contacts.
E) when no contacts are made, the salesperson can anticipate sales of $2,195.


 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:A) for each additional contact made, the salesperson can anticipate an additional $2,195 in sales.
B) for each additional contact made, the salesperson can anticipate a drop of $12,201 in sales.
C) when no contacts are made, the salesperson can anticipate sales of $12,201.
D) when no contacts are made, the salesperson can anticipate negative sales-therefore the regression model doesn't make sense for no contacts.
E) when no contacts are made, the salesperson can anticipate sales of $2,195.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
46
i. A correlation coefficient of -1 or +1 indicates perfect correlation. ii. The strength of the correlation between two variables depends on the sign of the coefficient of correlation.
iii. If the coefficient of correlation is -0.90, the coefficient of determination is -0.81.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) is a correct statement but not (ii) or (iii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. If the coefficient of correlation is -0.90, the coefficient of determination is -0.81.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) is a correct statement but not (ii) or (iii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
47
We have collected price per share and dividend information from a sample of 30 companies. 
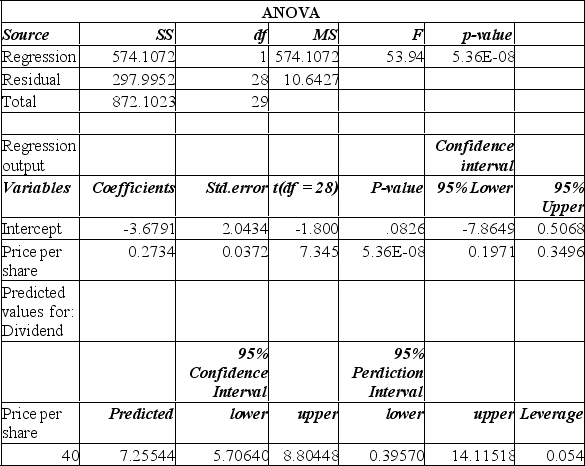 The slope in this instance indicates:
The slope in this instance indicates:
A) for each additional dollar in stock price, we can anticipate an additional $2.73 in dividend.
B) for each additional dollar in stock price, we can anticipate an additional $3.68 in dividend.
C) for each additional dollar in stock price, we can anticipate an additional $0.27 in dividend.
D) for each additional dollar in dividend, we can anticipate an additional $2.71 in stock price.
E) for each additional dollar in dividend, we can anticipate a drop of $3.68 in stock price.

 The slope in this instance indicates:
The slope in this instance indicates:A) for each additional dollar in stock price, we can anticipate an additional $2.73 in dividend.
B) for each additional dollar in stock price, we can anticipate an additional $3.68 in dividend.
C) for each additional dollar in stock price, we can anticipate an additional $0.27 in dividend.
D) for each additional dollar in dividend, we can anticipate an additional $2.71 in stock price.
E) for each additional dollar in dividend, we can anticipate a drop of $3.68 in stock price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
48
i. The strength of the correlation between two variables depends on the sign of the coefficient of correlation. ii. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak.
iii. Coefficients of -0.91 and + 0.91 have equal strength.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. Coefficients of -0.91 and + 0.91 have equal strength.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
49
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 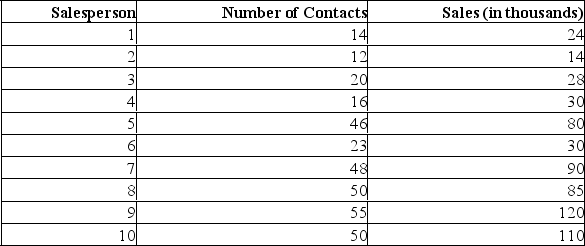

 The slope in this instance indicates:
The slope in this instance indicates:
A) for each additional contact made, the salesperson can anticipate an additional $2195 in sales.
B) for each additional contact made, the salesperson can anticipate an additional $2.19 in sales.
C) for each additional contact made, the salesperson can anticipate an additional $12,201 in sales.
D) for each additional contact made, the salesperson can anticipate a drop of $12,201 in sales.
E) for each additional sale made, the salesperson can anticipate an additional 2 contacts are needed.


 The slope in this instance indicates:
The slope in this instance indicates:A) for each additional contact made, the salesperson can anticipate an additional $2195 in sales.
B) for each additional contact made, the salesperson can anticipate an additional $2.19 in sales.
C) for each additional contact made, the salesperson can anticipate an additional $12,201 in sales.
D) for each additional contact made, the salesperson can anticipate a drop of $12,201 in sales.
E) for each additional sale made, the salesperson can anticipate an additional 2 contacts are needed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
50
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 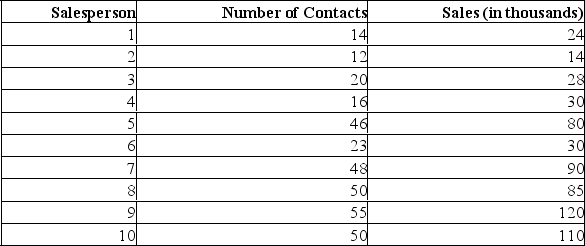
 What is the slope of the linear equation?
What is the slope of the linear equation?
A) -12.201
B) 12.201
C) 2.1946
D) -2.1946


 What is the slope of the linear equation?
What is the slope of the linear equation?A) -12.201
B) 12.201
C) 2.1946
D) -2.1946

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
51
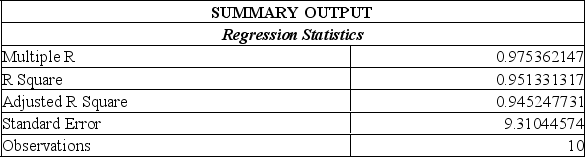
We have collected price per share and dividend information from a sample of 30 companies. Using the Mega Stat printout, determine the regression equation that predicts the dividend from the stock's selling price. 
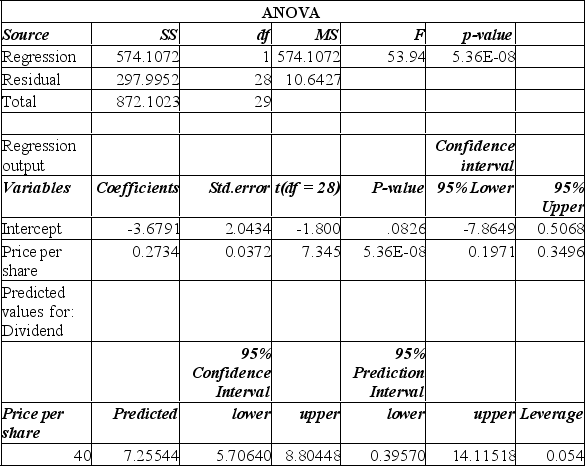
A) Y = 0.27 + 3.68x
B) Y = 0.27x + 3.68
C) Y = -3.68 + 0.27x
D) Y = -0.27x - 3.68
E) Y =0.27x-3.6791


A) Y = 0.27 + 3.68x
B) Y = 0.27x + 3.68
C) Y = -3.68 + 0.27x
D) Y = -0.27x - 3.68
E) Y =0.27x-3.6791

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
52
i. A coefficient of correlation r close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. The coefficient of determination is the proportion of the total variation in the dependent variable Y that is explained or accounted for by its relationship with the independent variable X.
iii. If the coefficient of correlation is -0.90, the coefficient of determination is -0.81.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. If the coefficient of correlation is -0.90, the coefficient of determination is -0.81.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
53
i. The purpose of correlation analysis is to find how strong the relationship is between two variables. ii. A correlation coefficient of -1 or + 1 indicates perfect correlation.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
54
Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Excel printout is shown below. 
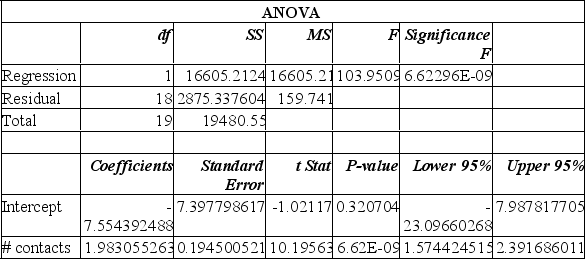 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:
A) for each additional contact made, the salesperson can anticipate an additional $193 in sales.
B) for each additional contact made, the salesperson can anticipate a drop of $1983 in sales.
C) when no contacts are made, the salesperson can anticipate sales of $7554.
D) when no contacts are made, the salesperson can anticipate sales of $1983.
E) when no contacts are made, the salesperson can anticipate negative sales - therefore the regression model doesn't make sense for no contacts.

 The y-intercept in this instance suggests:
The y-intercept in this instance suggests:A) for each additional contact made, the salesperson can anticipate an additional $193 in sales.
B) for each additional contact made, the salesperson can anticipate a drop of $1983 in sales.
C) when no contacts are made, the salesperson can anticipate sales of $7554.
D) when no contacts are made, the salesperson can anticipate sales of $1983.
E) when no contacts are made, the salesperson can anticipate negative sales - therefore the regression model doesn't make sense for no contacts.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
55
Information was collected from employee records to determine whether there is an association between an employee's age and the number or workdays they miss. Partial excel results are summarized below from two different samples: 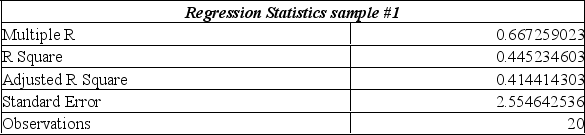
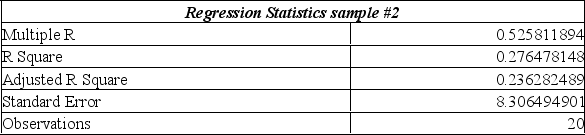 Given this information alone, would you decide to continue with the regression analysis for sample #1 or #2 or both?
Given this information alone, would you decide to continue with the regression analysis for sample #1 or #2 or both?
A) Continue with both samples, because the sample sizes are over 15.
B) Continue with sample #1 because the multiple r value is larger than that of sample #2.
C) Continue with sample #2 because the multiple r value is larger than that of sample #1.
D) Don't continue with either sample, because the standard error values are more than 2.
E) Don't continue with either sample, because the sample sizes are too small to be of use.

 Given this information alone, would you decide to continue with the regression analysis for sample #1 or #2 or both?
Given this information alone, would you decide to continue with the regression analysis for sample #1 or #2 or both?A) Continue with both samples, because the sample sizes are over 15.
B) Continue with sample #1 because the multiple r value is larger than that of sample #2.
C) Continue with sample #2 because the multiple r value is larger than that of sample #1.
D) Don't continue with either sample, because the standard error values are more than 2.
E) Don't continue with either sample, because the sample sizes are too small to be of use.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
56
Data is collected from 20 sales people in order to verify that the more contacts made with potential clients, the greater the sales volume. The Excel printout is shown below. 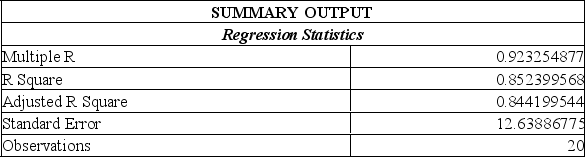
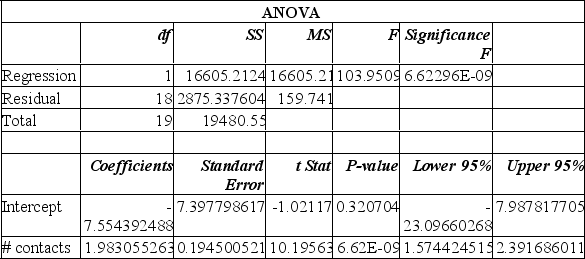 The slope in this instance indicates:
The slope in this instance indicates:
A) for each additional contact made, the salesperson can anticipate an additional $1983 in sales.
B) for each additional contact made, the salesperson can anticipate an additional $1.98 in sales.
C) for each additional contact made, the salesperson can anticipate an additional $7,554 in sales.
D) for each additional contact made, the salesperson can anticipate a drop of $7,554 in sales.
E) for each additional sale made, the salesperson can anticipate an additional 2 contacts are needed.

 The slope in this instance indicates:
The slope in this instance indicates:A) for each additional contact made, the salesperson can anticipate an additional $1983 in sales.
B) for each additional contact made, the salesperson can anticipate an additional $1.98 in sales.
C) for each additional contact made, the salesperson can anticipate an additional $7,554 in sales.
D) for each additional contact made, the salesperson can anticipate a drop of $7,554 in sales.
E) for each additional sale made, the salesperson can anticipate an additional 2 contacts are needed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
57
i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. A coefficient of correlation of -0.96 indicates a very weak negative correlation.
iii. The coefficient of determination can only be positive.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The coefficient of determination can only be positive.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
58
The partial mega stat output below is regression analysis of the relationship between annual payroll and number of wins in a season for 28 teams in professional sports. The purpose of the analysis is to predict the number of wins when given an annual payroll in $millions. Although technically not a sample, the baseball data below will be treated as a convenience sample of all major league professional sports.  Refer to the printout above. The regression equation is:
Refer to the printout above. The regression equation is:
A)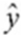 = 0.379 + 68.8291x
= 0.379 + 68.8291x
B) = 68.8291 + 0.3979x
= 68.8291 + 0.3979x
C)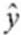 = 0.2473 + 0.3979x
= 0.2473 + 0.3979x
D)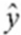 = 68.8291 + 0.2473x
= 68.8291 + 0.2473x
E)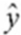 = 0.2473 + 68.8291x
= 0.2473 + 68.8291x
 Refer to the printout above. The regression equation is:
Refer to the printout above. The regression equation is:A)
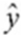 = 0.379 + 68.8291x
= 0.379 + 68.8291xB)
 = 68.8291 + 0.3979x
= 68.8291 + 0.3979xC)
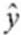 = 0.2473 + 0.3979x
= 0.2473 + 0.3979xD)
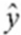 = 68.8291 + 0.2473x
= 68.8291 + 0.2473xE)
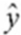 = 0.2473 + 68.8291x
= 0.2473 + 68.8291x
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
59
A sales manager for an advertising agency believes there is a relationship between the number of contacts and the amount of the sales. To verify this belief, the following data was collected: 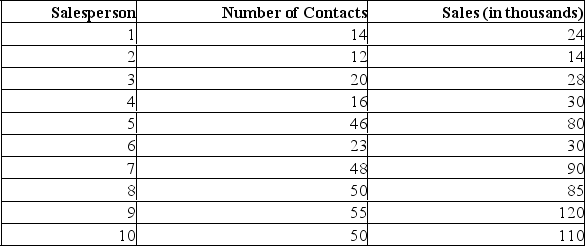
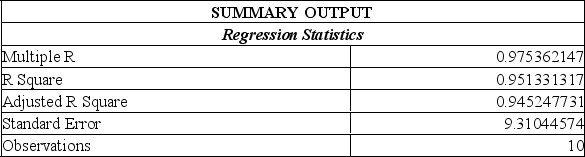
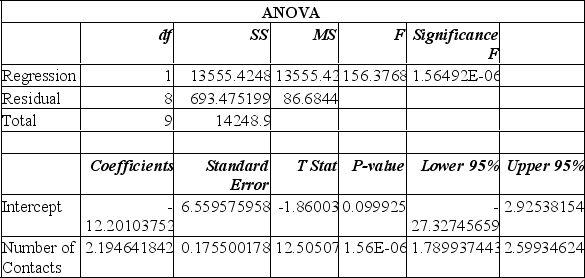 What is the regression equation?
What is the regression equation?
A) Y' = 2.1946 - 12.201X
B) Y' = -12.201 + 2.1946X
C) Y' = 12.201 + 2.1946X
D) Y' = 2.1946 + 12.201X


 What is the regression equation?
What is the regression equation?A) Y' = 2.1946 - 12.201X
B) Y' = -12.201 + 2.1946X
C) Y' = 12.201 + 2.1946X
D) Y' = 2.1946 + 12.201X

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
60
The partial Mega Stat output below is regression analysis of the relationship between annual payroll and number of wins in a season for 28 teams in professional sports. The purpose of the analysis is to predict the number of wins when given an annual payroll in $millions. Although technically not a sample, the baseball data below will be treated as a convenience sample of all major league professional sports. 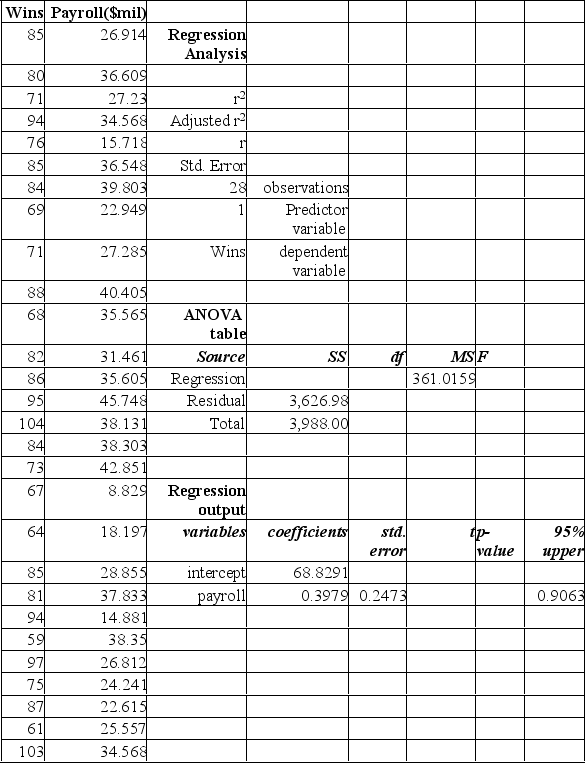 Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
A) 10
B) 69
C) 79
D) 74
E) 64
 Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)A) 10
B) 69
C) 79
D) 74
E) 64

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
61
i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. A coefficient of correlation of -0.96 indicates a very weak negative correlation.
iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
62
i. If the value of r is -0.96, what does this indicate about the dependent variable as the independent variable increases? ii. What is the value of the correlation coefficient if there is perfect correlation?
iii. If the dependent variable is measured in dollars, in what units is the standard error of estimate measured?
A) it increases; zero; dollars squared
B) it decreases; +/-1.0; dollars squared
C) it increases; 1.0; dollars ($)
D) it decreases; +/-1.0; dollars ($)
E) it decreases; zero; dollars
iii. If the dependent variable is measured in dollars, in what units is the standard error of estimate measured?
A) it increases; zero; dollars squared
B) it decreases; +/-1.0; dollars squared
C) it increases; 1.0; dollars ($)
D) it decreases; +/-1.0; dollars ($)
E) it decreases; zero; dollars

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
63
i. What is the range of values that the coefficient of determination can assume? ii. What is a measure of the scatter of observed values around the regression line called?
iii. If the correlation between sales and advertising is +0.6, what percent of the variation in sales can be attributed to advertising?
A) 0% to 1%; standard variation;36%.
B) both positive and negative values; standard deviation;6%.
C) 0% to 100%; standard error of the estimate; 36%.
D) 0% to 100%; standard variation;36%.
E) both positive and negative values; standard error of the estimate; 36%.
iii. If the correlation between sales and advertising is +0.6, what percent of the variation in sales can be attributed to advertising?
A) 0% to 1%; standard variation;36%.
B) both positive and negative values; standard deviation;6%.
C) 0% to 100%; standard error of the estimate; 36%.
D) 0% to 100%; standard variation;36%.
E) both positive and negative values; standard error of the estimate; 36%.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
64
What is the range of values for a coefficient of correlation?
A) 0 to +1.0
B) -3 to + 3 inclusive
C) -1.0 to +1.0 inclusive
D) Unlimited range
A) 0 to +1.0
B) -3 to + 3 inclusive
C) -1.0 to +1.0 inclusive
D) Unlimited range

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
65
i. If the coefficient of determination is 0.81, what is the coefficient of correlation? ii. If the coefficient of correlation is -0.81, what is the coefficient of determination?
iii. If the dependent variable is measured in dollars, in what units is the standard error of estimate measured?
A) +/-0.9; 0.6561; dollars squared.
B) +/-0.9; 0.6561; dollars.
C) 0.6561; 0.9; dollars.
D) 0.6561; +/-0.9; dollars squared.
E) 0.9; -0.9; dollars squared.
iii. If the dependent variable is measured in dollars, in what units is the standard error of estimate measured?
A) +/-0.9; 0.6561; dollars squared.
B) +/-0.9; 0.6561; dollars.
C) 0.6561; 0.9; dollars.
D) 0.6561; +/-0.9; dollars squared.
E) 0.9; -0.9; dollars squared.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
66
Which of the following statements regarding the coefficient of correlation is true?
A) It ranges from -1.0 to + 1.0 inclusive.
B) It measures the strength of the relationship between two variables.
C) A value of 0.00 indicates two variables are not related.
D) It ranges from -1.0 to + 1.0 inclusive;0.00 indicates the two variables are not related. It measures the strength of the relationship between two variables.
A) It ranges from -1.0 to + 1.0 inclusive.
B) It measures the strength of the relationship between two variables.
C) A value of 0.00 indicates two variables are not related.
D) It ranges from -1.0 to + 1.0 inclusive;0.00 indicates the two variables are not related. It measures the strength of the relationship between two variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
67
i. Perfect correlation means that the scatter diagram will appear as a straight line ii. If the coefficient of correlation is 0.80, the coefficient of determination is 0.64.
iii. The coefficient of determination can assume values between 0% and 100%
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The coefficient of determination can assume values between 0% and 100%
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
68
What does a coefficient of correlation of 0.70 infer?
A) Almost no correlation because 0.70 is close to 1.0.
B) 70% of the variation in one variable is explained by the other.
C) Coefficient of determination is 0.49.
D) Coefficient of non determination is 0.30.
A) Almost no correlation because 0.70 is close to 1.0.
B) 70% of the variation in one variable is explained by the other.
C) Coefficient of determination is 0.49.
D) Coefficient of non determination is 0.30.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
69
i. The coefficient of determination can only be positive. ii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
70
i. The strength of the correlation between two variables depends on the sign of the coefficient of correlation. ii. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak.
iii. The coefficient of determination is found by taking the square root of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) is a correct statement but not (i) or (iii).
E) (i), (ii), and (iii) are all false statements.
iii. The coefficient of determination is found by taking the square root of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) is a correct statement but not (i) or (iii).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
71
The partial Mega Stat output below is regression analysis of the relationship between annual payroll and number of wins in a season for 28 teams in professional sports. The purpose of the analysis is to predict the number of wins when given an annual payroll in $millions. Although technically not a sample, the baseball data below will be treated as a convenience sample of all major league professional sports. 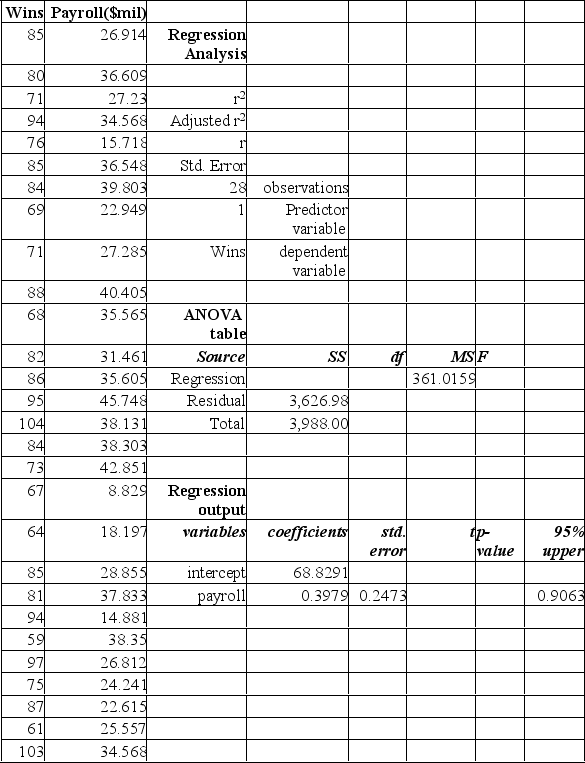 Refer to the printout above. How many independent variables?
Refer to the printout above. How many independent variables?
A) 1
B) 2
C) 9
D) 10
E) 11
 Refer to the printout above. How many independent variables?
Refer to the printout above. How many independent variables?A) 1
B) 2
C) 9
D) 10
E) 11

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
72
The partial Mega Stat output below is regression analysis of the relationship between annual payroll and number of wins in a season for 28 teams in professional sports. The purpose of the analysis is to predict the number of wins when given an annual payroll in $millions. Although technically not a sample, the baseball data below will be treated as a convenience sample of all major league professional sports. 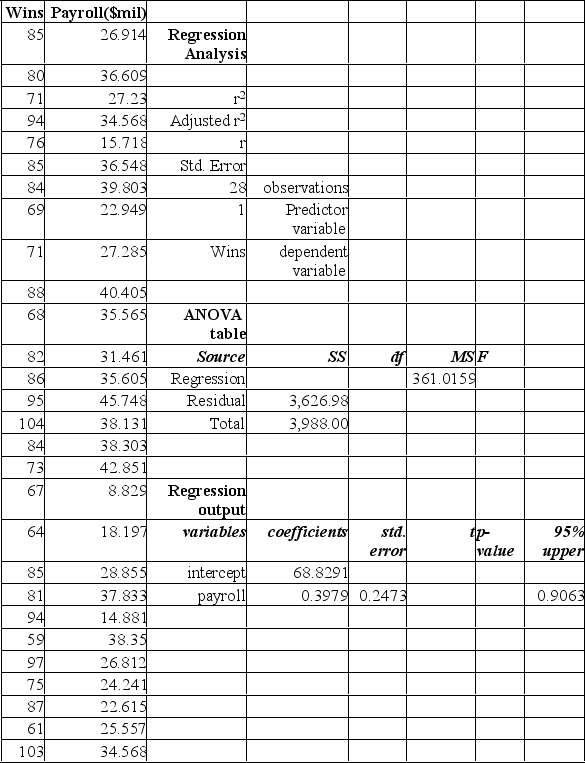 Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
A) 10
B) 69
C) 79
D) 74
E) 64
 Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)
Refer to the printout above. Predict the number of wins for a team with PAYROLL = 25(million) (nearest whole number)A) 10
B) 69
C) 79
D) 74
E) 64

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
73
i. Correlation analysis is a group of statistical techniques used to measure the strength of the relationship (correlation) between two variables. ii. A correlation coefficient of -1 or +1 indicates perfect correlation.
iii. The strength of the correlation between two variables depends on the sign of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The strength of the correlation between two variables depends on the sign of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
74
i. The coefficient of correlation is a measure of the strength of relationship between two variables. ii. The coefficient of determination can only be positive.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
75
i. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak. ii. Coefficients of -0.91 and +0.91 have equal strength.
iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. If the coefficient of correlation is 0.68, the coefficient of determination is 0.4624.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
76
What is the difference between a confidence interval and a prediction interval for the dependent variable in correlation analysis?
A) A prediction interval reports the mean value of Y for a given X, whereas a confidence interval reports the range of values of Y for a particular value of X.
B) A confidence interval reports the mean value of Y for a given X, whereas a prediction interval reports the range of values of Y for a particular value of X.
C) A confidence interval reports the value of Y for a given X, whereas a prediction interval reports the value of Y for a particular value of X.
A) A prediction interval reports the mean value of Y for a given X, whereas a confidence interval reports the range of values of Y for a particular value of X.
B) A confidence interval reports the mean value of Y for a given X, whereas a prediction interval reports the range of values of Y for a particular value of X.
C) A confidence interval reports the value of Y for a given X, whereas a prediction interval reports the value of Y for a particular value of X.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
77
i. The purpose of correlation analysis is to find how strong the relationship is between two variables. ii. A coefficient of correlation close to 0 (say, 0.08) shows that the relationship between two variables is quite weak.
iii. The strength of the correlation between two variables depends on the sign of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The strength of the correlation between two variables depends on the sign of the coefficient of correlation.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
78
i. If the coefficient of correlation is 0.80, what is the coefficient of determination? ii. What is a measure of the scatter of observed values around the regression line called?
iii. If the correlation between sales and advertising is + 0.6, what percent of the variation in sales can be attributed to advertising?
A) 0.4; standard deviation; 0.3.
B) 0.64; standard error of the estimate; 36%.
C) 0.64; standard error of the estimate; 60%.
D) 0.08; variation; 36%.
E) 0.4; standard error of the estimate; 60%.
iii. If the correlation between sales and advertising is + 0.6, what percent of the variation in sales can be attributed to advertising?
A) 0.4; standard deviation; 0.3.
B) 0.64; standard error of the estimate; 36%.
C) 0.64; standard error of the estimate; 60%.
D) 0.08; variation; 36%.
E) 0.4; standard error of the estimate; 60%.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
79
i. If the coefficient of correlation is -0.81, what is the coefficient of determination? ii. If the value of r is -0.96, what does this indicate about the dependent variable as the independent variable increases?
iii. If the correlation between sales and advertising is +0.6, what percent of the variation in sales can be attributed to advertising?
A) 0.6561; it decreases;36%.
B) 0.6561; it increases;36%.
C) 0.6561; it decreases;60%.
D) 0.9; it decreases;6%.
E) 0.9; it increases;60%.
iii. If the correlation between sales and advertising is +0.6, what percent of the variation in sales can be attributed to advertising?
A) 0.6561; it decreases;36%.
B) 0.6561; it increases;36%.
C) 0.6561; it decreases;60%.
D) 0.9; it decreases;6%.
E) 0.9; it increases;60%.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck
80
i. The coefficient of determination is the proportion of the total variation in the dependent variable Y that is explained or accounted for by its relationship with the independent variable X. ii. The coefficient of determination is found by taking the square root of the coefficient of correlation.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.
iii. The standard error of estimate measures the accuracy of our prediction.
A) (i), (ii), and (iii) are all correct statements.
B) (i) and (ii) are correct statements but not (iii).
C) (i) and (iii) are correct statements but not (ii).
D) (ii) and (iii) are correct statements but not (i).
E) (i), (ii), and (iii) are all false statements.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 166 في هذه المجموعة.
فتح الحزمة
k this deck








