Deck 17: Regression Models With Dummy Variables
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/114
العب
ملء الشاشة (f)
Deck 17: Regression Models With Dummy Variables
1
Regression models that use a binary variable as the response variable are called binary choice models.
True
2
A dummy variable is commonly used to describe a quantitative variable with discrete or continuous values.
False
3
A binary choice model can be used,for example,to predict the chances of a candidate of winning an election.
True
4
For the model y = β0 + β1x + β2d + β3xd + ε,in which d is a dummy variable,we can perform standard t tests for the individual significance of x,d,and xd.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
5
Consider the regression model y = β0 + β1x + β2d + β3xd + ε.If the dummy variable d changes from 0 to 1,the estimated changes in the intercept and the slope are b0 + b2 and b2,respectively.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
6
A gender is an example of ______ variable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
7
The logistic model can be estimated through the use of the ordinary least squares method.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
8
A dummy variable is a variable that takes on the values of 0 and 1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
9
For the logistic model,the predicted values of the response variables can always be interpreted as probabilities.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
10
Using a ______ we can examine whether the particular dummy variable is statistically significant.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
11
For the linear probability model y = β0 + β1x + ε,the predictions made by 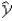 = b0 + b1x can be always interpreted as probabilities.
= b0 + b1x can be always interpreted as probabilities.
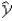 = b0 + b1x can be always interpreted as probabilities.
= b0 + b1x can be always interpreted as probabilities.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
12
If the number of dummy variables representing a qualitative variable equals the number of categories of this variable,one deals with the problem of perfect multicollinearity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
13
A dummy variable is also referred to as a(n)_________ variable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
14
In the regression equation 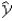 = b0 + b1x + b2d,a dummy variable d affects the slope of the line.
= b0 + b1x + b2d,a dummy variable d affects the slope of the line.
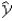 = b0 + b1x + b2d,a dummy variable d affects the slope of the line.
= b0 + b1x + b2d,a dummy variable d affects the slope of the line.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
15
For the model y = β0 + β1x + β2d + β3xd+ε,in which d is a dummy variable,we cannot perform the F test for the joint significance of the dummy variable d and the interaction variable xd.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
16
For the model y = β0 + β1x + β2d + β3xd + ε,the dummy variable d causes only a shift in intercept.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
17
A model y = β0 + β1x + ε,in which y is a binary variable,is called a linear probability model.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
18
If we include as many dummy variables as there are categories,then their sum will be equal to _____.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
19
The number of dummy variables representing a qualitative variable should be one less than the number of categories of the variable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
20
All variables employed in regression must be quantitative.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
21
In a model y = β0 + β1x + β2d + β3xd + ε,the ______ F test for the joint significance of d and xd can be performed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
22
Regression models that use a dummy variable as the response variable are called binary or discrete ______ models.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
23
A model formulated as y = β0 + β1x + ε = P(y = 1)+ ε is called a(n)______ probability model.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
24
A logit model ensures that the predicted probability of the binary response variable falls between _________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
25
A researcher has developed the following regression equation to predict the prices of luxurious Oceanside condominium units, 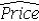 = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the difference in predicted prices of the ocean view and bay view units with the same square footage?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the difference in predicted prices of the ocean view and bay view units with the same square footage?
A) $40,000
B) $90,000
C) $500,000
D) $50,000
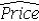 = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the difference in predicted prices of the ocean view and bay view units with the same square footage?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the difference in predicted prices of the ocean view and bay view units with the same square footage?A) $40,000
B) $90,000
C) $500,000
D) $50,000

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
26
For the model y = β0 + β1x + β2d + ε,which test is used for testing the significance of a dummy variable d?
A) F test
B) chi-square test
C) z test
D) t test
A) F test
B) chi-square test
C) z test
D) t test

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
27
Consider the model y = β0 + β1x + β2d + ε,where x is a quantitative variable and d is a dummy variable.For d = 1,the predicted value of y is computed as
A)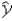 = b0 + b1x + b2x
= b0 + b1x + b2x
B)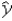 = b0 + b1x
= b0 + b1x
C) = (b0 +b1)x + b2
= (b0 +b1)x + b2
D)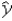
A)
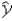 = b0 + b1x + b2x
= b0 + b1x + b2xB)
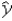 = b0 + b1x
= b0 + b1xC)
 = (b0 +b1)x + b2
= (b0 +b1)x + b2D)
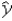

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
28
The maximum likelihood estimation (MLE)produces estimates for the ________ parameters β0 and β1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
29
Which of the following variables is not qualitative?
A) Gender of a person
B) Religious affiliation
C) Number of dependents claimed on a tax return
D) Student's status (freshman,sophomore,etc. )
A) Gender of a person
B) Religious affiliation
C) Number of dependents claimed on a tax return
D) Student's status (freshman,sophomore,etc. )

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
30
Consider the model y = β0 + β1x + β2d + ε,where x is a quantitative variable and d is a dummy variable.We can use sample data to estimate the model as _______________.
A)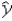 = b0+ b1x + b2d
= b0+ b1x + b2d
B)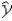 = b0 + b1x
= b0 + b1x
C) = b0 + b2d
= b0 + b2d
D)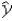
A)
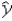 = b0+ b1x + b2d
= b0+ b1x + b2dB)
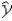 = b0 + b1x
= b0 + b1xC)
 = b0 + b2d
= b0 + b2dD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
31
Consider the regression equation 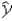 = b0 + b1x + b2d with a dummy variable d.If d increases from 0 to 1,the change in the intercept is given by:
= b0 + b1x + b2d with a dummy variable d.If d increases from 0 to 1,the change in the intercept is given by:
A) b0
B) b0 + b1
C) b2
D) b0 + b2
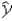 = b0 + b1x + b2d with a dummy variable d.If d increases from 0 to 1,the change in the intercept is given by:
= b0 + b1x + b2d with a dummy variable d.If d increases from 0 to 1,the change in the intercept is given by:A) b0
B) b0 + b1
C) b2
D) b0 + b2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
32
A researcher has developed the following regression equation to predict the prices of luxurious Oceanside condominium units, 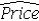 = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of a bay view unit measuring 1,500 square feet?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of a bay view unit measuring 1,500 square feet?
A) $315,000
B) $2,650,000
C) $265,000
D) $225,000
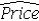 = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of a bay view unit measuring 1,500 square feet?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of a bay view unit measuring 1,500 square feet?A) $315,000
B) $2,650,000
C) $265,000
D) $225,000

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
33
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε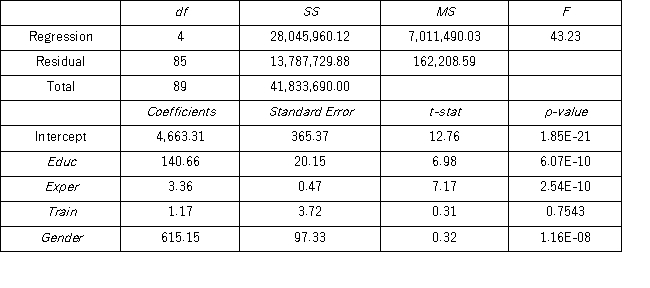 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Which of the following explanatory variables in Model A is most likely to be tested for the individual significance?
Which of the following explanatory variables in Model A is most likely to be tested for the individual significance?
A) Educ
B) Exper
C) Train
D) Gender
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Which of the following explanatory variables in Model A is most likely to be tested for the individual significance?
Which of the following explanatory variables in Model A is most likely to be tested for the individual significance?A) Educ
B) Exper
C) Train
D) Gender

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
34
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε 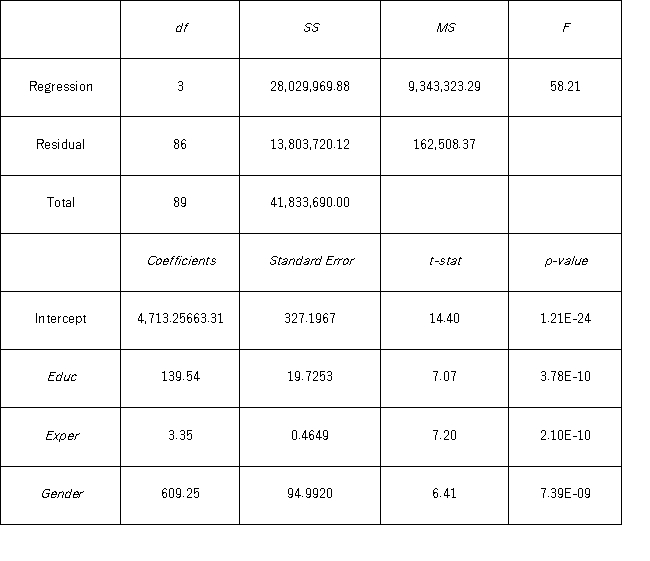 Which of the following is the regression equation found by Excel for Model A?
Which of the following is the regression equation found by Excel for Model A?
A)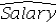 = 4663.31 + 140.66Educ + 3.36Exper + 1.17Train + 615.15Gender
= 4663.31 + 140.66Educ + 3.36Exper + 1.17Train + 615.15Gender
B)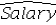 = 365.37 + 20.16Educ + 0.47Exper + 3.72Train + 97.33Gender
= 365.37 + 20.16Educ + 0.47Exper + 3.72Train + 97.33Gender
C)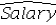 = 12.76 + 6.98Educ + 7.15Exper + 0.31Train + 6.32Gender
= 12.76 + 6.98Educ + 7.15Exper + 0.31Train + 6.32Gender
D)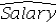
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Which of the following is the regression equation found by Excel for Model A?
Which of the following is the regression equation found by Excel for Model A?A)
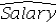 = 4663.31 + 140.66Educ + 3.36Exper + 1.17Train + 615.15Gender
= 4663.31 + 140.66Educ + 3.36Exper + 1.17Train + 615.15GenderB)
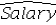 = 365.37 + 20.16Educ + 0.47Exper + 3.72Train + 97.33Gender
= 365.37 + 20.16Educ + 0.47Exper + 3.72Train + 97.33GenderC)
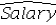 = 12.76 + 6.98Educ + 7.15Exper + 0.31Train + 6.32Gender
= 12.76 + 6.98Educ + 7.15Exper + 0.31Train + 6.32GenderD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
35
A dummy variable can be used to create a(n)_______ variable,which allows the estimated change in y to vary across the values of x.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
36
Quantitative variables assume meaningful ____,where as qualitative variables represent some ____.
A) categories,numeric values
B) numeric values,categories
C) categories,responses
D) responses,categories
A) categories,numeric values
B) numeric values,categories
C) categories,responses
D) responses,categories

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
37
To avoid the dummy variable _____,the number of dummy variables should be one less than the number of categories.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
38
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε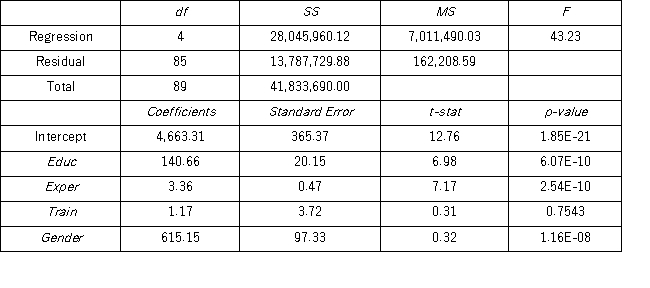 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Using Model A,which of the following is the estimated average difference between the salaries of male and female employees with the same years of education,months of experience,and weeks of training?
Using Model A,which of the following is the estimated average difference between the salaries of male and female employees with the same years of education,months of experience,and weeks of training?
A) About $5,423
B) About $619
C) About $5,278
D) About $615
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Using Model A,which of the following is the estimated average difference between the salaries of male and female employees with the same years of education,months of experience,and weeks of training?
Using Model A,which of the following is the estimated average difference between the salaries of male and female employees with the same years of education,months of experience,and weeks of training?A) About $5,423
B) About $619
C) About $5,278
D) About $615

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
39
A researcher has developed the following regression equation to predict the prices of luxurious Oceanside condominium units,  = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of an ocean view unit with 1,500 square feet?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of an ocean view unit with 1,500 square feet?
A) $315,000
B) $3,150,000
C) $265,000
D) $275,000
 = 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of an ocean view unit with 1,500 square feet?
= 40 + 0.15 Size + 50 View,where Price = the price of a unit (in $1,000s),Size = the square footage (in sq.feet),View = a dummy variable taking on 1 for an ocean view unit,and 0 for a bay view unit.Which of the following is the predicted price of an ocean view unit with 1,500 square feet?A) $315,000
B) $3,150,000
C) $265,000
D) $275,000

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
40
The logit model cannot be estimated with standard ______ least squares procedures.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
41
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε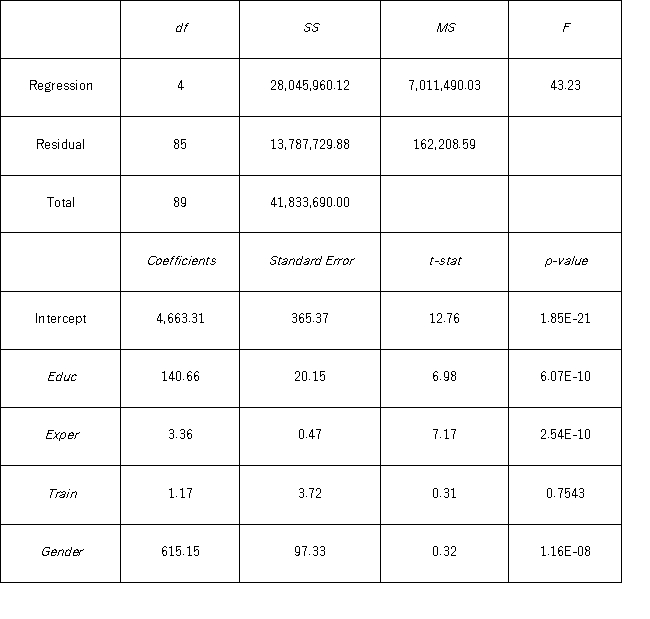 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Under the assumption of the same years of education and months of experience,what is the p-value for testing whether the mean salary of males is greater than the mean salary of females using Model B?
Under the assumption of the same years of education and months of experience,what is the p-value for testing whether the mean salary of males is greater than the mean salary of females using Model B?
A) At least 0.025
B) Less than 0.025 but at least 0.01
C) Less than 0.01 but at least 0.005
D) Less than 0.005
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Under the assumption of the same years of education and months of experience,what is the p-value for testing whether the mean salary of males is greater than the mean salary of females using Model B?
Under the assumption of the same years of education and months of experience,what is the p-value for testing whether the mean salary of males is greater than the mean salary of females using Model B?A) At least 0.025
B) Less than 0.025 but at least 0.01
C) Less than 0.01 but at least 0.005
D) Less than 0.005

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
42
For the model y = β0 + β1x + β2d1 + β3d2 + ε,which of the following tests is used for testing the joint significance of the dummy variables d1 and d2?
A) F test
B) t test
C) chi-square test
D) z test
A) F test
B) t test
C) chi-square test
D) z test

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
43
Consider the regression equation 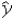 = b0 + b1xd with b1 > 0 and a dummy variable d.If d changes from 0 to 1,which of the following is true?
= b0 + b1xd with b1 > 0 and a dummy variable d.If d changes from 0 to 1,which of the following is true?
A) The intercept increases by b0 + b1.
B) The intercept increases by b1.
C) The slope increases by b0 + b1.
D) The slope increases by b1.
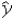 = b0 + b1xd with b1 > 0 and a dummy variable d.If d changes from 0 to 1,which of the following is true?
= b0 + b1xd with b1 > 0 and a dummy variable d.If d changes from 0 to 1,which of the following is true?A) The intercept increases by b0 + b1.
B) The intercept increases by b1.
C) The slope increases by b0 + b1.
D) The slope increases by b1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
44
Consider the following regression model, Humidity = β0 + β1 Temperature + β2 Spring + β3Summer + β4 Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.Assuming the same temperature and precipitation condition,what is the difference between the predicted humidity for summer and winter days?
A) b0 + b1 + b5
B) b0 + b3 + b5
C) b3
D) b0 + b5
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.Assuming the same temperature and precipitation condition,what is the difference between the predicted humidity for summer and winter days?
A) b0 + b1 + b5
B) b0 + b3 + b5
C) b3
D) b0 + b5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
45
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1Educ + β2Exper + β3Train + β4Gender + ε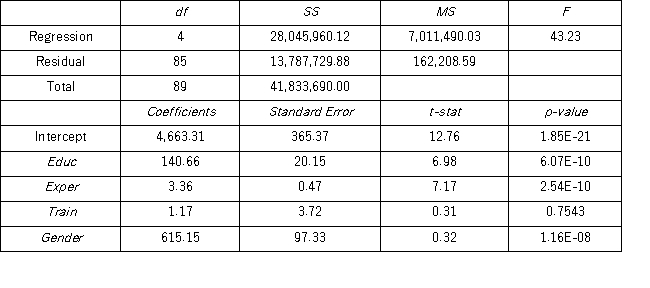 Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε
Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε 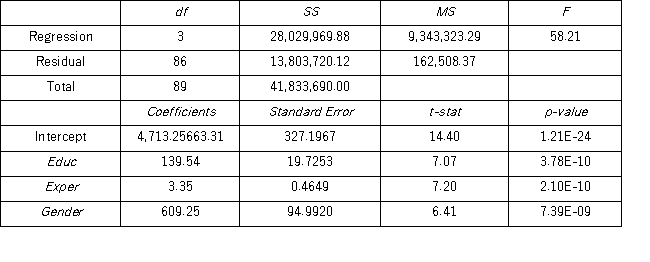 Using Model B,what is the regression equation found by Excel for males?
Using Model B,what is the regression equation found by Excel for males?
A)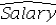 = 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
= 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
B) = 5,322.5011 + 139.5366Educ + 3.3488Exper
= 5,322.5011 + 139.5366Educ + 3.3488Exper
C) = 4,713.2506 + 139.5366Educ + 3.3488Exper
= 4,713.2506 + 139.5366Educ + 3.3488Exper
D)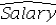
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1Educ + β2Exper + β3Train + β4Gender + ε
 Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε
Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε  Using Model B,what is the regression equation found by Excel for males?
Using Model B,what is the regression equation found by Excel for males?A)
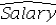 = 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
= 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505GenderB)
 = 5,322.5011 + 139.5366Educ + 3.3488Exper
= 5,322.5011 + 139.5366Educ + 3.3488ExperC)
 = 4,713.2506 + 139.5366Educ + 3.3488Exper
= 4,713.2506 + 139.5366Educ + 3.3488ExperD)
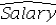

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
46
The model y = β0 + β1x + β2d + β3xd + ε is an example of a ______________________________________.
A) simple linear regression model
B) linear regression model with only dummy variable
C) linear regression model with dummy variable and quantitative variable
D) linear regression model with dummy variable,quantitative variable,and interaction variable
A) simple linear regression model
B) linear regression model with only dummy variable
C) linear regression model with dummy variable and quantitative variable
D) linear regression model with dummy variable,quantitative variable,and interaction variable

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
47
Consider the following regression model: Humidity = β0 + β1 Temperature + β2 Spring + β3Summer + β4 Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the winter rainy days?
A)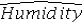 = (b0 + b3)+ b1Temperature + b5Rain
= (b0 + b3)+ b1Temperature + b5Rain
B)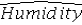 = (b0 + b5)+ b1Temperature
= (b0 + b5)+ b1Temperature
C)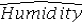 = (b0 + b2 + b3 + b4 + b5)+ b1Temperature
= (b0 + b2 + b3 + b4 + b5)+ b1Temperature
D)
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the winter rainy days?
A)
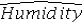 = (b0 + b3)+ b1Temperature + b5Rain
= (b0 + b3)+ b1Temperature + b5RainB)
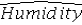 = (b0 + b5)+ b1Temperature
= (b0 + b5)+ b1TemperatureC)
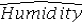 = (b0 + b2 + b3 + b4 + b5)+ b1Temperature
= (b0 + b2 + b3 + b4 + b5)+ b1TemperatureD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
48
Consider the following regression model: Humidity = β0 + β1 Temperature + β2 Spring + β3Summer + β4 Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the summer days?
A)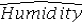 = (b0 + b3)+ b1Temperature + b5Rain
= (b0 + b3)+ b1Temperature + b5Rain
B)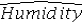 = b0 + b1Temperature + b5Rain
= b0 + b1Temperature + b5Rain
C) = b0 + b1Temperature + b2Spring + b5Rain
= b0 + b1Temperature + b2Spring + b5Rain
D)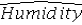
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the summer days?
A)
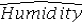 = (b0 + b3)+ b1Temperature + b5Rain
= (b0 + b3)+ b1Temperature + b5RainB)
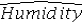 = b0 + b1Temperature + b5Rain
= b0 + b1Temperature + b5RainC)
 = b0 + b1Temperature + b2Spring + b5Rain
= b0 + b1Temperature + b2Spring + b5RainD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
49
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε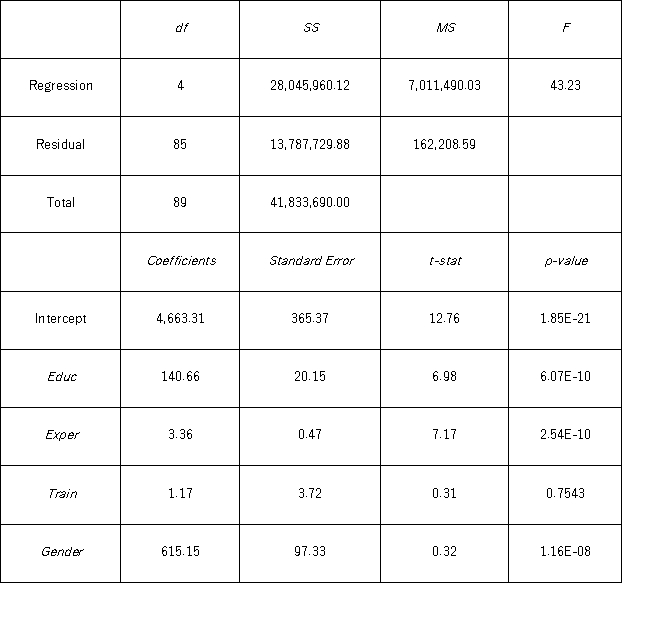 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε 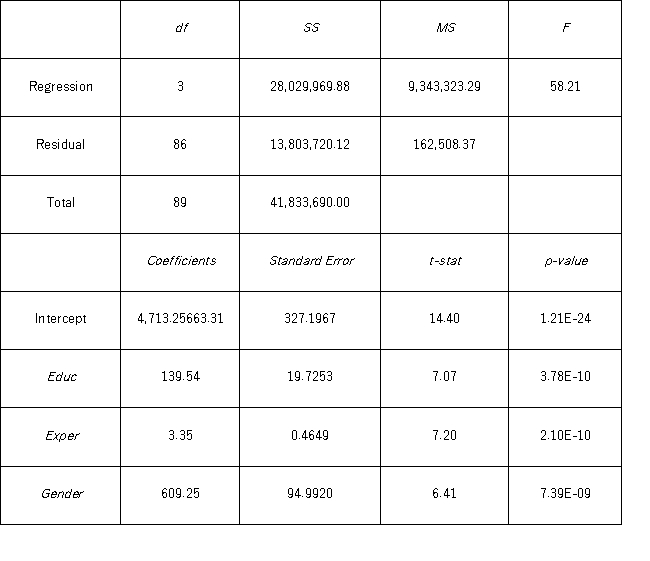 A group of female managers considers a discrimination lawsuit if on average their salaries can be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the alternative hypothesis for testing the lawsuit condition?
A group of female managers considers a discrimination lawsuit if on average their salaries can be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the alternative hypothesis for testing the lawsuit condition?
A) HA: β3 ≤ 500
B) HA: β3< 500
C) HA: β3 ≠ 500
D) HA: β3 > 500
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  A group of female managers considers a discrimination lawsuit if on average their salaries can be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the alternative hypothesis for testing the lawsuit condition?
A group of female managers considers a discrimination lawsuit if on average their salaries can be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the alternative hypothesis for testing the lawsuit condition?A) HA: β3 ≤ 500
B) HA: β3< 500
C) HA: β3 ≠ 500
D) HA: β3 > 500

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
50
Suppose that we have a qualitative variable Month with categories: January,February,etc.How many dummy variables are needed to describe Month?
A) 12
B) 11
C) 10
D) 9
A) 12
B) 11
C) 10
D) 9

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
51
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε 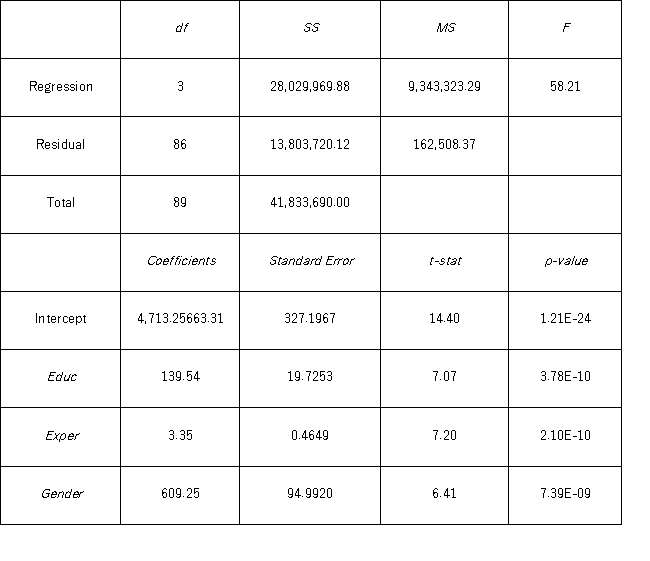 A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the conclusion of the appropriate test at 10% significance level?
A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the conclusion of the appropriate test at 10% significance level?
A) Do not reject H0;the salaries of female managers cannot be proven to be lower on average by more than $500.
B) Reject H0;the salaries of female managers cannot be proven to be lower on average by more than $500.
C) Do not reject H0;the salaries of female managers are lower on average by more than $500.
D) Reject H0;the salaries of female managers are lower on average by more than $500.
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the conclusion of the appropriate test at 10% significance level?
A group of female managers considers a discrimination lawsuit if on average their salaries could be statistically proven to be lower by more than $500 than the salaries of their male peers with the same level of education and experience.Using Model B,what is the conclusion of the appropriate test at 10% significance level?A) Do not reject H0;the salaries of female managers cannot be proven to be lower on average by more than $500.
B) Reject H0;the salaries of female managers cannot be proven to be lower on average by more than $500.
C) Do not reject H0;the salaries of female managers are lower on average by more than $500.
D) Reject H0;the salaries of female managers are lower on average by more than $500.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
52
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1Educ + β2Exper + β3Train + β4Gender + ε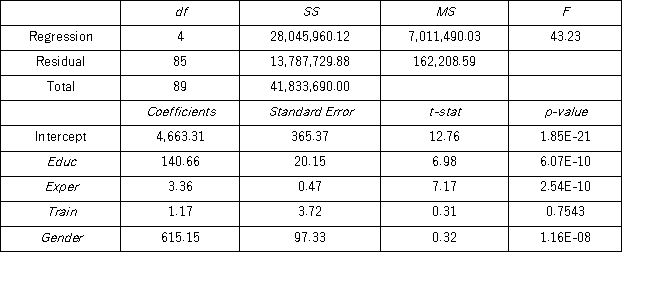 Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε
Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε 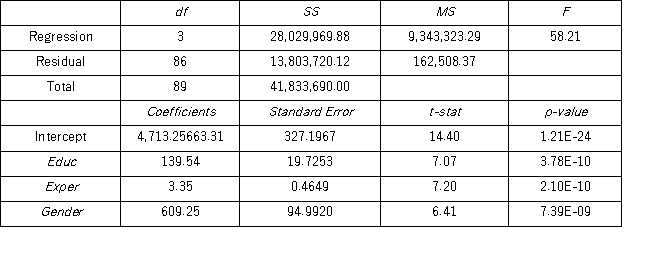 Using Model B,what is the regression equation found by Excel for females?
Using Model B,what is the regression equation found by Excel for females?
A) = 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
= 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
B)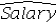 = 5,322.5011 + 139.5366Educ + 3.3488Exper
= 5,322.5011 + 139.5366Educ + 3.3488Exper
C)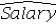 = 4,713.2506 + 139.5366Educ + 3.3488Exper
= 4,713.2506 + 139.5366Educ + 3.3488Exper
D)
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1Educ + β2Exper + β3Train + β4Gender + ε
 Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε
Model B: Salary = β0 + β1Educ + β2Exper + β3Gender + ε  Using Model B,what is the regression equation found by Excel for females?
Using Model B,what is the regression equation found by Excel for females?A)
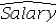 = 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505Gender
= 4,713.2506 + 139.5366Educ + 3.3488Exper + 609.2505GenderB)
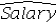 = 5,322.5011 + 139.5366Educ + 3.3488Exper
= 5,322.5011 + 139.5366Educ + 3.3488ExperC)
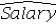 = 4,713.2506 + 139.5366Educ + 3.3488Exper
= 4,713.2506 + 139.5366Educ + 3.3488ExperD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
53
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε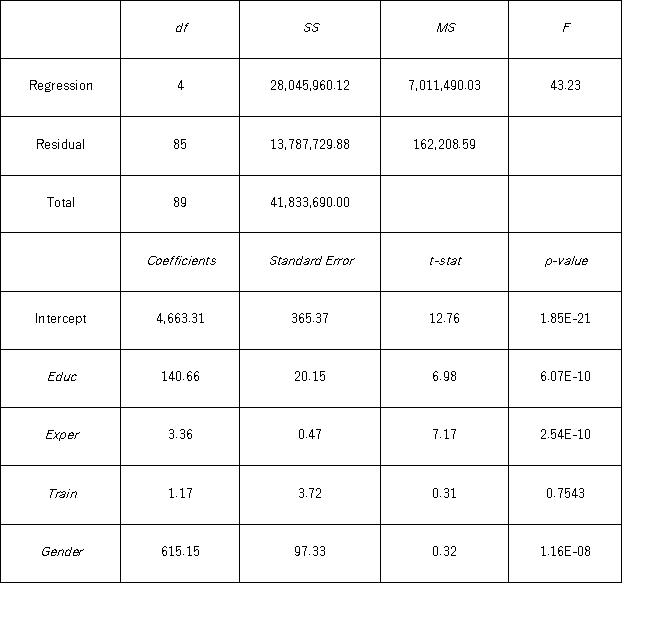 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε 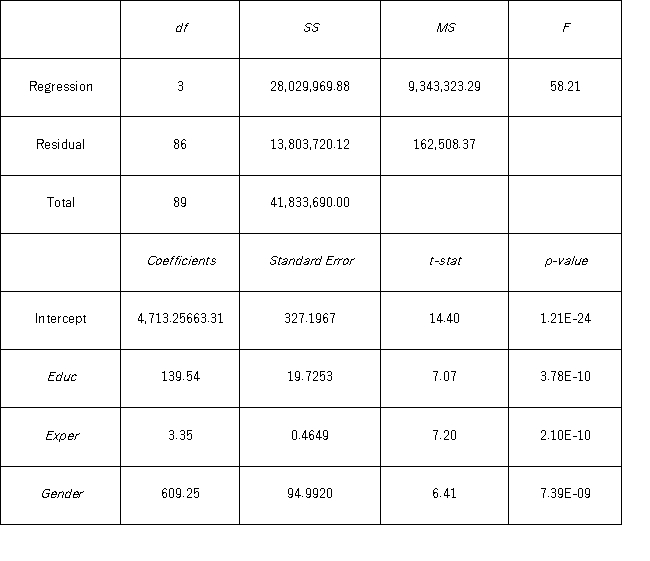 Under the assumption of the same years of education and months of experience,what is the null hypothesis for testing whether the mean salary of males is greater than the mean salary of females using Model B?
Under the assumption of the same years of education and months of experience,what is the null hypothesis for testing whether the mean salary of males is greater than the mean salary of females using Model B?
A) H0: β3 ≤ 0
B) H0: β3 ≥ 0
C) H0: β3> 0
D) H0: β3 = 0
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  Under the assumption of the same years of education and months of experience,what is the null hypothesis for testing whether the mean salary of males is greater than the mean salary of females using Model B?
Under the assumption of the same years of education and months of experience,what is the null hypothesis for testing whether the mean salary of males is greater than the mean salary of females using Model B?A) H0: β3 ≤ 0
B) H0: β3 ≥ 0
C) H0: β3> 0
D) H0: β3 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
54
Consider the following regression model: Humidity = β0 + β1 Temperature + β2 Spring + β3 Summer + β4Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the winter days?
A) = (b0 + b3)+b1Temperature + b5Rain
= (b0 + b3)+b1Temperature + b5Rain
B)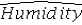 = (b0 + b2 + b3 + b4)+ b1Temperature + b5Rain
= (b0 + b2 + b3 + b4)+ b1Temperature + b5Rain
C)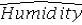 = b0 + b1Temperature + b5Rain
= b0 + b1Temperature + b5Rain
D)
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the winter days?
A)
 = (b0 + b3)+b1Temperature + b5Rain
= (b0 + b3)+b1Temperature + b5RainB)
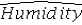 = (b0 + b2 + b3 + b4)+ b1Temperature + b5Rain
= (b0 + b2 + b3 + b4)+ b1Temperature + b5RainC)
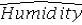 = b0 + b1Temperature + b5Rain
= b0 + b1Temperature + b5RainD)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
55
Which of the following regression models does not include an interaction variable?
A) y = β0 + β1x + β2xd + ε
B) y = β0 + β1x + β2x2 + ε
C) y = β0 + β1d + β2xd + ε
D) y = β0 + β1x + β2d + β3xd + ε
A) y = β0 + β1x + β2xd + ε
B) y = β0 + β1x + β2x2 + ε
C) y = β0 + β1d + β2xd + ε
D) y = β0 + β1x + β2d + β3xd + ε

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
56
Consider the following regression model: Humidity = β0 + β1 Temperature + β2 Spring + β3Summer + β4 Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.Assuming the same temperature and precipitation condition,what is the difference between the predicted humidity for summer and fall days?
A) b0 + b3 - b4
B) b3 - b4
C) b3 + b4
D) b0 + b4 - b3
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.Assuming the same temperature and precipitation condition,what is the difference between the predicted humidity for summer and fall days?
A) b0 + b3 - b4
B) b3 - b4
C) b3 + b4
D) b0 + b4 - b3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
57
In the model y = β0 + β1x + β2d + β3xd + ε,the dummy variable and the interaction variable cause ____________________________________.
A) a change in just the intercept
B) a change in just the slope
C) a change in both the intercept as well as the slope
D) None of these choices is correct.
A) a change in just the intercept
B) a change in just the slope
C) a change in both the intercept as well as the slope
D) None of these choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
58
The number of dummy variables representing a qualitative variable should be ____________________________.
A) one less than the number of categories of the variable
B) two less than the number of categories of the variable
C) the same number as the number of categories of the variable
D) None of these choices is correct.
A) one less than the number of categories of the variable
B) two less than the number of categories of the variable
C) the same number as the number of categories of the variable
D) None of these choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
59
To examine the differences between salaries of male and female middle managers of a large bank,90 individuals were randomly selected,and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses),
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε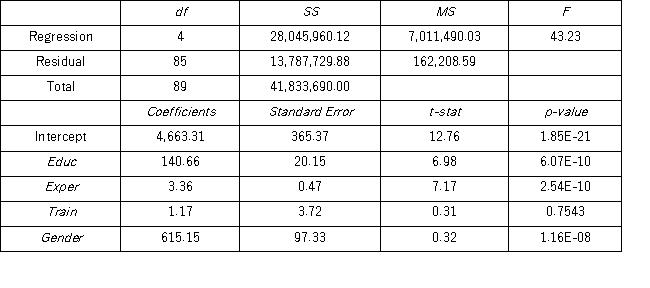 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε 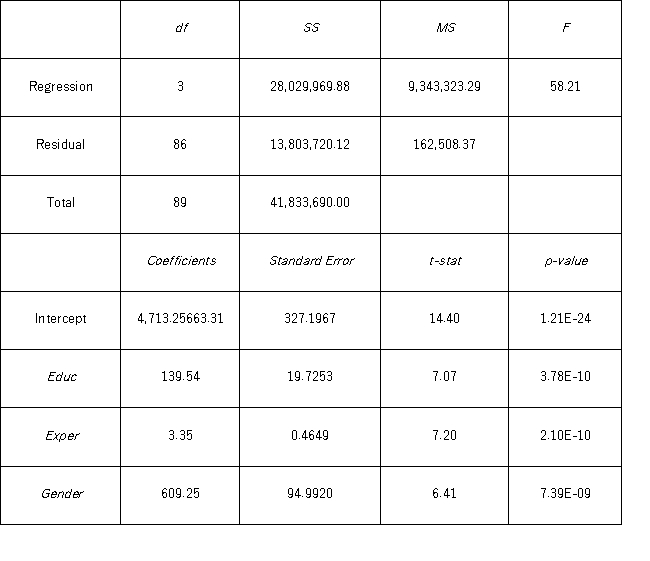 When testing the individual significance of Train in Model A,what is the test conclusion at 10% significance level?
When testing the individual significance of Train in Model A,what is the test conclusion at 10% significance level?
A) Do not reject H0;Train is significant.
B) Reject H0;Train is significant.
C) Reject H0;Train does not seem to be significant.
D) Do not reject H0;Train does not seem to be significant.
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual;1 for males,and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β0 + β1 Educ + β2 Exper + β3 Train + β4 Gender + ε
 Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε
Model B: Salary = β0 + β1 Educ + β2 Exper + β3 Gender + ε  When testing the individual significance of Train in Model A,what is the test conclusion at 10% significance level?
When testing the individual significance of Train in Model A,what is the test conclusion at 10% significance level?A) Do not reject H0;Train is significant.
B) Reject H0;Train is significant.
C) Reject H0;Train does not seem to be significant.
D) Do not reject H0;Train does not seem to be significant.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
60
Consider the following regression model: Humidity = β0 + β1 Temperature + β2 Spring + β3 Summer + β4 Fall + β5 Rain + ε,
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the summer rainy days?
A) = (b0 + b3)+ b1Temperature
= (b0 + b3)+ b1Temperature
B) = (b0 + b5)+ b1Temperature
= (b0 + b5)+ b1Temperature
C) = b0 + b1Temperature + b2Spring + b4Fall
= b0 + b1Temperature + b2Spring + b4Fall
D)
Where the dummy variables Spring,Summer,and Fall represent the qualitative variable Season (spring,summer,fall,winter),and the dummy variable Rain is defined as Rain = 1 if rainy day,Rain = 0 otherwise.What is the regression equation for the summer rainy days?
A)
 = (b0 + b3)+ b1Temperature
= (b0 + b3)+ b1TemperatureB)
 = (b0 + b5)+ b1Temperature
= (b0 + b5)+ b1TemperatureC)
 = b0 + b1Temperature + b2Spring + b4Fall
= b0 + b1Temperature + b2Spring + b4FallD)


فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
61
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.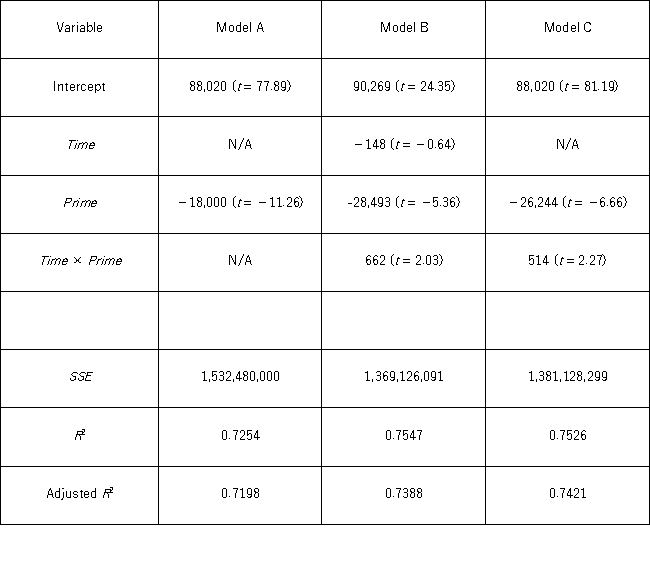 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Which of the following three models would you choose to make the predictions of the remaining loan balance?
A) Model A
B) Model B
C) Model C
D) Any model
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Which of the following three models would you choose to make the predictions of the remaining loan balance?
A) Model A
B) Model B
C) Model C
D) Any model

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
62
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.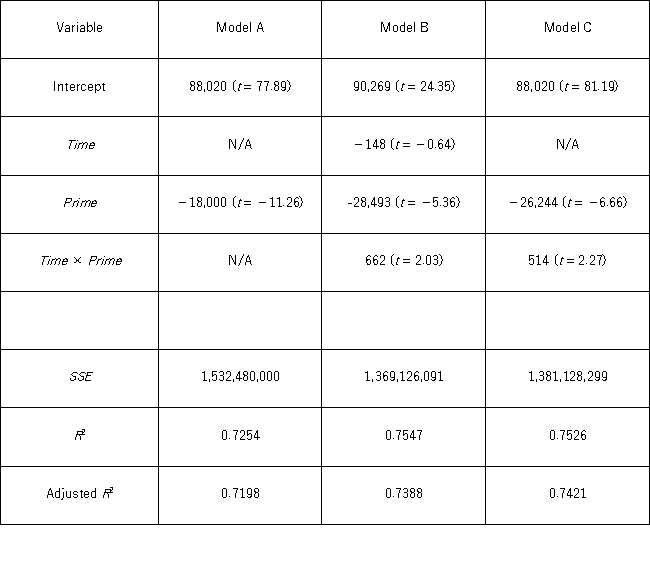 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Using Model B,what is the value of the test statistic for testing the joint significance of the variable Time and the interaction variable Time × Prime?
A) −0.64
B) −5.36
C) 2.03
D) 2.74
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Using Model B,what is the value of the test statistic for testing the joint significance of the variable Time and the interaction variable Time × Prime?
A) −0.64
B) −5.36
C) 2.03
D) 2.74

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
63
Which of the following predictions cannot be described by a binary choice model?
A) Predict the ability to swim through the English Channel.
B) Predict the chances of a candidate winning the next presidential election.
C) Predict today's number of cars crossing the Golden Gate Bridge.
D) Predict the occurrence of a hurricane in Florida next year.
A) Predict the ability to swim through the English Channel.
B) Predict the chances of a candidate winning the next presidential election.
C) Predict today's number of cars crossing the Golden Gate Bridge.
D) Predict the occurrence of a hurricane in Florida next year.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
64
In the model y = β0 + β1x + β2d + β3xd + ε,for a given x and d = 1,the predicted value of y is given by _________________________.
A)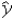 = b0 + b1x + b2 + b3x
= b0 + b1x + b2 + b3x
B)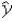 = b0 + b2 + b1x + b3x
= b0 + b2 + b1x + b3x
C)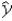 = (b0 + b2)+ (b1 + b3)x
= (b0 + b2)+ (b1 + b3)x
D) All of these choices are correct.
A)
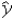 = b0 + b1x + b2 + b3x
= b0 + b1x + b2 + b3xB)
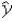 = b0 + b2 + b1x + b3x
= b0 + b2 + b1x + b3xC)
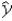 = (b0 + b2)+ (b1 + b3)x
= (b0 + b2)+ (b1 + b3)xD) All of these choices are correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
65
For the model y = β0 + β1x + β2xd + ε,which of the following are the hypotheses for testing the individual significance of the interaction variable xd?
A) H0: xd = 0,HA: xd ≠ 0
B) H0: b2 = 0,HA: b2 ≠ 0
C) H0: β2 = 0,HA: β2 ≠ 0
D) H0: β2 ≠ 0,HA: β2 = 0
A) H0: xd = 0,HA: xd ≠ 0
B) H0: b2 = 0,HA: b2 ≠ 0
C) H0: β2 = 0,HA: β2 ≠ 0
D) H0: β2 ≠ 0,HA: β2 = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
66
In the model y = β0 + β1x + β2d + β3xd + ε,when d changes from 0 to 1 how does the intercept of the corresponding lines change?
A) From b0 to b0 + b1
B) From b0 to b0 + b2
C) From b0 to b0 + b3
D) From b0 to b0 + b1 + b2
A) From b0 to b0 + b1
B) From b0 to b0 + b2
C) From b0 to b0 + b3
D) From b0 to b0 + b1 + b2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
67
The major shortcoming of the general linear probability model y = β0 + β1x1 + β2x2 + … + βkxk+ ε,is that the predicted values of y can be sometimes _______________________.
A) greater than 0 and less than 1
B) at least 0 and no more than 1
C) less than 1 but more than 0
D) less than 0 or greater than 1
A) greater than 0 and less than 1
B) at least 0 and no more than 1
C) less than 1 but more than 0
D) less than 0 or greater than 1

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
68
A logistic model can be estimated with the method of _____________________.
A) ordinary least squares
B) maximum likelihood estimation
C) ANOVA
D) nonparametric estimation
A) ordinary least squares
B) maximum likelihood estimation
C) ANOVA
D) nonparametric estimation

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
69
In the regression equation  = b0 + b1x + b2dx with a dummy variable d,when d changes from 0 to 1,the change in the slope of the corresponding lines is given by ______.
= b0 + b1x + b2dx with a dummy variable d,when d changes from 0 to 1,the change in the slope of the corresponding lines is given by ______.
A) b0
B) b0 + b1
C) b2
D) b0 + b2
 = b0 + b1x + b2dx with a dummy variable d,when d changes from 0 to 1,the change in the slope of the corresponding lines is given by ______.
= b0 + b1x + b2dx with a dummy variable d,when d changes from 0 to 1,the change in the slope of the corresponding lines is given by ______.A) b0
B) b0 + b1
C) b2
D) b0 + b2

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
70
Which of the following is an estimated logistic model?
A)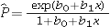
B)
C)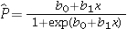
D)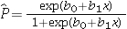
A)
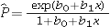
B)

C)
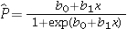
D)
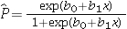

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
71
For the linear probability model y = β0 + β1x + ε,the predicted value of y is always constrained between ________.
A) 0 and 1.
B) −1 and 1.
C) Both 0 and 1,and −1 and 1 are correct.
D) None of these choices is correct.
A) 0 and 1.
B) −1 and 1.
C) Both 0 and 1,and −1 and 1 are correct.
D) None of these choices is correct.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
72
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.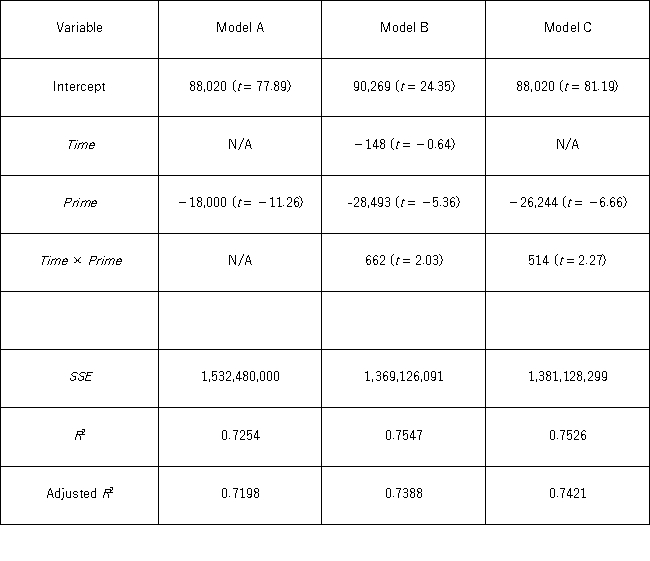 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Using Model B,what is the null hypothesis for testing the joint significance of the variable Time and the interaction variable Time × Prime?
A) H0: β1 = β2 = β3 = 0
B) H0: β1 = 0 and β3 = 0
C) H0: β1 = 0 or β3 = 0
D) H0: β1 ≠ 0 or β3 ≠ 0
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Using Model B,what is the null hypothesis for testing the joint significance of the variable Time and the interaction variable Time × Prime?
A) H0: β1 = β2 = β3 = 0
B) H0: β1 = 0 and β3 = 0
C) H0: β1 = 0 or β3 = 0
D) H0: β1 ≠ 0 or β3 ≠ 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
73
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.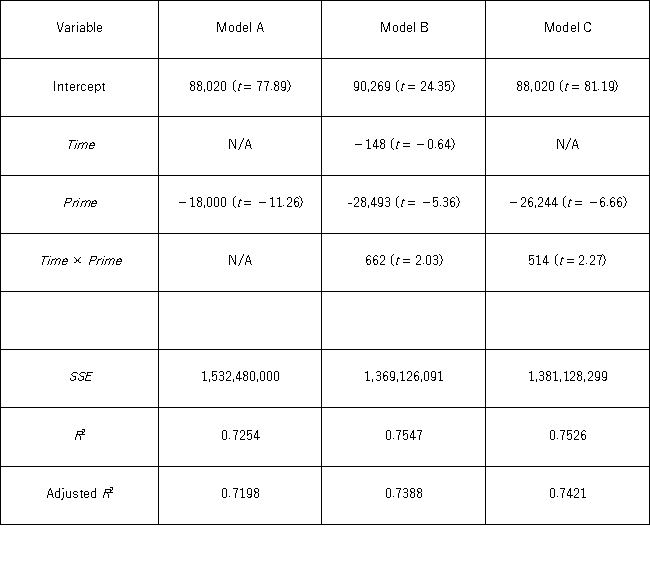 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Using Model B,what is the conclusion for testing the joint significance of the variable Time and the interaction variable Time × Prime at 5% significance level?
A) Reject H0;Time and Time × Prime are jointly significant.
B) Do not reject H0;Time and Time × Prime are jointly significant.
C) Reject H0;Time and Time × Prime cannot be proven to be jointly insignificant.
D) Do not reject H0;Time and Time × Prime cannot be proven to be jointly significant.
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Using Model B,what is the conclusion for testing the joint significance of the variable Time and the interaction variable Time × Prime at 5% significance level?
A) Reject H0;Time and Time × Prime are jointly significant.
B) Do not reject H0;Time and Time × Prime are jointly significant.
C) Reject H0;Time and Time × Prime cannot be proven to be jointly insignificant.
D) Do not reject H0;Time and Time × Prime cannot be proven to be jointly significant.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
74
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.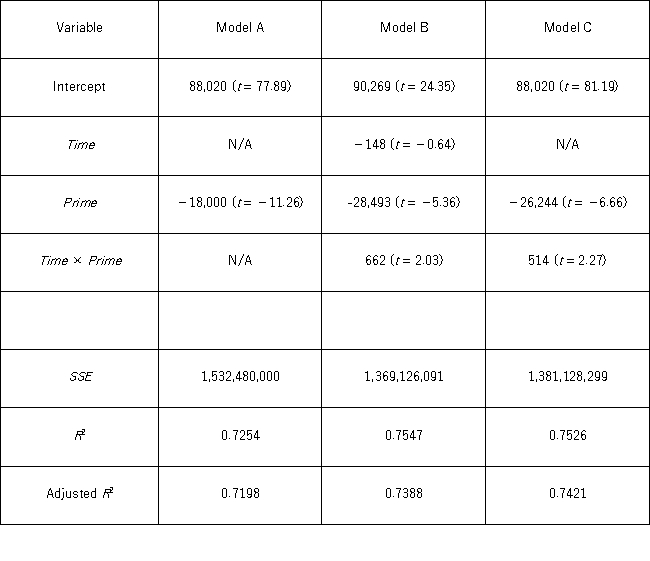 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Using Model C,which of the following is the predicted balance on a $100,000 prime loan taken 15 years ago?
A) $88,020
B) $69,486
C) $74,591
D) $82,183
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Using Model C,which of the following is the predicted balance on a $100,000 prime loan taken 15 years ago?
A) $88,020
B) $69,486
C) $74,591
D) $82,183

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
75
The major advantage of a logistic model over the corresponding linear probability model is that the predicted values of y are always between _________.
A) −1 and 1
B) 0 and 2
C) 0 and 1
D) −1 and 0
A) −1 and 1
B) 0 and 2
C) 0 and 1
D) −1 and 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
76
Which of the following predictions can be described by a binary choice model?
A) Predict the day's temperature in degrees Fahrenheit.
B) Predict whether a student will pass or fail a test.
C) Predict today's price of gasoline per gallon in dollars.
D) Predict the rainfall in millimeters today.
A) Predict the day's temperature in degrees Fahrenheit.
B) Predict whether a student will pass or fail a test.
C) Predict today's price of gasoline per gallon in dollars.
D) Predict the rainfall in millimeters today.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
77
Which of the following represents a logistic regression model?
A) P = β0 + β1x
B)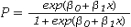
C) P = β0 + β1 ln(x)
D) P = exp(β0 + β1x)
A) P = β0 + β1x
B)
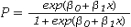
C) P = β0 + β1 ln(x)
D) P = exp(β0 + β1x)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
78
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.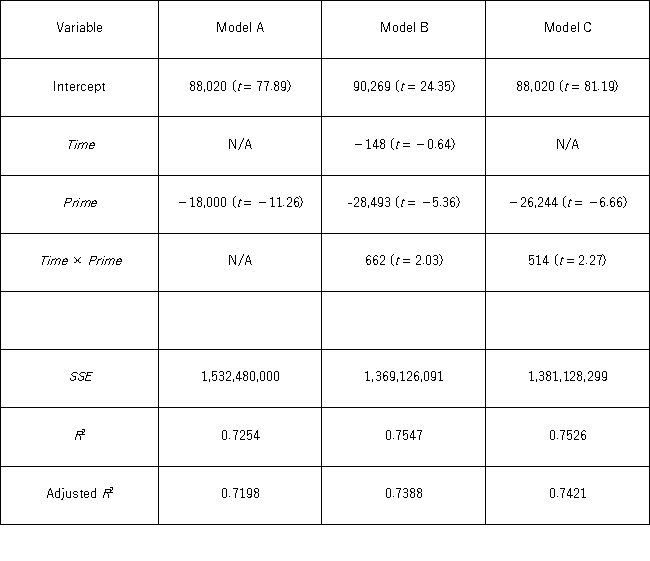 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Using Model B,which of the following is the alternative hypothesis for testing the significance of Time?
A) HA: β1 = 0
B) HA: β1 = 0 and β3 = 0
C) HA: β1 ≠ 0
D) HA: β1 ≠ 0 or β3 ≠ 0
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Using Model B,which of the following is the alternative hypothesis for testing the significance of Time?
A) HA: β1 = 0
B) HA: β1 = 0 and β3 = 0
C) HA: β1 ≠ 0
D) HA: β1 ≠ 0 or β3 ≠ 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
79
For a linear regression model with a dummy variable d and an interaction variable xd,we _______________________________________________________________.
A) cannot conduct the F test for the joint significance of d and xd
B) can conduct the F test for the joint significance of d and xd
C) cannot conduct t test for the individual significance of d and xd
D) can conduct the chi-square test for testing the independence of attributes
A) cannot conduct the F test for the joint significance of d and xd
B) can conduct the F test for the joint significance of d and xd
C) cannot conduct t test for the individual significance of d and xd
D) can conduct the chi-square test for testing the independence of attributes

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck
80
A researcher wants to examine how the remaining balance on $100,000 loans taken 10 to 20 years ago depends on whether the loan was a prime or subprime loan.He collected a sample of 25 prime loans and 25 subprime loans and recorded the data in the following variables: Balance = the remaining amount of loan to be paid off (in $),
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.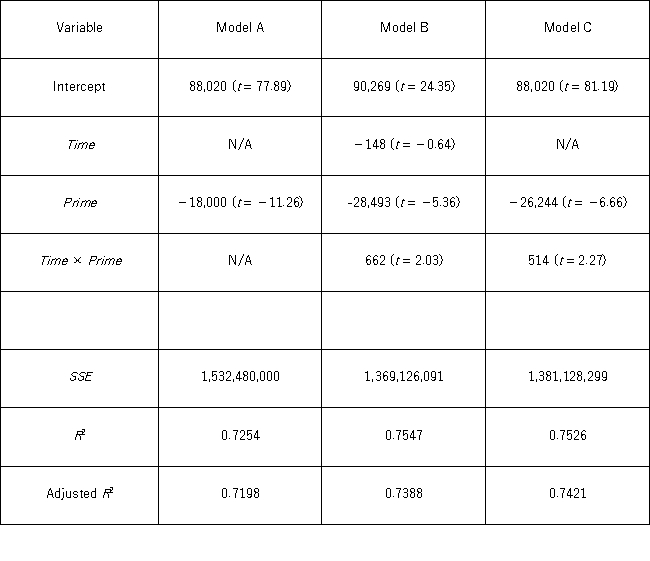 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Which of the following is the p-value for testing the individual significance of Time in Model B?
A) Less than 0.10
B) Less than 0.20 but at least 0.10
C) Less than 0.40 but at least 0.20
D) More than 0.40
Time = the time elapsed from taking the loan,
Prime = a dummy variable assuming 1 for prime loans,and 0 for subprime loans.
The regression results obtained for the models:
Model A: Balance = β0 + β1Prime + ε
Model B: Balance = β0 + β1Time + β2Prime + β3Time × Prime + ε
Model C: Balance = β0 + β1Prime + β2Time × Prime + ε,
Are summarized in the following table.
 Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.
Note: The values of relevant test statistics are shown in parentheses below the estimated coefficients.Which of the following is the p-value for testing the individual significance of Time in Model B?
A) Less than 0.10
B) Less than 0.20 but at least 0.10
C) Less than 0.40 but at least 0.20
D) More than 0.40

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 114 في هذه المجموعة.
فتح الحزمة
k this deck








