Deck 12: Instrumental Variables Regression
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/50
العب
ملء الشاشة (f)
Deck 12: Instrumental Variables Regression
1
When calculating the TSLS standard errors
A)you do not have to worry about heteroskedasticity,since it was eliminated in the first stage
B)you can use the standard errors reported by OLS estimation of the second stage regression.
C)the critical values from the standard normal table should be adjusted for the proper degrees of freedom.
D)you should use heteroskedasticity-robust standard errors.
A)you do not have to worry about heteroskedasticity,since it was eliminated in the first stage
B)you can use the standard errors reported by OLS estimation of the second stage regression.
C)the critical values from the standard normal table should be adjusted for the proper degrees of freedom.
D)you should use heteroskedasticity-robust standard errors.
D
2
(Requires Appendix material)The relationship between the TSLS slope and the corresponding population parameter is:
A) .
.
B) .
.
C)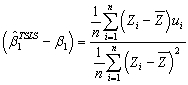 .
.
D)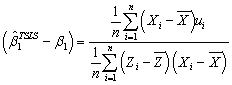 .
.
A)
 .
.B)
 .
.C)
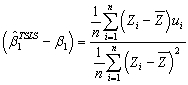 .
.D)
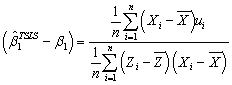 .
.A
3
Instrument relevance
A)means that the instrument is one of the determinants of the dependent variable.
B)is the same as instrument exogeneity.
C)means that some of the variance in the regressor is related to variation in the instrument.
D)is not possible since X and u are correlated and Z and u are not correlated.
A)means that the instrument is one of the determinants of the dependent variable.
B)is the same as instrument exogeneity.
C)means that some of the variance in the regressor is related to variation in the instrument.
D)is not possible since X and u are correlated and Z and u are not correlated.
C
4
The distinction between endogenous and exogenous variables is
A)that exogenous variables are determined inside the model and endogenous variables are determined outside the model.
B)dependent on the sample size: for n > 100,endogenous variables become exogenous.
C)depends on the distribution of the variables: when they are normally distributed,they are exogenous,otherwise they are endogenous.
D)whether or not the variables are correlated with the error term.
A)that exogenous variables are determined inside the model and endogenous variables are determined outside the model.
B)dependent on the sample size: for n > 100,endogenous variables become exogenous.
C)depends on the distribution of the variables: when they are normally distributed,they are exogenous,otherwise they are endogenous.
D)whether or not the variables are correlated with the error term.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
5
Two Stage Least Squares is calculated as follows;in the first stage:
A)Y is regressed on the exogenous variables only.The predicted value of Y is then regressed on the instrumental variables.
B)the unknown coefficients in the reduced form equation are estimated by OLS,and the predicted values are calculated.In the second stage,Y is regressed on these predicted values and the other exogenous variables.
C)the exogenous variables are regressed on the instruments.The predicted value of the exogenous variables is then used in the second stage,together with the instruments,to predict the dependent variable.
D)the unknown coefficients in the reduced form equation are estimated by weighted least squares,and the predicted values are calculated.In the second stage,Y is regressed on these predicted values and the other exogenous variables.
A)Y is regressed on the exogenous variables only.The predicted value of Y is then regressed on the instrumental variables.
B)the unknown coefficients in the reduced form equation are estimated by OLS,and the predicted values are calculated.In the second stage,Y is regressed on these predicted values and the other exogenous variables.
C)the exogenous variables are regressed on the instruments.The predicted value of the exogenous variables is then used in the second stage,together with the instruments,to predict the dependent variable.
D)the unknown coefficients in the reduced form equation are estimated by weighted least squares,and the predicted values are calculated.In the second stage,Y is regressed on these predicted values and the other exogenous variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
6
In the case of the simple regression model Yi = β0 + β1Xi + ui,i = 1,…,n,when X and u are correlated,then
A)the OLS estimator is biased in small samples only.
B)OLS and TSLS produce the same estimate.
C)X is exogenous.
D)the OLS estimator is inconsistent.
A)the OLS estimator is biased in small samples only.
B)OLS and TSLS produce the same estimate.
C)X is exogenous.
D)the OLS estimator is inconsistent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
7
The two conditions for a valid instrument are
A)corr(Zi,Xi)= 0 and corr(Zi,ui)≠ 0.
B)corr(Zi,Xi)= 0 and corr(Zi,ui)= 0.
C)corr(Zi,Xi)≠ 0 and corr(Zi,ui)= 0.
D)corr(Zi,Xi)≠ 0 and corr(Zi,ui)≠ 0.
A)corr(Zi,Xi)= 0 and corr(Zi,ui)≠ 0.
B)corr(Zi,Xi)= 0 and corr(Zi,ui)= 0.
C)corr(Zi,Xi)≠ 0 and corr(Zi,ui)= 0.
D)corr(Zi,Xi)≠ 0 and corr(Zi,ui)≠ 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
8
The conditions for a valid instruments do not include the following:
A)each instrument must be uncorrelated with the error term.
B)each one of the instrumental variables must be normally distributed.
C)at least one of the instruments must enter the population regression of X on the Zs and the Ws.
D)perfect multicollinearity between the predicted endogenous variables and the exogenous variables must be ruled out.
A)each instrument must be uncorrelated with the error term.
B)each one of the instrumental variables must be normally distributed.
C)at least one of the instruments must enter the population regression of X on the Zs and the Ws.
D)perfect multicollinearity between the predicted endogenous variables and the exogenous variables must be ruled out.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
9
The IV regression assumptions include all of the following with the exception of
A)the error terms must be normally distributed.
B)E(ui W1i,…,Wri)= 0.
W1i,…,Wri)= 0.
C)Large outliers are unlikely: the X's,W's,Z's,and Y's all have nonzero,finite fourth moments.
D)(X1i,…,Xki,W1i,…,Wri,Z1i,… Zmi,Yi)are i.i.d.draws from their joint distribution.
A)the error terms must be normally distributed.
B)E(ui
 W1i,…,Wri)= 0.
W1i,…,Wri)= 0.C)Large outliers are unlikely: the X's,W's,Z's,and Y's all have nonzero,finite fourth moments.
D)(X1i,…,Xki,W1i,…,Wri,Z1i,… Zmi,Yi)are i.i.d.draws from their joint distribution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
10
The following will not cause correlation between X and u in the simple regression model:
A)simultaneous causality.
B)omitted variables.
C)irrelevance of the regressor.
D)errors in variables.
A)simultaneous causality.
B)omitted variables.
C)irrelevance of the regressor.
D)errors in variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
11
When there is a single instrument and single regressor,the TSLS estimator for the slope can be calculated as follows:
A) .
.
B)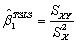 .
.
C) .
.
D)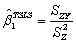 .
.
A)
 .
.B)
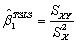 .
.C)
 .
.D)
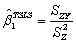 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
12
If the instruments are not exogenous,
A)you cannot perform the first stage of TSLS.
B)then,in order to conduct proper inference,it is essential that you use heteroskedasticity-robust standard errors.
C)your model becomes overidentified.
D)then TSLS is inconsistent.
A)you cannot perform the first stage of TSLS.
B)then,in order to conduct proper inference,it is essential that you use heteroskedasticity-robust standard errors.
C)your model becomes overidentified.
D)then TSLS is inconsistent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
13
The J-statistic
A)tells you if the instruments are exogenous.
B)provides you with a test of the hypothesis that the instruments are exogenous for the case of exact identification.
C)is distributed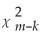 where m-k is the degree of overidentification.
where m-k is the degree of overidentification.
D)is distributed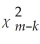 where m-k is the number of instruments minus the number of regressors.
where m-k is the number of instruments minus the number of regressors.
A)tells you if the instruments are exogenous.
B)provides you with a test of the hypothesis that the instruments are exogenous for the case of exact identification.
C)is distributed
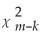 where m-k is the degree of overidentification.
where m-k is the degree of overidentification.D)is distributed
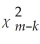 where m-k is the number of instruments minus the number of regressors.
where m-k is the number of instruments minus the number of regressors.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
14
Having more relevant instruments
A)is a problem because instead of being just identified,the regression now becomes overidentified.
B)is like having a larger sample size in that the more information is available for use in the IV regressions.
C)typically results in larger standard errors for the TSLS estimator.
D)is not as important for inference as having the same number of endogenous variables as instruments.
A)is a problem because instead of being just identified,the regression now becomes overidentified.
B)is like having a larger sample size in that the more information is available for use in the IV regressions.
C)typically results in larger standard errors for the TSLS estimator.
D)is not as important for inference as having the same number of endogenous variables as instruments.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
15
Consider a competitive market where the demand and the supply depend on the current price of the good.Then fitting a line through the quantity-price outcomes will
A)give you an estimate of the demand curve.
B)estimate neither a demand curve nor a supply curve.
C)enable you to calculate the price elasticity of supply.
D)give you the exogenous part of the demand in the first stage of TSLS.
A)give you an estimate of the demand curve.
B)estimate neither a demand curve nor a supply curve.
C)enable you to calculate the price elasticity of supply.
D)give you the exogenous part of the demand in the first stage of TSLS.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
16
Weak instruments are a problem because
A)the TSLS estimator may not be normally distributed,even in large samples.
B)they result in the instruments not being exogenous.
C)the TSLS estimator cannot be computed.
D)you cannot predict the endogenous variables any longer in the first stage.
A)the TSLS estimator may not be normally distributed,even in large samples.
B)they result in the instruments not being exogenous.
C)the TSLS estimator cannot be computed.
D)you cannot predict the endogenous variables any longer in the first stage.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
17
Estimation of the IV regression model
A)requires exact identification.
B)allows only one endogenous regressor,which is typically correlated with the error term.
C)requires exact identification or overidentification.
D)is only possible if the number of instruments is the same as the number of regressors.
A)requires exact identification.
B)allows only one endogenous regressor,which is typically correlated with the error term.
C)requires exact identification or overidentification.
D)is only possible if the number of instruments is the same as the number of regressors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
18
The rule-of-thumb for checking for weak instruments is as follows: for the case of a single endogenous regressor,
A)a first stage F must be statistically significant to indicate a strong instrument.
B)a first stage F > 1.96 indicates that the instruments are weak.
C)the t-statistic on each of the instruments must exceed at least 1.64.
D)a first stage F < 10 indicates that the instruments are weak.
A)a first stage F must be statistically significant to indicate a strong instrument.
B)a first stage F > 1.96 indicates that the instruments are weak.
C)the t-statistic on each of the instruments must exceed at least 1.64.
D)a first stage F < 10 indicates that the instruments are weak.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
19
The TSLS estimator is
A)consistent and has a normal distribution in large samples.
B)unbiased.
C)efficient in small samples.
D)F-distributed.
A)consistent and has a normal distribution in large samples.
B)unbiased.
C)efficient in small samples.
D)F-distributed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
20
The reduced form equation for X
A)regresses the endogenous variable X on the smallest possible subset of regressors.
B)relates the endogenous variable X to all the available exogenous variables,both those included in the regression of interest and the instruments.
C)uses the predicted values of X from the first stage as a regressor in the original equation.
D)uses smaller standard errors,such as homoskedasticity-only standard errors,for inference.
A)regresses the endogenous variable X on the smallest possible subset of regressors.
B)relates the endogenous variable X to all the available exogenous variables,both those included in the regression of interest and the instruments.
C)uses the predicted values of X from the first stage as a regressor in the original equation.
D)uses smaller standard errors,such as homoskedasticity-only standard errors,for inference.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
21
Write an essay about where valid instruments come from.Part of your explorations must deal with checking the validity of instruments and what the consequences of weak instruments are.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
22
To calculate the J-statistic you regress the
A)squared values of the TSLS residuals on all exogenous variables and the instruments.The statistic is then the number of observations times the regression R2.
B)TSLS residuals on all exogenous variables and the instruments.You then multiply the homoskedasticity-only F-statistic from that regression by the number of instruments.
C)OLS residuals from the reduced form on the instruments.The F-statistic from this regression is the J-statistic.
D)TSLS residuals on all exogenous variables and the instruments.You then multiply the heteroskedasticity-robust F-statistic from that regression by the number of instruments.
A)squared values of the TSLS residuals on all exogenous variables and the instruments.The statistic is then the number of observations times the regression R2.
B)TSLS residuals on all exogenous variables and the instruments.You then multiply the homoskedasticity-only F-statistic from that regression by the number of instruments.
C)OLS residuals from the reduced form on the instruments.The F-statistic from this regression is the J-statistic.
D)TSLS residuals on all exogenous variables and the instruments.You then multiply the heteroskedasticity-robust F-statistic from that regression by the number of instruments.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
23
For W to be an effective control variable in IV estimation,the following condition must hold
A)E(ui)= 0
B)E(ui|Zi,Wi)= E(ui|Wi)
C)E(uiuj)≠ 0
D)there must be an intercept in the regression
A)E(ui)= 0
B)E(ui|Zi,Wi)= E(ui|Wi)
C)E(uiuj)≠ 0
D)there must be an intercept in the regression

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
24
Describe the consequences of estimating an equation by OLS in the presence of an endogenous regressor.How can you overcome these obstacles? Present an alternative estimator and state its properties.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
25
To analyze the year-to-year variation in temperature data for a given city,you regress the daily high temperature (Temp)for 100 randomly selected days in two consecutive years (1997 and 1998)for Phoenix.The results are (heteroskedastic-robust standard errors in parenthesis):  = 15.63 + 0.80 ×
= 15.63 + 0.80 × 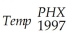 ;R2= 0.65,SER = 9.63
;R2= 0.65,SER = 9.63
(0.10)
(a)Calculate the predicted temperature for the current year if the temperature in the previous year was 40°F,78°F,and 100°F.How does this compare with you prior expectation? Sketch the regression line and compare it to the 45 degree line.What are the implications?
(b)You recall having studied errors-in-variables before.Although the web site you received your data from seems quite reliable in measuring data accurately,what if the temperature contained measurement error in the following sense: for any given day,say January 28,there is a true underlying seasonal temperature (X),but each year there are different temporary weather patterns (v,w)which result in a temperature different from X.For the two years in your data set,the situation can be described as follows:
different from X.For the two years in your data set,the situation can be described as follows: 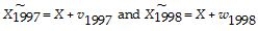
 Hence the population parameter for the intercept and slope are zero and one,as expected.It is not difficult to show that the OLS estimator for the slope is inconsistent,where
Hence the population parameter for the intercept and slope are zero and one,as expected.It is not difficult to show that the OLS estimator for the slope is inconsistent,where 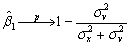 As a result you consider estimating the slope and intercept by TSLS.You think about an instrument and consider the temperature one month ahead of the observation in the previous year.Discuss instrument validity for this case.
As a result you consider estimating the slope and intercept by TSLS.You think about an instrument and consider the temperature one month ahead of the observation in the previous year.Discuss instrument validity for this case.
(c)The TSLS estimation result is as follows: = -6.24 + 1.07×
= -6.24 + 1.07× 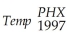 ;
;
(0.06)
Perform a t-test on whether or not the slope is now significantly different from one.
 = 15.63 + 0.80 ×
= 15.63 + 0.80 ×  ;R2= 0.65,SER = 9.63
;R2= 0.65,SER = 9.63(0.10)
(a)Calculate the predicted temperature for the current year if the temperature in the previous year was 40°F,78°F,and 100°F.How does this compare with you prior expectation? Sketch the regression line and compare it to the 45 degree line.What are the implications?
(b)You recall having studied errors-in-variables before.Although the web site you received your data from seems quite reliable in measuring data accurately,what if the temperature contained measurement error in the following sense: for any given day,say January 28,there is a true underlying seasonal temperature (X),but each year there are different temporary weather patterns (v,w)which result in a temperature
 different from X.For the two years in your data set,the situation can be described as follows:
different from X.For the two years in your data set,the situation can be described as follows: 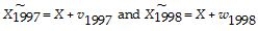
 Hence the population parameter for the intercept and slope are zero and one,as expected.It is not difficult to show that the OLS estimator for the slope is inconsistent,where
Hence the population parameter for the intercept and slope are zero and one,as expected.It is not difficult to show that the OLS estimator for the slope is inconsistent,where 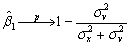 As a result you consider estimating the slope and intercept by TSLS.You think about an instrument and consider the temperature one month ahead of the observation in the previous year.Discuss instrument validity for this case.
As a result you consider estimating the slope and intercept by TSLS.You think about an instrument and consider the temperature one month ahead of the observation in the previous year.Discuss instrument validity for this case.(c)The TSLS estimation result is as follows:
 = -6.24 + 1.07×
= -6.24 + 1.07×  ;
;(0.06)
Perform a t-test on whether or not the slope is now significantly different from one.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
26
Studies of the effect of minimum wages on teenage employment typically regress the teenage employment to population ratio on the real minimum wage or the minimum wage relative to average hourly earnings using OLS.Assume that you have a cross section of United States for two years.Do you think that there are problems with simultaneous equation bias?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
27
Instrumental Variables regression uses instruments to
A)establish the Mozart Effect.
B)increase the regression R2.
C)eliminate serial correlation.
D)isolate movements in X that are uncorrelated with u.
A)establish the Mozart Effect.
B)increase the regression R2.
C)eliminate serial correlation.
D)isolate movements in X that are uncorrelated with u.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
28
In the case of exact identification
A)you can use the J-statistic in a test of overidentifying restrictions.
B)you cannot use TSLS for estimation purposes.
C)you must rely on your personal knowledge of the empirical problem at hand to assess whether the instruments are exogenous.
D)OLS and TSLS yield the same estimate.
A)you can use the J-statistic in a test of overidentifying restrictions.
B)you cannot use TSLS for estimation purposes.
C)you must rely on your personal knowledge of the empirical problem at hand to assess whether the instruments are exogenous.
D)OLS and TSLS yield the same estimate.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
29
Consider the following two equations to describe labor markets in various sectors of the economy Nd = β0 + β1 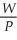 + u
+ u
Ns = γ0 + γ1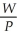 + v
+ v
Nd = Ns = N
A)W/P is exogenous,n is endogenous
B)Both n and W/P are endogenous
C)n is exogenous,W/P is endogenous
D)the parameters cannot be estimated because it would require two equations to be estimated at the same time (simultaneously)
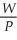 + u
+ uNs = γ0 + γ1
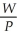 + v
+ vNd = Ns = N
A)W/P is exogenous,n is endogenous
B)Both n and W/P are endogenous
C)n is exogenous,W/P is endogenous
D)the parameters cannot be estimated because it would require two equations to be estimated at the same time (simultaneously)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
30
Using some of the examples from your textbook,describe econometric studies which required instrumental variable techniques.In each case emphasize why the need for instrumental variables arises and how authors have approached the problem.Make sure to include a discussion of overidentification,the validity of instruments,and testing procedures in your essay.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
31
(Requires Chapter 8)When using panel data and in the presence of endogenous regressors
A)the TSLS does not exist.
B)you do not have to worry about the validity of instruments,since there are so many fixed effects.
C)the OLS estimator is consistent.
D)application of the TSLS estimator is straightforward if you use two time periods and difference the data.
A)the TSLS does not exist.
B)you do not have to worry about the validity of instruments,since there are so many fixed effects.
C)the OLS estimator is consistent.
D)application of the TSLS estimator is straightforward if you use two time periods and difference the data.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
32
Let W be the included exogenous variables in a regression function that also has endogenous regressors (X).The W variables can
A)be control variables
B)have the property E(ui|Wi)= 0
C)make an instrument uncorrelated with u
D)all of the above
A)be control variables
B)have the property E(ui|Wi)= 0
C)make an instrument uncorrelated with u
D)all of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
33
In practice,the most difficult aspect of IV estimation is
A)finding instruments that are both relevant and exogenous.
B)that you have to use two stages in the estimation process.
C)calculating the J-statistic.
D)finding instruments that are exogenous.Relevant instruments are easy to find.
A)finding instruments that are both relevant and exogenous.
B)that you have to use two stages in the estimation process.
C)calculating the J-statistic.
D)finding instruments that are exogenous.Relevant instruments are easy to find.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
34
You have been hired as a consultant to estimate the demand for various brands of coffee in the market.You are provided with annual price data for two years by U.S.state and the quantities sold.You want to estimate a demand function for coffee using this data.What problems do you think you will encounter if you estimated the demand equation by OLS?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
35
The IV estimator can be used to potentially eliminate bias resulting from
A)multicollinearity.
B)serial correlation.
C)errors in variables.
D)heteroskedasticity.
A)multicollinearity.
B)serial correlation.
C)errors in variables.
D)heteroskedasticity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
36
You have estimated a government reaction function,i.e. ,a multiple regression equation,where a government instrument,say the federal funds rate,depends on past government target variables,such as inflation and unemployment rates.In addition,you added the previous period's popularity deficit of the government,e.g.the (approval rating of the president - 50%),as one of the regressors.Your idea is that the Federal Reserve,although formally independent,will try to expand the economy if the president is unpopular.One of your peers,a political science student,points out that approval ratings depend on the state of the economy and thereby indirectly on government instruments.It is therefore endogenous and should be estimated along with the reaction function.Initially you want to reply by using a phrase that includes the words "money neutrality" but are worried about a lengthy debate.Instead you state that as an economist,you are not concerned about government approval ratings,and that government approval ratings are determined outside your (the economic)model.Does your whim make the regressor exogenous? Why or why not?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
37
The logic of control variables in IV regressions
A)parallels the logic of control variables in OLS
B)only applies in the case of homoskedastic errors in the first stage of two stage least squares estimation
C)is different in a substantial way from the logic of control variables in OLS since there are two stages in estimation
D)implies that the TSLS is efficient
A)parallels the logic of control variables in OLS
B)only applies in the case of homoskedastic errors in the first stage of two stage least squares estimation
C)is different in a substantial way from the logic of control variables in OLS since there are two stages in estimation
D)implies that the TSLS is efficient

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
38
Endogenous variables
A)are correlated with the error term.
B)always appear on the LHS of regression functions.
C)cannot be regressors.
D)are uncorrelated with the error term.
A)are correlated with the error term.
B)always appear on the LHS of regression functions.
C)cannot be regressors.
D)are uncorrelated with the error term.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
39
Consider a model with one endogenous regressor and two instruments.Then the J-statistic will be large
A)if the number of observations are very large.
B)if the coefficients are very different when estimating the coefficients using one instrument at a time.
C)if the TSLS estimates are very different from the OLS estimates.
D)when you use homoskedasticity-only standard errors.
A)if the number of observations are very large.
B)if the coefficients are very different when estimating the coefficients using one instrument at a time.
C)if the TSLS estimates are very different from the OLS estimates.
D)when you use homoskedasticity-only standard errors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
40
Write a short essay about the Overidentifying Restrictions Test.What is meant exactly by "overidentification?" State the null hypothesis.Describe how to calculate the J-statistic and what its distribution is.Use an example of two instruments and one endogenous variable to explain under what situation the test will be likely to reject the null hypothesis.What does this example tell you about the exactly identified case? If your variables pass the test,is this sufficient for these variables to be good instruments?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
41
Consider the following model of demand and supply of coffee:
Demand: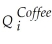 = β1
= β1 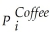 + β2
+ β2 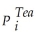 + ui
+ ui
Supply: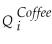 = β3
= β3 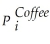 + β4
+ β4 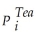 + β5Weather + vi
+ β5Weather + vi
(variables are measure in deviations from means,so that the constant is omitted).
What are the expected signs of the various coefficients this model? Assume that the price of tea and Weather are exogenous variables.Are the coefficients in the supply equation identified? Are the coefficients in the demand equation identified? Are they overidentified? Is this result surprising given that there are more exogenous regressors in the second equation?
Demand:
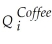 = β1
= β1 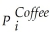 + β2
+ β2 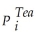 + ui
+ uiSupply:
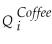 = β3
= β3 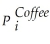 + β4
+ β4 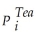 + β5Weather + vi
+ β5Weather + vi(variables are measure in deviations from means,so that the constant is omitted).
What are the expected signs of the various coefficients this model? Assume that the price of tea and Weather are exogenous variables.Are the coefficients in the supply equation identified? Are the coefficients in the demand equation identified? Are they overidentified? Is this result surprising given that there are more exogenous regressors in the second equation?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
42
Here are some examples of the instrumental variables regression model.In each case you are given the number of instruments and the J-statistic.Find the relevant value from the 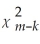 distribution,using a 1% and 5% significance level,and make a decision whether or not to reject the null hypothesis.
distribution,using a 1% and 5% significance level,and make a decision whether or not to reject the null hypothesis.
(a)Yi = β0 + β1X1i + ui,i = 1,... ,n;Z1i,Z2i are valid instruments,J = 2.58.
(b)Yi = β0 + β1X1i + β2X2i + β3W1i + ui,i = 1,... ,n;Z1i,Z2i,Z3i,Z4i are valid instruments,J = 9.63.
(c)Yi = β0 + β1X1i + β2W1i + β3W2i + β4W3i + ui,i = 1,... ,n;Z1i,Z2i,Z3i,Z4i are valid instruments,J = 11.86.
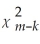 distribution,using a 1% and 5% significance level,and make a decision whether or not to reject the null hypothesis.
distribution,using a 1% and 5% significance level,and make a decision whether or not to reject the null hypothesis.(a)Yi = β0 + β1X1i + ui,i = 1,... ,n;Z1i,Z2i are valid instruments,J = 2.58.
(b)Yi = β0 + β1X1i + β2X2i + β3W1i + ui,i = 1,... ,n;Z1i,Z2i,Z3i,Z4i are valid instruments,J = 9.63.
(c)Yi = β0 + β1X1i + β2W1i + β3W2i + β4W3i + ui,i = 1,... ,n;Z1i,Z2i,Z3i,Z4i are valid instruments,J = 11.86.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
43
Consider the following population regression model relating the dependent variable Yi and regressor Xi,
Yi = β0 + β1Xi + ui,i = 1,…,n.
Xi ≡ Yi + Zi
where Z is a valid instrument for X.
(a)Explain why you should not use OLS to estimate β1.
(b)To generate a consistent estimator for β1,what should you do?
(c)The two equations above make up a system of equations in two unknowns.Specify the two reduced form equations in terms of the original coefficients.(Hint: substitute the identity into the first equation and solve for Y.Similarly,substitute Y into the identity and solve for X. )
(d)Do the two reduced form equations satisfy the OLS assumptions? If so,can you find consistent estimators of the two slopes? What is the ratio of the two estimated slopes? This estimator is called "Indirect Least Squares." How does it compare to the TSLS in this example?
Yi = β0 + β1Xi + ui,i = 1,…,n.
Xi ≡ Yi + Zi
where Z is a valid instrument for X.
(a)Explain why you should not use OLS to estimate β1.
(b)To generate a consistent estimator for β1,what should you do?
(c)The two equations above make up a system of equations in two unknowns.Specify the two reduced form equations in terms of the original coefficients.(Hint: substitute the identity into the first equation and solve for Y.Similarly,substitute Y into the identity and solve for X. )
(d)Do the two reduced form equations satisfy the OLS assumptions? If so,can you find consistent estimators of the two slopes? What is the ratio of the two estimated slopes? This estimator is called "Indirect Least Squares." How does it compare to the TSLS in this example?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
44
You started your econometrics course by studying the OLS estimator extensively,first for the simple regression case and then for extensions of it.You have now learned about the instrumental variable estimator.Under what situation would you prefer one to the other? Be specific in explaining under which situations one estimation method generates superior results.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
45
Earnings functions,whereby the log of earnings is regressed on years of education,years of on the job training,and individual characteristics,have been studied for a variety of reasons.Some studies have focused on the returns to education,others on discrimination,union non-union differentials,etc.For all these studies,a major concern has been the fact that ability should enter as a determinant of earnings,but that it is close to impossible to measure and therefore represents an omitted variable.
Assume that the coefficient on years of education is the parameter of interest.Given that education is positively correlated to ability,since,for example,more able students attract scholarships and hence receive more years of education,the OLS estimator for the returns to education could be upward biased.To overcome this problem,various authors have used instrumental variable estimation techniques.For each of the instruments potential instruments listed below briefly discuss instrument validity.
(a)The individual's postal zip code.
(b)The individual's IQ or testscore on a work related exam.
(c)Years of education for the individual's mother or father.
(d)Number of siblings the individual has.
Assume that the coefficient on years of education is the parameter of interest.Given that education is positively correlated to ability,since,for example,more able students attract scholarships and hence receive more years of education,the OLS estimator for the returns to education could be upward biased.To overcome this problem,various authors have used instrumental variable estimation techniques.For each of the instruments potential instruments listed below briefly discuss instrument validity.
(a)The individual's postal zip code.
(b)The individual's IQ or testscore on a work related exam.
(c)Years of education for the individual's mother or father.
(d)Number of siblings the individual has.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
46
The two conditions for instrument validity are corr(Zi,Xi)≠ 0 and corr(Zi,ui)= 0.The reason for the inconsistency of OLS is that corr(Xi,ui)≠ 0.But if X and Z are correlated,and X and u are also correlated,then how can Z and u not be correlated? Explain.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
47
Consider the a model of the U.S.labor market where the demand for labor depends on the real wage,while the supply of labor is vertical and does not depend on the real wage.You could argue that the supply of labor by households (think of hours supplied by two adults and two children)has not changed much over the last 60 years or so in the U.S.while real wages more than doubled over the same time span.At first that seems strange given the higher participation rate of females over that period,but that increase has been countered by a lower male participation rate (resulting from earlier retirement),an increase in legal holidays,and an increase in vacation days.
a.Write down two equations representing the labor supply and labor demand function,allowing for an error term in each of the demand and supply equation.In addition,assume that the labor market clears.
b.How would you estimate the labor supply equation?
c.Assuming that the error terms are mutually independent i.i.d.random variables,both with mean zero,show that the real wage and the error term of the labor demand equation are correlated.
d.If you find a non-zero correlation,should you estimate the labor demand equation using OLS? If so,what are the consequences?
e.Estimating the labor demand equation by IV estimation,which instrument suggests itself immediately?
a.Write down two equations representing the labor supply and labor demand function,allowing for an error term in each of the demand and supply equation.In addition,assume that the labor market clears.
b.How would you estimate the labor supply equation?
c.Assuming that the error terms are mutually independent i.i.d.random variables,both with mean zero,show that the real wage and the error term of the labor demand equation are correlated.
d.If you find a non-zero correlation,should you estimate the labor demand equation using OLS? If so,what are the consequences?
e.Estimating the labor demand equation by IV estimation,which instrument suggests itself immediately?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
48
Your textbook gave an example of attempting to estimate the demand for a good in a market,but being unable to do so because the demand function was not identified.Is this the case for every market? Consider,for example,the demand for sports events.One of your peers estimated the following demand function after collecting data over two years for every one of the 162 home games of the 2000 and 2001 season for the Los Angeles Dodgers.  = 15,005 + 201 × Temperat + 465 × DodgNetWin + 82 × OppNetWin
= 15,005 + 201 × Temperat + 465 × DodgNetWin + 82 × OppNetWin
(8,770)(121)(169)(26)
+ 9647 × DFSaSu + 1328 × Drain + 1609 × D150m + 271 × DDiv - 978 × D2001;
(1505)(3355)(1819)(1,184)(1,143)
R2 = 0.416,SER = 6983
Where Attend is announced stadium attendance,Temperat it the average temperature on game day,DodgNetWin are the net wins of the Dodgers before the game (wins-losses),OppNetWin is the opposing team's net wins at the end of the previous season,and DFSaSu,Drain,D150m,Ddiv,and D2001 are binary variables,taking a value of 1 if the game was played on a weekend,it rained during that day,the opposing team was within a 150 mile radius,plays in the same division as the Dodgers,and during 2001,respectively.Numbers in parenthesis are heteroskedasticity- robust standard errors.
Even if there is no identification problem,is it likely that all regressors are uncorrelated with the error term? If not,what are the consequences?
 = 15,005 + 201 × Temperat + 465 × DodgNetWin + 82 × OppNetWin
= 15,005 + 201 × Temperat + 465 × DodgNetWin + 82 × OppNetWin(8,770)(121)(169)(26)
+ 9647 × DFSaSu + 1328 × Drain + 1609 × D150m + 271 × DDiv - 978 × D2001;
(1505)(3355)(1819)(1,184)(1,143)
R2 = 0.416,SER = 6983
Where Attend is announced stadium attendance,Temperat it the average temperature on game day,DodgNetWin are the net wins of the Dodgers before the game (wins-losses),OppNetWin is the opposing team's net wins at the end of the previous season,and DFSaSu,Drain,D150m,Ddiv,and D2001 are binary variables,taking a value of 1 if the game was played on a weekend,it rained during that day,the opposing team was within a 150 mile radius,plays in the same division as the Dodgers,and during 2001,respectively.Numbers in parenthesis are heteroskedasticity- robust standard errors.
Even if there is no identification problem,is it likely that all regressors are uncorrelated with the error term? If not,what are the consequences?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
49
To study the determinants of growth between the countries of the world,researchers have used panels of countries and observations spanning over long periods of time .Some of these studies have focused on the effect that inflation has on growth and found that although the effect is small for a given time period,it accumulates over time and therefore has an important negative effect.
(a)Explain why the OLS estimator may be biased in this case.
(b)Explain how methods using panel data could potentially alleviate the problem.
(c)Some authors have suggested using an index of central bank independence as an instrumental.Discuss whether or not such an index would be a valid instrument.
(a)Explain why the OLS estimator may be biased in this case.
(b)Explain how methods using panel data could potentially alleviate the problem.
(c)Some authors have suggested using an index of central bank independence as an instrumental.Discuss whether or not such an index would be a valid instrument.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
50
(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as
Y = Xβ + U
where
Y =![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e5_896a_7f0c3dda6078_TB2833_11.jpg) ,U =
,U = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e6_896a_6d2e94f2d092_TB2833_11.jpg) ,X =
,X = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e7_896a_6bdda3b19972_TB2833_11.jpg) ,and β =
,and β = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0f8_896a_57c8d097b8c9_TB2833_11.jpg) Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous).
Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous).
The instrumental variable estimator for the overidentified case is![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0f9_896a_53308949d5e9_TB2833_11.jpg) where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables.
where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables.
Z =![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fa_896a_3b05b78dda27_TB2833_11.jpg) It is of order n × (m+r+1).
It is of order n × (m+r+1).
For this estimator to exist,both (![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fb_896a_71b246d1f668_TB2833_11.jpg) Z)and [
Z)and [ ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fc_896a_43d802456eb0_TB2833_11.jpg) Z(
Z( ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fd_896a_2dc3f5bef957_TB2833_11.jpg) Z)-1
Z)-1 ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fe_896a_25f5de80a00a_TB2833_11.jpg) X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.
X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.
Y = Xβ + U
where
Y =
![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e5_896a_7f0c3dda6078_TB2833_11.jpg) ,U =
,U = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e6_896a_6d2e94f2d092_TB2833_11.jpg) ,X =
,X = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_99e7_896a_6bdda3b19972_TB2833_11.jpg) ,and β =
,and β = ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0f8_896a_57c8d097b8c9_TB2833_11.jpg) Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous).
Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous).The instrumental variable estimator for the overidentified case is
![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0f9_896a_53308949d5e9_TB2833_11.jpg) where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables.
where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables.Z =
![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fa_896a_3b05b78dda27_TB2833_11.jpg) It is of order n × (m+r+1).
It is of order n × (m+r+1).For this estimator to exist,both (
![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fb_896a_71b246d1f668_TB2833_11.jpg) Z)and [
Z)and [ ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fc_896a_43d802456eb0_TB2833_11.jpg) Z(
Z( ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fd_896a_2dc3f5bef957_TB2833_11.jpg) Z)-1
Z)-1 ![(Requires Matrix Algebra)The population multiple regression model can be written in matrix form as Y = Xβ + U where Y = ,U = ,X = ,and β = Note that the X matrix contains both k endogenous regressors and (r +1)included exogenous regressors (the constant is obviously exogenous). The instrumental variable estimator for the overidentified case is where Z is a matrix,which contains two types of variables: first the r included exogenous regressors plus the constant,and second,m instrumental variables. Z = It is of order n × (m+r+1). For this estimator to exist,both ( Z)and [ Z( Z)-1 X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd89_c0fe_896a_25f5de80a00a_TB2833_11.jpg) X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.
X] must be invertible.State the conditions under which this will be the case and relate them to the degree of overidentification.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck








