Deck 11: Regression With a Binary Dependent Variable
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/50
العب
ملء الشاشة (f)
Deck 11: Regression With a Binary Dependent Variable
1
When having a choice of which estimator to use with a binary dependent variable,use
A)probit or logit depending on which method is easiest to use in the software package at hand.
B)probit for extreme values of X and the linear probability model for values in between.
C)OLS (linear probability model)since it is easier to interpret.
D)the estimation method which results in estimates closest to your prior expectations.
A)probit or logit depending on which method is easiest to use in the software package at hand.
B)probit for extreme values of X and the linear probability model for values in between.
C)OLS (linear probability model)since it is easier to interpret.
D)the estimation method which results in estimates closest to your prior expectations.
A
2
The binary dependent variable model is an example of a
A)regression model,which has as a regressor,among others,a binary variable.
B)model that cannot be estimated by OLS.
C)limited dependent variable model.
D)model where the left-hand variable is measured in base 2.
A)regression model,which has as a regressor,among others,a binary variable.
B)model that cannot be estimated by OLS.
C)limited dependent variable model.
D)model where the left-hand variable is measured in base 2.
C
3
The logit model derives its name from
A)the logarithmic model.
B)the probit model.
C)the logistic function.
D)the tobit model.
A)the logarithmic model.
B)the probit model.
C)the logistic function.
D)the tobit model.
C
4
Nonlinear least squares
A)solves the minimization of the sum of squared predictive mistakes through sophisticated mathematical routines,essentially by trial and error methods.
B)should always be used when you have nonlinear equations.
C)gives you the same results as maximum likelihood estimation.
D)is another name for sophisticated least squares.
A)solves the minimization of the sum of squared predictive mistakes through sophisticated mathematical routines,essentially by trial and error methods.
B)should always be used when you have nonlinear equations.
C)gives you the same results as maximum likelihood estimation.
D)is another name for sophisticated least squares.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
5
In the binary dependent variable model,a predicted value of 0.6 means that
A)the most likely value the dependent variable will take on is 60 percent.
B)given the values for the explanatory variables,there is a 60 percent probability that the dependent variable will equal one.
C)the model makes little sense,since the dependent variable can only be 0 or 1.
D)given the values for the explanatory variables,there is a 40 percent probability that the dependent variable will equal one.
A)the most likely value the dependent variable will take on is 60 percent.
B)given the values for the explanatory variables,there is a 60 percent probability that the dependent variable will equal one.
C)the model makes little sense,since the dependent variable can only be 0 or 1.
D)given the values for the explanatory variables,there is a 40 percent probability that the dependent variable will equal one.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
6
(Requires Advanced material)Only one of the following models can be estimated by OLS:
A)Y = AKαLβ + u.
B)Pr(Y = 1 X)= Φ(β0 + β1X)
X)= Φ(β0 + β1X)
C)Pr(Y = 1 X)= F(β0 + β1X)=
X)= F(β0 + β1X)=
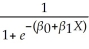 .
.
D)Y = AKα Lβu.
A)Y = AKαLβ + u.
B)Pr(Y = 1
 X)= Φ(β0 + β1X)
X)= Φ(β0 + β1X)C)Pr(Y = 1
 X)= F(β0 + β1X)=
X)= F(β0 + β1X)=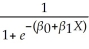 .
.D)Y = AKα Lβu.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
7
In the probit model Pr(Y = 1  X1,X2,... ,Xk)= Φ(β0 + β1X1 + βxX2 + ...+ βkXk),
X1,X2,... ,Xk)= Φ(β0 + β1X1 + βxX2 + ...+ βkXk),
A)the β's do not have a simple interpretation.
B)the slopes tell you the effect of a unit increase in X on the probability of Y.
C)β0 cannot be negative since probabilities have to lie between 0 and 1.
D)β0 is the probability of observing Y when all X's are 0
 X1,X2,... ,Xk)= Φ(β0 + β1X1 + βxX2 + ...+ βkXk),
X1,X2,... ,Xk)= Φ(β0 + β1X1 + βxX2 + ...+ βkXk),A)the β's do not have a simple interpretation.
B)the slopes tell you the effect of a unit increase in X on the probability of Y.
C)β0 cannot be negative since probabilities have to lie between 0 and 1.
D)β0 is the probability of observing Y when all X's are 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
8
The following tools from multiple regression analysis carry over in a meaningful manner to the linear probability model,with the exception of the
A)F-statistic.
B)significance test using the t-statistic.
C)95% confidence interval using ± 1.96 times the standard error.
D)regression R2.
A)F-statistic.
B)significance test using the t-statistic.
C)95% confidence interval using ± 1.96 times the standard error.
D)regression R2.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
9
(Requires Appendix material)The following are examples of limited dependent variables,with the exception of
A)binary dependent variable.
B)log-log specification.
C)truncated regression model.
D)discrete choice model.
A)binary dependent variable.
B)log-log specification.
C)truncated regression model.
D)discrete choice model.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
10
E(Y  X1,... ,Xk)= Pr(Y = 1
X1,... ,Xk)= Pr(Y = 1  X1,... ,Xk)means that
X1,... ,Xk)means that
A)for a binary variable model,the predicted value from the population regression is the probability that Y=1,given X.
B)dividing Y by the X's is the same as the probability of Y being the inverse of the sum of the X's.
C)the exponential of Y is the same as the probability of Y happening.
D)you are pretty certain that Y takes on a value of 1 given the X's.
 X1,... ,Xk)= Pr(Y = 1
X1,... ,Xk)= Pr(Y = 1  X1,... ,Xk)means that
X1,... ,Xk)means thatA)for a binary variable model,the predicted value from the population regression is the probability that Y=1,given X.
B)dividing Y by the X's is the same as the probability of Y being the inverse of the sum of the X's.
C)the exponential of Y is the same as the probability of Y happening.
D)you are pretty certain that Y takes on a value of 1 given the X's.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
11
(Requires material from Section 11.3 - possibly skipped)For the measure of fit in your regression model with a binary dependent variable,you can meaningfully use the
A)regression R2.
B)size of the regression coefficients.
C)pseudo R2.
D)standard error of the regression.
A)regression R2.
B)size of the regression coefficients.
C)pseudo R2.
D)standard error of the regression.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
12
The maximum likelihood estimation method produces,in general,all of the following desirable properties with the exception of
A)efficiency.
B)consistency.
C)normally distributed estimators in large samples.
D)unbiasedness in small samples.
A)efficiency.
B)consistency.
C)normally distributed estimators in large samples.
D)unbiasedness in small samples.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
13
The logit model can be estimated and yields consistent estimates if you are using
A)OLS estimation.
B)maximum likelihood estimation.
C)differences in means between those individuals with a dependent variable equal to one and those with a dependent variable equal to zero.
D)the linear probability model.
A)OLS estimation.
B)maximum likelihood estimation.
C)differences in means between those individuals with a dependent variable equal to one and those with a dependent variable equal to zero.
D)the linear probability model.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
14
The major flaw of the linear probability model is that
A)the actuals can only be 0 and 1,but the predicted are almost always different from that.
B)the regression R2 cannot be used as a measure of fit.
C)people do not always make clear-cut decisions.
D)the predicted values can lie above 1 and below 0.
A)the actuals can only be 0 and 1,but the predicted are almost always different from that.
B)the regression R2 cannot be used as a measure of fit.
C)people do not always make clear-cut decisions.
D)the predicted values can lie above 1 and below 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
15
In the expression Pr(deny = 1  P/I Ratio,black)= Φ(-2.26 + 2.74P/I ratio + 0.71black),the effect of increasing the P/I ratio from 0.3 to 0.4 for a white person
P/I Ratio,black)= Φ(-2.26 + 2.74P/I ratio + 0.71black),the effect of increasing the P/I ratio from 0.3 to 0.4 for a white person
A)is 0.274 percentage points.
B)is 6.1 percentage points.
C)should not be interpreted without knowledge of the regression R2.
D)is 2.74 percentage points.
 P/I Ratio,black)= Φ(-2.26 + 2.74P/I ratio + 0.71black),the effect of increasing the P/I ratio from 0.3 to 0.4 for a white person
P/I Ratio,black)= Φ(-2.26 + 2.74P/I ratio + 0.71black),the effect of increasing the P/I ratio from 0.3 to 0.4 for a white personA)is 0.274 percentage points.
B)is 6.1 percentage points.
C)should not be interpreted without knowledge of the regression R2.
D)is 2.74 percentage points.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
16
In the probit model Pr(Y = 1  = Φ(β0 + β1X),Φ
= Φ(β0 + β1X),Φ
A)is not defined for Φ(0).
B)is the standard normal cumulative distribution function.
C)is set to 1.96.
D)can be computed from the standard normal density function.
 = Φ(β0 + β1X),Φ
= Φ(β0 + β1X),ΦA)is not defined for Φ(0).
B)is the standard normal cumulative distribution function.
C)is set to 1.96.
D)can be computed from the standard normal density function.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
17
The probit model
A)is the same as the logit model.
B)always gives the same fit for the predicted values as the linear probability model for values between 0.1 and 0.9.
C)forces the predicted values to lie between 0 and 1.
D)should not be used since it is too complicated.
A)is the same as the logit model.
B)always gives the same fit for the predicted values as the linear probability model for values between 0.1 and 0.9.
C)forces the predicted values to lie between 0 and 1.
D)should not be used since it is too complicated.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
18
In the linear probability model,the interpretation of the slope coefficient is
A)the change in odds associated with a unit change in X,holding other regressors constant.
B)not all that meaningful since the dependent variable is either 0 or 1.
C)the change in probability that Y=1 associated with a unit change in X,holding others regressors constant.
D)the response in the dependent variable to a percentage change in the regressor.
A)the change in odds associated with a unit change in X,holding other regressors constant.
B)not all that meaningful since the dependent variable is either 0 or 1.
C)the change in probability that Y=1 associated with a unit change in X,holding others regressors constant.
D)the response in the dependent variable to a percentage change in the regressor.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
19
The linear probability model is
A)the application of the multiple regression model with a continuous left-hand side variable and a binary variable as at least one of the regressors.
B)an example of probit estimation.
C)another word for logit estimation.
D)the application of the linear multiple regression model to a binary dependent variable.
A)the application of the multiple regression model with a continuous left-hand side variable and a binary variable as at least one of the regressors.
B)an example of probit estimation.
C)another word for logit estimation.
D)the application of the linear multiple regression model to a binary dependent variable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
20
In the expression Pr(Y = 1  = Φ(β0 + β1X),
= Φ(β0 + β1X),
A)(β0 + β1X)plays the role of z in the cumulative standard normal distribution function.
B)β1 cannot be negative since probabilities have to lie between 0 and 1.
C)β0 cannot be negative since probabilities have to lie between 0 and 1.
D)min (β0 + β1X)> 0 since probabilities have to lie between 0 and 1.
 = Φ(β0 + β1X),
= Φ(β0 + β1X),A)(β0 + β1X)plays the role of z in the cumulative standard normal distribution function.
B)β1 cannot be negative since probabilities have to lie between 0 and 1.
C)β0 cannot be negative since probabilities have to lie between 0 and 1.
D)min (β0 + β1X)> 0 since probabilities have to lie between 0 and 1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
21
The following problems could be analyzed using probit and logit estimation with the exception of whether or not
A)a college student decides to study abroad for one semester.
B)being a female has an effect on earnings.
C)a college student will attend a certain college after being accepted.
D)applicants will default on a loan.
A)a college student decides to study abroad for one semester.
B)being a female has an effect on earnings.
C)a college student will attend a certain college after being accepted.
D)applicants will default on a loan.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
22
Consider the following logit regression:
Pr(Y = 1 X)= F (15.3 - 0.24 × X)
X)= F (15.3 - 0.24 × X)
Calculate the change in probability for X increasing by 10 for X = 40 and X = 60.Why is there such a large difference in the change in probabilities?
Pr(Y = 1
 X)= F (15.3 - 0.24 × X)
X)= F (15.3 - 0.24 × X)Calculate the change in probability for X increasing by 10 for X = 40 and X = 60.Why is there such a large difference in the change in probabilities?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
23
A study investigated the impact of house price appreciation on household mobility.The underlying idea was that if a house were viewed as one part of the household's portfolio,then changes in the value of the house,relative to other portfolio items,should result in investment decisions altering the current portfolio.Using 5,162 observations,the logit equation was estimated as shown in the table,where the limited dependent variable is one if the household moved in 1978 and is zero if the household did not move:
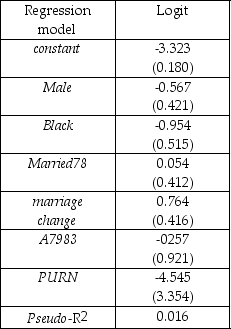 where male,black,married78,and marriage change are binary variables.They indicate,respectively,if the entity was a male-headed household,a black household,was married,and whether a change in marital status occurred between 1977 and 1978.A7983 is the appreciation rate for each house from 1979 to 1983 minus the SMSA-wide rate of appreciation for the same time period,and PNRN is a predicted appreciation rate for the unit minus the national average rate.
where male,black,married78,and marriage change are binary variables.They indicate,respectively,if the entity was a male-headed household,a black household,was married,and whether a change in marital status occurred between 1977 and 1978.A7983 is the appreciation rate for each house from 1979 to 1983 minus the SMSA-wide rate of appreciation for the same time period,and PNRN is a predicted appreciation rate for the unit minus the national average rate.
(a)Interpret the results.Comment on the statistical significance of the coefficients.Do the slope coefficients lend themselves to easy interpretation?
(b)The mean values for the regressors are as shown in the accompanying table.
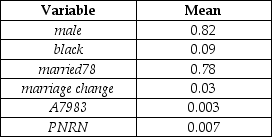 Taking the coefficients at face value and using the sample means,calculate the probability of a household moving.
Taking the coefficients at face value and using the sample means,calculate the probability of a household moving.
(c)Given this probability,what would be the effect of a decrease in the predicted appreciation rate of 20 percent,that is A7983 = -0.20?
 where male,black,married78,and marriage change are binary variables.They indicate,respectively,if the entity was a male-headed household,a black household,was married,and whether a change in marital status occurred between 1977 and 1978.A7983 is the appreciation rate for each house from 1979 to 1983 minus the SMSA-wide rate of appreciation for the same time period,and PNRN is a predicted appreciation rate for the unit minus the national average rate.
where male,black,married78,and marriage change are binary variables.They indicate,respectively,if the entity was a male-headed household,a black household,was married,and whether a change in marital status occurred between 1977 and 1978.A7983 is the appreciation rate for each house from 1979 to 1983 minus the SMSA-wide rate of appreciation for the same time period,and PNRN is a predicted appreciation rate for the unit minus the national average rate.(a)Interpret the results.Comment on the statistical significance of the coefficients.Do the slope coefficients lend themselves to easy interpretation?
(b)The mean values for the regressors are as shown in the accompanying table.
 Taking the coefficients at face value and using the sample means,calculate the probability of a household moving.
Taking the coefficients at face value and using the sample means,calculate the probability of a household moving.(c)Given this probability,what would be the effect of a decrease in the predicted appreciation rate of 20 percent,that is A7983 = -0.20?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
24
(Requires Advanced material)Nonlinear least squares estimators in general are not
A)consistent.
B)normally distributed in large samples.
C)efficient.
D)used in econometrics.
A)consistent.
B)normally distributed in large samples.
C)efficient.
D)used in econometrics.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
25
A study analyzed the probability of Major League Baseball (MLB)players to "survive" for another season,or,in other words,to play one more season.The researchers had a sample of 4,728 hitters and 3,803 pitchers for the years 1901-1999.All explanatory variables are standardized.The probit estimation yielded the results as shown in the table:
 where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.
where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.
(a)Interpret the two probit equations and calculate survival probabilities for hitters and pitchers at the sample mean.Why are these so high?
(b)Calculate the change in the survival probability for a player who has a very bad year by performing two standard deviations below the average (assume also that this player has been in the majors for many years so that his average performance is hardly affected).How does this change the survival probability when compared to the answer in (a)?
(c)Since the results seem similar,the researcher could consider combining the two samples.Explain in some detail how this could be done and how you could test the hypothesis that the coefficients are the same.
 where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.
where the limited dependent variable takes on a value of one if the player had one more season (a minimum of 50 at bats or 25 innings pitched),number of seasons played is measured in years,performance is the batting average for hitters and the earned run average for pitchers,and average performance refers to performance over the career.(a)Interpret the two probit equations and calculate survival probabilities for hitters and pitchers at the sample mean.Why are these so high?
(b)Calculate the change in the survival probability for a player who has a very bad year by performing two standard deviations below the average (assume also that this player has been in the majors for many years so that his average performance is hardly affected).How does this change the survival probability when compared to the answer in (a)?
(c)Since the results seem similar,the researcher could consider combining the two samples.Explain in some detail how this could be done and how you could test the hypothesis that the coefficients are the same.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
26
When estimating probit and logit models,
A)the t-statistic should still be used for testing a single restriction.
B)you cannot have binary variables as explanatory variables as well.
C)F-statistics should not be used,since the models are nonlinear.
D)it is no longer true that the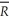 2 < R2.
2 < R2.
A)the t-statistic should still be used for testing a single restriction.
B)you cannot have binary variables as explanatory variables as well.
C)F-statistics should not be used,since the models are nonlinear.
D)it is no longer true that the
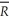 2 < R2.
2 < R2.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
27
A study tried to find the determinants of the increase in the number of households headed by a female.Using 1940 and 1960 historical census data,a logit model was estimated to predict whether a woman is the head of a household (living on her own)or whether she is living within another's household.The limited dependent variable takes on a value of one if the female lives on her own and is zero if she shares housing.The results for 1960 using 6,051 observations on prime-age whites and 1,294 on nonwhites were as shown in the table:
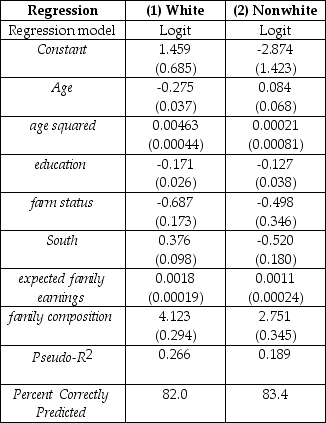 where age is measured in years,education is years of schooling of the family head,farm status is a binary variable taking the value of one if the family head lived on a farm,south is a binary variable for living in a certain region of the country,expected family earnings was generated from a separate OLS regression to predict earnings from a set of regressors,and family composition refers to the number of family members under the age of 18 divided by the total number in the family.
where age is measured in years,education is years of schooling of the family head,farm status is a binary variable taking the value of one if the family head lived on a farm,south is a binary variable for living in a certain region of the country,expected family earnings was generated from a separate OLS regression to predict earnings from a set of regressors,and family composition refers to the number of family members under the age of 18 divided by the total number in the family.
The mean values for the variables were as shown in the table.
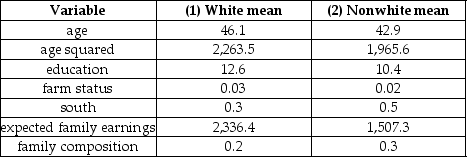 (a)Interpret the results.Do the coefficients have the expected signs? Why do you think age was entered both in levels and in squares?
(a)Interpret the results.Do the coefficients have the expected signs? Why do you think age was entered both in levels and in squares?
(b)Calculate the difference in the predicted probability between whites and nonwhites at the sample mean values of the explanatory variables.Why do you think the study did not combine the observations and allowed for a nonwhite binary variable to enter?
(c)What would be the effect on the probability of a nonwhite woman living on her own,if education and family composition were changed from their current mean to the mean of whites,while all other variables were left unchanged at the nonwhite mean values?
 where age is measured in years,education is years of schooling of the family head,farm status is a binary variable taking the value of one if the family head lived on a farm,south is a binary variable for living in a certain region of the country,expected family earnings was generated from a separate OLS regression to predict earnings from a set of regressors,and family composition refers to the number of family members under the age of 18 divided by the total number in the family.
where age is measured in years,education is years of schooling of the family head,farm status is a binary variable taking the value of one if the family head lived on a farm,south is a binary variable for living in a certain region of the country,expected family earnings was generated from a separate OLS regression to predict earnings from a set of regressors,and family composition refers to the number of family members under the age of 18 divided by the total number in the family.The mean values for the variables were as shown in the table.
 (a)Interpret the results.Do the coefficients have the expected signs? Why do you think age was entered both in levels and in squares?
(a)Interpret the results.Do the coefficients have the expected signs? Why do you think age was entered both in levels and in squares?(b)Calculate the difference in the predicted probability between whites and nonwhites at the sample mean values of the explanatory variables.Why do you think the study did not combine the observations and allowed for a nonwhite binary variable to enter?
(c)What would be the effect on the probability of a nonwhite woman living on her own,if education and family composition were changed from their current mean to the mean of whites,while all other variables were left unchanged at the nonwhite mean values?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
28
To measure the fit of the probit model,you should:
A)use the regression R2.
B)plot the predicted values and see how closely they match the actuals.
C)use the log of the likelihood function and compare it to the value of the likelihood function.
D)use the fraction correctly predicted or the pseudo R2.
A)use the regression R2.
B)plot the predicted values and see how closely they match the actuals.
C)use the log of the likelihood function and compare it to the value of the likelihood function.
D)use the fraction correctly predicted or the pseudo R2.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
29
Probit coefficients are typically estimated using
A)the OLS method
B)the method of maximum likelihood
C)non-linear least squares (NLLS)
D)by transforming the estimates from the linear probability model
A)the OLS method
B)the method of maximum likelihood
C)non-linear least squares (NLLS)
D)by transforming the estimates from the linear probability model

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
30
In the probit regression,the coefficient β1 indicates
A)the change in the probability of Y = 1 given a unit change in X
B)the change in the probability of Y = 1 given a percent change in X
C)the change in the z- value associated with a unit change in X
D)none of the above
A)the change in the probability of Y = 1 given a unit change in X
B)the change in the probability of Y = 1 given a percent change in X
C)the change in the z- value associated with a unit change in X
D)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
31
The logit regression (11.10)on page 393 of your textbook reads: 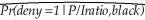 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)
(a)Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X, i =
i = 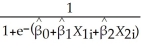 where
where 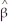 0 = -4.13,
0 = -4.13, 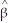 1 = 5.37,
1 = 5.37,  2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line.
2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line.
(b)Using the same spreadsheet calculations,list how the probability increases for blacks and for whites as the P/I ratio increases from 0.5 to 0.6.
(c)What is the difference in the rejection probability between blacks and whites for a P/I ratio of 0.5 and for 0.9? Why is the difference smaller for the higher value here?
(d)Table 11.2 on page 401 of your textbook lists logit regressions (column 2)with further explanatory variables.Given that you can only produce simple plots in two dimensions,how would you proceed in (a)above if there were more than a single explanatory variable?
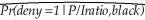 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)(a)Using a spreadsheet program such as Excel,plot the following logistic regression function with a single X,
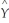 i =
i = 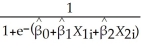 where
where 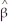 0 = -4.13,
0 = -4.13, 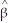 1 = 5.37,
1 = 5.37,  2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line.
2 = 1.27.Enter values for X1 in the first column starting from 0 and then increment these by 0.1 until you reach 2.0.Let X2 be 0 at first.Then enter the logistic function formula in the next column.Next allow X2 to be 1 and calculate the new values for the logistic function in the third column.Finally produce the predicted probabilities for both blacks and whites,connecting the predicted values with a line.(b)Using the same spreadsheet calculations,list how the probability increases for blacks and for whites as the P/I ratio increases from 0.5 to 0.6.
(c)What is the difference in the rejection probability between blacks and whites for a P/I ratio of 0.5 and for 0.9? Why is the difference smaller for the higher value here?
(d)Table 11.2 on page 401 of your textbook lists logit regressions (column 2)with further explanatory variables.Given that you can only produce simple plots in two dimensions,how would you proceed in (a)above if there were more than a single explanatory variable?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
32
(Requires Advanced material)Maximum likelihood estimation yields the values of the coefficients that
A)minimize the sum of squared prediction errors.
B)maximize the likelihood function.
C)come from a probability distribution and hence have to be positive.
D)are typically larger than those from OLS estimation.
A)minimize the sum of squared prediction errors.
B)maximize the likelihood function.
C)come from a probability distribution and hence have to be positive.
D)are typically larger than those from OLS estimation.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
33
Your task is to model students' choice for taking an additional economics course after the first principles course.Describe how to formulate a model based on data for a large sample of students.Outline several estimation methods and their relative advantage over other methods in tackling this problem.How would you go about interpreting the resulting output? What summary statistics should be included?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
34
Equation (11.3)in your textbook presents the regression results for the linear probability model,and equation (11.10)the results for the logit model.
a.Using a spreadsheet program such as Excel,plot the predicted probabilities for being denied a loan for both the linear probability model and the logit model if you are black.(Use a range from 0 to 1 for the P/I Ratio and allow for it to increase by increments of 0.05. )
b.Given the shortcomings of the linear probability model,do you think that it is a reasonable approximation to the logit model?
c.Repeat the exercise using predicted probabilities for whites.
a.Using a spreadsheet program such as Excel,plot the predicted probabilities for being denied a loan for both the linear probability model and the logit model if you are black.(Use a range from 0 to 1 for the P/I Ratio and allow for it to increase by increments of 0.05. )
b.Given the shortcomings of the linear probability model,do you think that it is a reasonable approximation to the logit model?
c.Repeat the exercise using predicted probabilities for whites.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
35
Sketch the regression line for the linear probability model with a single regressor.Indicate for which values of the slope and intercept the predictions will be above one and below zero.Can you rule out homoskedasticity in the error terms with certainty here?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
36
Your textbook plots the estimated regression function produced by the probit regression of deny on P/I ratio.The estimated probit regression function has a stretched "S" shape given that the coefficient on the P/I ratio is positive.Consider a probit regression function with a negative coefficient.The shape would
A)resemble an inverted "S" shape (for low values of X,the predicted probability of Y would approach 1)
B)not exist since probabilities cannot be negative
C)remain the "S" shape as with a positive slope coefficient
D)would have to be estimated with a logit function
A)resemble an inverted "S" shape (for low values of X,the predicted probability of Y would approach 1)
B)not exist since probabilities cannot be negative
C)remain the "S" shape as with a positive slope coefficient
D)would have to be estimated with a logit function

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
37
Equation (11.3)in your textbook presents the regression results for the linear probability model.
a.Using a spreadsheet program such as Excel,plot the fitted values for whites and blacks in the same graph,for P/I ratios ranging from 0 to 1 (use 0.05 increments).
b.Explain some of the strengths and shortcomings of the linear probability model using this graph.
a.Using a spreadsheet program such as Excel,plot the fitted values for whites and blacks in the same graph,for P/I ratios ranging from 0 to 1 (use 0.05 increments).
b.Explain some of the strengths and shortcomings of the linear probability model using this graph.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
38
When testing joint hypothesis,you can use
A)the F- statistic
B)the chi-squared statistic
C)either the F-statistic or the chi-square statistic
D)none of the above
A)the F- statistic
B)the chi-squared statistic
C)either the F-statistic or the chi-square statistic
D)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
39
The Report of the Presidential Commission on the Space Shuttle Challenger Accident in 1986 shows a plot of the calculated joint temperature in Fahrenheit and the number of O-rings that had some thermal distress.You collect the data for the seven flights for which thermal distress was identified before the fatal flight and produce the accompanying plot.  (a)Do you see any relationship between the temperature and the number of O-ring failures? If you fitted a linear regression line through these seven observations,do you think the slope would be positive or negative? Significantly different from zero? Do you see any problems other than the sample size in your procedure?
(a)Do you see any relationship between the temperature and the number of O-ring failures? If you fitted a linear regression line through these seven observations,do you think the slope would be positive or negative? Significantly different from zero? Do you see any problems other than the sample size in your procedure?
(b)You decide to look at all successful launches before Challenger,even those for which there were no incidents.Furthermore you simplify the problem by specifying a binary variable,which takes on the value one if there was some O-ring failure and is zero otherwise.You then fit a linear probability model with the following result,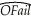 = 2.858 - 0.037 × Temperature;R2 = 0.325,SER = 0.390,
= 2.858 - 0.037 × Temperature;R2 = 0.325,SER = 0.390,
(0.496)(0.007)
where Ofail is the binary variable which is one for launches where O-rings showed some thermal distress,and Temperature is measured in degrees of Fahrenheit.The numbers in parentheses are heteroskedasticity-robust standard errors.
Interpret the equation.Why do you think that heteroskedasticity-robust standard errors were used? What is your prediction for some O-ring thermal distress when the temperature is 31°,the temperature on January 28,1986? Above which temperature do you predict values of less than zero? Below which temperature do you predict values of greater than one?
(c)To fix the problem encountered in (b),you re-estimate the relationship using a logit regression:
Pr(OFail = 1 Temperature)= F (15.297 - 0.236 × Temperature);pseudo- R2=0.297
Temperature)= F (15.297 - 0.236 × Temperature);pseudo- R2=0.297
(7.329)(0.107)
What is the meaning of the slope coefficient? Calculate the effect of a decrease in temperature from 80° to 70°,and from 60° to 50°.Why is the change in probability not constant? How does this compare to the linear probability model?
(d)You want to see how sensitive the results are to using the logit,rather than the probit estimation method.The probit regression is as follows:
Pr(OFail = 1 Temperature)= Φ(8.900 - 0.137 × Temperature);pseudo- R2=0.296
Temperature)= Φ(8.900 - 0.137 × Temperature);pseudo- R2=0.296
(3.983)(0.058)
Why is the slope coefficient in the probit so different from the logit coefficient? Calculate the effect of a decrease in temperature from 80° to 70°,and from 60° to 50° and compare the resulting changes in probability to your results in (c).What is the meaning of the pseudo- R2? What other measures of fit might you want to consider?
(e)Calculate the predicted probability for 80° and 40°,using your probit and logit estimates.Based on the relationship between the probabilities,sketch what the general relationship between the logit and probit regressions is.Does there seem to be much of a difference for values other than these extreme values?
(f)You decide to run one more regression,where the dependent variable is the actual number of incidences (NoOFail).You allow for a different functional form by choosing the inverse of the temperature,and estimate the regression by OLS.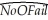 = -3.8853 + 295.545 × (1/Temperature);R2 = 0.386,SER = 0.622
= -3.8853 + 295.545 × (1/Temperature);R2 = 0.386,SER = 0.622
(1.516)(106.541)
What is your prediction for O-ring failures for the 31° temperature which was forecasted for the launch on January 28,1986? Sketch the fitted line of the regression above.
 (a)Do you see any relationship between the temperature and the number of O-ring failures? If you fitted a linear regression line through these seven observations,do you think the slope would be positive or negative? Significantly different from zero? Do you see any problems other than the sample size in your procedure?
(a)Do you see any relationship between the temperature and the number of O-ring failures? If you fitted a linear regression line through these seven observations,do you think the slope would be positive or negative? Significantly different from zero? Do you see any problems other than the sample size in your procedure?(b)You decide to look at all successful launches before Challenger,even those for which there were no incidents.Furthermore you simplify the problem by specifying a binary variable,which takes on the value one if there was some O-ring failure and is zero otherwise.You then fit a linear probability model with the following result,
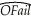 = 2.858 - 0.037 × Temperature;R2 = 0.325,SER = 0.390,
= 2.858 - 0.037 × Temperature;R2 = 0.325,SER = 0.390,(0.496)(0.007)
where Ofail is the binary variable which is one for launches where O-rings showed some thermal distress,and Temperature is measured in degrees of Fahrenheit.The numbers in parentheses are heteroskedasticity-robust standard errors.
Interpret the equation.Why do you think that heteroskedasticity-robust standard errors were used? What is your prediction for some O-ring thermal distress when the temperature is 31°,the temperature on January 28,1986? Above which temperature do you predict values of less than zero? Below which temperature do you predict values of greater than one?
(c)To fix the problem encountered in (b),you re-estimate the relationship using a logit regression:
Pr(OFail = 1
 Temperature)= F (15.297 - 0.236 × Temperature);pseudo- R2=0.297
Temperature)= F (15.297 - 0.236 × Temperature);pseudo- R2=0.297(7.329)(0.107)
What is the meaning of the slope coefficient? Calculate the effect of a decrease in temperature from 80° to 70°,and from 60° to 50°.Why is the change in probability not constant? How does this compare to the linear probability model?
(d)You want to see how sensitive the results are to using the logit,rather than the probit estimation method.The probit regression is as follows:
Pr(OFail = 1
 Temperature)= Φ(8.900 - 0.137 × Temperature);pseudo- R2=0.296
Temperature)= Φ(8.900 - 0.137 × Temperature);pseudo- R2=0.296(3.983)(0.058)
Why is the slope coefficient in the probit so different from the logit coefficient? Calculate the effect of a decrease in temperature from 80° to 70°,and from 60° to 50° and compare the resulting changes in probability to your results in (c).What is the meaning of the pseudo- R2? What other measures of fit might you want to consider?
(e)Calculate the predicted probability for 80° and 40°,using your probit and logit estimates.Based on the relationship between the probabilities,sketch what the general relationship between the logit and probit regressions is.Does there seem to be much of a difference for values other than these extreme values?
(f)You decide to run one more regression,where the dependent variable is the actual number of incidences (NoOFail).You allow for a different functional form by choosing the inverse of the temperature,and estimate the regression by OLS.
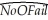 = -3.8853 + 295.545 × (1/Temperature);R2 = 0.386,SER = 0.622
= -3.8853 + 295.545 × (1/Temperature);R2 = 0.386,SER = 0.622(1.516)(106.541)
What is your prediction for O-ring failures for the 31° temperature which was forecasted for the launch on January 28,1986? Sketch the fitted line of the regression above.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
40
F-statistics computed using maximum likelihood estimators
A)cannot be used to test joint hypothesis
B)are not meaningful since the entire regression R2 concept is hard to apply in this situation
C)do not follow the standard F distribution
D)can be used to test joint hypothesis
A)cannot be used to test joint hypothesis
B)are not meaningful since the entire regression R2 concept is hard to apply in this situation
C)do not follow the standard F distribution
D)can be used to test joint hypothesis

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
41
You have a limited dependent variable (Y)and a single explanatory variable (X).You estimate the relationship using the linear probability model,a probit regression,and a logit regression.The results are as follows: 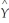 = 2.858 - 0.037 × X
= 2.858 - 0.037 × X
(0.007)
Pr(Y = 1 X)= F (15.297 - 0.236 × X)
X)= F (15.297 - 0.236 × X)
Pr(Y = 1 X)= Φ (8.900 - 0.137 × X)
X)= Φ (8.900 - 0.137 × X)
(0.058)
(a)Although you cannot compare the coefficients directly,you are told that "it can be shown" that certain relationships between the coefficients of these models hold approximately.These are for the slope: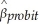 ≈ 0.625 ×
≈ 0.625 ×  ,
,  ≈ 0.25 ×
≈ 0.25 × 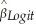 .Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
.Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
(b)For the intercept,the same conversion holds for the logit-to-probit transformation.However,for the linear probability model,there is a different conversion: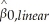 ≈ 0.25 ×
≈ 0.25 × 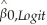 + 0.5
+ 0.5
Using the logit regression as the base,calculate a few changes in X (temperature in degrees of Fahrenheit)to see how good the approximations are.
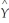 = 2.858 - 0.037 × X
= 2.858 - 0.037 × X(0.007)
Pr(Y = 1
 X)= F (15.297 - 0.236 × X)
X)= F (15.297 - 0.236 × X)Pr(Y = 1
 X)= Φ (8.900 - 0.137 × X)
X)= Φ (8.900 - 0.137 × X)(0.058)
(a)Although you cannot compare the coefficients directly,you are told that "it can be shown" that certain relationships between the coefficients of these models hold approximately.These are for the slope:
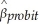 ≈ 0.625 ×
≈ 0.625 ×  ,
,  ≈ 0.25 ×
≈ 0.25 × 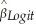 .Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?
.Take the logit result above as a base and calculate the slope coefficients for the linear probability model and the probit regression.Are these values close?(b)For the intercept,the same conversion holds for the logit-to-probit transformation.However,for the linear probability model,there is a different conversion:
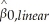 ≈ 0.25 ×
≈ 0.25 × 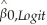 + 0.5
+ 0.5Using the logit regression as the base,calculate a few changes in X (temperature in degrees of Fahrenheit)to see how good the approximations are.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
42
(Requires Appendix material)Briefly describe the difference between the following models: censored and truncated regression model,count data,ordered responses,and discrete choice data.Try to be specific in terms of describing the data involved.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
43
Consider the following probit regression
Pr(Y = 1 X)= Φ(8.9 - 0.14 × X)
X)= Φ(8.9 - 0.14 × X)
Calculate the change in probability for X increasing by 10 for X = 40 and X = 60.Why is there such a large difference in the change in probabilities?
Pr(Y = 1
 X)= Φ(8.9 - 0.14 × X)
X)= Φ(8.9 - 0.14 × X)Calculate the change in probability for X increasing by 10 for X = 40 and X = 60.Why is there such a large difference in the change in probabilities?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
44
(Requires Appendix material and Calculus)The logarithm of the likelihood function (L)for estimating the population mean and variance for an i.i.d.normal sample is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum):
L = -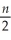 log(2πσ2)-
log(2πσ2)- 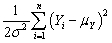 Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?
Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?
L = -
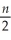 log(2πσ2)-
log(2πσ2)- 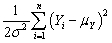 Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?
Derive the maximum likelihood estimator for the mean and the variance.How do they differ,if at all,from the OLS estimator? Given that the OLS estimators are unbiased,what can you say about the maximum likelihood estimators here? Is the estimator for the variance consistent?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
45
Earnings equations establish a relationship between an individual's earnings and its determinants such as years of education,tenure with an employer,IQ of the individual,professional choice,region within the country the individual is living in,etc.In addition,binary variables are often added to test for "discrimination" against certain sub-groups of the labor force such as blacks,females,etc.Compare this approach to the study in the textbook,which also investigates evidence on discrimination.Explain the fundamental differences in both approaches using equations and mathematical specifications whenever possible.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
46
The population logit model of the binary dependent variable Y with a single regressor is
Pr(Y=1 X1)=
X1)= 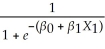 .
.
Logistic functions also play a role in econometrics when the dependent variable is not a binary variable.For example,the demand for televisions sets per household may be a function of income,but there is a saturation or satiation level per household,so that a linear specification may not be appropriate.Given the regression model
Yi =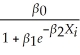 + ui,
+ ui,
sketch the regression line.How would you go about estimating the coefficients?
Pr(Y=1
 X1)=
X1)= 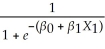 .
.Logistic functions also play a role in econometrics when the dependent variable is not a binary variable.For example,the demand for televisions sets per household may be a function of income,but there is a saturation or satiation level per household,so that a linear specification may not be appropriate.Given the regression model
Yi =
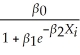 + ui,
+ ui,sketch the regression line.How would you go about estimating the coefficients?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
47
Besides maximum likelihood estimation of the logit and probit model,your textbook mentions that the model can also be estimated by nonlinear least squares.Construct the sum of squared prediction mistakes and suggest how computer algorithms go about finding the coefficient values that minimize the function.You may want to use an analogy where you place yourself into a mountain range at night with a flashlight shining at your feet.Your task is to find the lowest point in the valley.You have two choices to make: the direction you are walking in and the step length.Describe how you will proceed to find the bottom of the valley.Once you find the lowest point,is there any guarantee that this is the lowest point of all valleys? What should you do to assure this?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
48
The estimated logit regression in your textbook is 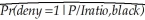 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)
Using a spreadsheet program,such as Excel,generate a table with predicted probabilities for both whites and blacks using P/I Ratio values between 0 and 1 and increments of 0.05.
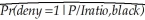 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)Using a spreadsheet program,such as Excel,generate a table with predicted probabilities for both whites and blacks using P/I Ratio values between 0 and 1 and increments of 0.05.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
49
The estimated logit regression in your textbook is 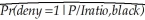 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)
Is there a meaningful interpretation to the slope for the P/I Ratio? Calculate the increase of a rejection probability for both blacks and whites as the P/I Ratio increases from 0.1 to 0.2.Repeat the exercise for an increase from 0.65 to 0.75.Why is the increase in the probability higher for blacks at the smaller value of the P/I Ratio but higher for whites at the larger P/I Ratio?
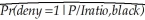 = F(-4.13 + 5.37 P/Iratio + 1.27 black)
= F(-4.13 + 5.37 P/Iratio + 1.27 black)Is there a meaningful interpretation to the slope for the P/I Ratio? Calculate the increase of a rejection probability for both blacks and whites as the P/I Ratio increases from 0.1 to 0.2.Repeat the exercise for an increase from 0.65 to 0.75.Why is the increase in the probability higher for blacks at the smaller value of the P/I Ratio but higher for whites at the larger P/I Ratio?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck
50
(Requires Appendix material and Calculus)The log of the likelihood function (L)for the simple regression model with i.i.d.normal errors is as follows (note that taking the logarithm of the likelihood function simplifies maximization.It is a monotonic transformation of the likelihood function,meaning that this transformation does not affect the choice of maximum):
L = -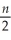 log(2π)-
log(2π)-  log σ2 -
log σ2 - 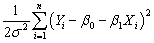 Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here.
Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here.
L = -
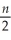 log(2π)-
log(2π)-  log σ2 -
log σ2 - 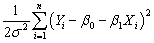 Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here.
Derive the maximum likelihood estimator for the slope and intercept.What general properties do these estimators have? Explain intuitively why the OLS estimator is identical to the maximum likelihood estimator here.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 50 في هذه المجموعة.
فتح الحزمة
k this deck








