Deck 2: Review of Probability
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/71
العب
ملء الشاشة (f)
Deck 2: Review of Probability
1
Two variables are uncorrelated in all of the cases below,with the exception of
A)being independent.
B)having a zero covariance.
C)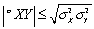
D)E(Y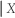 )= 0.
)= 0.
A)being independent.
B)having a zero covariance.
C)
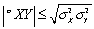
D)E(Y
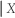 )= 0.
)= 0.C
2
For a normal distribution,the skewness and kurtosis measures are as follows:
A)1.96 and 4
B)0 and 0
C)0 and 3
D)1 and 2
A)1.96 and 4
B)0 and 0
C)0 and 3
D)1 and 2
C
3
The Student t distribution is
A)the distribution of the sum of m squared independent standard normal random variables.
B)the distribution of a random variable with a chi-squared distribution with m degrees of freedom,divided by m.
C)always well approximated by the standard normal distribution.
D)the distribution of the ratio of a standard normal random variable,divided by the square root of an independently distributed chi-squared random variable with m degrees of freedom divided by m.
A)the distribution of the sum of m squared independent standard normal random variables.
B)the distribution of a random variable with a chi-squared distribution with m degrees of freedom,divided by m.
C)always well approximated by the standard normal distribution.
D)the distribution of the ratio of a standard normal random variable,divided by the square root of an independently distributed chi-squared random variable with m degrees of freedom divided by m.
D
4
When there are ∞ degrees of freedom,the t∞ distribution
A)can no longer be calculated.
B)equals the standard normal distribution.
C)has a bell shape similar to that of the normal distribution,but with "fatter" tails.
D)equals the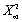 distribution.
distribution.
A)can no longer be calculated.
B)equals the standard normal distribution.
C)has a bell shape similar to that of the normal distribution,but with "fatter" tails.
D)equals the
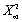 distribution.
distribution.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
5
The skewness of the distribution of a random variable Y is defined as follows:
A)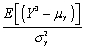
B)
C)
D)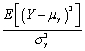
A)
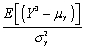
B)

C)

D)
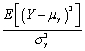

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
6
The kurtosis of a distribution is defined as follows:
A)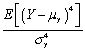
B)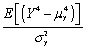
C)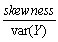
D)E[(Y -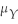 )4)
)4)
A)
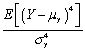
B)
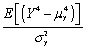
C)
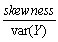
D)E[(Y -
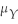 )4)
)4)
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
7
The skewness is most likely positive for one of the following distributions:
A)The grade distribution at your college or university.
B)The U.S.income distribution.
C)SAT scores in English.
D)The height of 18 year old females in the U.S.
A)The grade distribution at your college or university.
B)The U.S.income distribution.
C)SAT scores in English.
D)The height of 18 year old females in the U.S.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
8
The correlation between X and Y
A)cannot be negative since variances are always positive.
B)is the covariance squared.
C)can be calculated by dividing the covariance between X and Y by the product of the two standard deviations.
D)is given by corr(X,Y)=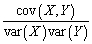 .
.
A)cannot be negative since variances are always positive.
B)is the covariance squared.
C)can be calculated by dividing the covariance between X and Y by the product of the two standard deviations.
D)is given by corr(X,Y)=
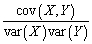 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
9
The conditional distribution of Y given X = x,Pr(Y = y  =x),is
=x),is
A)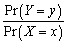 .
.
B)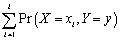
C)
D)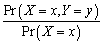 .
.
 =x),is
=x),isA)
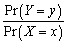 .
.B)
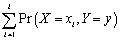
C)

D)
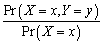 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
10
The probability of an outcome
A)is the number of times that the outcome occurs in the long run.
B)equals M × N,where M is the number of occurrences and N is the population size.
C)is the proportion of times that the outcome occurs in the long run.
D)equals the sample mean divided by the sample standard deviation.
A)is the number of times that the outcome occurs in the long run.
B)equals M × N,where M is the number of occurrences and N is the population size.
C)is the proportion of times that the outcome occurs in the long run.
D)equals the sample mean divided by the sample standard deviation.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
11
If variables with a multivariate normal distribution have covariances that equal zero,then
A)the correlation will most often be zero,but does not have to be.
B)the variables are independent.
C)you should use the χ2 distribution to calculate probabilities.
D)the marginal distribution of each of the variables is no longer normal.
A)the correlation will most often be zero,but does not have to be.
B)the variables are independent.
C)you should use the χ2 distribution to calculate probabilities.
D)the marginal distribution of each of the variables is no longer normal.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
12
Let Y be a random variable.Then var(Y)equals
A) .
.
B)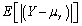 .
.
C) .
.
D)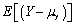 .
.
A)
 .
.B)
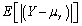 .
.C)
 .
.D)
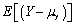 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
13
Assume that Y is normally distributed N(μ,σ2).To find Pr(c1 ≤ Y ≤ c2),where c1 < c2 and di = 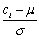 ,you need to calculate Pr(d1 ≤ Z ≤ d2)=
,you need to calculate Pr(d1 ≤ Z ≤ d2)=
A)Φ(d2)- Φ(d1)
B)Φ(1.96)- Φ(1.96)
C)Φ(d2)- (1 - Φ(d1))
D)1 - (Φ(d2)- Φ(d1))
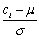 ,you need to calculate Pr(d1 ≤ Z ≤ d2)=
,you need to calculate Pr(d1 ≤ Z ≤ d2)=A)Φ(d2)- Φ(d1)
B)Φ(1.96)- Φ(1.96)
C)Φ(d2)- (1 - Φ(d1))
D)1 - (Φ(d2)- Φ(d1))

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
14
The expected value of a discrete random variable
A)is the outcome that is most likely to occur.
B)can be found by determining the 50% value in the c.d.f.
C)equals the population median.
D)is computed as a weighted average of the possible outcome of that random variable,where the weights are the probabilities of that outcome.
A)is the outcome that is most likely to occur.
B)can be found by determining the 50% value in the c.d.f.
C)equals the population median.
D)is computed as a weighted average of the possible outcome of that random variable,where the weights are the probabilities of that outcome.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
15
The conditional expectation of Y given X,E(Y 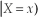 ,is calculated as follows:
,is calculated as follows:
A)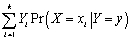
B)E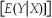
C)
D)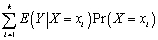
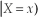 ,is calculated as follows:
,is calculated as follows:A)
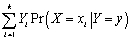
B)E
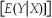
C)

D)
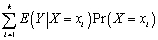

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
16
var(aX + bY)=
A)
B)
C)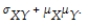
D)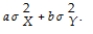
A)

B)

C)
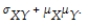
D)
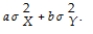

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
17
Two random variables X and Y are independently distributed if all of the following conditions hold,with the exception of
A)Pr(Y = y![<strong>Two random variables X and Y are independently distributed if all of the following conditions hold,with the exception of</strong> A)Pr(Y = y = x)= Pr(Y = y). B)knowing the value of one of the variables provides no information about the other. C)if the conditional distribution of Y given X equals the marginal distribution of Y. D)E(Y)= E[E(Y )].](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd42_a5cf_896a_3fb6e11c038d_TB2833_11.jpg) = x)= Pr(Y = y).
= x)= Pr(Y = y).
B)knowing the value of one of the variables provides no information about the other.
C)if the conditional distribution of Y given X equals the marginal distribution of Y.
D)E(Y)= E[E(Y![<strong>Two random variables X and Y are independently distributed if all of the following conditions hold,with the exception of</strong> A)Pr(Y = y = x)= Pr(Y = y). B)knowing the value of one of the variables provides no information about the other. C)if the conditional distribution of Y given X equals the marginal distribution of Y. D)E(Y)= E[E(Y )].](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd42_cce0_896a_d997fd196c77_TB2833_11.jpg) )].
)].
A)Pr(Y = y
![<strong>Two random variables X and Y are independently distributed if all of the following conditions hold,with the exception of</strong> A)Pr(Y = y = x)= Pr(Y = y). B)knowing the value of one of the variables provides no information about the other. C)if the conditional distribution of Y given X equals the marginal distribution of Y. D)E(Y)= E[E(Y )].](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd42_a5cf_896a_3fb6e11c038d_TB2833_11.jpg) = x)= Pr(Y = y).
= x)= Pr(Y = y).B)knowing the value of one of the variables provides no information about the other.
C)if the conditional distribution of Y given X equals the marginal distribution of Y.
D)E(Y)= E[E(Y
![<strong>Two random variables X and Y are independently distributed if all of the following conditions hold,with the exception of</strong> A)Pr(Y = y = x)= Pr(Y = y). B)knowing the value of one of the variables provides no information about the other. C)if the conditional distribution of Y given X equals the marginal distribution of Y. D)E(Y)= E[E(Y )].](https://d2lvgg3v3hfg70.cloudfront.net/TB2833/11eab146_bd42_cce0_896a_d997fd196c77_TB2833_11.jpg) )].
)].
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
18
The cumulative probability distribution shows the probability
A)that a random variable is less than or equal to a particular value.
B)of two or more events occurring at once.
C)of all possible events occurring.
D)that a random variable takes on a particular value given that another event has happened.
A)that a random variable is less than or equal to a particular value.
B)of two or more events occurring at once.
C)of all possible events occurring.
D)that a random variable takes on a particular value given that another event has happened.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
19
Assume that Y is normally distributed N(μ,σ2).Moving from the mean (μ)1.96 standard deviations to the left and 1.96 standard deviations to the right,then the area under the normal p.d.f.is
A)0.67
B)0.05
C)0.95
D)0.33
A)0.67
B)0.05
C)0.95
D)0.33

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
20
To standardize a variable you
A)subtract its mean and divide by its standard deviation.
B)integrate the area below two points under the normal distribution.
C)add and subtract 1.96 times the standard deviation to the variable.
D)divide it by its standard deviation,as long as its mean is 1.
A)subtract its mean and divide by its standard deviation.
B)integrate the area below two points under the normal distribution.
C)add and subtract 1.96 times the standard deviation to the variable.
D)divide it by its standard deviation,as long as its mean is 1.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
21
The covariance inequality states that
A)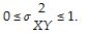
B)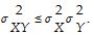
C)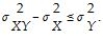
D)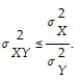
A)
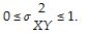
B)
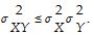
C)
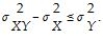
D)
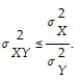

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
22
The mean and variance of a Bernoille random variable are given as
A)cannot be calculated
B)np and np(1-p)
C)p and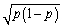
D)p and (1- p)
A)cannot be calculated
B)np and np(1-p)
C)p and
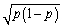
D)p and (1- p)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
23
You have read about the so-called catch-up theory by economic historians,whereby nations that are further behind in per capita income grow faster subsequently.If this is true systematically,then eventually laggards will reach the leader.To put the theory to the test,you collect data on relative (to the United States)per capita income for two years,1960 and 1990,for 24 OECD countries.You think of these countries as a population you want to describe,rather than a sample from which you want to infer behavior of a larger population.The relevant data for this question is as follows: 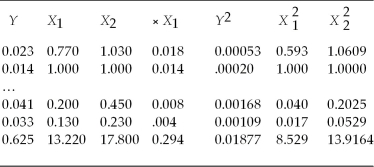 where X1 and X2 are per capita income relative to the United States in 1960 and 1990 respectively,and Y is the average annual growth rate in X over the 1960-1990 period.Numbers in the last row represent sums of the columns above.
where X1 and X2 are per capita income relative to the United States in 1960 and 1990 respectively,and Y is the average annual growth rate in X over the 1960-1990 period.Numbers in the last row represent sums of the columns above.
(a)Calculate the variance and standard deviation of X1 and X2.For a catch-up effect to be present,what relationship must the two standard deviations show? Is this the case here?
(b)Calculate the correlation between Y and .What sign must the correlation coefficient have for there to be evidence of a catch-up effect? Explain.
 where X1 and X2 are per capita income relative to the United States in 1960 and 1990 respectively,and Y is the average annual growth rate in X over the 1960-1990 period.Numbers in the last row represent sums of the columns above.
where X1 and X2 are per capita income relative to the United States in 1960 and 1990 respectively,and Y is the average annual growth rate in X over the 1960-1990 period.Numbers in the last row represent sums of the columns above.(a)Calculate the variance and standard deviation of X1 and X2.For a catch-up effect to be present,what relationship must the two standard deviations show? Is this the case here?
(b)Calculate the correlation between Y and .What sign must the correlation coefficient have for there to be evidence of a catch-up effect? Explain.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
24
Math and verbal SAT scores are each distributed normally with N (500,10000).
(a)What fraction of students scores above 750? Above 600? Between 420 and 530? Below 480? Above 530?
(b)If the math and verbal scores were independently distributed,which is not the case,then what would be the distribution of the overall SAT score? Find its mean and variance.
(c)Next,assume that the correlation coefficient between the math and verbal scores is 0.75.Find the mean and variance of the resulting distribution.
(d)Finally,assume that you had chosen 25 students at random who had taken the SAT exam.Derive the distribution for their average math SAT score.What is the probability that this average is above 530? Why is this so much smaller than your answer in (a)?
(a)What fraction of students scores above 750? Above 600? Between 420 and 530? Below 480? Above 530?
(b)If the math and verbal scores were independently distributed,which is not the case,then what would be the distribution of the overall SAT score? Find its mean and variance.
(c)Next,assume that the correlation coefficient between the math and verbal scores is 0.75.Find the mean and variance of the resulting distribution.
(d)Finally,assume that you had chosen 25 students at random who had taken the SAT exam.Derive the distribution for their average math SAT score.What is the probability that this average is above 530? Why is this so much smaller than your answer in (a)?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
25
Think of the situation of rolling two dice and let M denote the sum of the number of dots on the two dice.(So M is a number between 1 and 12. )
(a)In a table,list all of the possible outcomes for the random variable M together with its probability distribution and cumulative probability distribution.Sketch both distributions.
(b)Calculate the expected value and the standard deviation for M.
(c)Looking at the sketch of the probability distribution,you notice that it resembles a normal distribution.Should you be able to use the standard normal distribution to calculate probabilities of events? Why or why not?
(a)In a table,list all of the possible outcomes for the random variable M together with its probability distribution and cumulative probability distribution.Sketch both distributions.
(b)Calculate the expected value and the standard deviation for M.
(c)Looking at the sketch of the probability distribution,you notice that it resembles a normal distribution.Should you be able to use the standard normal distribution to calculate probabilities of events? Why or why not?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
26
Probabilities and relative frequencies are related in that the probability of an outcome is the proportion of the time that the outcome occurs in the long run.Hence concepts of joint,marginal,and conditional probability distributions stem from related concepts of frequency distributions.
You are interested in investigating the relationship between the age of heads of households and weekly earnings of households.The accompanying data gives the number of occurrences grouped by age and income.You collect data from 1,744 individuals and think of these individuals as a population that you want to describe,rather than a sample from which you want to infer behavior of a larger population.After sorting the data,you generate the accompanying table:
Joint Absolute Frequencies of Age and Income,1,744 Households
Age of head of household
X1 X2 X3 X4 X5 The median of the income group of $800 and above is $1,050.
The median of the income group of $800 and above is $1,050.
(a)Calculate the joint relative frequencies and the marginal relative frequencies.Interpret one of each of these.Sketch the cumulative income distribution.
(b)Calculate the conditional relative income frequencies for the two age categories 16-under 20,and 45-under 65.Calculate the mean household income for both age categories.
(c)If household income and age of head of household were independently distributed,what would you expect these two conditional relative income distributions to look like? Are they similar here?
(d)Your textbook has given you a primary definition of independence that does not involve conditional relative frequency distributions.What is that definition? Do you think that age and income are independent here,using this definition?
You are interested in investigating the relationship between the age of heads of households and weekly earnings of households.The accompanying data gives the number of occurrences grouped by age and income.You collect data from 1,744 individuals and think of these individuals as a population that you want to describe,rather than a sample from which you want to infer behavior of a larger population.After sorting the data,you generate the accompanying table:
Joint Absolute Frequencies of Age and Income,1,744 Households
Age of head of household
X1 X2 X3 X4 X5
 The median of the income group of $800 and above is $1,050.
The median of the income group of $800 and above is $1,050.(a)Calculate the joint relative frequencies and the marginal relative frequencies.Interpret one of each of these.Sketch the cumulative income distribution.
(b)Calculate the conditional relative income frequencies for the two age categories 16-under 20,and 45-under 65.Calculate the mean household income for both age categories.
(c)If household income and age of head of household were independently distributed,what would you expect these two conditional relative income distributions to look like? Are they similar here?
(d)Your textbook has given you a primary definition of independence that does not involve conditional relative frequency distributions.What is that definition? Do you think that age and income are independent here,using this definition?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
27
To infer the political tendencies of the students at your college/university,you sample 150 of them.Only one of the following is a simple random sample: You
A)make sure that the proportion of minorities are the same in your sample as in the entire student body.
B)call every fiftieth person in the student directory at 9 a.m.If the person does not answer the phone,you pick the next name listed,and so on.
C)go to the main dining hall on campus and interview students randomly there.
D)have your statistical package generate 150 random numbers in the range from 1 to the total number of students in your academic institution,and then choose the corresponding names in the student telephone directory.
A)make sure that the proportion of minorities are the same in your sample as in the entire student body.
B)call every fiftieth person in the student directory at 9 a.m.If the person does not answer the phone,you pick the next name listed,and so on.
C)go to the main dining hall on campus and interview students randomly there.
D)have your statistical package generate 150 random numbers in the range from 1 to the total number of students in your academic institution,and then choose the corresponding names in the student telephone directory.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
28
Consistency for the sample average 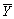 can be defined as follows,with the exception of
can be defined as follows,with the exception of
A)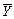 converges in probability to
converges in probability to
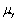 .
.
B)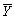 has the smallest variance of all estimators.
has the smallest variance of all estimators.
C)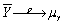 .
.
D)the probability of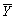 being in the range
being in the range
 ± c becomes arbitrarily close to one as n increases for any constant c > 0.
± c becomes arbitrarily close to one as n increases for any constant c > 0.
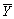 can be defined as follows,with the exception of
can be defined as follows,with the exception ofA)
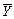 converges in probability to
converges in probability to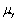 .
.B)
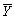 has the smallest variance of all estimators.
has the smallest variance of all estimators.C)
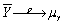 .
.D)the probability of
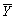 being in the range
being in the range ± c becomes arbitrarily close to one as n increases for any constant c > 0.
± c becomes arbitrarily close to one as n increases for any constant c > 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
29
The sample average is a random variable and
A)is a single number and as a result cannot have a distribution.
B)has a probability distribution called its sampling distribution.
C)has a probability distribution called the standard normal distribution.
D)has a probability distribution that is the same as for the Y1,... ,Yn i.i.d.variables.
A)is a single number and as a result cannot have a distribution.
B)has a probability distribution called its sampling distribution.
C)has a probability distribution called the standard normal distribution.
D)has a probability distribution that is the same as for the Y1,... ,Yn i.i.d.variables.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
30
The variance of 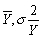 ,is given by the following formula:
,is given by the following formula:
A)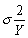 .
.
B)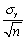 .
.
C)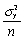 .
.
D) .
.
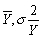 ,is given by the following formula:
,is given by the following formula:A)
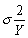 .
.B)
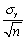 .
.C)
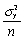 .
.D)
 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
31
Assume that you assign the following subjective probabilities for your final grade in your econometrics course (the standard GPA scale of 4 = A to 0 = F applies):  The expected value is:
The expected value is:
A)3.0
B)3.5
C)2.78
D)3.25
 The expected value is:
The expected value is:A)3.0
B)3.5
C)2.78
D)3.25

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
32
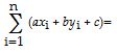
A)
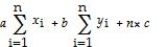
B)

C)
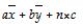
D)
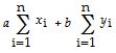

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
33
In econometrics,we typically do not rely on exact or finite sample distributions because
A)we have approximately an infinite number of observations (think of re-sampling).
B)variables typically are normally distributed.
C)the covariances of Yi,Yj are typically not zero.
D)asymptotic distributions can be counted on to provide good approximations to the exact sampling distribution (given the number of observations available in most cases).
A)we have approximately an infinite number of observations (think of re-sampling).
B)variables typically are normally distributed.
C)the covariances of Yi,Yj are typically not zero.
D)asymptotic distributions can be counted on to provide good approximations to the exact sampling distribution (given the number of observations available in most cases).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
34
The central limit theorem states that
A)the sampling distribution of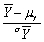 is approximately normal.
is approximately normal.
B)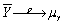 .
.
C)the probability that is in the range
is in the range
 ± c becomes arbitrarily close to one as n increases for any constant c > 0.
± c becomes arbitrarily close to one as n increases for any constant c > 0.
D)the t distribution converges to the F distribution for approximately n > 30.
A)the sampling distribution of
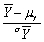 is approximately normal.
is approximately normal.B)
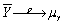 .
.C)the probability that
 is in the range
is in the range ± c becomes arbitrarily close to one as n increases for any constant c > 0.
± c becomes arbitrarily close to one as n increases for any constant c > 0.D)the t distribution converges to the F distribution for approximately n > 30.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
35
Consider the following linear transformation of a random variable y = 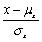 where μx is the mean of x and σx is the standard deviation.Then the expected value and the standard deviation of Y are given as
where μx is the mean of x and σx is the standard deviation.Then the expected value and the standard deviation of Y are given as
A)0 and 1
B)1 and 1
C)Cannot be computed because Y is not a linear function of X
D)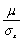 and σx
and σx
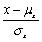 where μx is the mean of x and σx is the standard deviation.Then the expected value and the standard deviation of Y are given as
where μx is the mean of x and σx is the standard deviation.Then the expected value and the standard deviation of Y are given asA)0 and 1
B)1 and 1
C)Cannot be computed because Y is not a linear function of X
D)
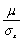 and σx
and σx
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
36
The following problem is frequently encountered in the case of a rare disease,say AIDS,when determining the probability of actually having the disease after testing positively for HIV.(This is often known as the accuracy of the test given that you have the disease. )Let us set up the problem as follows: Y = 0 if you tested negative using the ELISA test for HIV,Y = 1 if you tested positive;X = 1 if you have HIV,X = 0 if you do not have HIV.Assume that 0.1 percent of the population has HIV and that the accuracy of the test is 0.95 in both cases of (i)testing positive when you have HIV,and (ii)testing negative when you do not have HIV.(The actual ELISA test is actually 99.7 percent accurate when you have HIV,and 98.5 percent accurate when you do not have HIV. )
(a)Assuming arbitrarily a population of 10,000,000 people,use the accompanying table to first enter the column totals.
 (b)Use the conditional probabilities to fill in the joint absolute frequencies.
(b)Use the conditional probabilities to fill in the joint absolute frequencies.
(c)Fill in the marginal absolute frequencies for testing positive and negative.Determine the conditional probability of having HIV when you have tested positive.Explain this surprising result.
(d)The previous problem is an application of Bayes' theorem,which converts Pr(Y = y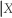 = x)into Pr(X = x
= x)into Pr(X = x  = y).Can you think of other examples where Pr(Y = y
= y).Can you think of other examples where Pr(Y = y 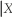 = x)≠ Pr(X = x
= x)≠ Pr(X = x 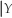 = y)?
= y)?
(a)Assuming arbitrarily a population of 10,000,000 people,use the accompanying table to first enter the column totals.
 (b)Use the conditional probabilities to fill in the joint absolute frequencies.
(b)Use the conditional probabilities to fill in the joint absolute frequencies.(c)Fill in the marginal absolute frequencies for testing positive and negative.Determine the conditional probability of having HIV when you have tested positive.Explain this surprising result.
(d)The previous problem is an application of Bayes' theorem,which converts Pr(Y = y
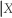 = x)into Pr(X = x
= x)into Pr(X = x  = y).Can you think of other examples where Pr(Y = y
= y).Can you think of other examples where Pr(Y = y 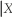 = x)≠ Pr(X = x
= x)≠ Pr(X = x 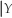 = y)?
= y)?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
37
The central limit theorem
A)states conditions under which a variable involving the sum of Y1,... ,Yn i.i.d.variables becomes the standard normal distribution.
B)postulates that the sample mean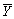 is a consistent estimator of the population mean
is a consistent estimator of the population mean
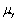 .
.
C)only holds in the presence of the law of large numbers.
D)states conditions under which a variable involving the sum of Y1,... ,Yn i.i.d.variables becomes the Student t distribution.
A)states conditions under which a variable involving the sum of Y1,... ,Yn i.i.d.variables becomes the standard normal distribution.
B)postulates that the sample mean
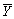 is a consistent estimator of the population mean
is a consistent estimator of the population mean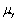 .
.C)only holds in the presence of the law of large numbers.
D)states conditions under which a variable involving the sum of Y1,... ,Yn i.i.d.variables becomes the Student t distribution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
38
The mean of the sample average  ,
, 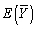 ,is
,is
A)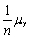 .
.
B)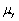 .
.
C)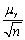 .
.
D)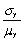 for n > 30.
for n > 30.
 ,
, 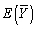 ,is
,isA)
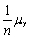 .
.B)
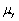 .
.C)
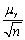 .
.D)
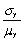 for n > 30.
for n > 30.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
39
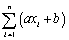
A)n × a ×
 + n × b
+ n × bB)n(a + b)
C)
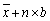
D)
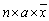

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
40
What is the probability of the following outcomes?
(a)Pr(M = 7)
(b)Pr(M = 2 or M = 10)
(c)Pr(M = 4 or M ≠ 4)
(d)Pr(M = 6 and M = 9)
(e)Pr(M < 8)
(f)Pr(M = 6 or M > 10)
(a)Pr(M = 7)
(b)Pr(M = 2 or M = 10)
(c)Pr(M = 4 or M ≠ 4)
(d)Pr(M = 6 and M = 9)
(e)Pr(M < 8)
(f)Pr(M = 6 or M > 10)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
41
There are frequently situations where you have information on the conditional distribution of Y given X,but are interested in the conditional distribution of X given Y.Recalling Pr(Y = y  = x)=
= x)=  ,derive a relationship between Pr(X = x
,derive a relationship between Pr(X = x 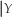 = y)and Pr(Y = y
= y)and Pr(Y = y 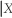 = x).This is called Bayes' theorem.
= x).This is called Bayes' theorem.
 = x)=
= x)=  ,derive a relationship between Pr(X = x
,derive a relationship between Pr(X = x 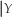 = y)and Pr(Y = y
= y)and Pr(Y = y 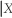 = x).This is called Bayes' theorem.
= x).This is called Bayes' theorem.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
42
Two random variables are independently distributed if their joint distribution is the product of their marginal distributions.It is intuitively easier to understand that two random variables are independently distributed if all conditional distributions of Y given X are equal.Derive one of the two conditions from the other.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
43
Think of an example involving five possible quantitative outcomes of a discrete random variable and attach a probability to each one of these outcomes.Display the outcomes,probability distribution,and cumulative probability distribution in a table.Sketch both the probability distribution and the cumulative probability distribution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
44
Calculate the following probabilities using the standard normal distribution.Sketch the probability distribution in each case,shading in the area of the calculated probability.
(a)Pr(Z < 0.0)
(b)Pr(Z ≤ 1.0)
(c)Pr(Z > 1.96)
(d)Pr(Z < -2.0)
(e)Pr(Z > 1.645)
(f)Pr(Z > -1.645)
(g)Pr(-1.96 < Z < 1.96)
(i. )Pr(Z > z)= 0.10;find z.
(j. )Pr(Z < -z or Z > z)= 0.05;find z.
(a)Pr(Z < 0.0)
(b)Pr(Z ≤ 1.0)
(c)Pr(Z > 1.96)
(d)Pr(Z < -2.0)
(e)Pr(Z > 1.645)
(f)Pr(Z > -1.645)
(g)Pr(-1.96 < Z < 1.96)
(i. )Pr(Z > z)= 0.10;find z.
(j. )Pr(Z < -z or Z > z)= 0.05;find z.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
45
The height of male students at your college/university is normally distributed with a mean of 70 inches and a standard deviation of 3.5 inches.If you had a list of telephone numbers for male students for the purpose of conducting a survey,what would be the probability of randomly calling one of these students whose height is
(a)taller than 6'0"?
(b)between 5'3" and 6'5"?
(c)shorter than 5'7",the mean height of female students?
(d)shorter than 5'0"?
(e)taller than Shaquille O'Neal,the center of the Boston Celtics,who is 7'1" tall?
Compare this to the probability of a woman being pregnant for 10 months (300 days),where days of pregnancy is normally distributed with a mean of 266 days and a standard deviation of 16 days.
(a)taller than 6'0"?
(b)between 5'3" and 6'5"?
(c)shorter than 5'7",the mean height of female students?
(d)shorter than 5'0"?
(e)taller than Shaquille O'Neal,the center of the Boston Celtics,who is 7'1" tall?
Compare this to the probability of a woman being pregnant for 10 months (300 days),where days of pregnancy is normally distributed with a mean of 266 days and a standard deviation of 16 days.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
46
The expectations augmented Phillips curve postulates
△p = π - f (u - ),
),
where △p is the actual inflation rate,π is the expected inflation rate,and u is the unemployment rate,with "-" indicating equilibrium (the NAIRU - Non-Accelerating Inflation Rate of Unemployment).Under the assumption of static expectations (π = △p-1),i.e. ,that you expect this period's inflation rate to hold for the next period ("the sun shines today,it will shine tomorrow"),then the prediction is that inflation will accelerate if the unemployment rate is below its equilibrium level.The accompanying table below displays information on accelerating annual inflation and unemployment rate differences from the equilibrium rate (cyclical unemployment),where the latter is approximated by a five-year moving average.You think of this data as a population which you want to describe,rather than a sample from which you want to infer behavior of a larger population.The data is collected from United States quarterly data for the period 1964:1 to 1995:4.
Joint Distribution of Accelerating Inflation and Cyclical Unemployment,
1964:1-1995:4
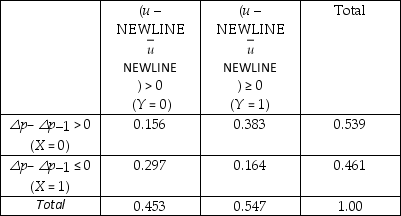 (a)Compute E(Y)and E(X),and interpret both numbers.
(a)Compute E(Y)and E(X),and interpret both numbers.
(b)Calculate E(Y = 1)and E(Y
= 1)and E(Y 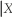 = 0).If there was independence between cyclical unemployment and acceleration in the inflation rate,what would you expect the relationship between the two expected values to be? Given that the two means are different,is this sufficient to assume that the two variables are independent?
= 0).If there was independence between cyclical unemployment and acceleration in the inflation rate,what would you expect the relationship between the two expected values to be? Given that the two means are different,is this sufficient to assume that the two variables are independent?
(c)What is the probability of inflation to increase if there is positive cyclical unemployment? Negative cyclical unemployment?
(d)You randomly select one of the 59 quarters when there was positive cyclical unemployment ((u - )> 0).What is the probability there was decelerating inflation during that quarter?
)> 0).What is the probability there was decelerating inflation during that quarter?
△p = π - f (u -
 ),
),where △p is the actual inflation rate,π is the expected inflation rate,and u is the unemployment rate,with "-" indicating equilibrium (the NAIRU - Non-Accelerating Inflation Rate of Unemployment).Under the assumption of static expectations (π = △p-1),i.e. ,that you expect this period's inflation rate to hold for the next period ("the sun shines today,it will shine tomorrow"),then the prediction is that inflation will accelerate if the unemployment rate is below its equilibrium level.The accompanying table below displays information on accelerating annual inflation and unemployment rate differences from the equilibrium rate (cyclical unemployment),where the latter is approximated by a five-year moving average.You think of this data as a population which you want to describe,rather than a sample from which you want to infer behavior of a larger population.The data is collected from United States quarterly data for the period 1964:1 to 1995:4.
Joint Distribution of Accelerating Inflation and Cyclical Unemployment,
1964:1-1995:4
 (a)Compute E(Y)and E(X),and interpret both numbers.
(a)Compute E(Y)and E(X),and interpret both numbers.(b)Calculate E(Y
 = 1)and E(Y
= 1)and E(Y 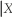 = 0).If there was independence between cyclical unemployment and acceleration in the inflation rate,what would you expect the relationship between the two expected values to be? Given that the two means are different,is this sufficient to assume that the two variables are independent?
= 0).If there was independence between cyclical unemployment and acceleration in the inflation rate,what would you expect the relationship between the two expected values to be? Given that the two means are different,is this sufficient to assume that the two variables are independent?(c)What is the probability of inflation to increase if there is positive cyclical unemployment? Negative cyclical unemployment?
(d)You randomly select one of the 59 quarters when there was positive cyclical unemployment ((u -
 )> 0).What is the probability there was decelerating inflation during that quarter?
)> 0).What is the probability there was decelerating inflation during that quarter?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
47
A few years ago the news magazine The Economist listed some of the stranger explanations used in the past to predict presidential election outcomes.These included whether or not the hemlines of women's skirts went up or down,stock market performances,baseball World Series wins by an American League team,etc.Thinking about this problem more seriously,you decide to analyze whether or not the presidential candidate for a certain party did better if his party controlled the house.Accordingly you collect data for the last 34 presidential elections.You think of this data as comprising a population which you want to describe,rather than a sample from which you want to infer behavior of a larger population.You generate the accompanying table:
Joint Distribution of Presidential Party Affiliation and Party Control
of House of Representatives,1860-1996
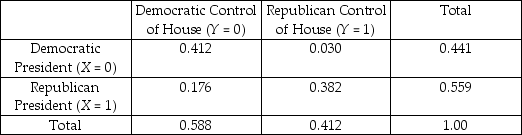 (a)Interpret one of the joint probabilities and one of the marginal probabilities.
(a)Interpret one of the joint probabilities and one of the marginal probabilities.
(b)Compute E(X).How does this differ from E(X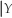 = 0)? Explain.
= 0)? Explain.
(c)If you picked one of the Republican presidents at random,what is the probability that during his term the Democrats had control of the House?
(d)What would the joint distribution look like under independence? Check your results by calculating the two conditional distributions and compare these to the marginal distribution.
Joint Distribution of Presidential Party Affiliation and Party Control
of House of Representatives,1860-1996
 (a)Interpret one of the joint probabilities and one of the marginal probabilities.
(a)Interpret one of the joint probabilities and one of the marginal probabilities.(b)Compute E(X).How does this differ from E(X
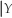 = 0)? Explain.
= 0)? Explain.(c)If you picked one of the Republican presidents at random,what is the probability that during his term the Democrats had control of the House?
(d)What would the joint distribution look like under independence? Check your results by calculating the two conditional distributions and compare these to the marginal distribution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
48
You are at a college of roughly 1,000 students and obtain data from the entire freshman class (250 students)on height and weight during orientation.You consider this to be a population that you want to describe,rather than a sample from which you want to infer general relationships in a larger population.Weight (Y)is measured in pounds and height (X)is measured in inches.You calculate the following sums:  = 94,228.8,
= 94,228.8, 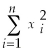 = 1,248.9,
= 1,248.9, 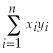 = 7,625.9
= 7,625.9
(small letters refer to deviations from means as in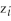 =
= 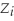 -
- 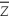 ).
).
(a)Given your general knowledge about human height and weight of a given age,what can you say about the shape of the two distributions?
(b)What is the correlation coefficient between height and weight here?
 = 94,228.8,
= 94,228.8, 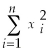 = 1,248.9,
= 1,248.9, 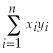 = 7,625.9
= 7,625.9(small letters refer to deviations from means as in
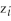 =
= 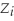 -
- 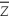 ).
).(a)Given your general knowledge about human height and weight of a given age,what can you say about the shape of the two distributions?
(b)What is the correlation coefficient between height and weight here?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
49
In considering the purchase of a certain stock,you attach the following probabilities to possible changes in the stock price over the next year.
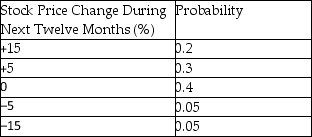 What is the expected value,the variance,and the standard deviation? Which is the most likely outcome? Sketch the cumulative distribution function.
What is the expected value,the variance,and the standard deviation? Which is the most likely outcome? Sketch the cumulative distribution function.
 What is the expected value,the variance,and the standard deviation? Which is the most likely outcome? Sketch the cumulative distribution function.
What is the expected value,the variance,and the standard deviation? Which is the most likely outcome? Sketch the cumulative distribution function.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
50
The accompanying table shows the joint distribution between the change of the unemployment rate in an election year and the share of the candidate of the incumbent party since 1928.You think of this data as a population which you want to describe,rather than a sample from which you want to infer behavior of a larger population.
Joint Distribution of Unemployment Rate Change and Incumbent Party's Vote
Share in Total Vote Cast for the Two Major-Party Candidates,
1928-2000
 (a)Compute and interpret E(Y)and E(X).
(a)Compute and interpret E(Y)and E(X).
(b)Calculate E(Y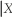 = 1)and E(Y
= 1)and E(Y 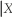 = 0).Did you expect these to be very different?
= 0).Did you expect these to be very different?
(c)What is the probability that the unemployment rate decreases in an election year?
(d)Conditional on the unemployment rate decreasing,what is the probability that an incumbent will lose the election?
(e)What would the joint distribution look like under independence?
Joint Distribution of Unemployment Rate Change and Incumbent Party's Vote
Share in Total Vote Cast for the Two Major-Party Candidates,
1928-2000
 (a)Compute and interpret E(Y)and E(X).
(a)Compute and interpret E(Y)and E(X).(b)Calculate E(Y
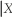 = 1)and E(Y
= 1)and E(Y 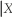 = 0).Did you expect these to be very different?
= 0).Did you expect these to be very different?(c)What is the probability that the unemployment rate decreases in an election year?
(d)Conditional on the unemployment rate decreasing,what is the probability that an incumbent will lose the election?
(e)What would the joint distribution look like under independence?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
51
What would the correlation coefficient be if all observations for the two variables were on a curve described by Y = X2?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
52
Find the following probabilities:
(a)Y is distributed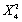 .Find Pr(Y > 9.49).
.Find Pr(Y > 9.49).
(b)Y is distributed t∞.Find Pr(Y > -0.5).
(c)Y is distributed F4,∞.Find Pr(Y < 3.32).
(d)Y is distributed N(500,10000).Find Pr(Y > 696 or Y < 304).
(a)Y is distributed
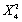 .Find Pr(Y > 9.49).
.Find Pr(Y > 9.49).(b)Y is distributed t∞.Find Pr(Y > -0.5).
(c)Y is distributed F4,∞.Find Pr(Y < 3.32).
(d)Y is distributed N(500,10000).Find Pr(Y > 696 or Y < 304).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
53
Using the fact that the standardized variable Z is a linear transformation of the normally distributed random variable Y,derive the expected value and variance of Z.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
54
You consider visiting Montreal during the break between terms in January.You go to the relevant Web site of the official tourist office to figure out the type of clothes you should take on the trip.The site lists that the average high during January is -7° C,with a standard deviation of 4° C.Unfortunately you are more familiar with Fahrenheit than with Celsius,but find that the two are related by the following linear function: C= 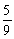 (F - 32).
(F - 32).
Find the mean and standard deviation for the January temperature in Montreal in Fahrenheit.
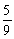 (F - 32).
(F - 32).Find the mean and standard deviation for the January temperature in Montreal in Fahrenheit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
55
Show in a scatterplot what the relationship between two variables X and Y would look like if there was
(a)a strong negative correlation.
(b)a strong positive correlation.
(c)no correlation.
(a)a strong negative correlation.
(b)a strong positive correlation.
(c)no correlation.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
56
Use the definition for the conditional distribution of Y given X = x and the marginal distribution of X to derive the formula for Pr(X = x,Y = y).This is called the multiplication rule.Use it to derive the probability for drawing two aces randomly from a deck of cards (no joker),where you do not replace the card after the first draw.Next,generalizing the multiplication rule and assuming independence,find the probability of having four girls in a family with four children.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
57
Following Alfred Nobel's will,there are five Nobel Prizes awarded each year.These are for outstanding achievements in Chemistry,Physics,Physiology or Medicine,Literature,and Peace.In 1968,the Bank of Sweden added a prize in Economic Sciences in memory of Alfred Nobel.You think of the data as describing a population,rather than a sample from which you want to infer behavior of a larger population.The accompanying table lists the joint probability distribution between recipients in economics and the other five prizes,and the citizenship of the recipients,based on the 1969-2001 period.
Joint Distribution of Nobel Prize Winners in Economics and Non-Economics Disciplines,and Citizenship,1969-2001
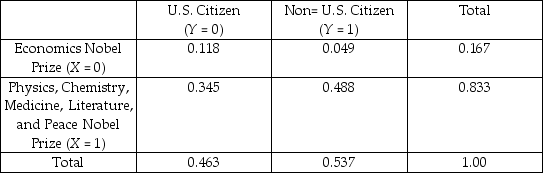 (a)Compute E(Y)and interpret the resulting number.
(a)Compute E(Y)and interpret the resulting number.
(b)Calculate and interpret E(Y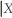 =1)and E(Y
=1)and E(Y 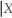 =0).
=0).
(c)A randomly selected Nobel Prize winner reports that he is a non-U.S.citizen.What is the probability that this genius has won the Economics Nobel Prize? A Nobel Prize in the other five disciplines?
(d)Show what the joint distribution would look like if the two categories were independent.
Joint Distribution of Nobel Prize Winners in Economics and Non-Economics Disciplines,and Citizenship,1969-2001
 (a)Compute E(Y)and interpret the resulting number.
(a)Compute E(Y)and interpret the resulting number.(b)Calculate and interpret E(Y
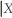 =1)and E(Y
=1)and E(Y 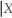 =0).
=0).(c)A randomly selected Nobel Prize winner reports that he is a non-U.S.citizen.What is the probability that this genius has won the Economics Nobel Prize? A Nobel Prize in the other five disciplines?
(d)Show what the joint distribution would look like if the two categories were independent.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
58
The table accompanying lists the joint distribution of unemployment in the United States in 2001 by demographic characteristics (race and gender).
Joint Distribution of Unemployment by Demographic Characteristics,
United States,2001
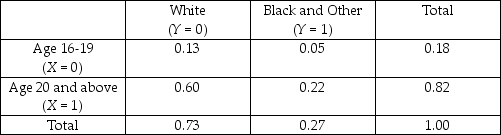 (a)What is the percentage of unemployed white teenagers?
(a)What is the percentage of unemployed white teenagers?
(b)Calculate the conditional distribution for the categories "white" and "black and other."
(c)Given your answer in the previous question,how do you reconcile this fact with the probability to be 60% of finding an unemployed adult white person,and only 22% for the category "black and other."
Joint Distribution of Unemployment by Demographic Characteristics,
United States,2001
 (a)What is the percentage of unemployed white teenagers?
(a)What is the percentage of unemployed white teenagers?(b)Calculate the conditional distribution for the categories "white" and "black and other."
(c)Given your answer in the previous question,how do you reconcile this fact with the probability to be 60% of finding an unemployed adult white person,and only 22% for the category "black and other."

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
59
From the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website the chapter 8 CPS data set (ch8_cps.xls)into a spreadsheet program such as Excel.For the exercise,use the first 500 observations only.Using data for average hourly earnings only (ahe),describe the earnings distribution.Use summary statistics,such as the mean,median,variance,and skewness.Produce a frequency distribution ("histogram")using reasonable earnings class sizes.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
60
The systolic blood pressure of females in their 20s is normally distributed with a mean of 120 with a standard deviation of 9.What is the probability of finding a female with a blood pressure of less than 100? More than 135? Between 105 and 123? You visit the women's soccer team on campus,and find that the average blood pressure of the 25 members is 114.Is it likely that this group of women came from the same population?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
61
SAT scores in Mathematics are normally distributed with a mean of 500 and a standard deviation of 100.The formula for the normal distribution is 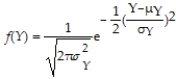 .Use the scatter plot option in a standard spreadsheet program,such as Excel,to plot the Mathematics SAT distribution using this formula.Start by entering 300 as the first SAT score in the first column (the lowest score you can get in the mathematics section as long as you fill in your name correctly),and then increment the scores by 10 until you reach 800.In the second column,use the formula for the normal distribution and calculate f(Y).Then use the scatter plot option,where you eventually remove markers and substitute these with the solid line option.
.Use the scatter plot option in a standard spreadsheet program,such as Excel,to plot the Mathematics SAT distribution using this formula.Start by entering 300 as the first SAT score in the first column (the lowest score you can get in the mathematics section as long as you fill in your name correctly),and then increment the scores by 10 until you reach 800.In the second column,use the formula for the normal distribution and calculate f(Y).Then use the scatter plot option,where you eventually remove markers and substitute these with the solid line option.
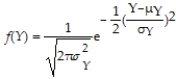 .Use the scatter plot option in a standard spreadsheet program,such as Excel,to plot the Mathematics SAT distribution using this formula.Start by entering 300 as the first SAT score in the first column (the lowest score you can get in the mathematics section as long as you fill in your name correctly),and then increment the scores by 10 until you reach 800.In the second column,use the formula for the normal distribution and calculate f(Y).Then use the scatter plot option,where you eventually remove markers and substitute these with the solid line option.
.Use the scatter plot option in a standard spreadsheet program,such as Excel,to plot the Mathematics SAT distribution using this formula.Start by entering 300 as the first SAT score in the first column (the lowest score you can get in the mathematics section as long as you fill in your name correctly),and then increment the scores by 10 until you reach 800.In the second column,use the formula for the normal distribution and calculate f(Y).Then use the scatter plot option,where you eventually remove markers and substitute these with the solid line option.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
62
The accompanying table gives the outcomes and probability distribution of the number of times a student checks her e-mail daily:
Probability of Checking E-Mail
 Sketch the probability distribution.Next,calculate the c.d.f.for the above table.What is the probability of her checking her e-mail between 1 and 3 times a day? Of checking it more than 3 times a day?
Sketch the probability distribution.Next,calculate the c.d.f.for the above table.What is the probability of her checking her e-mail between 1 and 3 times a day? Of checking it more than 3 times a day?
Probability of Checking E-Mail
 Sketch the probability distribution.Next,calculate the c.d.f.for the above table.What is the probability of her checking her e-mail between 1 and 3 times a day? Of checking it more than 3 times a day?
Sketch the probability distribution.Next,calculate the c.d.f.for the above table.What is the probability of her checking her e-mail between 1 and 3 times a day? Of checking it more than 3 times a day?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
63
The textbook mentioned that the mean of Y,E(Y)is called the first moment of Y,and that the expected value of the square of Y,E(Y2)is called the second moment of Y,and so on.These are also referred to as moments about the origin.A related concept is moments about the mean,which are defined as E[(Y -µY)r].What do you call the second moment about the mean? What do you think the third moment,referred to as "skewness," measures? Do you believe that it would be positive or negative for an earnings distribution? What measure of the third moment around the mean do you get for a normal distribution?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
64
The textbook formula for the variance of the discrete random variable Y is given as 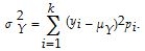 Another commonly used formulation is
Another commonly used formulation is 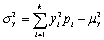 .
.
Prove that the two formulas are the same.
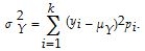 Another commonly used formulation is
Another commonly used formulation is 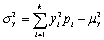 .
.Prove that the two formulas are the same.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
65
Use a standard spreadsheet program,such as Excel,to find the following probabilities from various distributions analyzed in the current chapter:
a.If Y is distributed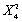 ,find Pr(Y ≤ 7.78)
,find Pr(Y ≤ 7.78)
b.If Y is distributed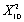 ,find Pr(Y > 18.31)
,find Pr(Y > 18.31)
c.If Y is distributed F10,∞,find Pr(Y > 1.83)
d.If Y is distributed t15,find Pr(Y > 1.75)
e.If Y is distributed t90,find Pr(-1.99 ≤Y ≤ 1.99)
f.If Y is distributed N(0,1),find Pr(-1.99 ≤Y ≤ 1.99)
g.If Y is distributed F10,4,find Pr(Y > 4.12)
h.If Y is distributed F7,120,find Pr(Y > 2.79)
a.If Y is distributed
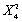 ,find Pr(Y ≤ 7.78)
,find Pr(Y ≤ 7.78)b.If Y is distributed
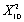 ,find Pr(Y > 18.31)
,find Pr(Y > 18.31)c.If Y is distributed F10,∞,find Pr(Y > 1.83)
d.If Y is distributed t15,find Pr(Y > 1.75)
e.If Y is distributed t90,find Pr(-1.99 ≤Y ≤ 1.99)
f.If Y is distributed N(0,1),find Pr(-1.99 ≤Y ≤ 1.99)
g.If Y is distributed F10,4,find Pr(Y > 4.12)
h.If Y is distributed F7,120,find Pr(Y > 2.79)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
66
Looking at a large CPS data set with over 60,000 observations for the United States and the year 2004,you find that the average number of years of education is approximately 13.6.However,a surprising large number of individuals (approximately 800)have quite a low value for this variable,namely 6 years or less.You decide to drop these observations,since none of your relatives or friends have that few years of education.In addition,you are concerned that if these individuals cannot report the years of education correctly,then the observations on other variables,such as average hourly earnings,can also not be trusted.As a matter of fact you have found several of these to be below minimum wages in your state.Discuss if dropping the observations is reasonable.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
67
Use a standard spreadsheet program,such as Excel,to find the following probabilities from various distributions analyzed in the current chapter:
a.If Y is distributed N (1,4),find Pr(Y ≤ 3)
b.If Y is distributed N (3,9),find Pr(Y > 0)
c.If Y is distributed N (50,25),find Pr(40 ≤ Y ≤ 52)
d.If Y is distributed N (5,2),find Pr(6 ≤ Y ≤ 8)
a.If Y is distributed N (1,4),find Pr(Y ≤ 3)
b.If Y is distributed N (3,9),find Pr(Y > 0)
c.If Y is distributed N (50,25),find Pr(40 ≤ Y ≤ 52)
d.If Y is distributed N (5,2),find Pr(6 ≤ Y ≤ 8)

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
68
Explain why the two probabilities are identical for the standard normal distribution:
Pr(-1.96 ≤ X ≤ 1.96)and Pr(-1.96 < X < 1.96).
Pr(-1.96 ≤ X ≤ 1.96)and Pr(-1.96 < X < 1.96).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
69
The accompanying table lists the outcomes and the cumulative probability distribution for a student renting videos during the week while on campus.
Video Rentals per Week during Semester
 Sketch the probability distribution.Next,calculate the cumulative probability distribution for the above table.What is the probability of the student renting between 2 and 4 a week? Of less than 3 a week?
Sketch the probability distribution.Next,calculate the cumulative probability distribution for the above table.What is the probability of the student renting between 2 and 4 a week? Of less than 3 a week?
Video Rentals per Week during Semester
 Sketch the probability distribution.Next,calculate the cumulative probability distribution for the above table.What is the probability of the student renting between 2 and 4 a week? Of less than 3 a week?
Sketch the probability distribution.Next,calculate the cumulative probability distribution for the above table.What is the probability of the student renting between 2 and 4 a week? Of less than 3 a week?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
70
The Economic Report of the President gives the following age distribution of the United States population for the year 2000:
United States Population By Age Group,2000
 Imagine that every person was assigned a unique number between 1 and 275,372,000 (the total population in 2000).If you generated a random number,what would be the probability that you had drawn someone older than 65 or under 16? Treating the percentages as probabilities,write down the cumulative probability distribution.What is the probability of drawing someone who is 24 years or younger?
Imagine that every person was assigned a unique number between 1 and 275,372,000 (the total population in 2000).If you generated a random number,what would be the probability that you had drawn someone older than 65 or under 16? Treating the percentages as probabilities,write down the cumulative probability distribution.What is the probability of drawing someone who is 24 years or younger?
United States Population By Age Group,2000
 Imagine that every person was assigned a unique number between 1 and 275,372,000 (the total population in 2000).If you generated a random number,what would be the probability that you had drawn someone older than 65 or under 16? Treating the percentages as probabilities,write down the cumulative probability distribution.What is the probability of drawing someone who is 24 years or younger?
Imagine that every person was assigned a unique number between 1 and 275,372,000 (the total population in 2000).If you generated a random number,what would be the probability that you had drawn someone older than 65 or under 16? Treating the percentages as probabilities,write down the cumulative probability distribution.What is the probability of drawing someone who is 24 years or younger?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck
71
Show that the correlation coefficient between Y and X is unaffected if you use a linear transformation in both variables.That is,show that corr(X,Y)= corr(X*,Y*),where X* = a + bX and Y* = c + dY,and where a,b,c,and d are arbitrary non-zero constants.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 71 في هذه المجموعة.
فتح الحزمة
k this deck








