Deck 17: The Theory of Linear Regression With One Regressor
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/49
العب
ملء الشاشة (f)
Deck 17: The Theory of Linear Regression With One Regressor
1
The class of linear conditionally unbiased estimators consists of
A)all estimators of β1 that are linear functions of Y1,…,Yn and that are unbiased,conditional on X1,…,Xn .
B)OLS,WLS,and TSLS.
C)those estimators that are asymptotically normally distributed.
D)all estimators of β1 that are linear functions of X1,…,Xn and that are unbiased,conditional on X1,…,Xn.
A)all estimators of β1 that are linear functions of Y1,…,Yn and that are unbiased,conditional on X1,…,Xn .
B)OLS,WLS,and TSLS.
C)those estimators that are asymptotically normally distributed.
D)all estimators of β1 that are linear functions of X1,…,Xn and that are unbiased,conditional on X1,…,Xn.
A
2
All of the following are good reasons for an applied econometrician to learn some econometric theory,with the exception of
A)turning your statistical software from a "black box" into a flexible toolkit from which you are able to select the right tool for a given job.
B)understanding econometric theory lets you appreciate why these tools work and what assumptions are required for each tool to work properly.
C)learning how to invert a 4×4 matrix by hand.
D)helping you recognize when a tool will not work well in an application and when it is time for you to look for a different econometric approach.
A)turning your statistical software from a "black box" into a flexible toolkit from which you are able to select the right tool for a given job.
B)understanding econometric theory lets you appreciate why these tools work and what assumptions are required for each tool to work properly.
C)learning how to invert a 4×4 matrix by hand.
D)helping you recognize when a tool will not work well in an application and when it is time for you to look for a different econometric approach.
C
3
E 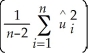
A)is the expected value of the homoskedasticity only standard errors.
B)=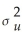 .
.
C)exists only asymptotically.
D)=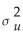 /(n-2).
/(n-2).
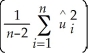
A)is the expected value of the homoskedasticity only standard errors.
B)=
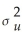 .
.C)exists only asymptotically.
D)=
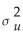 /(n-2).
/(n-2).B
4
Estimation by WLS
A)although harder than OLS,will always produce a smaller variance.
B)does not mean that you should use homoskedasticity-only standard errors on the transformed equation.
C)requires quite a bit of knowledge about the conditional variance function.
D)makes it very hard to interpret the coefficients,since the data is now weighted and not any longer in its original form.
A)although harder than OLS,will always produce a smaller variance.
B)does not mean that you should use homoskedasticity-only standard errors on the transformed equation.
C)requires quite a bit of knowledge about the conditional variance function.
D)makes it very hard to interpret the coefficients,since the data is now weighted and not any longer in its original form.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
5
Slutsky's theorem combines the Law of Large Numbers
A)with continuous functions.
B)and the normal distribution.
C)and the Central Limit Theorem.
D)with conditions for the unbiasedness of an estimator.
A)with continuous functions.
B)and the normal distribution.
C)and the Central Limit Theorem.
D)with conditions for the unbiasedness of an estimator.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
6
The following is not part of the extended least squares assumptions for regression with a single regressor:
A)var(ui Xi)=
Xi)=
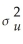 .
.
B)E(ui Xi)= 0.
Xi)= 0.
C)the conditional distribution of ui given Xi is normal.
D)var(ui Xi)=
Xi)=
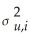 .
.
A)var(ui
 Xi)=
Xi)=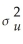 .
.B)E(ui
 Xi)= 0.
Xi)= 0.C)the conditional distribution of ui given Xi is normal.
D)var(ui
 Xi)=
Xi)=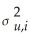 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
7
Besides the Central Limit Theorem,the other cornerstone of asymptotic distribution theory is the
A)normal distribution.
B)OLS estimator.
C)Law of Large Numbers.
D)Slutsky's theorem.
A)normal distribution.
B)OLS estimator.
C)Law of Large Numbers.
D)Slutsky's theorem.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
8
The extended least squares assumptions are of interest,because
A)they will often hold in practice.
B)if they hold,then OLS is consistent.
C)they allow you to study additional theoretical properties of OLS.
D)if they hold,we can no longer calculate confidence intervals.
A)they will often hold in practice.
B)if they hold,then OLS is consistent.
C)they allow you to study additional theoretical properties of OLS.
D)if they hold,we can no longer calculate confidence intervals.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
9
The link between the variance of 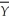 and the probability that
and the probability that 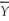 is within (± δ of
is within (± δ of  is provided by
is provided by
A)Slutsky's theorem.
B)the Central Limit Theorem.
C)the Law of Large Numbers.
D)Chebychev's inequality.
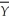 and the probability that
and the probability that 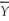 is within (± δ of
is within (± δ of  is provided by
is provided byA)Slutsky's theorem.
B)the Central Limit Theorem.
C)the Law of Large Numbers.
D)Chebychev's inequality.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
10
The following is not one of the Gauss-Markov conditions:
A)var(ui X1,…,Xn)=
X1,…,Xn)=
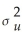 ,0 <
,0 <
 < ∞ for i = 1,…,n,
< ∞ for i = 1,…,n,
B)the errors are normally distributed.
C)E(uiuj X1,…,Xn)= 0,i = 1,…,n,j = 1,... ,n,i ≠ j
X1,…,Xn)= 0,i = 1,…,n,j = 1,... ,n,i ≠ j
D)E(ui X1,…,Xn)= 0
X1,…,Xn)= 0
A)var(ui
 X1,…,Xn)=
X1,…,Xn)=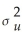 ,0 <
,0 < < ∞ for i = 1,…,n,
< ∞ for i = 1,…,n,B)the errors are normally distributed.
C)E(uiuj
 X1,…,Xn)= 0,i = 1,…,n,j = 1,... ,n,i ≠ j
X1,…,Xn)= 0,i = 1,…,n,j = 1,... ,n,i ≠ jD)E(ui
 X1,…,Xn)= 0
X1,…,Xn)= 0
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
11
You need to adjust 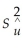 by the degrees of freedom to ensure that
by the degrees of freedom to ensure that  is
is
A)an unbiased estimator of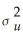 .
.
B)a consistent estimator of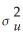 .
.
C)efficient in small samples.
D)F-distributed.
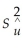 by the degrees of freedom to ensure that
by the degrees of freedom to ensure that  is
isA)an unbiased estimator of
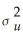 .
.B)a consistent estimator of
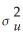 .
.C)efficient in small samples.
D)F-distributed.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
12
When the errors are heteroskedastic,then
A)WLS is efficient in large samples,if the functional form of the heteroskedasticity is known.
B)OLS is biased.
C)OLS is still efficient as long as there is no serial correlation in the error terms.
D)weighted least squares is efficient.
A)WLS is efficient in large samples,if the functional form of the heteroskedasticity is known.
B)OLS is biased.
C)OLS is still efficient as long as there is no serial correlation in the error terms.
D)weighted least squares is efficient.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
13
Finite-sample distributions of the OLS estimator and t-statistics are complicated,unless
A)the regressors are all normally distributed.
B)the regression errors are homoskedastic and normally distributed,conditional on X1,...Xn.
C)the Gauss-Markov Theorem applies.
D)the regressor is also endogenous.
A)the regressors are all normally distributed.
B)the regression errors are homoskedastic and normally distributed,conditional on X1,...Xn.
C)the Gauss-Markov Theorem applies.
D)the regressor is also endogenous.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
14
The Gauss-Markov Theorem proves that
A)the OLS estimator is t distributed.
B)the OLS estimator has the smallest mean square error.
C)the OLS estimator is unbiased.
D)with homoskedastic errors,the OLS estimator has the smallest variance in the class of linear and unbiased estimators,conditional on X1,…,Xn.
A)the OLS estimator is t distributed.
B)the OLS estimator has the smallest mean square error.
C)the OLS estimator is unbiased.
D)with homoskedastic errors,the OLS estimator has the smallest variance in the class of linear and unbiased estimators,conditional on X1,…,Xn.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
15
If,in addition to the least squares assumptions made in the previous chapter on the simple regression model,the errors are homoskedastic,then the OLS estimator is
A)identical to the TSLS estimator.
B)BLUE.
C)inconsistent.
D)different from the OLS estimator in the presence of heteroskedasticity.
A)identical to the TSLS estimator.
B)BLUE.
C)inconsistent.
D)different from the OLS estimator in the presence of heteroskedasticity.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
16
Under the five extended least squares assumptions,the homoskedasticity-only t-distribution in this chapter
A)has a Student t distribution with n-2 degrees of freedom.
B)has a normal distribution.
C)converges in distribution to a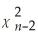 distribution.
distribution.
D)has a Student t distribution with n degrees of freedom.
A)has a Student t distribution with n-2 degrees of freedom.
B)has a normal distribution.
C)converges in distribution to a
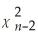 distribution.
distribution.D)has a Student t distribution with n degrees of freedom.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
17
It is possible for an estimator of 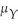 to be inconsistent while
to be inconsistent while
A)converging in probability to .
.
B)Sn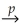
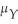 .
.
C)unbiased.
D)Pr → 0.
→ 0.
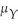 to be inconsistent while
to be inconsistent whileA)converging in probability to
 .
.B)Sn
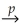
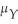 .
.C)unbiased.
D)Pr
 → 0.
→ 0.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
18
Asymptotic distribution theory is
A)not practically relevant,because we never have an infinite number of observations.
B)only of theoretical interest.
C)of interest because it tells you what the distribution approximately looks like in small samples.
D)the distribution of statistics when the sample size is very large.
A)not practically relevant,because we never have an infinite number of observations.
B)only of theoretical interest.
C)of interest because it tells you what the distribution approximately looks like in small samples.
D)the distribution of statistics when the sample size is very large.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
19
The OLS estimator is a linear estimator,  1 =
1 = 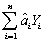 ,where
,where  i =
i =
A)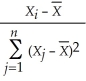 .
.
B) .
.
C)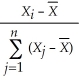 .
.
D) .
.
 1 =
1 = 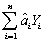 ,where
,where  i =
i =A)
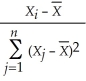 .
.B)
 .
.C)
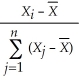 .
.D)
 .
.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
20
If the errors are heteroskedastic,then
A)the OLS estimator is still BLUE as long as the regressors are nonrandom.
B)the usual formula cannot be used for the OLS estimator.
C)your model becomes overidentified.
D)the OLS estimator is not BLUE.
A)the OLS estimator is still BLUE as long as the regressors are nonrandom.
B)the usual formula cannot be used for the OLS estimator.
C)your model becomes overidentified.
D)the OLS estimator is not BLUE.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
21
Assume that the variance depends on a third variable,Wi,which does not appear in the regression function,and that var(ui|Xi,Wi)= θ0+θ1 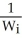 .One way to estimate θ0 and θ1consistently is to regress
.One way to estimate θ0 and θ1consistently is to regress
A) i on
i on
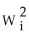 using OLS
using OLS
B) i on
i on
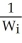 using OLS
using OLS
C)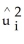 on
on
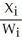 using OLS
using OLS
D)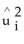 on
on
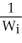 using OLS
using OLS
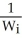 .One way to estimate θ0 and θ1consistently is to regress
.One way to estimate θ0 and θ1consistently is to regressA)
 i on
i on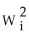 using OLS
using OLSB)
 i on
i on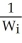 using OLS
using OLSC)
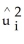 on
on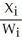 using OLS
using OLSD)
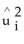 on
on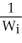 using OLS
using OLS
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
22
If the functional form of the conditional variance function is incorrect,then
A)the standard errors computed by WLS regression routines are invalid
B)the OLS estimator is biased
C)instrumental variable techniques have to be used
D)the regression R2 can no longer be computed
A)the standard errors computed by WLS regression routines are invalid
B)the OLS estimator is biased
C)instrumental variable techniques have to be used
D)the regression R2 can no longer be computed

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
23
Discuss the properties of the OLS estimator when the regression errors are homoskedastic and normally distributed.What can you say about the distribution of the OLS estimator when these features are absent?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
24
(Requires Appendix material)If X and Y are jointly normally distributed and are uncorrelated,
A)then their product is chi-square distributed with n-2 degrees of freedom
B)then they are independently distributed
C)then their ratio is t-distributed
D)none of the above is true
A)then their product is chi-square distributed with n-2 degrees of freedom
B)then they are independently distributed
C)then their ratio is t-distributed
D)none of the above is true

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
25
Homoskedasticity means that
A)var(ui|Xi)=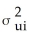
B)var(Xi)=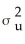
C)var(ui|Xi)=
D)var( i|Xi)=
i|Xi)=
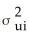
A)var(ui|Xi)=
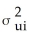
B)var(Xi)=
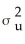
C)var(ui|Xi)=

D)var(
 i|Xi)=
i|Xi)=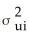

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
26
One of the earlier textbooks in econometrics,first published in 1971,compared "estimation of a parameter to shooting at a target with a rifle.The bull's-eye can be taken to represent the true value of the parameter,the rifle the estimator,and each shot a particular estimate." Use this analogy to discuss small and large sample properties of estimators.How do you think the author approached the n → ∞ condition? (Dependent on your view of the world,feel free to substitute guns with bow and arrow,or missile. )

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
27
In practice,the most difficult aspect of feasible WLS estimation is
A)knowing the functional form of the conditional variance.
B)applying the WLS rather than the OLS formula.
C)finding an econometric package that actually calculates WLS.
D)applying WLS when you have a log-log functional form.
A)knowing the functional form of the conditional variance.
B)applying the WLS rather than the OLS formula.
C)finding an econometric package that actually calculates WLS.
D)applying WLS when you have a log-log functional form.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
28
What does the Gauss-Markov theorem prove? Without giving mathematical details,explain how the proof proceeds.What is its importance?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
29
If the variance of u is quadratic in X,then it can be expressed as
A)var(ui|Xi)=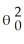
B)var(ui|Xi)= θ0 + θ1
C)var(ui|Xi)= θ0 + θ1
D)var(ui|Xi)=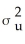
A)var(ui|Xi)=
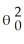
B)var(ui|Xi)= θ0 + θ1

C)var(ui|Xi)= θ0 + θ1

D)var(ui|Xi)=
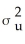

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
30
In practice,you may want to use the OLS estimator instead of the WLS because
A)heteroskedasticity is seldom a realistic problem
B)OLS is easier to calculate
C)heteroskedasticity robust standard errors can be calculated
D)the functional form of the conditional variance function is rarely known
A)heteroskedasticity is seldom a realistic problem
B)OLS is easier to calculate
C)heteroskedasticity robust standard errors can be calculated
D)the functional form of the conditional variance function is rarely known

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
31
"I am an applied econometrician and therefore should not have to deal with econometric theory.There will be others who I leave that to.I am more interested in interpreting the estimation results." Evaluate.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
32
Suppose that the conditional variance is var(ui|Xi)= λh(Xi)where λ is a constant and h is a known function.The WLS estimator is
A)the same as the OLS estimator since the function is known
B)can only be calculated if you have at least 100 observations
C)the estimator obtained by first dividing the dependent variable and regressor by the square root of h and then regressing this modified dependent variable on the modified regressor using OLS
D)the estimator obtained by first dividing the dependent variable and regressor by h and then regressing this modified dependent variable on the modified regressor using OLS
A)the same as the OLS estimator since the function is known
B)can only be calculated if you have at least 100 observations
C)the estimator obtained by first dividing the dependent variable and regressor by the square root of h and then regressing this modified dependent variable on the modified regressor using OLS
D)the estimator obtained by first dividing the dependent variable and regressor by h and then regressing this modified dependent variable on the modified regressor using OLS

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
33
The advantage of using heteroskedasticity-robust standard errors is that
A)they are easier to compute than the homoskedasticity-only standard errors.
B)they produce asymptotically valid inferences even if you do not know the form of the conditional variance function.
C)it makes the OLS estimator BLUE,even in the presence of heteroskedasticity.
D)they do not unnecessarily complicate matters,since in real-world applications,the functional form of the conditional variance can easily be found.
A)they are easier to compute than the homoskedasticity-only standard errors.
B)they produce asymptotically valid inferences even if you do not know the form of the conditional variance function.
C)it makes the OLS estimator BLUE,even in the presence of heteroskedasticity.
D)they do not unnecessarily complicate matters,since in real-world applications,the functional form of the conditional variance can easily be found.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
34
In order to use the t-statistic for hypothesis testing and constructing a 95% confidence interval as  1.96 standard errors,the following three assumptions have to hold:
1.96 standard errors,the following three assumptions have to hold:
A)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;Xi and ui have four moments
B)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;homoskedasticity
C)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;the conditional distribution of ui given Xi is normal
D)none of the above
 1.96 standard errors,the following three assumptions have to hold:
1.96 standard errors,the following three assumptions have to hold:A)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;Xi and ui have four moments
B)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;homoskedasticity
C)the conditional mean of ui,given Xi is zero; (Xi,Yi),i = 1,2,…,n are i.i.d.draws from their joint distribution;the conditional distribution of ui given Xi is normal
D)none of the above

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
35
Consider the model Yi = β1Xi + ui,where ui = c 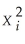 ei and all of the X's and e's are i.i.d.and distributed N(0,1).
ei and all of the X's and e's are i.i.d.and distributed N(0,1).
(a)Which of the Extended Least Squares Assumptions are satisfied here? Prove your assertions.
(b)Would an OLS estimator of β1 be efficient here?
(c)How would you estimate β1 by WLS?
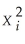 ei and all of the X's and e's are i.i.d.and distributed N(0,1).
ei and all of the X's and e's are i.i.d.and distributed N(0,1).(a)Which of the Extended Least Squares Assumptions are satisfied here? Prove your assertions.
(b)Would an OLS estimator of β1 be efficient here?
(c)How would you estimate β1 by WLS?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
36
Feasible WLS does not rely on the following condition:
A)the conditional variance depends on a variable which does not have to appear in the regression function.
B)estimating the conditional variance function.
C)the key assumptions for OLS estimation have to apply when estimating the conditional variance function.
D)the conditional variance depends on a variable which appears in the regression function.
A)the conditional variance depends on a variable which does not have to appear in the regression function.
B)estimating the conditional variance function.
C)the key assumptions for OLS estimation have to apply when estimating the conditional variance function.
D)the conditional variance depends on a variable which appears in the regression function.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
37
"One should never bother with WLS.Using OLS with robust standard errors gives correct inference,at least asymptotically." True,false,or a bit of both? Explain carefully what the quote means and evaluate it critically.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
38
The WLS estimator is called infeasible WLS estimator when
A)the memory required to compute it on your PC is insufficient.
B)the conditional variance function is not known.
C)the numbers used to compute the estimator get too large.
D)calculating the weights requires you to take a square root of a negative number.
A)the memory required to compute it on your PC is insufficient.
B)the conditional variance function is not known.
C)the numbers used to compute the estimator get too large.
D)calculating the weights requires you to take a square root of a negative number.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
39
The large-sample distribution of 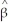 1 is
1 is
A) (
(
 1-β1)
1-β1)
 N(0
N(0
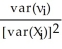 where νi= (Xi-μx)ui
where νi= (Xi-μx)ui
B) (
(
 1-β1)
1-β1)
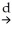 N(0
N(0
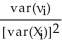 where νi= ui
where νi= ui
C)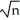 (
(
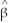 1-β1)
1-β1)
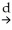 N(0
N(0
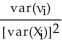 where νi= Xiui
where νi= Xiui
D) (
(
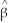 1-β1)
1-β1)
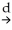 N(0
N(0
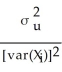
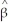 1 is
1 isA)
 (
( 1-β1)
1-β1) N(0
N(0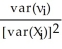 where νi= (Xi-μx)ui
where νi= (Xi-μx)uiB)
 (
( 1-β1)
1-β1) N(0
N(0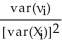 where νi= ui
where νi= uiC)
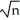 (
(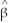 1-β1)
1-β1)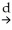 N(0
N(0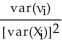 where νi= Xiui
where νi= XiuiD)
 (
(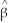 1-β1)
1-β1) N(0
N(0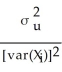

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
40
Assume that var(ui|Xi)= θ0+θ1 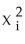 .One way to estimate θ0 and θ1 consistently is to regress
.One way to estimate θ0 and θ1 consistently is to regress
A) i on
i on
 using OLS
using OLS
B) on
on
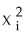 using OLS
using OLS
C)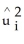 on
on
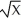 iusing OLS
iusing OLS
D)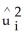 on
on
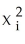 using OLS but suppressing the constant ("restricted least squares")
using OLS but suppressing the constant ("restricted least squares")
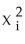 .One way to estimate θ0 and θ1 consistently is to regress
.One way to estimate θ0 and θ1 consistently is to regressA)
 i on
i on using OLS
using OLSB)
 on
on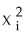 using OLS
using OLSC)
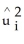 on
on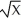 iusing OLS
iusing OLSD)
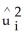 on
on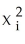 using OLS but suppressing the constant ("restricted least squares")
using OLS but suppressing the constant ("restricted least squares")
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
41
Consider estimating a consumption function from a large cross-section sample of households.Assume that households at lower income levels do not have as much discretion for consumption variation as households with high income levels.After all,if you live below the poverty line,then almost all of your income is spent on necessities,and there is little room to save.On the other hand,if your annual income was $1 million,you could save quite a bit if you were a frugal person,or spend it all,if you prefer.Sketch what the scatterplot between consumption and income would look like in such a situation.What functional form do you think could approximate the conditional variance var(ui  Inome)?
Inome)?
 Inome)?
Inome)?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
42
Consider the model Yi - β1Xi + ui,where the Xi and ui the are mutually independent i.i.d.random variables with finite fourth moment and E(ui)= 0.
(a)Let 1 denote the OLS estimator of β1.Show that
1 denote the OLS estimator of β1.Show that 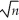 (
( 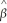 1- β1)=
1- β1)= 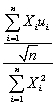 .
.
(b)What is the mean and the variance of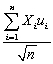 ? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
(c)Deduce the limiting distribution of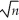 (
( 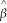 1 - β1)? State what theorems are necessary for your deduction.
1 - β1)? State what theorems are necessary for your deduction.
(a)Let
 1 denote the OLS estimator of β1.Show that
1 denote the OLS estimator of β1.Show that 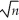 (
( 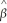 1- β1)=
1- β1)= 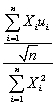 .
.(b)What is the mean and the variance of
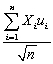 ? Assuming that the Central Limit Theorem holds,what is its limiting distribution?
? Assuming that the Central Limit Theorem holds,what is its limiting distribution?(c)Deduce the limiting distribution of
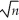 (
( 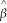 1 - β1)? State what theorems are necessary for your deduction.
1 - β1)? State what theorems are necessary for your deduction.
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
43
(Requires Appendix material)State and prove the Cauchy-Schwarz Inequality.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
44
Consider the simple regression model Yi = β0 + β1Xi + ui where Xi > 0 for all i,and the conditional variance is var(ui  Xi)= θX
Xi)= θX 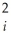 where θ is a known constant with θ > 0.
where θ is a known constant with θ > 0.
(a)Write the weighted regression as i = β0
i = β0 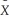 0i + β1
0i + β1 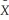 1i +
1i +  i.How would you construct
i.How would you construct  i,
i, 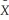 0i and
0i and 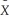 1i?
1i?
(b)Prove that the variance of is i homoskedastic.
i homoskedastic.
(c)Which coefficient is the intercept in the modified regression model? Which is the slope?
(d)When interpreting the regression results,which of the two equations should you use,the original or the modified model?
 Xi)= θX
Xi)= θX 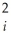 where θ is a known constant with θ > 0.
where θ is a known constant with θ > 0.(a)Write the weighted regression as
 i = β0
i = β0 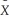 0i + β1
0i + β1 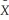 1i +
1i +  i.How would you construct
i.How would you construct  i,
i, 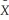 0i and
0i and 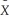 1i?
1i?(b)Prove that the variance of is
 i homoskedastic.
i homoskedastic.(c)Which coefficient is the intercept in the modified regression model? Which is the slope?
(d)When interpreting the regression results,which of the two equations should you use,the original or the modified model?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
45
(Requires Appendix material)If the Gauss-Markov conditions hold,then OLS is BLUE.In addition,assume here that X is nonrandom.Your textbook proves the Gauss-Markov theorem by using the simple regression model Yi = β0 + β1Xi + ui and assuming a linear estimator 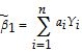 .Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator:
.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 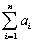 = 0 and
= 0 and 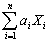 = 1.
= 1.
The variance of the estimator is var(
 X1,…,Xn)=
X1,…,Xn)= 
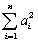 .
.
Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.
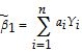 .Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator:
.Substitution of the simple regression model into this expression then results in two conditions for the unbiasedness of the estimator: 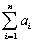 = 0 and
= 0 and 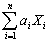 = 1.
= 1.The variance of the estimator is var(

 X1,…,Xn)=
X1,…,Xn)= 
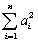 .
.Different from your textbook,use the Lagrangian method to minimize the variance subject to the two constraints.Show that the resulting weights correspond to the OLS weights.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
46
(Requires Appendix material)Your textbook considers various distributions such as the standard normal,t,χ2,and F distribution,and relationships between them.
(a)Using statistical tables,give examples that the following relationship holds: F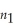 ,∞ =
,∞ = 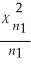 .
.
(b)t∞ is distributed standard normal,and the square of the t-distribution with n2 degrees of freedom equals the value of the F distribution with (1,n2)degrees of freedom.Why does this relationship between the t and F distribution hold?
(a)Using statistical tables,give examples that the following relationship holds: F
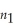 ,∞ =
,∞ = 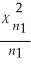 .
.(b)t∞ is distributed standard normal,and the square of the t-distribution with n2 degrees of freedom equals the value of the F distribution with (1,n2)degrees of freedom.Why does this relationship between the t and F distribution hold?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
47
Your textbook states that an implication of the Gauss-Markov theorem is that the sample average, 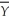 ,is the most efficient linear estimator of E(Yi)when Y1,... ,Yn are i.i.d.with E(Yi)= μY and var(Yi)=
,is the most efficient linear estimator of E(Yi)when Y1,... ,Yn are i.i.d.with E(Yi)= μY and var(Yi)= 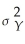 .This follows from the regression model with no slope and the fact that the OLS estimator is BLUE.
.This follows from the regression model with no slope and the fact that the OLS estimator is BLUE.
Provide a proof by assuming a linear estimator in the Y's,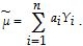 (a)State the condition under which this estimator is unbiased.
(a)State the condition under which this estimator is unbiased.
(b)Derive the variance of this estimator.
(c)Minimize this variance subject to the constraint (condition)derived in (a)and show that the sample mean is BLUE.
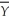 ,is the most efficient linear estimator of E(Yi)when Y1,... ,Yn are i.i.d.with E(Yi)= μY and var(Yi)=
,is the most efficient linear estimator of E(Yi)when Y1,... ,Yn are i.i.d.with E(Yi)= μY and var(Yi)= 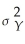 .This follows from the regression model with no slope and the fact that the OLS estimator is BLUE.
.This follows from the regression model with no slope and the fact that the OLS estimator is BLUE.Provide a proof by assuming a linear estimator in the Y's,
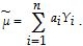 (a)State the condition under which this estimator is unbiased.
(a)State the condition under which this estimator is unbiased.(b)Derive the variance of this estimator.
(c)Minimize this variance subject to the constraint (condition)derived in (a)and show that the sample mean is BLUE.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
48
(Requires Appendix material)This question requires you to work with Chebychev's Inequality.
(a)State Chebychev's Inequality.
(b)Chebychev's Inequality is sometimes stated in the form "The probability that a random variable is further than k standard deviations from its mean is less than 1/k2." Deduce this form.(Hint: choose δ artfully. )
(c)If X is distributed N(0,1),what is the probability that X is two standard deviations from its mean? Three? What is the Chebychev bound for these values?
(d)It is sometimes said that the Chebychev inequality is not "sharp." What does that mean?
(a)State Chebychev's Inequality.
(b)Chebychev's Inequality is sometimes stated in the form "The probability that a random variable is further than k standard deviations from its mean is less than 1/k2." Deduce this form.(Hint: choose δ artfully. )
(c)If X is distributed N(0,1),what is the probability that X is two standard deviations from its mean? Three? What is the Chebychev bound for these values?
(d)It is sometimes said that the Chebychev inequality is not "sharp." What does that mean?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck
49
For this question you may assume that linear combinations of normal variates are themselves normally distributed.Let a,b,and c be non-zero constants.
(a)X and Y are independently distributed as N(a,σ2).What is the distribution of (bX+cY)?
(b)If X1,... ,Xn are distributed i.i.d.as N(a,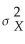 ),what is the distribution of
),what is the distribution of 
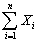 ?
?
(c)Draw this distribution for different values of n.What is the asymptotic distribution of this statistic?
(d)Comment on the relationship between your diagram and the concept of consistency.
(e)Let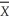 =
= 
 .What is the distribution of
.What is the distribution of  (
( 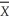 - a)? Does your answer depend on n?
- a)? Does your answer depend on n?
(a)X and Y are independently distributed as N(a,σ2).What is the distribution of (bX+cY)?
(b)If X1,... ,Xn are distributed i.i.d.as N(a,
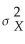 ),what is the distribution of
),what is the distribution of 
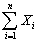 ?
?(c)Draw this distribution for different values of n.What is the asymptotic distribution of this statistic?
(d)Comment on the relationship between your diagram and the concept of consistency.
(e)Let
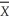 =
= 
 .What is the distribution of
.What is the distribution of  (
( 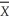 - a)? Does your answer depend on n?
- a)? Does your answer depend on n?
فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 49 في هذه المجموعة.
فتح الحزمة
k this deck








