Deck 3: Linear Programming: Computer Solution and Sensitivity Analysis
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال
سؤال

فتح الحزمة
قم بالتسجيل لفتح البطاقات في هذه المجموعة!
Unlock Deck
Unlock Deck
1/95
العب
ملء الشاشة (f)
Deck 3: Linear Programming: Computer Solution and Sensitivity Analysis
1
Sensitivity analysis determines how a change in a parameter affects the optimal solution.
True
2
Most computer linear programming packages readily accept constraints entered in fractional form, such as X1/X3.
False
3
The sensitivity range for an objective function coefficient is the range of values over which the current optimal solution point (product mix) will remain optimal.
True
4
The marginal value of any scarce resource is the dollar amount one should be willing to pay for one additional unit of that scarce resource.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
5
Sensitivity ranges can be computed only for the right-hand sides of constraints.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
6
The shadow price for a positive decision variable is 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
7
A change in the value of an objective function coefficient will always change the value of the optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
8
When the right-hand sides of two constraints are both increased by one unit, the value of the objective function will be adjusted by the sum of the constraints' prices.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
9
Because the management science model requires that parameters are known with certainty, sensitivity analysis is not used in practical, real-world applications of linear programming.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
10
If we change the constraint quantity to a value outside the sensitivity range for that constraint quantity, the shadow price will change.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
11
The terms shadow price and dual price mean the same thing.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
12
For a profit maximization problem, if the allowable increase for a coefficient in the objective function is infinite, then profits are unbounded.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
13
The sensitivity range for a ________ is the range of values over which the quantity values can change without changing the shadow price.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
14
The sensitivity range for a constraint quantity value is the range over which the shadow price is valid.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
15
The sensitivity range for an objective function coefficient is the range of values over which the profit does not change.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
16
The sensitivity range for a constraint quantity value is the range over which the optimal values of the decision variables do not change.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
17
Sensitivity analysis can be used to determine the effect on the solution for changing several parameters at once.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
18
The simplex method is a graphical technique used to solve all management science problems.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
19
The reduced cost (shadow price) for a positive decision variable is ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
20
The accepted sequence for sensitivity analysis is objective function, left-hand side, and right-hand side.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
21
Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table.
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.
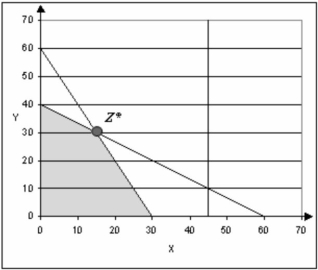
-What is the shadow price for assembly?
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-What is the shadow price for assembly?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
22
The sensitivity range for a constraint quantity value is also the range over which the ________ is valid.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
23
For humanitarian reasons, Taco Loco decides they would rather make product X than product Y. The dollar amount that they can both increase the price of Y and reduce the price of X by to accomplish this reversal of demand is ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
24
Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table.
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-How many tractors and saws should be produced to maximize profit, and how much profit will they make?
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-How many tractors and saws should be produced to maximize profit, and how much profit will they make?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
25
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S):
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-If the company wanted to increase the available hours for one of their constraints (assembly, painting, or inspection) by two hours, they should increase ________.
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-If the company wanted to increase the available hours for one of their constraints (assembly, painting, or inspection) by two hours, they should increase ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
26
Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:
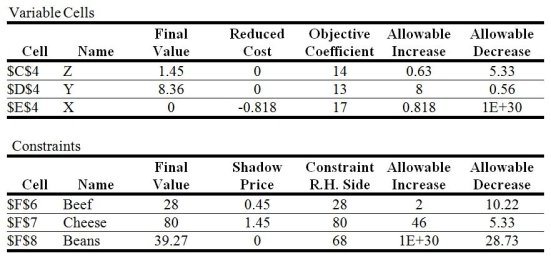
Taco Loco will make the same quantity of X, Y, and Z if the amount of cheese at their disposal is between ________ pounds and ________ pounds.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:

Taco Loco will make the same quantity of X, Y, and Z if the amount of cheese at their disposal is between ________ pounds and ________ pounds.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
27
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S):
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-A change in the market has increased the profit on the super product by $5. Total profit will increase by ________.
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-A change in the market has increased the profit on the super product by $5. Total profit will increase by ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
28
The sensitivity range for a(n) ________ coefficient is the range of values over which the current optimal solution point (product mix) will remain optimal.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
29
Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:

Taco Loco should produce both ________ but should not make any ________.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:

Taco Loco should produce both ________ but should not make any ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
30
________ is the analysis of the effect of parameter changes on the optimal solution.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
31
Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table.
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-What is the shadow price for fabrication?
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-What is the shadow price for fabrication?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
32
What is the maximum amount a manager would be willing to pay for one additional hour of machining time?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
33
A breakdown in fabrication causes the available hours to drop from 120 to 90 hours. How will this impact the optimal number of tractors and mowers produced?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
34
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S):
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-The profit on the super product could increase by ________ without affecting the product mix.
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-The profit on the super product could increase by ________ without affecting the product mix.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
35
Tracksaws, Inc. makes tractors and lawn mowers. The firm makes a profit of $30 on each tractor and $30 on each lawn mower, and they sell all they can produce. The time requirements in the machine shop, fabrication, and tractor assembly are given in the table.
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-Determine the sensitivity range for the profit for tractors.
Formulation:
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
Let x = number of tractors produced per period
y = number of lawn mowers produced per period
MAX 30x + 30y
subject to 2x + y ? 60
2x + 3y ? 120
x ? 45
The graphical solution is shown below.

-Determine the sensitivity range for the profit for tractors.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
36
If Taco Loco reduces the price of the X product by about 82 cents, then their optimal product mix will contain ________ X.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
37
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S):
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-The optimal number of regular products to produce is ________, and the optimal number of super products to produce is ________, for total profits of ________.
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-The optimal number of regular products to produce is ________, and the optimal number of super products to produce is ________, for total profits of ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
38
Taco Loco is considering a new addition to their menu. They have test marketed a number of possibilities and narrowed them down to three new products, X, Y, and Z. Each of these products is made from a different combination of beef, beans, and cheese, and each product has a price point. Taco Loco feels they can sell an X for $17, a Y for $13, and a Z for $14. The company's management science consultant formulates the following linear programming model for company management.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:

Taco Loco should try to purchase additional ________, but should not buy more ________.
Max R = 14Z + 13Y + 17X
subject to:
Beef 2Z + 3Y + 4X ≤ 28
Cheese 9Z + 8Y + 11X ≤ 80
Beans 4Z + 4Y + 2X ≤ 68
X,Y,Z ≥ 0
The sensitivity report from the computer model reads as follows:

Taco Loco should try to purchase additional ________, but should not buy more ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
39
What is the range for the shadow price for assembly?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
40
Consider the following linear program, which maximizes profit for two products--regular (R) and super (S):
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-If downtime reduced the available capacity for painting by 40 hours (from 300 to 260 hours), profits would be reduced by ________.
MAX 50R + 75S
s.t.
1.2 R + 1.6 S ? 600 assembly (hours)
0.8 R + 0.5 S ? 300 paint (hours)
. 16 R + 0.4 S ? 100 inspection (hours)
Sensitivity Report:
-If downtime reduced the available capacity for painting by 40 hours (from 300 to 260 hours), profits would be reduced by ________.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
41
Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. Graphically solve this problem and answer the following questions.
What is the optimal product mix and maximum profit?
What is the optimal product mix and maximum profit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
42
The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles.
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-a) To what value can the per bottle profit on red nail polish drop before the solution (product mix) would change?
b) By how much can the per bottle profit on green nail polish increase before the solution (product mix) would change?
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-a) To what value can the per bottle profit on red nail polish drop before the solution (product mix) would change?
b) By how much can the per bottle profit on green nail polish increase before the solution (product mix) would change?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
43
Max Z = 5x1 + 3x2
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1, x2 ? 0
Determine the sensitivity range for each objective function coefficient.
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1, x2 ? 0
Determine the sensitivity range for each objective function coefficient.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
44
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-if the company decides to increase the amount of syrup it uses during production of these soft drinks to 990 lbs. will the current product mix change? If show what is the impact on profit?
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-if the company decides to increase the amount of syrup it uses during production of these soft drinks to 990 lbs. will the current product mix change? If show what is the impact on profit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
45
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the optimal daily profit?
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the optimal daily profit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
46
For a maximization problem, assume that a constraint is binding. If the original amount of a resource is 4 lbs. and the range of feasibility (sensitivity range) for this constraint is from 3 lbs. to 6 lbs., increasing the amount of this resource by 1 lb. will result in the
A) same product mix, different total profit.
B) different product mix, same total profit as before.
C) same product mix, same total profit.
D) different product mix, different total profit.
A) same product mix, different total profit.
B) different product mix, same total profit as before.
C) same product mix, same total profit.
D) different product mix, different total profit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
47
The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles.
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much space will be left unused? How many minutes of idle time remain for setting up the display?
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-How much space will be left unused? How many minutes of idle time remain for setting up the display?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
48
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the sensitivity range for the per-case profit of a diet soft drink?
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the sensitivity range for the per-case profit of a diet soft drink?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
49
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-How many cases of regular and how many cases of diet soft drink should Whoppy produce to maximize daily profit?
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-How many cases of regular and how many cases of diet soft drink should Whoppy produce to maximize daily profit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
50
The linear programming problem whose output follows is used to determine how many bottles of red nail polish (x1), blue nail polish (x2), green nail polish (x3), and pink nail polish (x4) a beauty salon should stock. The objective function measures profit; it is assumed that every piece stocked will be sold. Constraint 1 measures display space in units, constraint 2 measures time to set up the display in minutes. Note that green nail polish does not require any time to prepare its display. Constraints 3 and 4 are marketing restrictions. Constraint 3 indicates that the maximum demand for red and green polish is 25 bottles, while constraint 4 specifies that the minimum demand for blue, green, and pink nail polish bottles combined is at least 50 bottles.
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-a) By how much can the amount of space decrease before there is a change in the profit?
b) By how much can the amount of space decrease before there is a change in the product mix?
c) By how much can the amount of time available to set up the display can increase before the solution (product mix) would change?
d) What is the lowest value for the amount of time available to set up the display increase before the solution (product mix) would change?
MAX
Subject to 1 .
2.
3.
4.
Optimal Solution:
Objective Function Value = 7475.000
Objective Coefficient Ranges
Right Hand Side Ranges
-a) By how much can the amount of space decrease before there is a change in the profit?
b) By how much can the amount of space decrease before there is a change in the product mix?
c) By how much can the amount of time available to set up the display can increase before the solution (product mix) would change?
d) What is the lowest value for the amount of time available to set up the display increase before the solution (product mix) would change?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
51
Max Z = 5x1 + 3x2
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1, x2 ? 0
Determine the sensitivity range for each constraint.
Subject to: 6x1 + 2x2 ? 18
15x1 + 20x2 ? 60
x1, x2 ? 0
Determine the sensitivity range for each constraint.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
52
The production manager for Beer etc. produces two kinds of beer: light (L) and dark (D). Two resources used to produce beer are malt and wheat. The manager can obtain at most 4800 oz of malt per week and at most 3200 oz of wheat per week, respectively. Each bottle of light beer requires 12 oz of malt and 4 oz of wheat, while a bottle of dark beer uses 8 oz of malt and 8 oz of wheat. Profits for light beer are $2 per bottle, and profits for dark beer are $1 per bottle.
If the production manager decides to produce of 400 bottles of light beer and 0 bottles of dark beer, it will result in slack of
A) malt only.
B) wheat only.
C) both malt and wheat.
D) neither malt nor wheat.
If the production manager decides to produce of 400 bottles of light beer and 0 bottles of dark beer, it will result in slack of
A) malt only.
B) wheat only.
C) both malt and wheat.
D) neither malt nor wheat.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
53
The production manager for Beer etc. produces two kinds of beer: light (L) and dark (D). Two resources used to produce beer are malt and wheat. The manager can obtain at most 4800 oz of malt per week and at most 3200 oz of wheat per week, respectively. Each bottle of light beer requires 12 oz of malt and 4 oz of wheat, while a bottle of dark beer uses 8 oz of malt and 8 oz of wheat. Profits for light beer are $2 per bottle, and profits for dark beer are $1 per bottle.
What is the optimal weekly profit?
A) $1000
B) $900
C) $800
D) $700
What is the optimal weekly profit?
A) $1000
B) $900
C) $800
D) $700

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
54
A plant manager is attempting to determine the production schedule of various products to maximize profit. Assume that a machine hour constraint is binding. If the original amount of machine hours available is 200 minutes., and the range of feasibility is from 130 minutes to 300 minutes, providing two additional machine hours will result in
A) the same product mix, different total profit.
B) a different product mix, same total profit as before.
C) the same product mix, same total profit.
D) a different product mix, different total profit.
A) the same product mix, different total profit.
B) a different product mix, same total profit as before.
C) the same product mix, same total profit.
D) a different product mix, different total profit.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
55
Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. Graphically solve this problem and answer the following questions.
If Mallory Furniture is able to increase the profit per medium shelf to $200, would the company purchase medium shelves? If so, what would be the new product mix and the total profit?
If Mallory Furniture is able to increase the profit per medium shelf to $200, would the company purchase medium shelves? If so, what would be the new product mix and the total profit?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
56
Max Z = 3x1 + 3x2
Subject to : 10x1 + 4x2 ? 60
25x1 + 50x2 ? 200
x1, x2 ? 0
Determine the sensitivity range for each objective function coefficient.
Subject to : 10x1 + 4x2 ? 60
25x1 + 50x2 ? 200
x1, x2 ? 0
Determine the sensitivity range for each objective function coefficient.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
57
The production manager for Beer etc. produces two kinds of beer: light (L) and dark (D). Two resources used to produce beer are malt and wheat. The manager can obtain at most 4800 oz of malt per week and at most 3200 oz of wheat per week, respectively. Each bottle of light beer requires 12 oz of malt and 4 oz of wheat, while a bottle of dark beer uses 8 oz of malt and 8 oz of wheat. Profits for light beer are $2 per bottle, and profits for dark beer are $1 per bottle.
Which of the following is not a feasible solution?
A) 0 L and 0 D
B) 0 L and 400 D
C) 200 L and 300 D
D) 300 L and 200 D
Which of the following is not a feasible solution?
A) 0 L and 0 D
B) 0 L and 400 D
C) 200 L and 300 D
D) 300 L and 200 D

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
58
You are offered the chance to obtain more space. The offer is for 15 units and the total price is $1500. What should you do? Why?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
59
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular (R) and diet (D). The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the sensitivity range of the production time?
The formulation for this problem is given below.
MAX Z = $3R + $2D
s.t.
2R + 4D ? 480
5R + 3D ? 675
The sensitivity report is given below.
Adjustable Cells
Constraints
-What is the sensitivity range of the production time?

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
60
Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. Graphically solve this problem and answer the following questions.
Determine the sensitivity range for the profit on the big shelf.
Determine the sensitivity range for the profit on the big shelf.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
61
What combination of x and y is a feasible solution that minimizes the value of the objective function?
Min Z = 3x + 15y
(1) 2x + 4y ? 12
(2) 5x + 2y ?10
A) x = 0; y = 3
B) x = 0; y = 5
C) x = 5; y = 0
D) x = 6; y = 0
Min Z = 3x + 15y
(1) 2x + 4y ? 12
(2) 5x + 2y ?10
A) x = 0; y = 3
B) x = 0; y = 5
C) x = 5; y = 0
D) x = 6; y = 0

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
62
Given the following linear programming problem:
Max Z = 15x + 20y
S .t.
8x + 5y ? 40
4x + y ? 4
What would be the values of x and y that will maximize revenue?
A) x = 5; y = 0
B) x = 0; y = 8
C) x = 0; y = 1
D) x = 1; y = 0.
Max Z = 15x + 20y
S .t.
8x + 5y ? 40
4x + y ? 4
What would be the values of x and y that will maximize revenue?
A) x = 5; y = 0
B) x = 0; y = 8
C) x = 0; y = 1
D) x = 1; y = 0.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
63
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular and diet. The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
For the production combination of 135 regular cases and 0 diet cases, which resource is completely used up (at capacity)?
A) only time
B) only syrup
C) time and syrup
D) neither time nor syrup
For the production combination of 135 regular cases and 0 diet cases, which resource is completely used up (at capacity)?
A) only time
B) only syrup
C) time and syrup
D) neither time nor syrup

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
64
Given the following linear programming problem that minimizes cost:
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-Determine the optimum values for x and y.
A) x = 2; y = 6
B) x = 6; y = 2
C) x = 12; y = 2
D) x = 6; y = 5
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-Determine the optimum values for x and y.
A) x = 2; y = 6
B) x = 6; y = 2
C) x = 12; y = 2
D) x = 6; y = 5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
65
Given the following linear programming problem that minimizes cost:
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-At the optimal solution, the minimum cost is:
A) $40
B) $50
C) $52
D) $53.33
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-At the optimal solution, the minimum cost is:
A) $40
B) $50
C) $52
D) $53.33

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
66
Given the following linear program that maximizes revenue:
Max Z = 15x + 20y
S )t.
8x + 5y ? 40
4x + y ? 4
What is the maximum revenue at the optimal solution?
A) $120
B) $160
C) $185
D) $200
Max Z = 15x + 20y
S )t.
8x + 5y ? 40
4x + y ? 4
What is the maximum revenue at the optimal solution?
A) $120
B) $160
C) $185
D) $200

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
67
The sensitivity range for the profit on a regular case of soda is
A) $2 to $3.
B) $2 to $4.
C) $1 to $3.
D) $1 to $3.33.
A) $2 to $3.
B) $2 to $4.
C) $1 to $3.
D) $1 to $3.33.

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
68
Which of the following could not be a linear programming problem constraint?
A) A + B ≤ -3
B) A - B ≤ -3
C) A - B ≤ 3
D) -A + B ≤ -3
A) A + B ≤ -3
B) A - B ≤ -3
C) A - B ≤ 3
D) -A + B ≤ -3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
69
For a maximization problem, the shadow price measures the ________ in the value of the optimal solution, per unit increase for a given ________.
A) decrease, resource
B) increase, parameter
C) improvement, resource
D) decrease, parameter
A) decrease, resource
B) increase, parameter
C) improvement, resource
D) decrease, parameter

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
70
The production manager for the Whoppy soft drink company is considering the production of two kinds of soft drinks: regular and diet. The company operates one 8-hour shift per day. Therefore, the production time is 480 minutes per day. During the production process, one of the main ingredients, syrup, is limited to maximum production capacity of 675 gallons per day. Production of a regular case requires 2 minutes and 5 gallons of syrup, while production of a diet case needs 4 minutes and 3 gallons of syrup. Profits for regular soft drink are $3.00 per case and profits for diet soft drink are $2.00 per case.
-Which of the following is not a feasible production combination?
A) 90 R and 75 D
B) 135 R and 0 D
C) 75 R and 90 D
D) 50 R and 50 D
-Which of the following is not a feasible production combination?
A) 90 R and 75 D
B) 135 R and 0 D
C) 75 R and 90 D
D) 50 R and 50 D

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
71
For the constraints given below, which point is in the feasible region of this minimization problem?
(1) 14x + 6y ? 42
(2) x + 3y ? 6
A) x = 2; y = 5
B) x = 1; y = 2
C) x = 2; y = 1
D) x = 2; y = 3
(1) 14x + 6y ? 42
(2) x + 3y ? 6
A) x = 2; y = 5
B) x = 1; y = 2
C) x = 2; y = 1
D) x = 2; y = 3

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
72
Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150.
Which of the following is not a feasible purchase combination?
A) 0 big shelves and 200 medium shelves
B) 0 big shelves and 0 medium shelves
C) 150 big shelves and 0 medium shelves
D) 100 big shelves and 100 medium shelves
Which of the following is not a feasible purchase combination?
A) 0 big shelves and 200 medium shelves
B) 0 big shelves and 0 medium shelves
C) 150 big shelves and 0 medium shelves
D) 100 big shelves and 100 medium shelves

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
73
For a linear programming problem, assume that a given resource has not been fully used. We can conclude that the shadow price associated with that constraint
A) will have a positive value.
B) will have a negative value.
C) will have a value of zero.
D) could have a positive, negative or a value of zero. (no sign restrictions).
A) will have a positive value.
B) will have a negative value.
C) will have a value of zero.
D) could have a positive, negative or a value of zero. (no sign restrictions).

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
74
A shadow price reflects which of the following in a maximization problem?
A) the marginal gain in the objective that would be realized by adding one unit of a resource
B) the marginal gain in the objective that would be realized by subtracting one unit of a resource
C) the marginal cost of adding additional resources
D) the marginal gain of selling one more unit
A) the marginal gain in the objective that would be realized by adding one unit of a resource
B) the marginal gain in the objective that would be realized by subtracting one unit of a resource
C) the marginal cost of adding additional resources
D) the marginal gain of selling one more unit

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
75
For a resource constraint, either its slack value must be ________ or its shadow price must be ________.
A) negative, negative
B) negative, zero
C) zero, zero
D) zero, negative
A) negative, negative
B) negative, zero
C) zero, zero
D) zero, negative

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
76
Mallory Furniture buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $75,000 to invest in shelves this week, and the warehouse has 18,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150.
If the Mallory Furniture company decides to purchase 150 big shelves and no medium shelves, which of the two resources will be left over?
A) investment money only
B) storage space only
C) investment money and storage space
D) neither investment money nor storage space
If the Mallory Furniture company decides to purchase 150 big shelves and no medium shelves, which of the two resources will be left over?
A) investment money only
B) storage space only
C) investment money and storage space
D) neither investment money nor storage space

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
77
Given the following linear programming problem that minimizes cost:
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-What is the sensitivity range for the third constraint, y ? 2?
A) 0 to 4
B) 2 to 5.33
C) 0 to 5.33
D) 4 to 6.33
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-What is the sensitivity range for the third constraint, y ? 2?
A) 0 to 4
B) 2 to 5.33
C) 0 to 5.33
D) 4 to 6.33

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
78
Given the following linear programming problem that minimizes cost:
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-What is the sensitivity range for the cost of x?
A) 0 to 2
B) 4 to 6
C) 2 to 4
D) 0 to 4
Min Z = 2x + 8y
Subject to (1) 8x + 4y ? 64
(2) 2x + 4y ? 32
(3) y ? 2
-What is the sensitivity range for the cost of x?
A) 0 to 2
B) 4 to 6
C) 2 to 4
D) 0 to 4

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
79
Use the constraints given below and determine which of the following points is feasible.
(1) 14x + 6y ? 42
(2) x - y ? 3
A) x = 1; y = 4
B) x = 2; y = 8
C) x = 2; y = 4
D) x = 3; y = 0.5
(1) 14x + 6y ? 42
(2) x - y ? 3
A) x = 1; y = 4
B) x = 2; y = 8
C) x = 2; y = 4
D) x = 3; y = 0.5

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck
80
Sensitivity analysis is the analysis of the effect of ________ changes on the ________.
A) price, company
B) cost, production
C) parameter, optimal solution
D) constraint, parameter
A) price, company
B) cost, production
C) parameter, optimal solution
D) constraint, parameter

فتح الحزمة
افتح القفل للوصول البطاقات البالغ عددها 95 في هذه المجموعة.
فتح الحزمة
k this deck








