A person plans to invest up to $26,000 in two different interest-bearing accounts.Each account is to contain at least $5000.Moreover, the amount in one account should be at least twice the amount in the other account.Find and graph a system of inequalities to describe the various amounts that can be deposited in each account.
A) 
B) 
C) 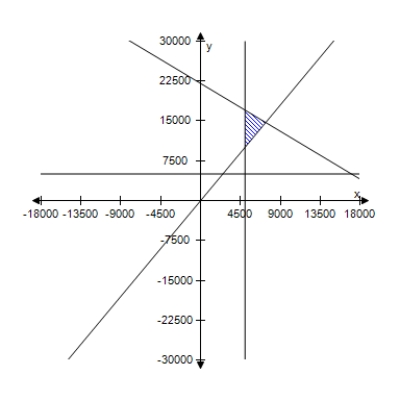
D) 
E) 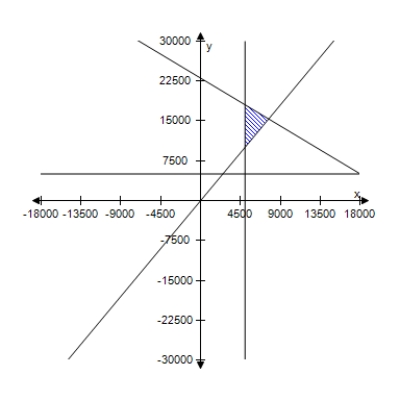
Correct Answer:
Verified
Q83: Sketch the graph and label the
Q84: For the given supply and demand
Q85: Derive a set of inequalities to
Q86: Write an inequality for the shaded
Q87: Use a graphing utility to graph
Q89: Derive a set of inequalities
Q90: Determine which one of the ordered
Q91: Sketch the graph of the inequality.
Q92: For a concert event, there are
Q93: Write the form of the partial
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents