A mathematics class consists of 9 engineering majors E, 14 science majors S, and 8 liberal arts majors LA. What is the probability that a student selected at random will be a science or liberal arts major?
A) Pr(S∪LA) = 
B) Pr(S∪LA) = 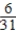
C) Pr(S∪LA) = 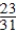
D) Pr(S∪LA) = 
E) Pr(S∪LA) = 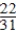
Correct Answer:
Verified
Q52: A bag contains 9 red balls and
Q53: A mathematics class consists of 14 engineering
Q54: A bag contains 4 red balls and
Q55: The following table gives the percent of
Q56: The following table gives the numbers of
Q58: The following table gives the percent of
Q59: The following table gives the percent of
Q60: Of 100 students, 26 can speak French
Q61: A red ball and 19 white balls
Q62: The following table gives the results of
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents