Find the critical point(s) of the function.Then use the second derivative test to classify the nature of each point, if possible.Finally, determine the relative extrema of the function. 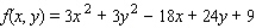
A) (4, 3) ; saddle point: f(4, 3) = 66
B) (- 3, 4) ; relative maximum value: f(- 3, 4) = - 9
C) (3, - 4) ; relative minimum value: f(3, - 4) = - 66
Correct Answer:
Verified
Q120: Find the critical point(s) of the function.Then
Q121: Find the critical point(s) of the function.Then
Q122: Find the critical point(s) of the function.Then
Q123: Find the critical point(s) of the function.Then
Q124: Find the critical point(s) of the function.Then
Q126: Find the critical point(s) of the function.Then
Q127: Find the critical point(s) of the function.Then
Q128: The total daily revenue (in dollars) that
Q129: An auxiliary electric power station will serve
Q130: Find the critical point(s) of the function.Then
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents