Set up the three-dimensional integral where R is the "ice-cream cone" enclosed by a sphere of radius 2 centered at the origin and the cone .Use rectangular coordinates. 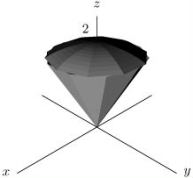
A)
B)
C)
Correct Answer:
Verified
Q21: Set up an iterated integral for
Q22: A cylindrical tube of radius 2cm and
Q23: Set up (but do not evaluate)an
Q24: Compute the area of the flower-like
Q25: Find the triple integral of the
Q27: Consider the volume between a cone centered
Q28: Calculate the following integral:
Q29: Calculate the following integral:
Q30: Suppose a solid is the region
Q31: A solid is bounded below by
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents