For Each Integer $n \geq 3$ , Let $P ( n )$

For each integer $n \geq 3$ , let $P ( n )$ be the equation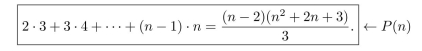

(Recall that by definition $\left. 2 \cdot 3 + 3 \cdot 4 + \cdots + ( n - 1 ) \cdot n = \sum _ { i = 3 } ^ { n } ( i - 1 ) \cdot i . \right)$
(a) Is $P ( 3 )$ true? Justify your answer.
(b) In the inductive step of a proof that $P ( n )$ is true for all integers $n \geq 3$ , we suppose $P ( k )$ is true (this is the inductive hypothesis), and then we show that $P ( k + 1 )$ is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers $k \geq 3$ , if $P ( k )$ is true then $P ( k + 1 )$ is true:
Let $k$ be any integer that is greater than or equal to 3 , and suppose that____ We must show that_____
(c) Finish the proof started in (b) above.